ComputerVision

Reference: Derek Hoiem, Alexei Efros, Steve Seitz, David Forsyth, James Hays, Bob Collins우리가 보고 있는 세계는 연속적인 세계다. 그러나 카메라로 이러한 연속적인 세상을 촬영하는 순간, 3차원의 세

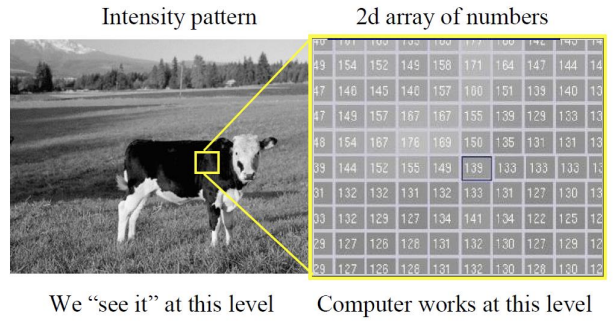
좌측 image는 우리가 실제로 보는 level이다. Computer는 우측 그림과 같이 2d array 형태로 이산화된 level로 동작한다. 3D to 2D projection이 이루어지며 우측 그림과 같이 디지털화되는데, 각 픽셀 하나하나가 포함할 수 있는 영역이

Gaussian Smoothing at Different ScalesQ. Do we have to apply two linear operations here(convolution)?convolution operator의 associativity 속성을 이용해 filte

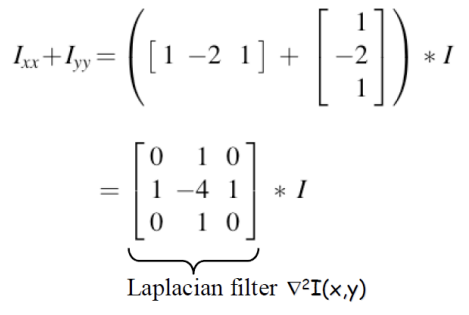
Second-Derivate Filters idea: F(x)의 변곡점을 찾기 위해, 미분을 두 번해서 그 point를 찾고자 한다. F(x)에서 변곡점은 F''(x)에서의 zero-crossing과 대응된다. 장점 2차 미분해서 1차 미분의 maximum을 찾을

stereo와 motion 추정과 같은 vision task는 두 개 이상의 view로부터 correspondence features를 찾아야 한다.코너를 찾으면?1) object의 형상/구조를 알 수 있음.2) 같은 객체를 가지고 correspondence point

Object of Interest in World Coordinate System (U, V, W)Camera Coordinate System (X, Y, Z)f is focal lengthForward Projection onto image plane 3D (X, Y

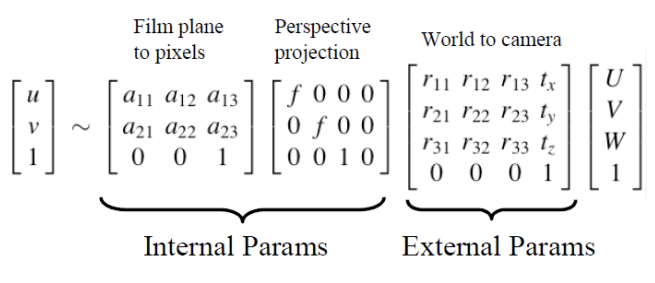
given (u, v). 왜 =이 아니라 ~인가?projection 과정에서 발생하는 loss 때문에 size 정보를 정확히 담지 못해 proportional하기 때문이다.카메라가 2대 이상이라면, 그 카메라 2대로 동시에 어떤 대상을 찍었을 때, depth 정보를

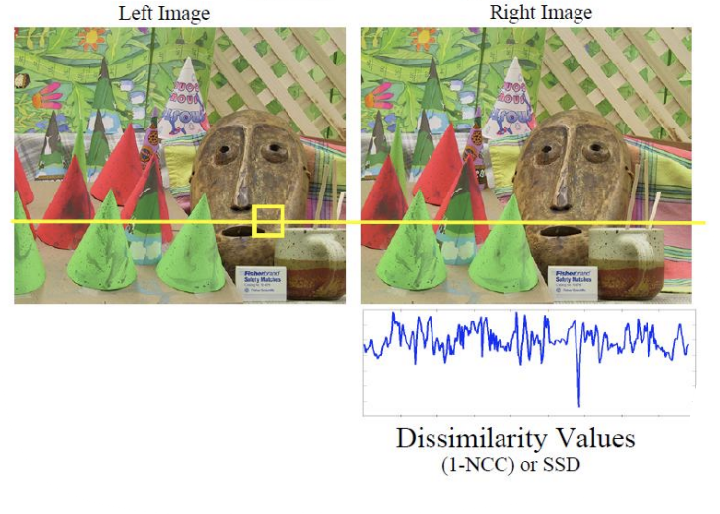
여전히 correspondence problem은 남아있다. 아래와 같은 경우 correspondence matching point를 찾기 어렵다. flat한 영역 전반사(분산이 큰 surface) uniform 반사 (Lambertian surface) 따라서 위 경

Geometric Image Mappings given 2 images 2개의 이미지 사이에 어떤 transformation이 일어났을까? → correspondence point를 찾고, SPARSE한 각각의 point를 가지고 매핑 관계를 알아내자. Linear