Second-Derivate Filters
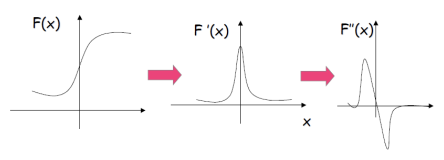
idea: F(x)의 변곡점을 찾기 위해, 미분을 두 번해서 그 point를 찾고자 한다. F(x)에서 변곡점은 F''(x)에서의 zero-crossing과 대응된다.
위 그림은 continuous한 값이다. 하지만 우리가 가지는 image는 discrete하다. 이 때에는 128보다 작고, 128보다 큰 지점이 cross되는 지점을 찾는다.
장점
- 2차 미분해서 1차 미분의 maximum을 찾을 수 있으므로 thresholding할 필요 없다.
- 극댓값은 픽셀 하나이므로 thinning할 필요 없다.
단점 - 미분에 의해 noise가 심해진다.
- 상대적으로 gradient가 작은 곳이 무시된다.
Numerical Derivates

2차 미분에 근사화하는 식이다. 결과적으로 현재 위치값과 왼쪽&오른쪽 값이 필요한 것을 알 수 있다.
Central difference approx to second derivate
위 이미지를 자세히 보면 edge가 '흰->검' 이거나 '검->흰'인 것을 확인할 수 있다.
Edge Detection (1D to 2D)
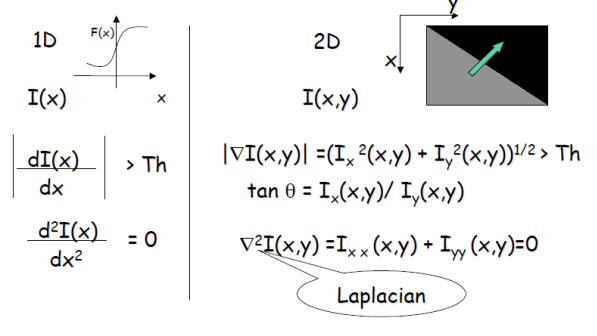
- |∇I| : amplitude (= edgeness, magnitude...)
- tanθ : orientation
- ∇^2I(x,y) = 0
Laplacian: 사실상 정확히 0이 나올 수 없음. (conceptual한 내용임)
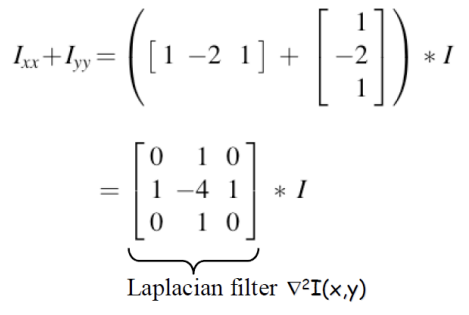
Finite Difference Laplacian
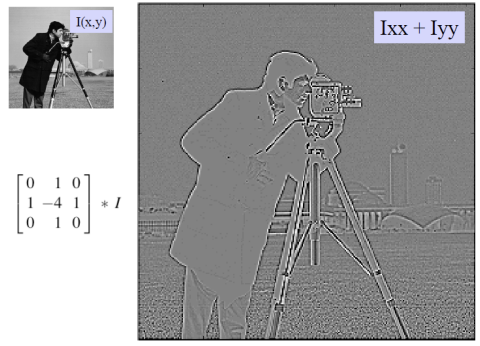
- Example
Notes about the Laplacian
- ∇^2I(x,y) is a Scalar.
* orientation 정보를 잃게 됨. - 미분을 취하는 것은 noise를 더욱 심하게 함.
- 항상 smoothing 연산과 함께 이루어져야 함.
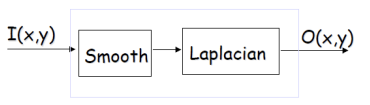
LoG Filter
- First Smooth(Gaussian filter)
- Then, find zero-crossing(Laplacian filter):
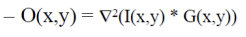
Just anther linear filter
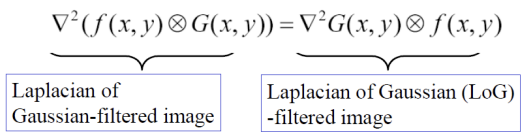
결국에, image에 gaussian filter 통과시킨 것을 laplacian하든, laplacian한 Gaussian filter를 image에 통과시키든 결과는 동일함.
1D Gaussian and Derivates
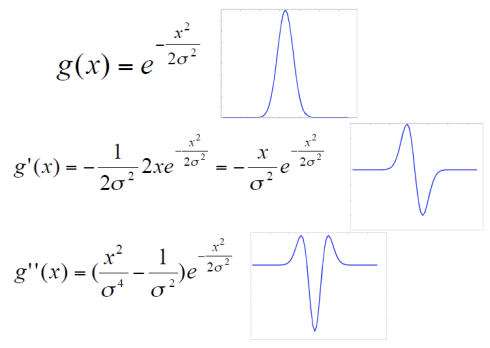
위 그림에서 최하단에 있는 그래프가 LoG filter임.
Second Derivate of a Gaussian
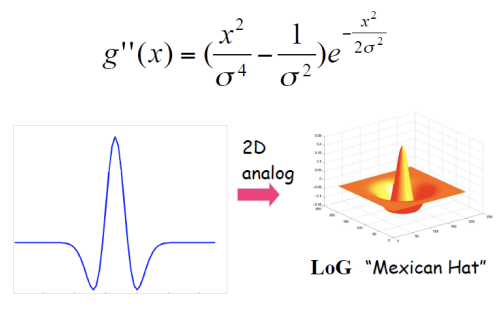
1. 1차 미분
2. 2차 미분
3. 2D analog
4. 얘를 이미지와 convoloution
→ 위 과정을 수행하면 smoothing과 filtering한 결과가 나옴.
Efficient Implementation Approximating LoG with DoG
LoG can be approximated by a Difference of two Gaussians(DoG) at different scales
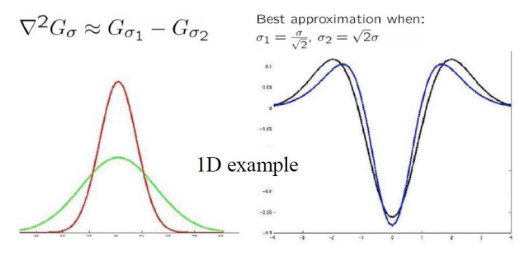
서로 다른 standard를 가지는 Gaussian Filter를 빼주면 LoG에 근사화할 수 있음.
위 그림과 같이 gaussian은 low-pass smoothing이기 때문에 서로 다른 standard를 가진 두 gaussian을 빼줌으로써 LoG에 근사화할 수 있다.
low-pass smoothing(filtering) : high frequency 제거
Efficient Implementation
LoG can be approximate by a Difference of two Gaussians(DoG) at different scales.
Separability of and cascadability of Gaussian applies to the DoG, so we can achieve efficient implementation of the LoG operator.
DoG approx also explains bandpass filtering of LoG
(Think about it. Gaussian is a low-pass filter)
band-pass filter(대역필터): 특정 주파수 사이의 신호만 통과시킴
low-pass filter: 특정한 차단 주파수 이하의 신호만 통과시킴.
- maxima: 흰색
- minima: 검은색
중앙 하단 쪽의 검은색 원을 보자. 이와 같이 주변 픽셀들과 다르게 isolated된 point를 blob이라고 한다. 이러한 blob은 매우 중요한 요소가 될 수 있다.
저번에, filtering을 한다는 것은 커널의 모양과 유사한 point를 찾는 것고 같다고 했다. 그러고보니 LoG filter
(difference of two Gaussian)는 blob 모양이었다. 아 그렇다면 blob detection에 이 필터를 사용할 수 있겠다!
LoG Blob Filtering
LoG filter extema locates "blobs"
- maxima = dark blobs on light background
- minima = light blobs on dark background
Scale of blob(size) is determined by the sigma parameter of the LoG filter

커널 크기를 조절해서 자신이 찾고 싶은 blob(얼굴, 몸통 ...)을 찾을 수 있도록 sigma 2개를 적절히 설정
Observe and Generalize

💡filter로 convolution을 한다는 것은, 네가 찾고 싶은 일종의 "picture"로 이미지에 그와 유사한 영역을 비교하는 것과 같다.
feature detection의 시작
template matching
template matching이라는 개념이 등장한다. 내가 찾고 싶은 영역을 filter로 사용해 detection하자! → 완전 원시적인 수준의 detection
- 이동(translation)에 대해서는 해결 가능 (translation에 robust)
- 회전 및 크기 변화된 이미지에 대해서는 사용 어려움 (rotation, scaling에 sensitive)
Corner Detection
What are Corners?

- corner : 어떤 임의의 픽셀을 기준으로 어떤 방향으로 움직이든 변화를 인지할 수 있다면 corner라고 한다.
- edge : edge 방향 이외의 다른 방향으로 움직이면 변화를 인지할 수 있다. edge 방향으로 움직이면 변화 인지X
- flat : 어떤 방향으로 움직이든 변화를 인지하지 못한다.
그림에서 지붕 끝을 보면 저 곳은 corner가 아니라 edge이다. 그러나 이는 3차원 상에서 corner가 아님에 유의해야 한다. 2차원 상에서는 corner이다.
Motivation For Corner Finding
두 개 이상의 시점에서 촬영한 이미지 사이의 일치하는 feature를 찾는다.
→ 가장 찾기 쉬운 지점이 corner이기 때문에 corner부터 correspondence matching할 것임.
방법 1) robust(하나씩 인간이 point를 찍음) → 명시적으로 문제 해결 X
방법 2) template matching → 명시적으로 문제 해결
그렇다면 이 corner를 찾아서 어디에 쓰지?
1) 이미지 속 object의 배치와 구조를 알 수 있다.
2) 같은 object를 가지고 correspondence point(pair가 되는 point)를 찾을 수 있고, 이를 통해 3차원 정보를 추정해낼 수 있다.
correspondence point를 많이 찾을수록 depth 정보가 많이 생기기 때문
Harris Corner Detector
Harris Corner Detecotr: Basic Idea
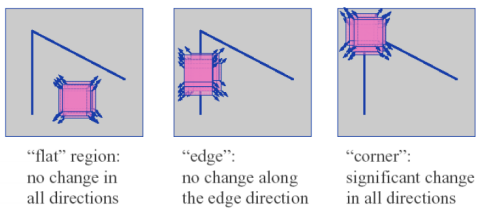
- flat한 영역은 정해진 영역(patch)을 어느 방향으로 이동시켜도 변화를 인지하기 어려움.
- edge는 edge 방향으로 이동시키면 변화를 인지하기 어려움.
- corner는 어느 방향으로 이동시켜도 변화를 확실히 인지할 수 있음.
Harris Detector: Mathematics
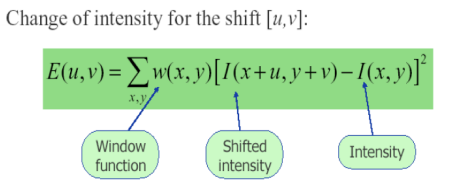
- I(x,y) : Intensity (original patch)
- I(x+u,y+v) : shifted intensity (shifted patch)
- w(x,y) : window function
- E(u,v) : 두 patch 사이의 dissimilarity를 계산
- 값이 크면 corner일 확률 ↑
- 값이 작으면 flat할 확률 ↑
Taylor Series for 2D Functions

매번 shift시켜서 계산하는 것보다 현재 위치를 이용해 계산하는 것이 계산상 편리하므로 Taylor Series로 approximation하겠다!
Harris Corner Derivation
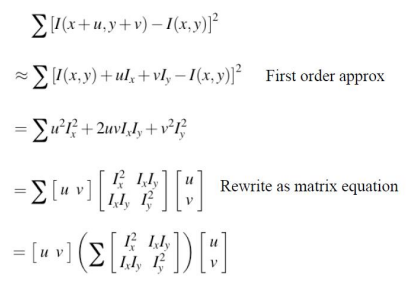
가장 아래 식을 보자.
- u와 v는 shift이다.
- 이 행렬은 이미지에서 도출되는 값이므로, 결국 이 계산에 있어서 input은 'shift를 얼마로 해야할지'가 됨.
Harris Detector: Mathematics

u와 v는 우리가 shift를 try해보는 값이다.
결국, corner인지 edge인지의 특징을 가지고 있는 것은 M이다. M이 우리가 원하는 정보를 가지고 있는 matrix이다.
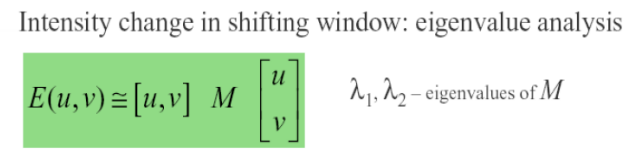
- 결국에, M이 의미있는 값이라면, 이 M matrix는 full rank일 것임.
- full rank라는 것은 2개의 eigenvalue가 의미있는 값이라는 의미이다.
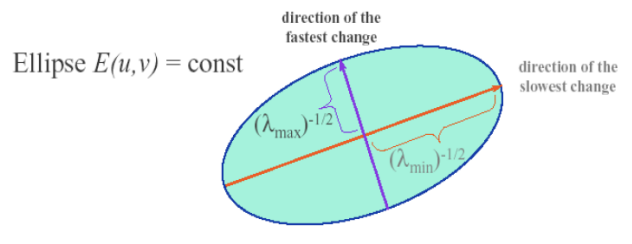
→ 각 eigenvalue값은 주어진 방향으로 얼마나 빠르게 변하는지에 대한 정보를 담고 있음.
Classification via Eigenvalues
M matrix의 eigenvalues 값들을 이용해 image points를 분류해보자.
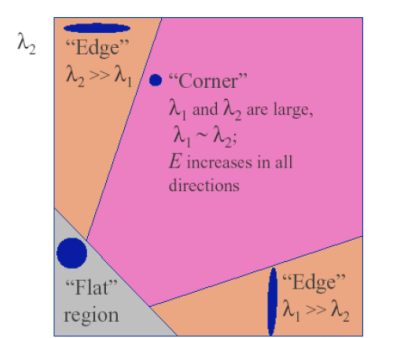
- eigenvalue 2개가 모두 작으면 E는 모든 방향으로 거의 일정하다.
flat - eigenvalue 둘 중 하나가 나머지보다 크면 한 쪽 방향으로만 변화가 크다.
edge - eigenvalue 2개가 모두 값이 크면 두 방향으로 전부 변화가 크다.
corner
요약
- F(x)의 변곡점이 바로 gradient가 크게 변하는 point이다. 따라서 변곡점을 찾고자 2차 미분을 하고자 했다.
- 그러나 미분은 noise를 증폭시킬 뿐더러 연산량이 매우 커진다. 따라서 Laplacian으로 approximation을 하려 했고, 이로써 Laplacian filter를 도출해냈다.
- smoothing 후에 derivate를 구한다. 그런데 이 때, gaussian filter로 convolution한 뒤에 laplacian을 하든, gaussian filter에 laplacian을 한 뒤, 이미지에 convolution하든 결과는 동일하다.
- 따라서 우리는 Laplacian of Gaussian Filter를 사용하기로 하고, 이를 이미지에 convolution한다.
- LoG를 통과시킨 이미지 또한, LoG filter와 유사한 형태의 blob이 detection되었다.
filter로 convolution을 한다는 것은, 네가 찾고 싶은 "picture"로 image에 그와 유사한 영역을 비교하는 것과 같다. - 이렇게 feature detection이 시작되었는데, 우리는 여기서 template matching을 배웠다. template matching은 translation에 robust하고, rotation 또는 scaling에는 취약하다.
- 시점이 다른 두 이미지 사이에 correspondence matching을 해보자.
- flat한 영역은 어떤 방향으로 이동시키든 변화를 인지할 수 없고, edge는 edge 방향으로 이동시키면 변화를 인지할 수 없고, corner는 어떤 방향으로 이동시키든 변화를 인지할 수 있다. 따라서 우리는 correspondence 문제에 있어 corner를 먼저 detection하고자 한다.
- image의 intensity를 u, v 방향으로 shift하며 dissimilarity를 계산한다. 이 dissimilarity는 클수록 corner일 확률이 높아지고, 작을수록 flat할 확률이 높아진다.
- shift시키며 계산하는 것은 번거로우니, Taylor Series로 Approximation하겠다. approximation된 것을 바탕으로 식을 정리해주니, 결국에 유의미한 정보는 전부 M matrix가 저장하고 있다는 것을 알게된다.
- M matrix의 eigenvalue를 구해, 두 값의 크기를 비교해 flat한지, edge인지, corner인지를 판별할 수 있다.