CH 04. 분류

01. 분류의 개요

• 지도학습은 명시적인 정답이 있는 데이터가 주어지 상태에서 학습하는 머신러닝 방식이다.
• 분류는 지도학습의 대표적인 유형이다. : 학습 데이터로 주어진 데이터의 피처와 레이블값을 머신러닝 알고리즘으로 학습해 모델링하고, 그 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측한다.

1. 분류의 종류

1. 나이브 베이즈 : 베이즈 통계와 생성 모델에 기반
2. 로지스틱 회귀: 독립변수와 종속변수의 선형 관계성에 기반
3. 결정 트리 : 데이터 균일도에 따른 규칙 기반
4. 서포트 벡터 머신 : 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아줌
5. 최소근접 알고리즘 : 근접 거리 기준
6. 신경망: 심층 연결 기반
7. 앙상블 : 서로 같거나 다른 머신러닝 알고리즘을 결합

02. 결정 트리

1. 결정트리 개요

• 데이터에 있는 규칙을 학습을 통해 트리 기반의 분류 규칙을 만든다.
• 일반적으로 if/else 기반으로 나타내는데 스무고개 게임처럼 if/else를 반복하며 분류
• 장점
  1. 균일도를 기반으로 하기 때문에 쉽고 직관적이다.
  2. 룰이 매우 명확하여 규칙노드와 리프 노드가 만들어지는 기준을 파악할 수 있다
• 정보의 균일도만 신경쓰면 되기 때문에 사적 가공이 많이 필요하지 않다
• 단점
  1. 과적합으로 알고리즘 성능이 떨어질 수 있다. à 피처가 많고 균일도가 다양하게 존재할수록 트리의 깊이가 커지고 복잡해질 수 밖에 없다. (학습 데이터를 기반으로 정확도를 올리기 위해 계속 조건을 추가하기 때문에 깊이가 깊어지고 복잡한 모델이되어 새로운 상황에 대한 예측력이 떨어진다.)
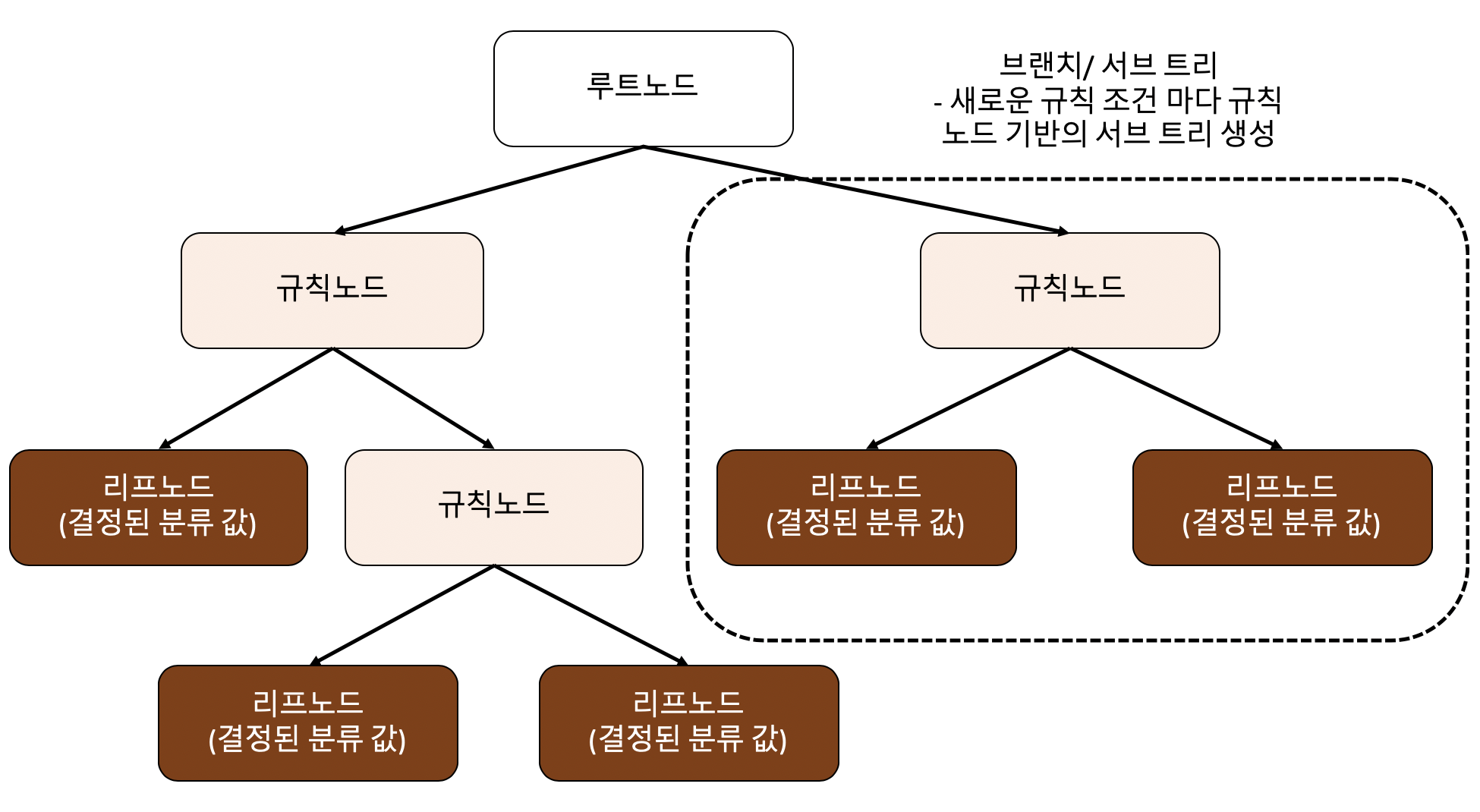
• 결정 트리 구조
  • 루트노드 : 트리 구조가 시작되는 곳
  • 규칙노드 : 규칙조건이 되는 것
  • 리프노드 : 결정된 클래스 값 (더 이상 자식 노드가 없는 것)
  • 서브트리 : 새로운 규칙 조건마다 생성
    
• 규칙의 기준은 순수도를 가장 높여줄 수 있는 쪽을 선택해 진행한다. – 최대한 균일한 데이터 세트를 구성할 수 있도록 분할하는 것이 필요
• 그림에서 균일한 데이터 세트의 순서는 1 = 2 > 3 이다.

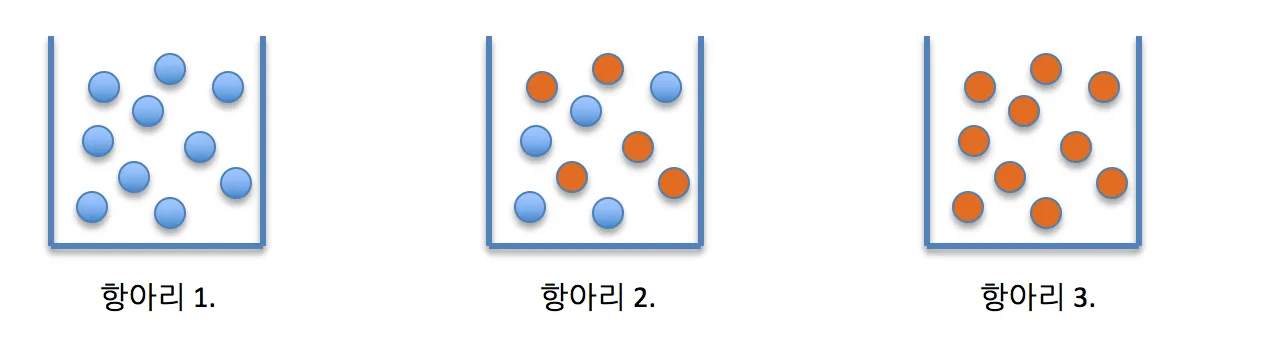
항아리에 10개의 구슬이 들어 있고 그 중 절반가량이 빨간색이고 나머지 절반가량이 파란색인 경우 그 구슬들의 집합은 빨간색과 파란색이 섞여 있어 불순한 것으로 간주한다 (항아리 2). 반면에 항아리에 빨간색 또는 파란색 구슬만 있는 경우 그 구슬 집합은 완벽하게 순수한 것으로 간주한다.

결정노드는 정보 균일도가 높은 데이터를 먼저 선택하도록 규칙을 만든다. 즉 데이터를 나눌 수 있는 조건을 찾아 자식 노드를 만들며 내려가게 된다. 이때 정보의 균일도를 측정하는 대표적인 방법은 엔트로피를 이용한 정보 이득 지수와 지니계수가 있다.

• 엔트로피, 정보이득지수, 지니 계수
  • 엔트로피 : 주어진 데이터 집합의 혼잡도 (<->균일도) (값이 작을수록 데이터가 균일)
  • 정보이득지수 : 1- 엔트로피 지수 (정보 이득이 높은 속성을 기준으로 분할)
  • 지니계수: 0이 가장 평등하고 1로 갈수록 불평등하다. (지니 계수가 낮을수록 데이터 균일도가 높다 à 지니계수가 낮은 속성을 기준으로 분할)

2. 결정트리 파라미터

• min_samples_split
  - 노드를 분할하기 위한 최소한의 샘플 데이터 수
  - 과적합 제어 용도
  - 디폴트 2 (작게 설정할수록 과적합 가능성 증가)
• min_samples_leaf
  - 말단 노드가 되기 위한 최소한의 샘플 데이터 수
  - 과적합 제어 용도
  - 비대칭적 데이터(하나의 피처가 과도하게 많은 경우) 에는 특정 클래스의 데이터가 극도로 작을 수 있으므로 작게 설정
  - 말단 노드의 최대 개수
• max_features
  - 최적의 분할을 위해 고려할 최대 피처 개수
  - 디폴트 = none (데이터 세트의 모든 피처를 사용해 분할)
  - max_features = sqrt/ auto : √(전체 피처 개수)
  - max_features = log2 : log2(피처 개수)
  - Int형으로 지정하면 대상 피처의 개수, float형으로 지정하면 전체 피처 중 대상 피처의 퍼센트
• max _depth
  - 트리의 최대 깊이
  - 디폴트 = None (완벽하게 클래스 결정값이 될 때까지 깊이를 계속 키우며 분할 하거나 노드가 가지는 데이터의 개수가 min_sample_split보다 작아질때까지 계속 깊이를증가 시킨다.)
  - 깊이가 깊어지면 과적합하므로 주의

3. 결정 트리 모델의 시각화

결정트리는 Graphviz 패키지 이용하여 시각화 할 수 있다.

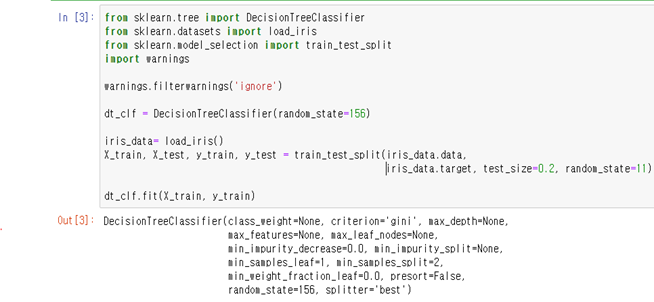
test_size = test데이터의 비율

random_state = 난수 값 고정

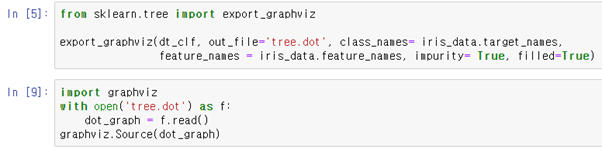
Impurity가 True일 경우 각 노드의 불순물을 표시한다.

filled는 True일 경우 분류를 위한 다수 클래스, 회귀 값의 극한 또는 다중 출력의 노드 순도를 나타내기 위해 노드를 색칠한다.

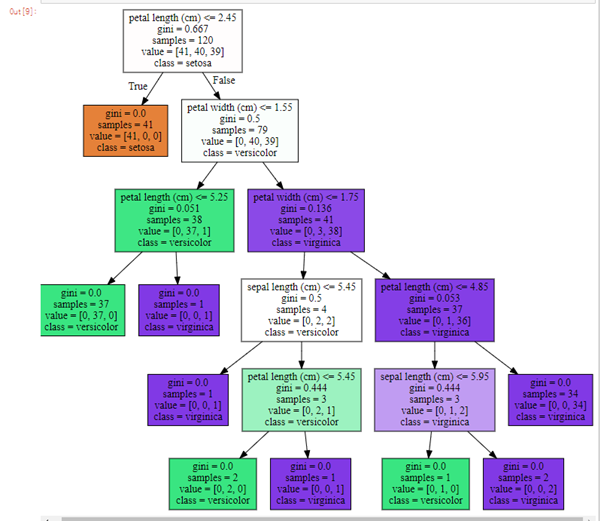
graphviz를 이용한 결정트리 시각화

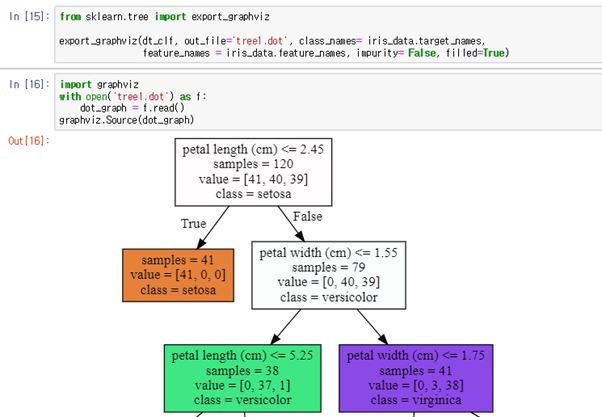
두 그림을 비교해보면 impurity=False일때 gini 계수가 사라진 것을 알 수 있다.

4. Graphviz로 시각화된 결정 트리 지표 설명

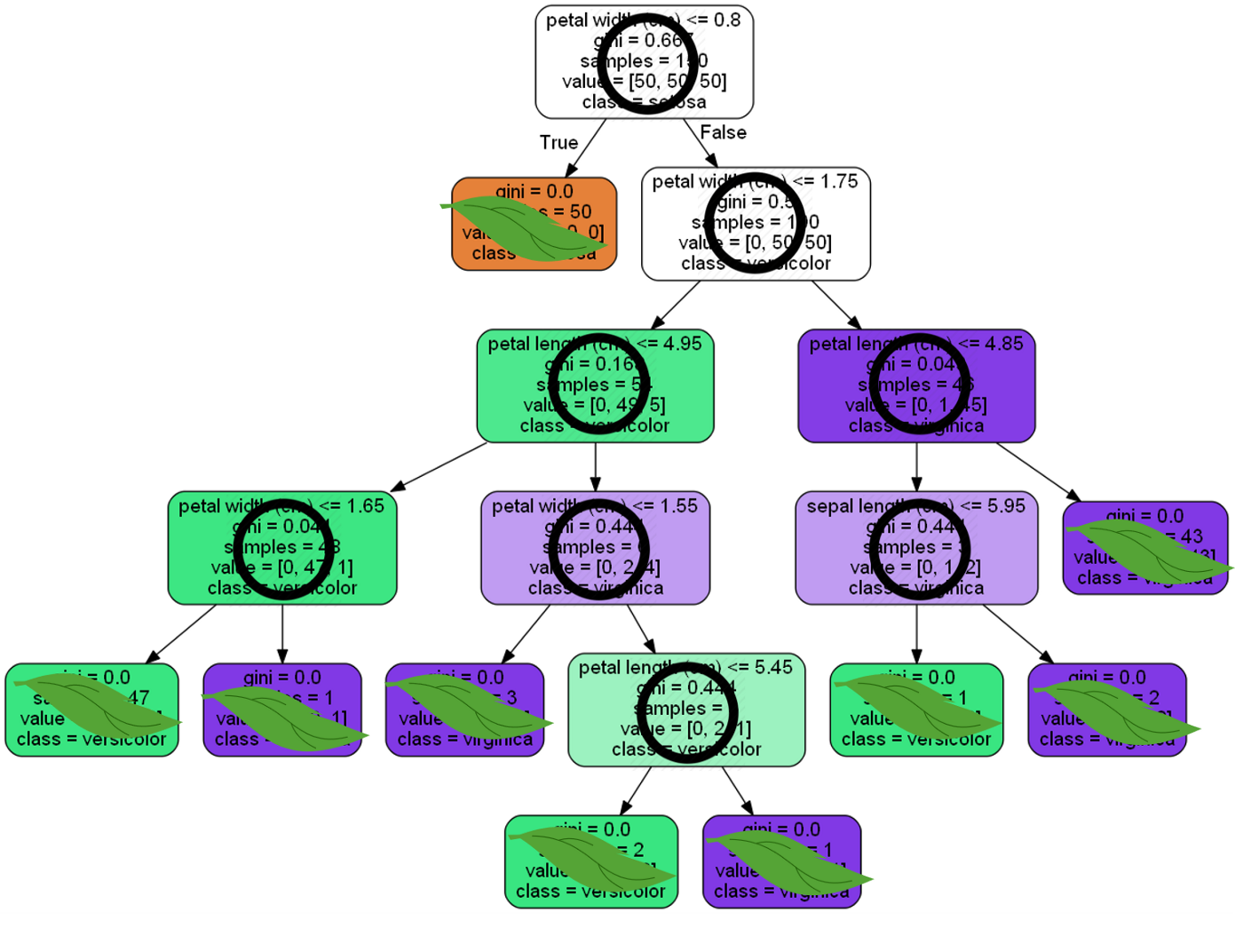
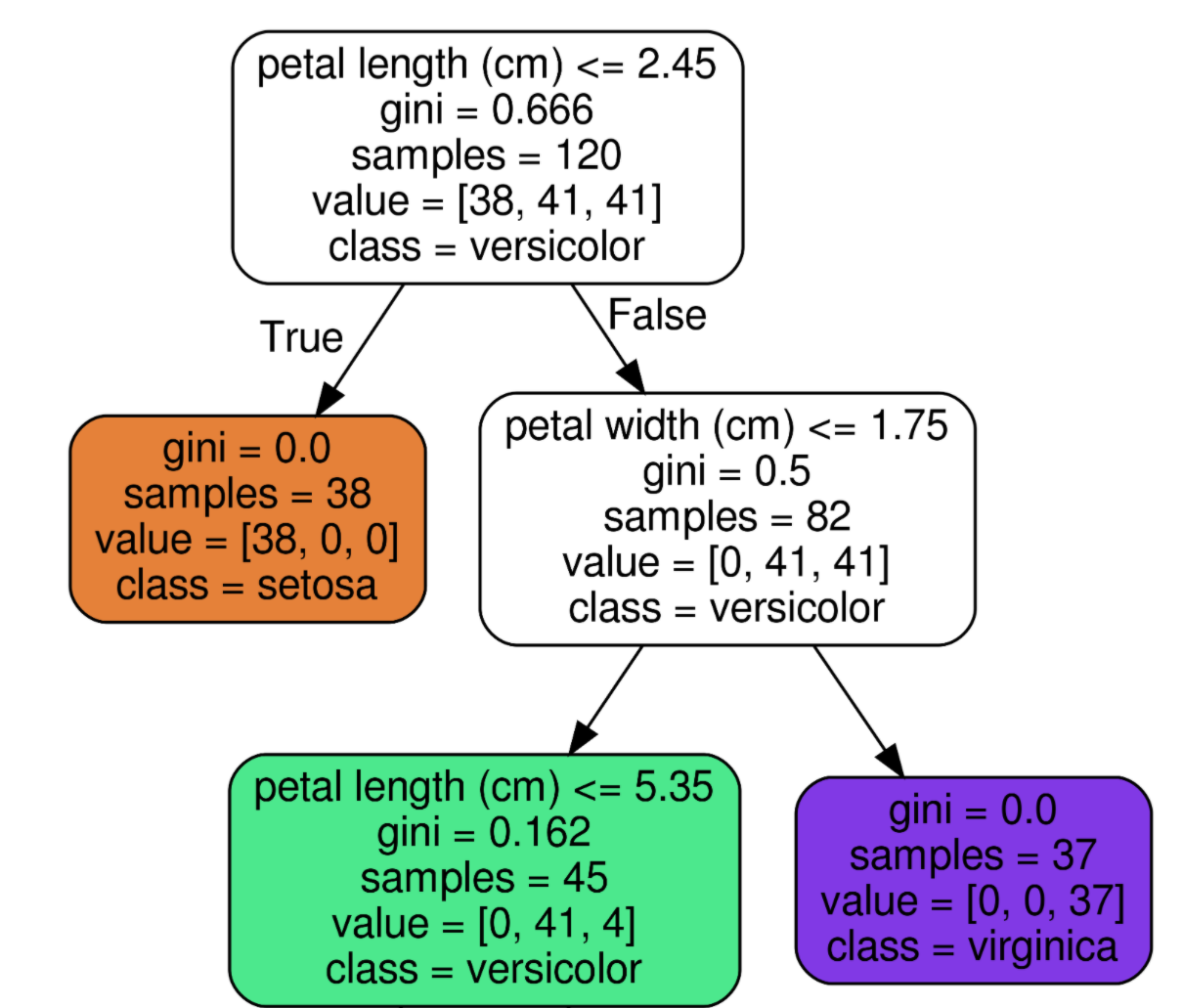
이 그림은 직관적으로 리프 노드와 브랜치 노드를 볼 수 있어서 가져왔다. 자식노드가 없는 리프 노드에서 최종적으로 어떤 클래스인지 결정된다. 그 노드에 도달하기까지의 조건을 만족한다면 거기서 이 꽃이 어떤 종류의 붓꽃인지 예측하는 것이다.

리프노드가 되는 조건?

• 최종 데이터가 오직 "하나의" 클래스 값으로 구성
• 하이퍼 파라미터 조건 충족 ( 뒤에서 자세히 설명)

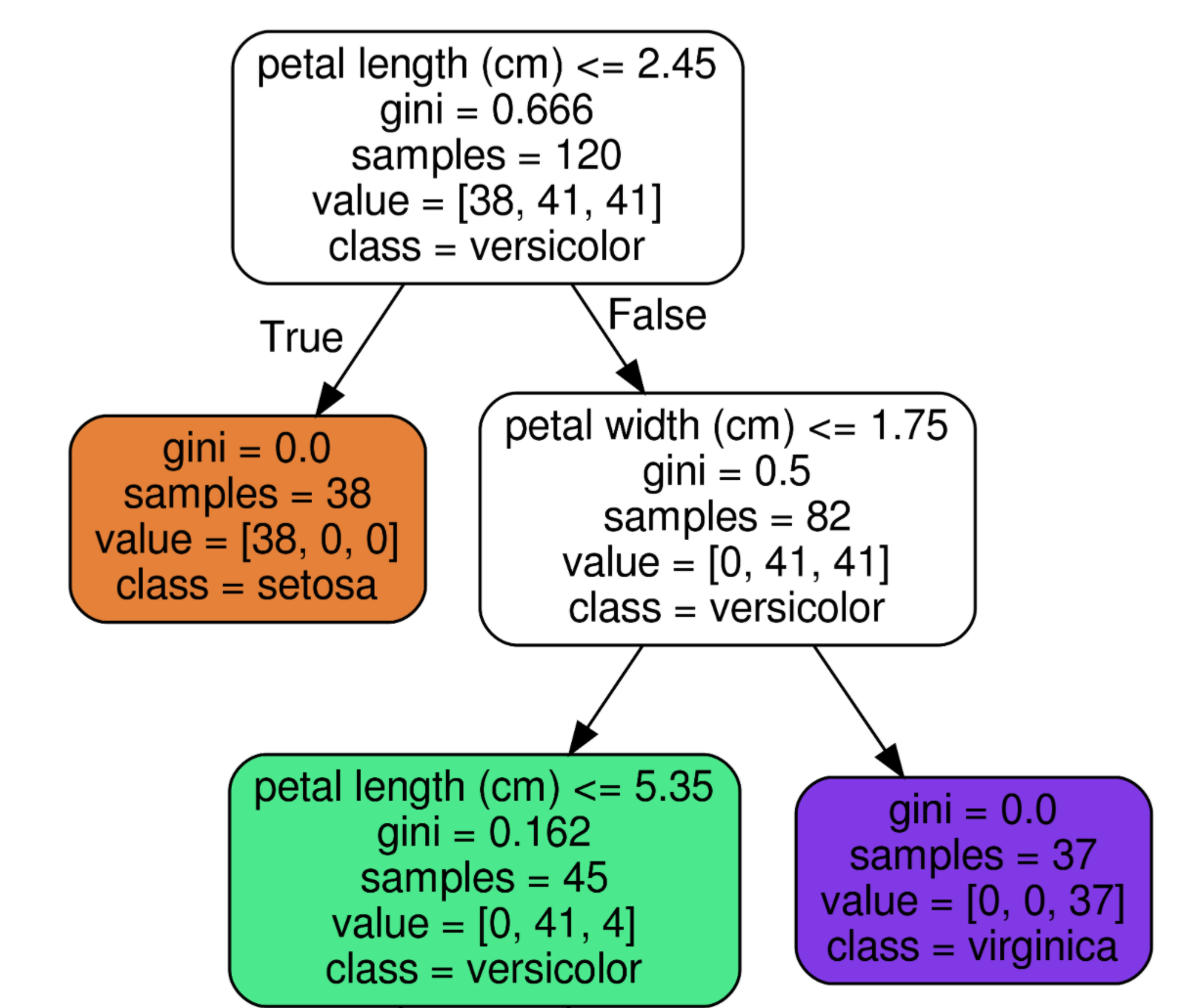
브랜치 노드 안에는 맨 위와 같이 5개의 지표가 존재하고, 리프 노드에는 주황색 노드와 같이 4개의 지표가 존재한다.

맨 위의 노드 구성을 예시로 설명해보겠다.

1. petal length(꽃잎 길이) ≤ 2.45
   • 자식노드를 만들기 위한 규칙조건 (없으면 리프노드라는 증거!)
   • 꽃잎 길이가 2.45 이하인 데이터와 초과인 데이터로 분류하겠다는 의미
2. gini = 0.666
   • 지니계수
   • 아래의 value 분포도를 통해 계산
   • 높을수록 데이터 불균일
3. samples = 120
   • 아직 아무런 조건으로도 나뉘어있지 않은 상황
   • 세 품종 데이터 전체 갯수가 120개
4. value = [38, 41, 41]
   • 품종 순서대로 Setosa 50개, Versicolor 50개, Virginica50개라는 의미
   • 리스트 안의 값을 모두 더하면 samples의 개수와 같음
5. class = versicolor
   • 하위 노드를 가질경우 value에서 가장 많은 값의 품종선택
   • 여기서는 versicolor = virginica 50으로 같으므로 인덱스 작은것 선택

노드 색깔이 의미하는 것

붓꽃 데이터의 레이블 값을 의미, 색깔이 짙어질수록 지니계수가 낮아 데이터가 균일하고 해당 레이블에 속하는 샘플이 많다는 의미이다.

0 : Setosa(주황) 1 : Versicolor(초록) 2 : Virginica(보라)

위의 주황색 노드에서 전체 38개의 샘플이 모두 Setosa이므로 매우 균일한 상태라고 볼 수 있다.

2. 하이퍼 파라미터 변경에 따른 트리 변화

너무 복잡한 트리가 되면 과적합이 발생하여 오히려 예측성능이 낮아질 수 있다. 이를 제어하는 파라미터를 알아보자.

1. max_depth
2. min_samples_split
3. min_samples_leaf

max_depth : 너무 깊어지지 않도록!

적절히 설정하는 것이 중요할 것이다. 너무 간단해도, 너무 복잡해도 성능이 좋지 않을 것이기 때문이다.

min_samples_split : 현재 sample 갯수를 보고 자식을 만들지 말지 결정!

기본 설정값은 2이다. 현재 sample이 2개이고, 두 개가 다른 품종이라면 자식노드를 만들어 분할해야한다. 하지만 이 파라미터를 4로 변경하면 샘플이 다른 품종이 섞인 3개여도 분할을 멈추고 리프노드가 된다. 따라서 자연스레 트리 깊이도 줄어든다.

min_samples_leaf : sample갯수가 이 값 이하가 되도록 부모 규칙 변경!

리프노드가 될 수 있는 조건은 샘플수의 디폴트가 1이다. 즉, 샘플이 하나 남아야 리프노드로 인정되는 것이다. 그래야 한 품종만 남을테니 말이다.

하지만 그러면 트리의 리프노드는 너무 많아지고 더 복잡해진다. 따라서 이 파라미터로 리프노드의 엄격했던 기준을 완화시켜주도록 한다.

"자식 샘플 갯수가 4여도 리프노드로 만들어줄게! 그러니까 규칙을 좀만 널널하게 해줘~"

이런 식이다.

3. 어떤 속성이 좋은 모델을 만들까

사이킷런에는 규칙을 정하는 데 있어 피처(속성)의 중요한 역할 지표를 DecisionTreeclassifierr 객체의 featureimportances 속성으로 제공한다.

반환되는 ndarray값은 피처 순서대로 중요도가 할당되어있다. 막대그래프로 시각화하면 더욱 직관적으로 확인 가능하다.

4. 결정트리 과적합(Overfitting)

청일점, 홍일점처럼 일부 이상치 데이터까지 분류하기 위해서 분할이 자주 일어나면 결정 기준 경계도 많아지게 된다. 이렇게 복잡한 모델은 학습 데이터셋의 특성과 약간만 다른형태의 데이터 셋이 들어오면 제대로 예측할 수 없다.

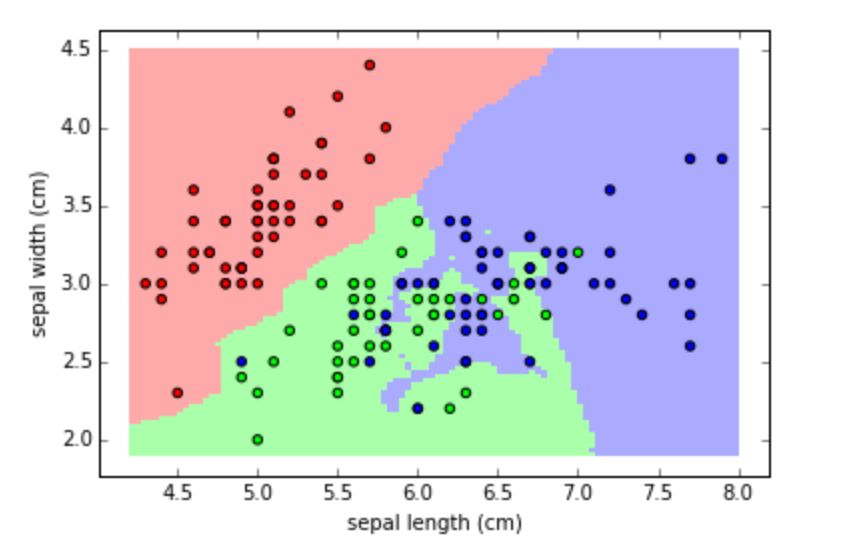
1. 과적합 예시

따라서 하이퍼 파라미터를 변경하여 분류 규칙을 좀 더 일반화시킨다면 이상치에 크게 반응하지 않으면서 예측 성능이 더 좋아질 수 있다.

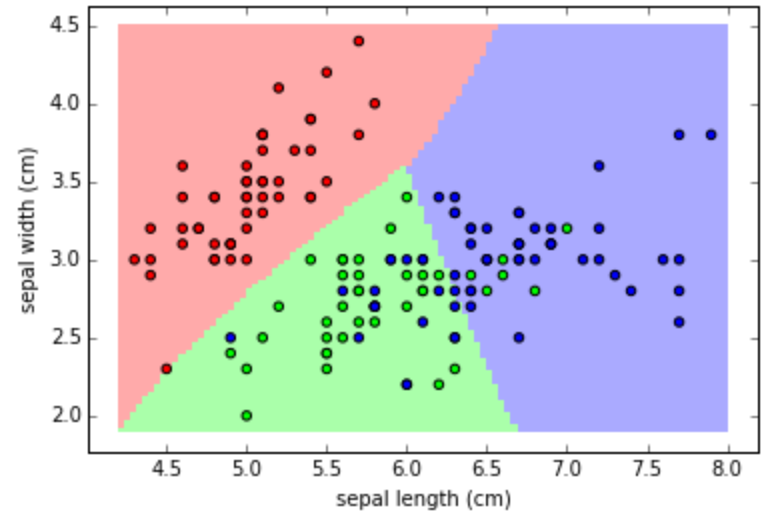
2. 더 일반화된 모델

5. 결정트리 실습 - 사용자 행동 인식 데이터셋

📢글쓰니의 github에서 살펴볼 수 있다!