Syntax Analysis?
쉽게 말하면 lexical analysis의 결과로 만들어진 token들을 문법에 따라 분석하는 parsing 작업을 수행해서 parse tree를 구성하는 작업이다.
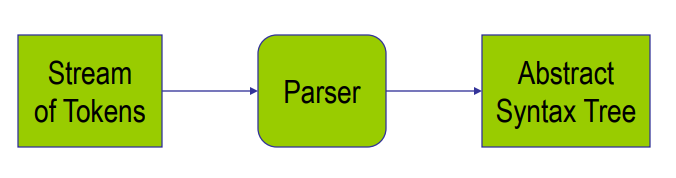
context-free grammer
parse tree를 만들기 위해서 사용하는 문법이다.
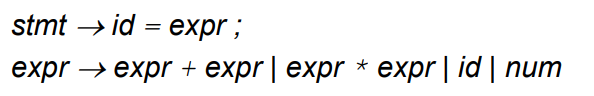
여기서 문법을 쉽게 말하자면 stmt는 문장을 구성하는 방식이다.
무조건 id=expr;의 형태로 이루어져야 한다는 말로 생각하면 된다.(여기서 id는 변수)
expr→ 이 문법은 expr가 더하기와 곱하기 수식을 허용할 뿐만 아니라 숫자와 변수를 저장할 수 있다는 것을 의미한다.
Derivation
Derivation을 설명하기 전에 terminal과 non-terminal에 대해서 알고 가야 하는데

여기에서 X,Y 를 제외하고는 다른 수식으로 바뀔 수 있기 때문에 non-terminal이고 X,Y은 terminal이다. (<>붙어 있는 것들은 non-terminal이라 생각하면 된다.)
즉, 특정 값들로 고정되어 있는 식을 terminal, 고정되지 않은 식을 non-terminal이라고 한다.
Derivation은 non-terminal인 식을 terminal들로 구성된 식으로 바꾸는 과정이다.
예를 들어, X=Y-X*X라는 식을 저 규칙에 맞게 derivation 해보자
<stmt_list> => <stmt>
=> <var> = <expr>
=> X = <expr>
=> X = <expr> * <expr>
=> X = <expr> * <var>
=> X = <expr> * X
=> X = <expr> - <expr> * X
=> X = <var> - <expr> * X
=> X = Y - <expr> * X
=> X = Y - <var> * X
=> X = Y - Y * X
이러한 과정을 통해서 derivation이 이루어 진다.Parse Tree
derivation 과정을 tree로 만들어낸게 parse tree이다.
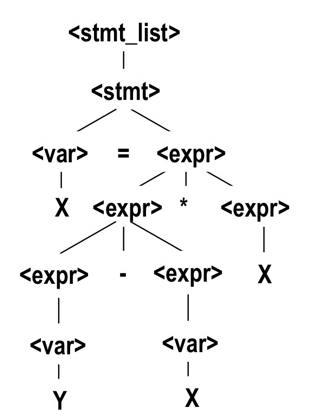
여기에서 derivation 과정에 따라서 tree가 다르게 그려지는데, 같은 식에서 여러 개의 parse tree가 나오는 것을 ambiguity라고 한다.
이 ambiguity를 없애주기 위해 context-free grammer를 우선순위가 있도록 만들어야한다.
ex) 괄호 > 곱하기,나누기 > 더하기,빼기
위의 식을 ambiguous하지 않게 바꾸기 위해서는
<expr> -> <expr>-<temp> | <var> | <temp>
<temp> -> <temp>*<var> | <var>
<var> -> X | Y
-> parsing 우선순위는 <expr> -> <temp> -> <var>
이렇게 수정하면 무조건 *를 먼저 계산하기 때문에 하나의 parse tree가 나온다.