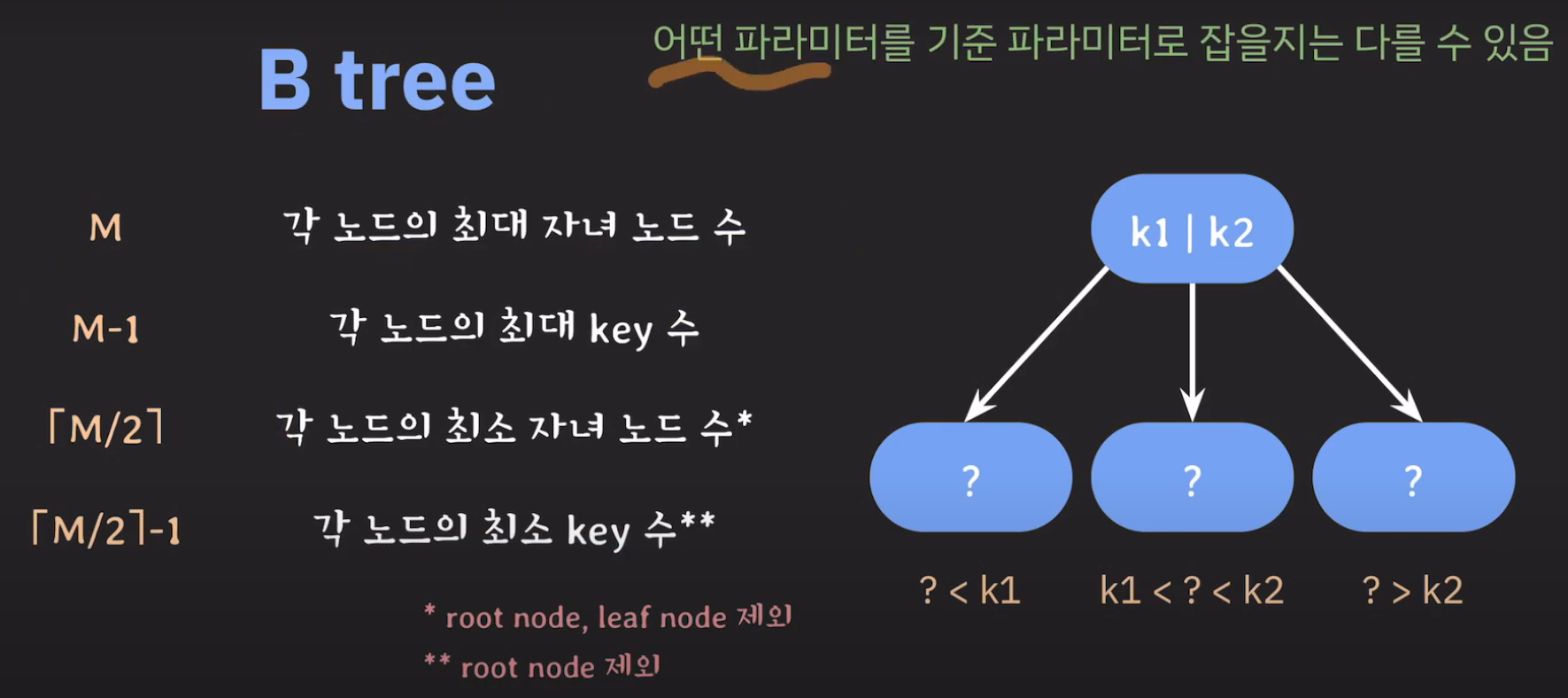
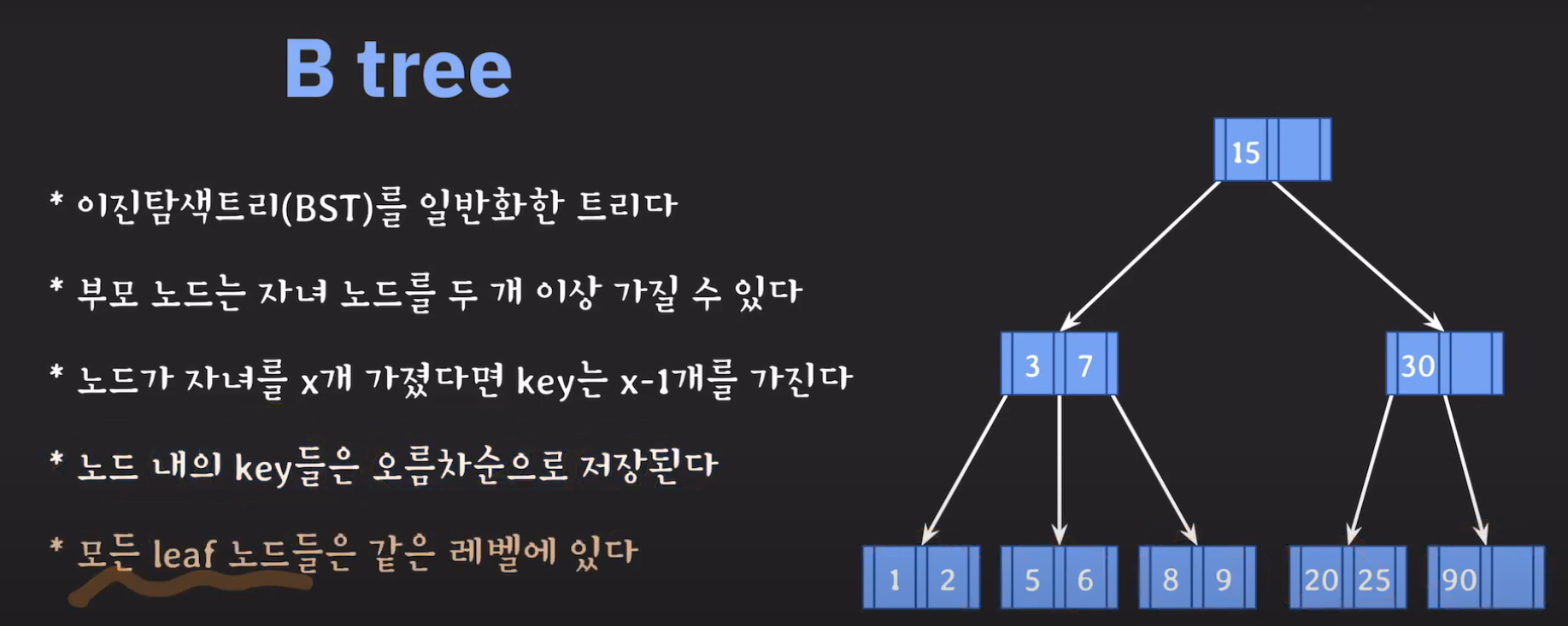
B Tree 개념
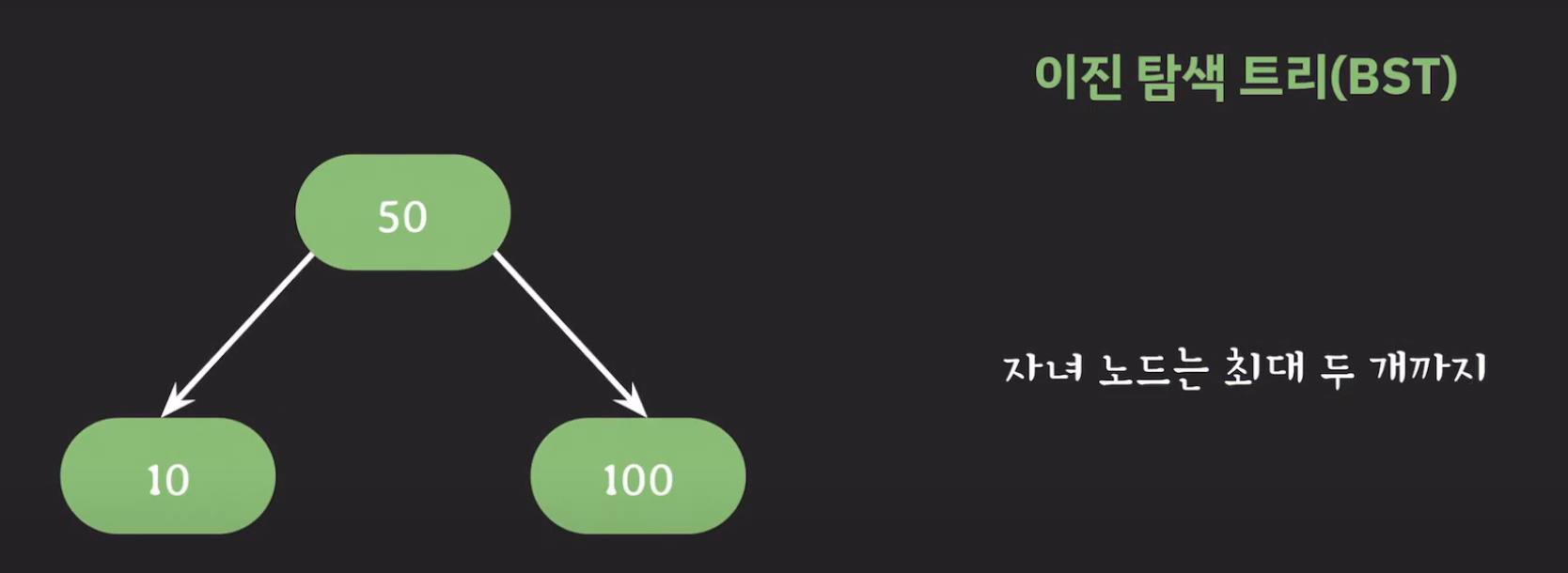
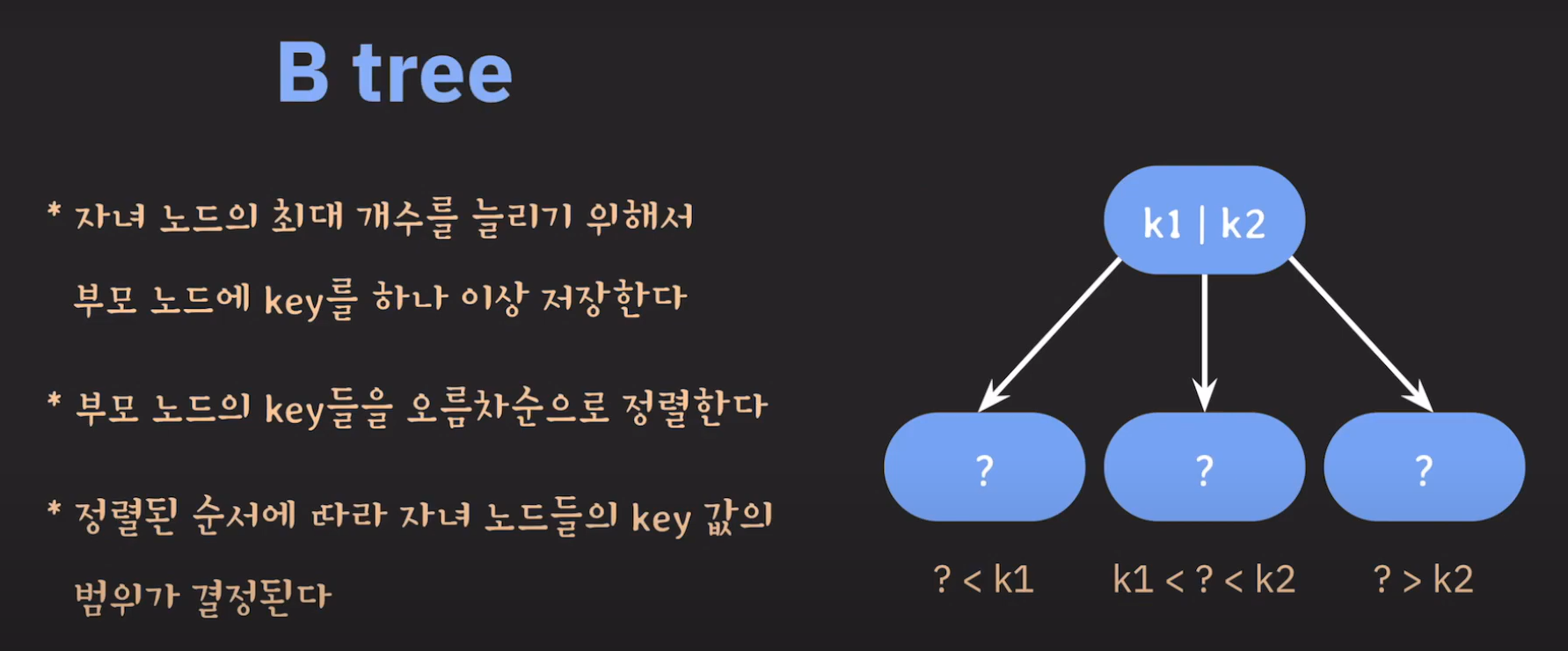
기존의 BST는 자녀 노드가 최대 2개였습니다. 그러나 자녀 노드를 세 개까지 가지고 싶다면 어떻게 해야 할까요?
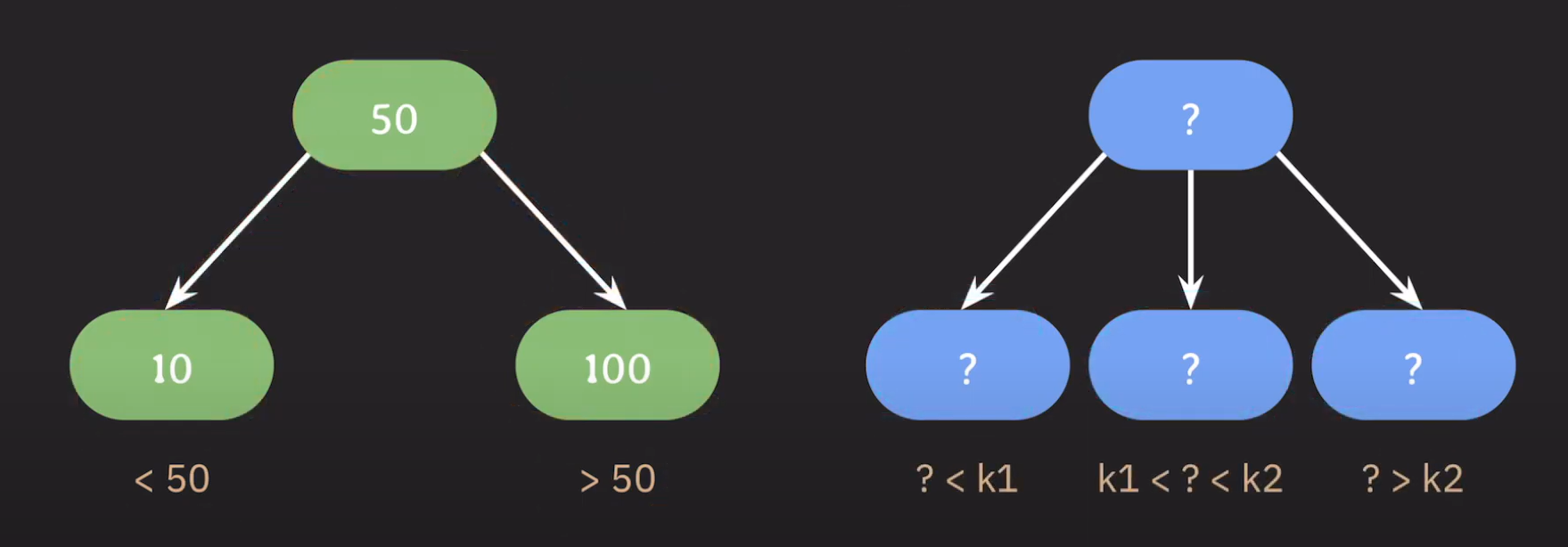
왼쪽 자녀 노드들은 부모 노드보다 작은 값으로, 오른쪽 자녀 노드들은 부모 노드보다 큰 값으로 정했던 것처럼 특정한 두 값을 기준으로 범위를 나눠 적용하면 될 것입니다.
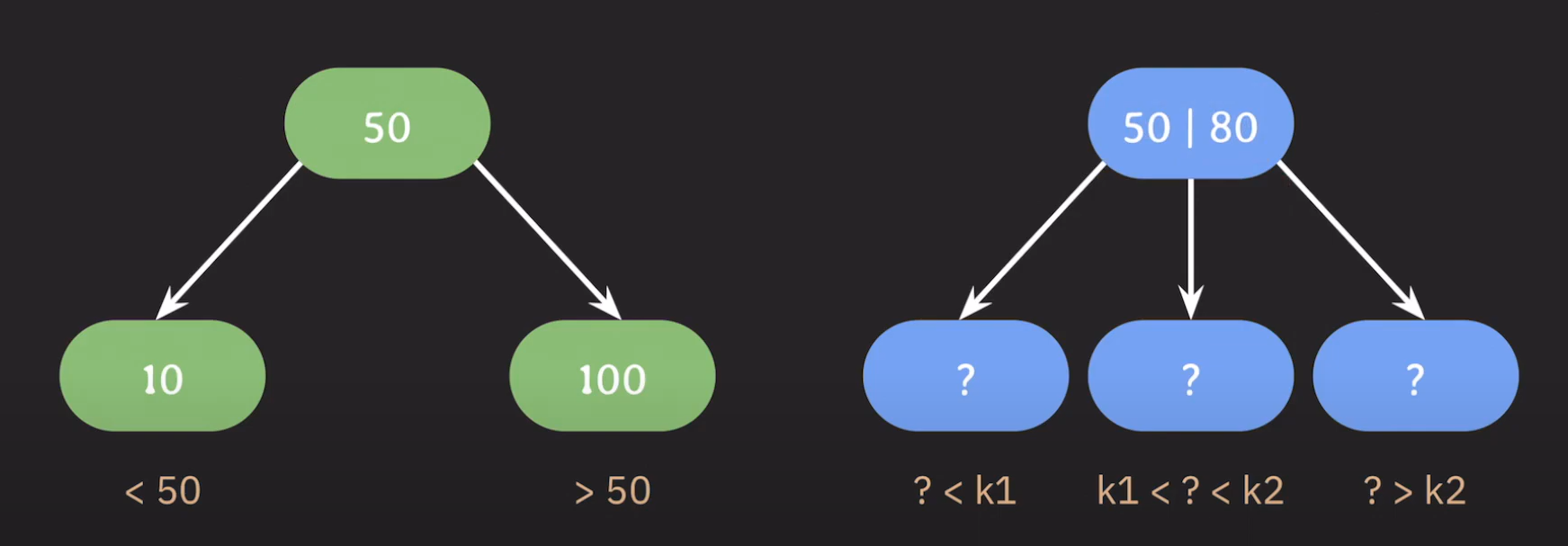
따라서 노드에 한 개의 값이 아니라 두 개의 값을 저장하게 됩니다.
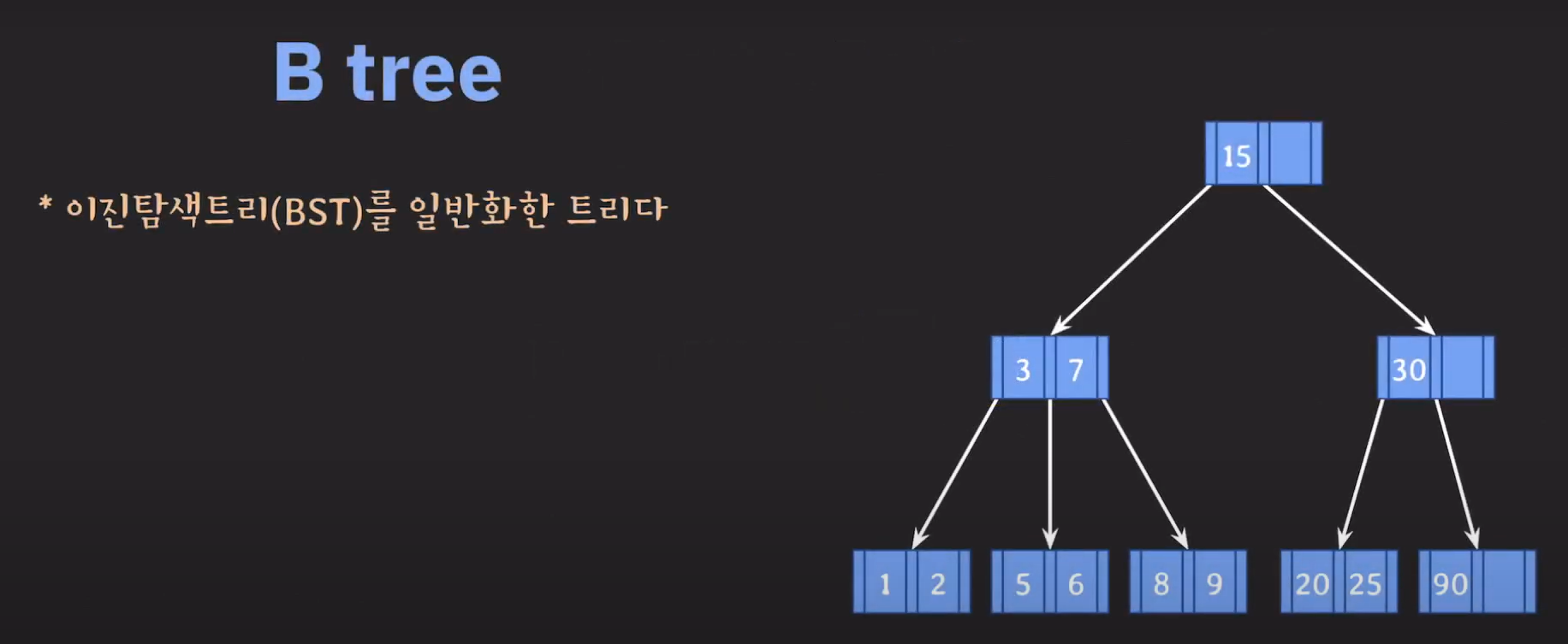
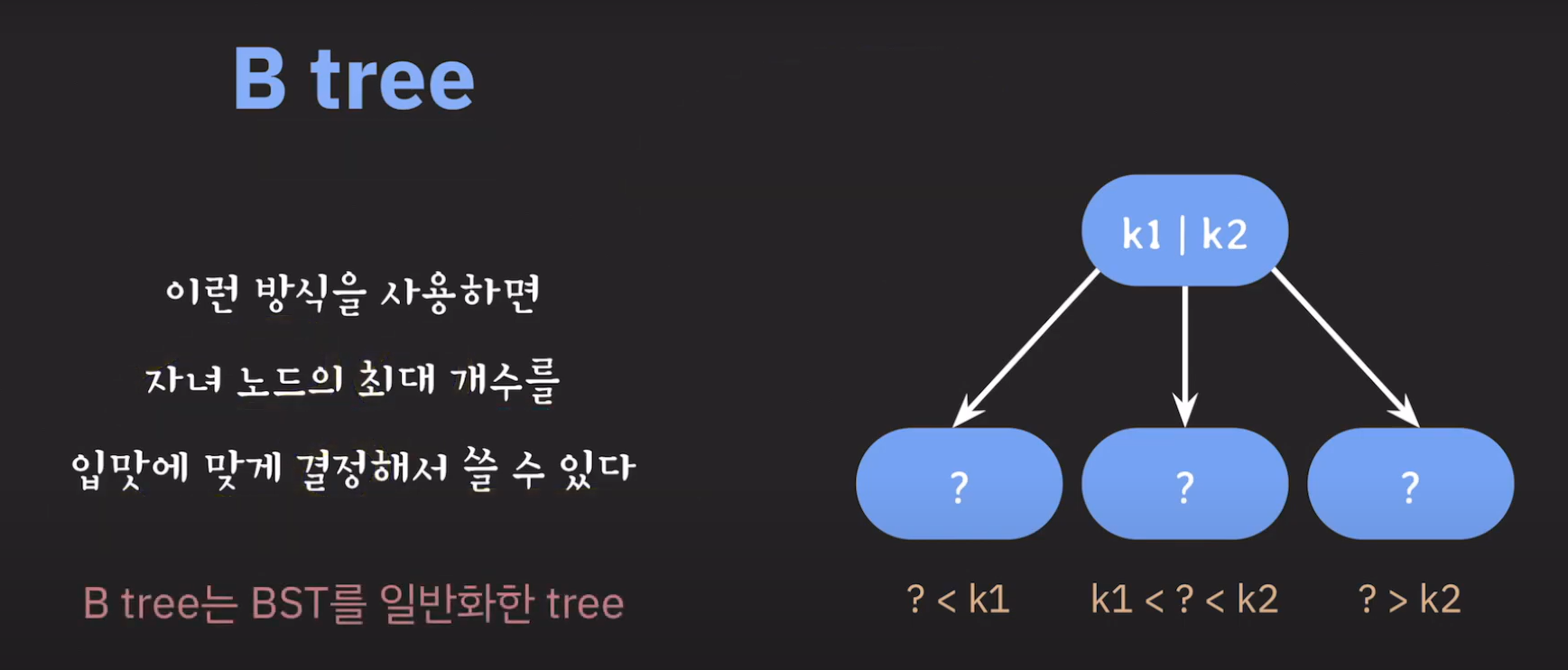
따라서 이와 같은 특징을 갖는 Tree를 B Tree라고 합니다.
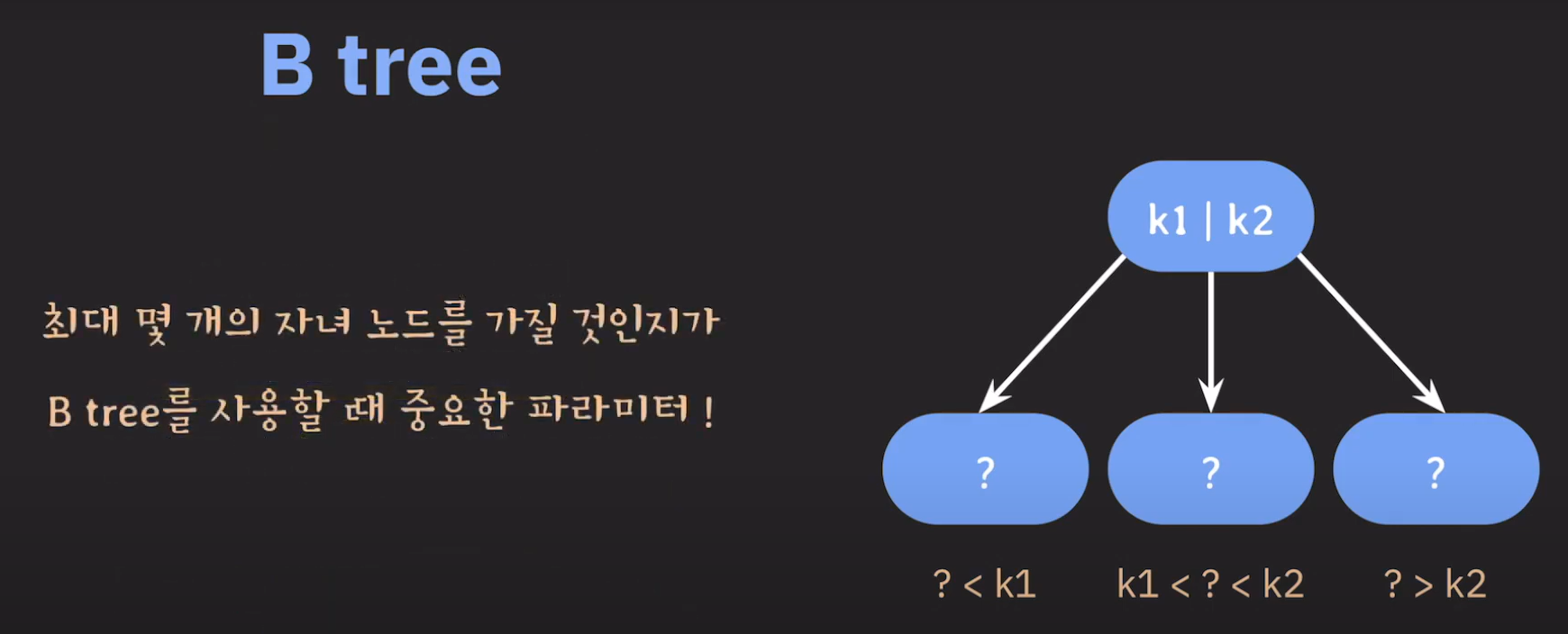
위와 같은 경우는 3차 B Tree라고 부릅니다.
B Tree 삽입
B Tree 데이터 삽입 관련 두 가지 포인트
- 추가는 항상 leaf 노드에 합니다.
- 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진합니다.
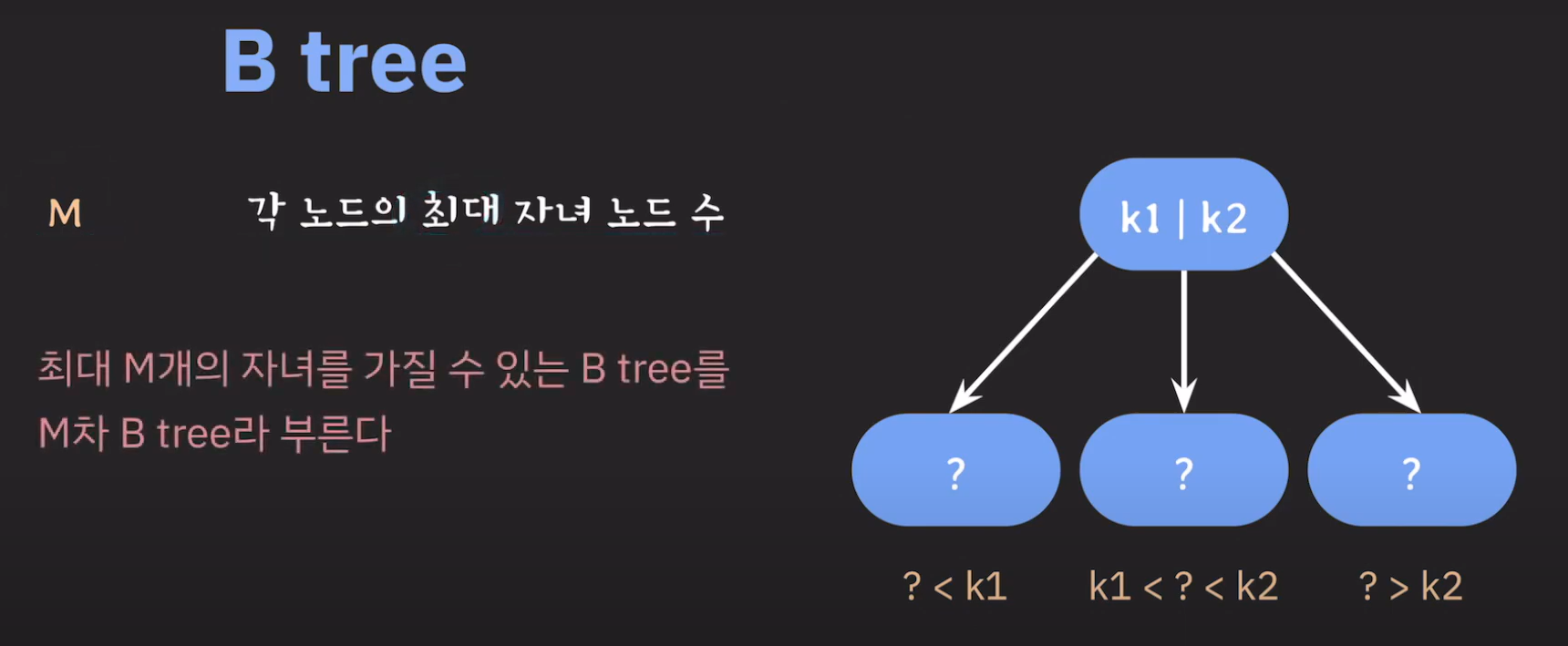
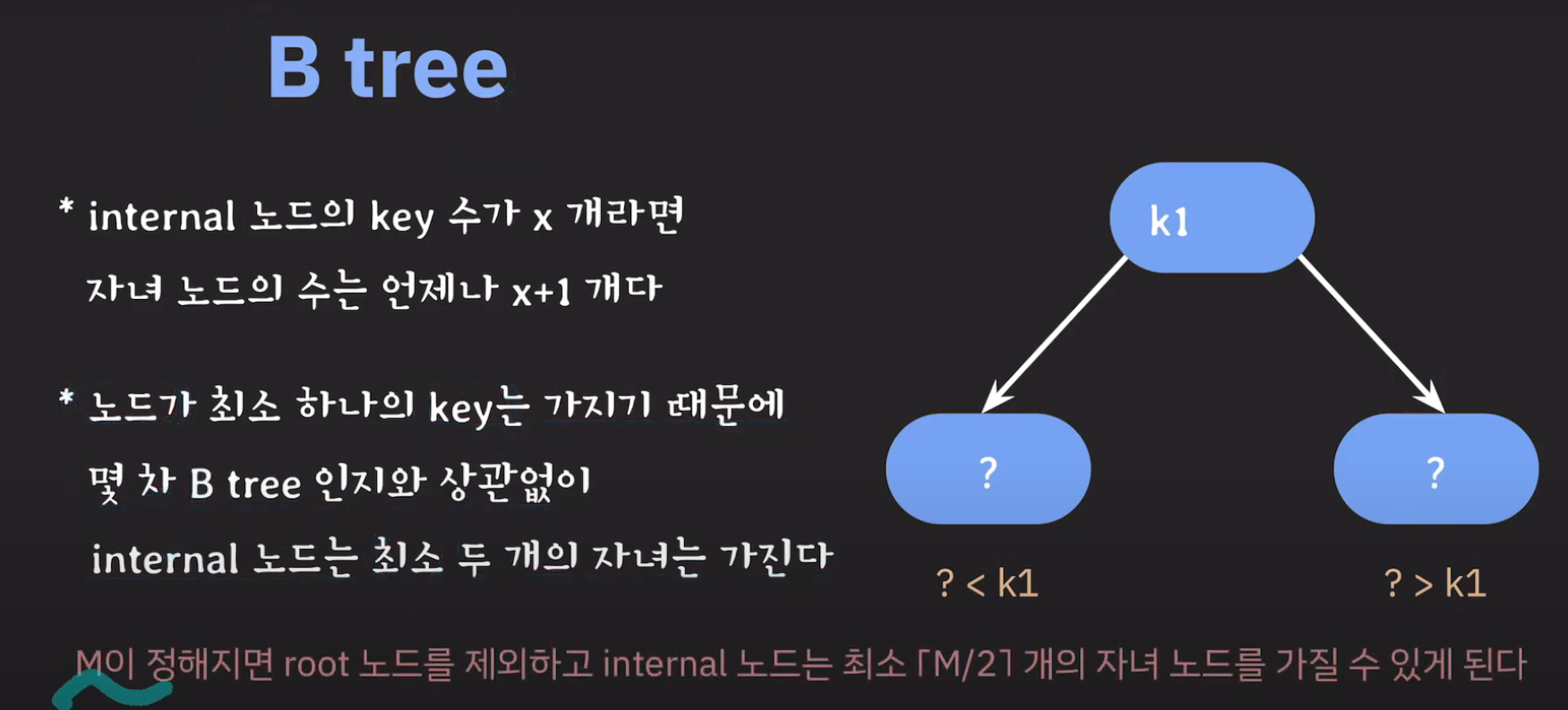
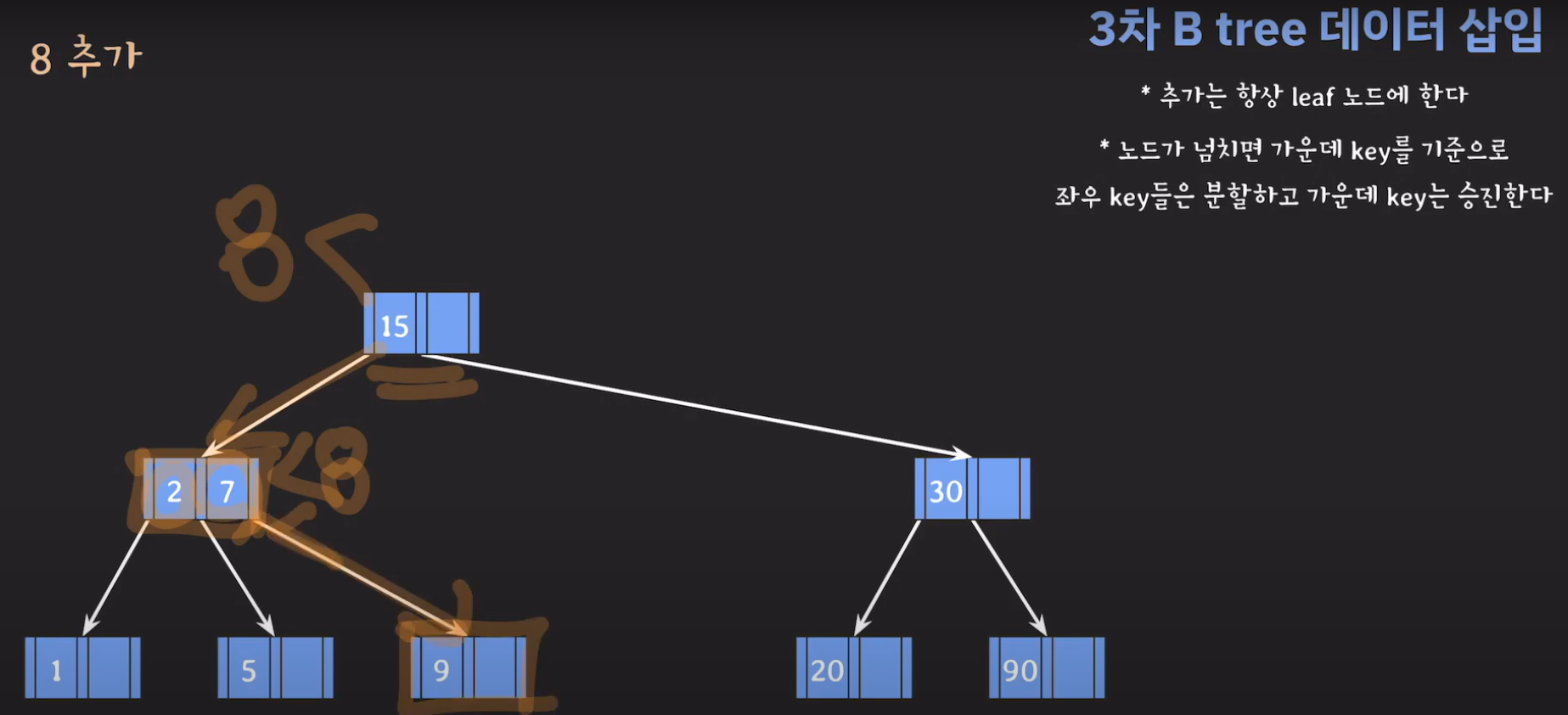
여기서 노드가 넘친다는 뜻은 각 노드의 최대 자녀수를 M이라고 정했을 때 각 노드의 key값이 M-1개를 넘어가는 경우를 말합니다.
- 3차 B Tree이므로 각 노드는 2개의 key를 가질 수 있습니다.
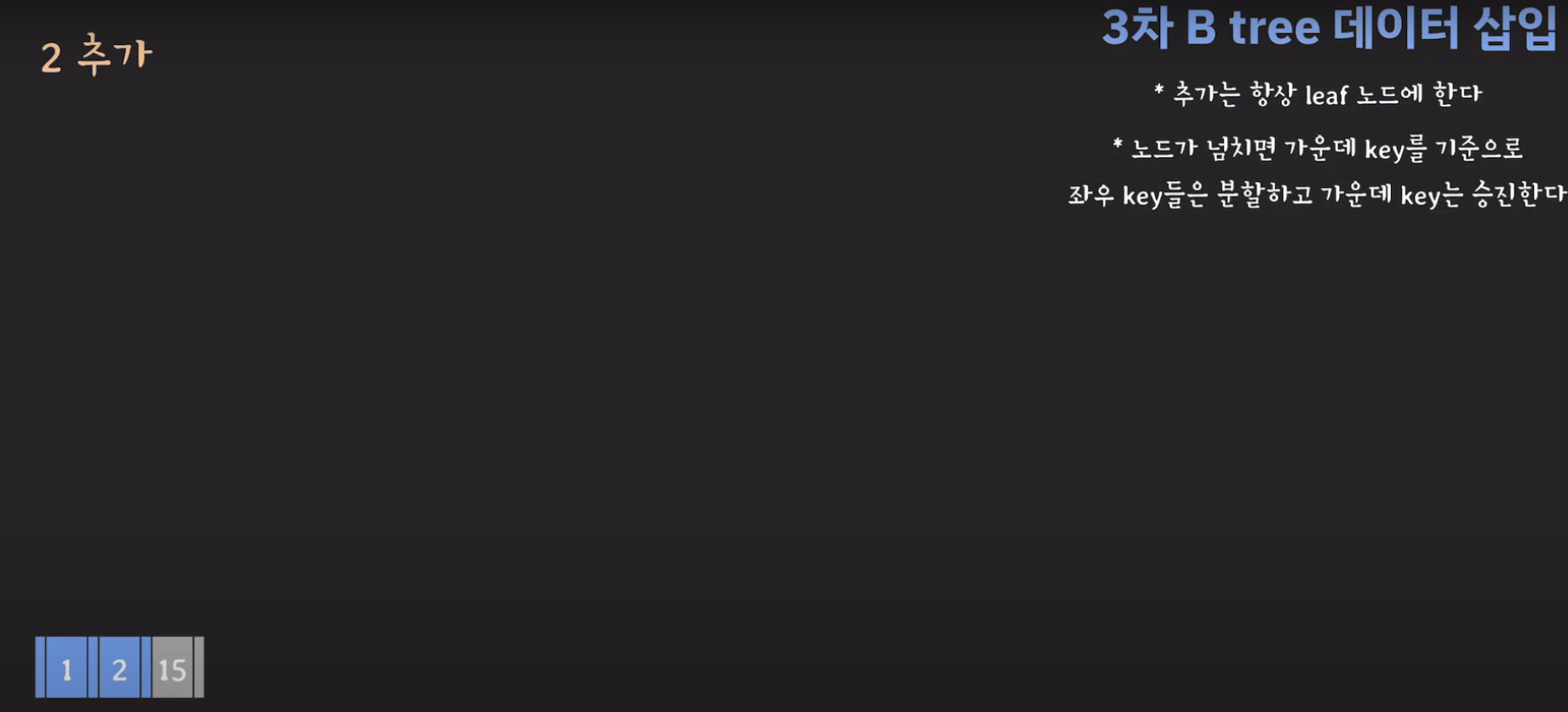
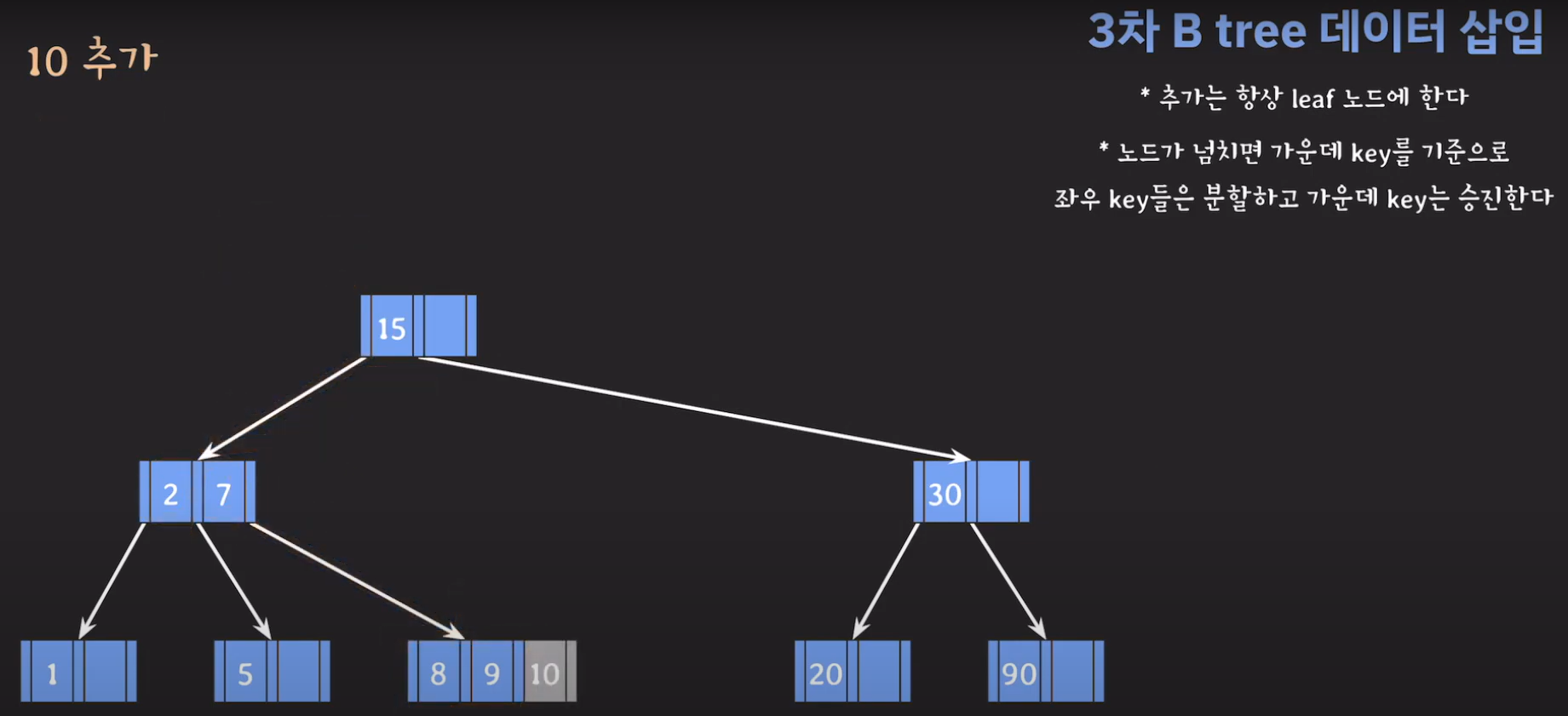
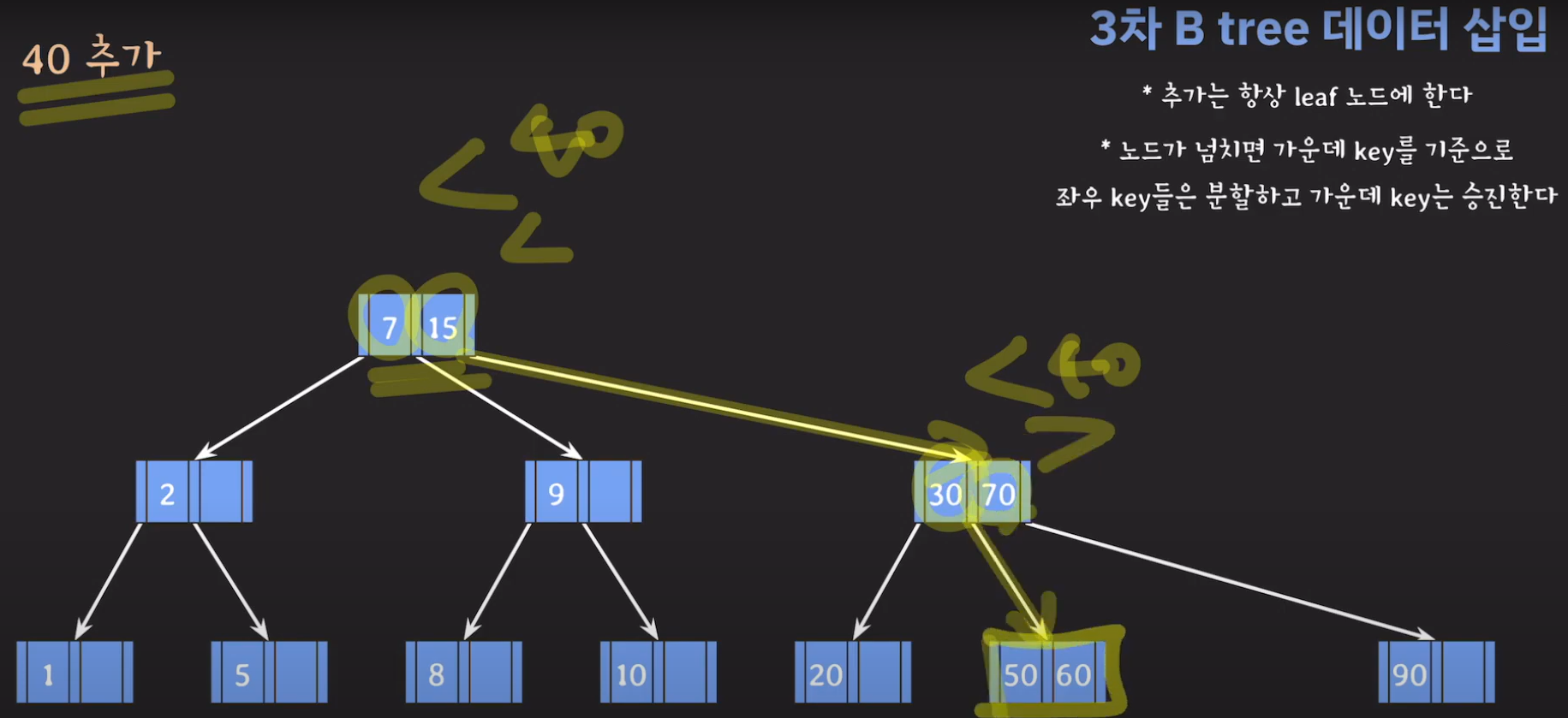
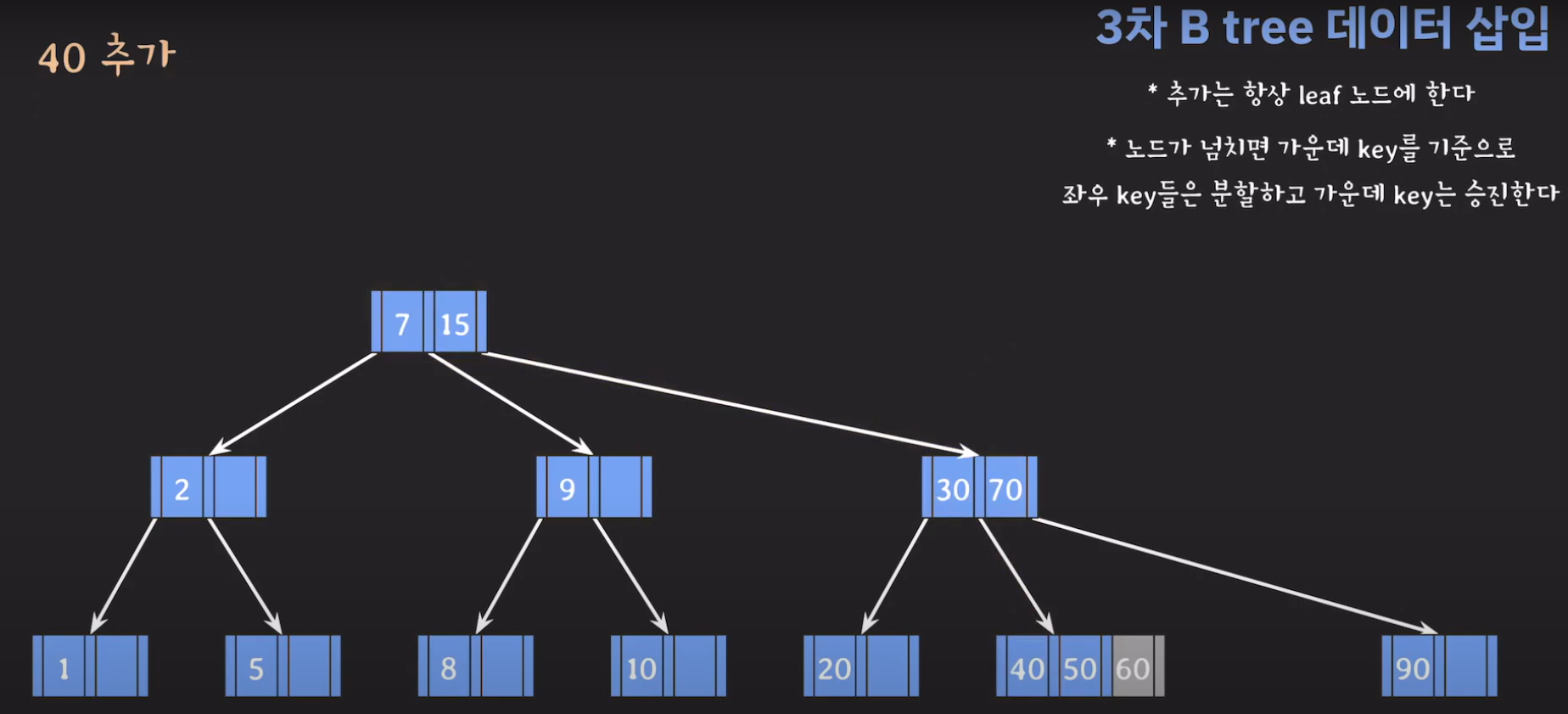
- 데이터를 추가할 때 오름차순으로 저장해야 합니다.
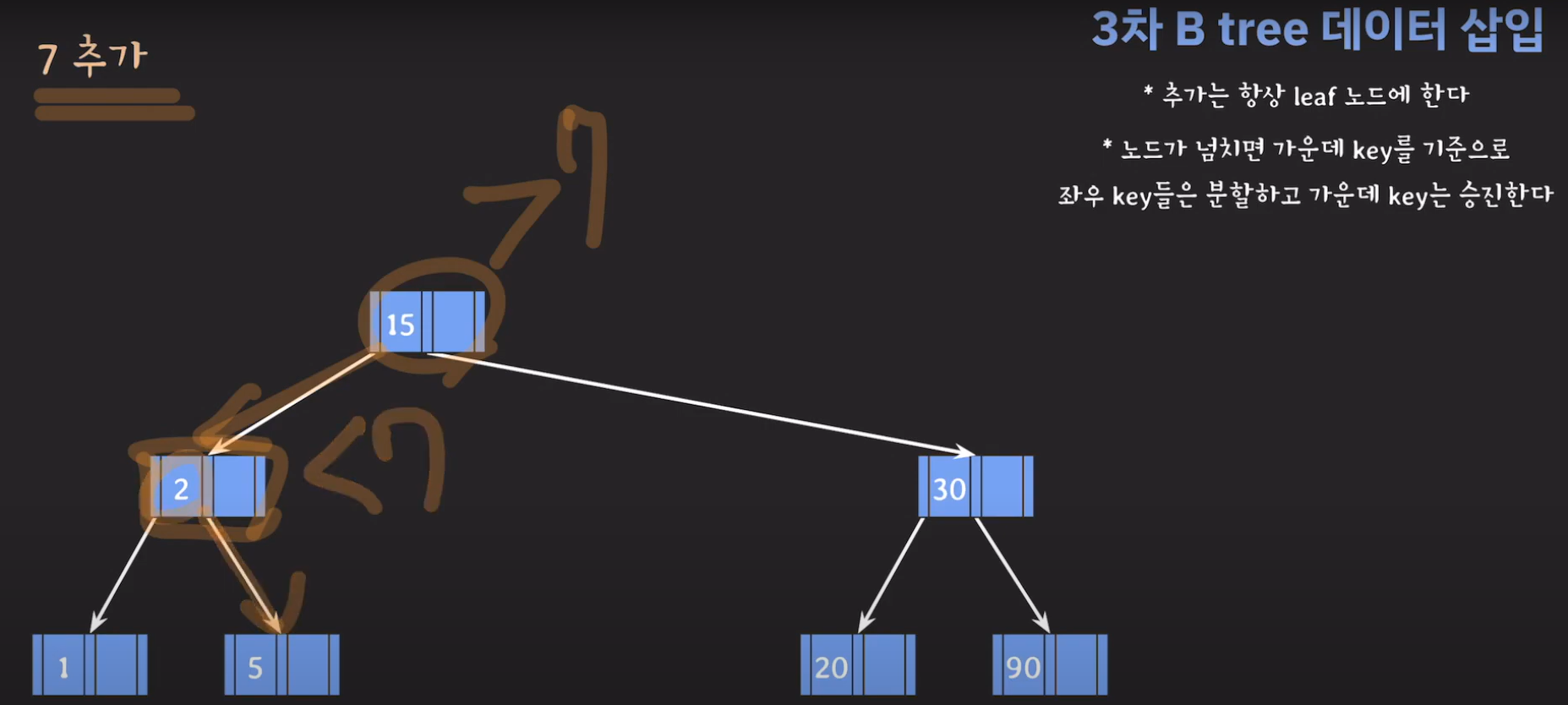
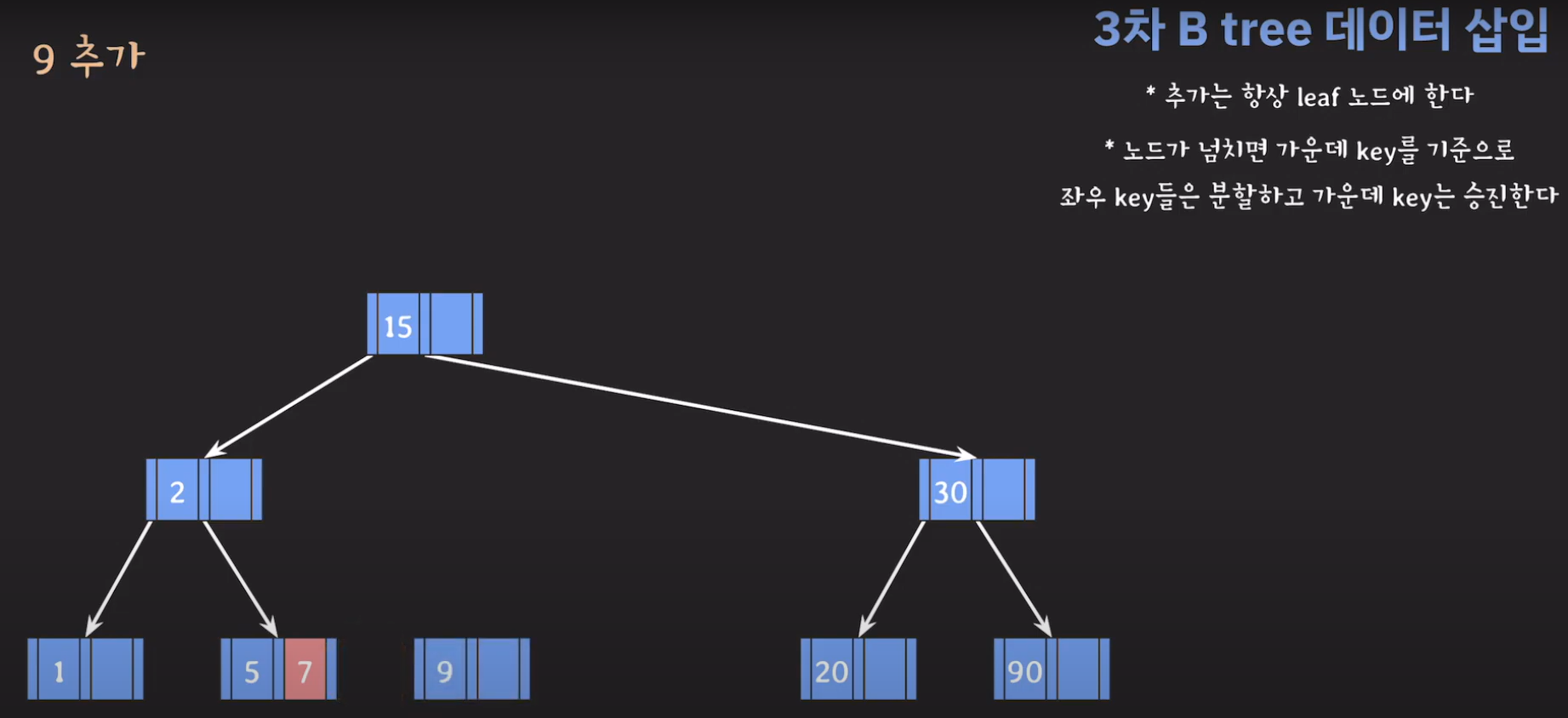
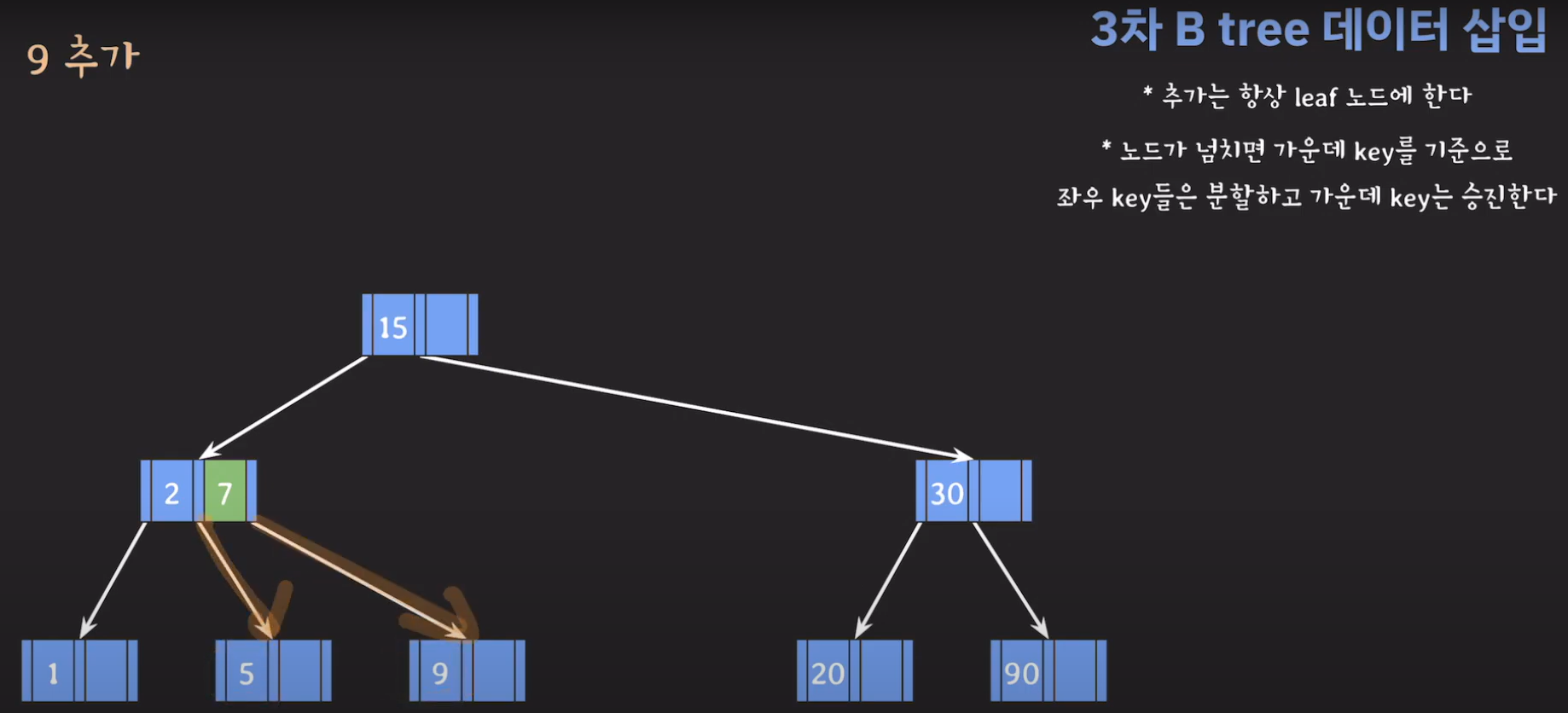
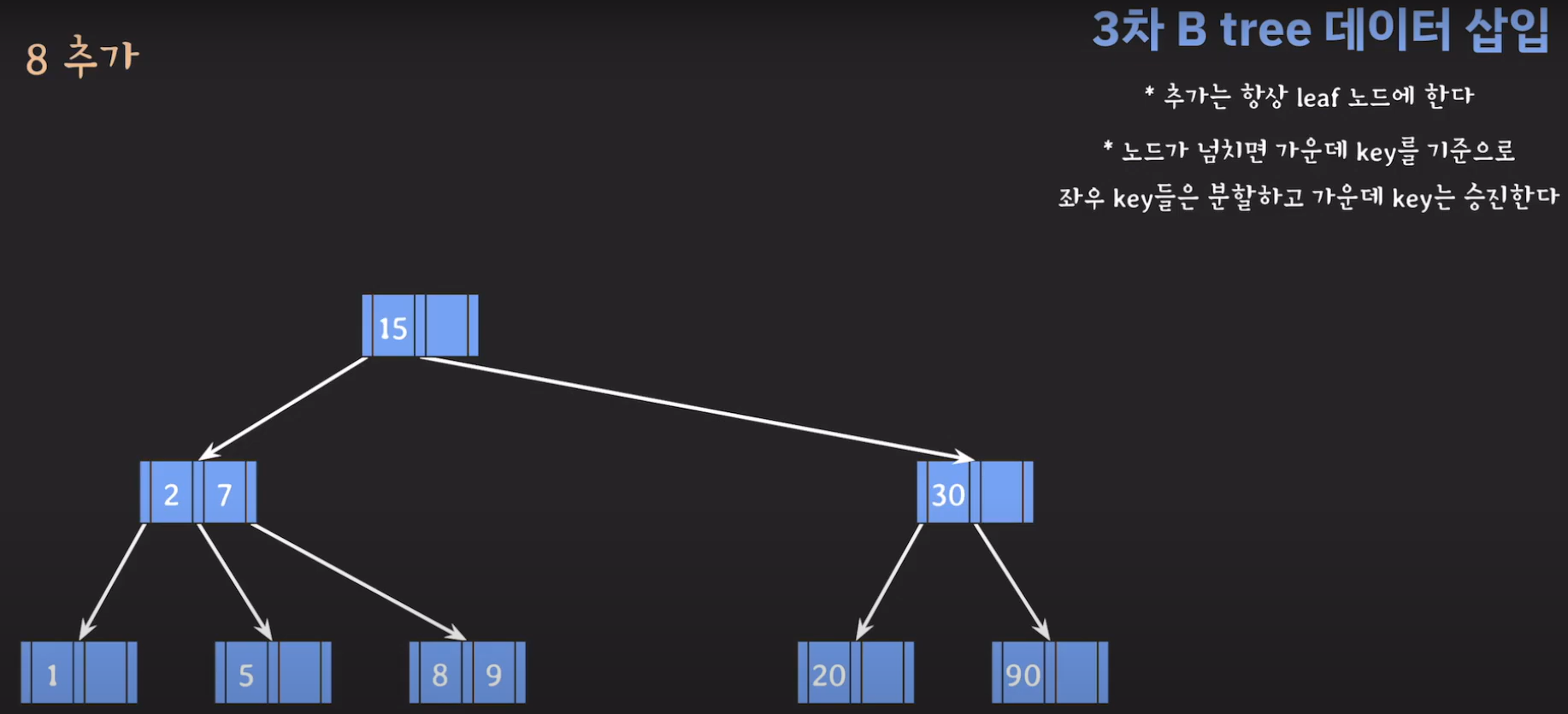
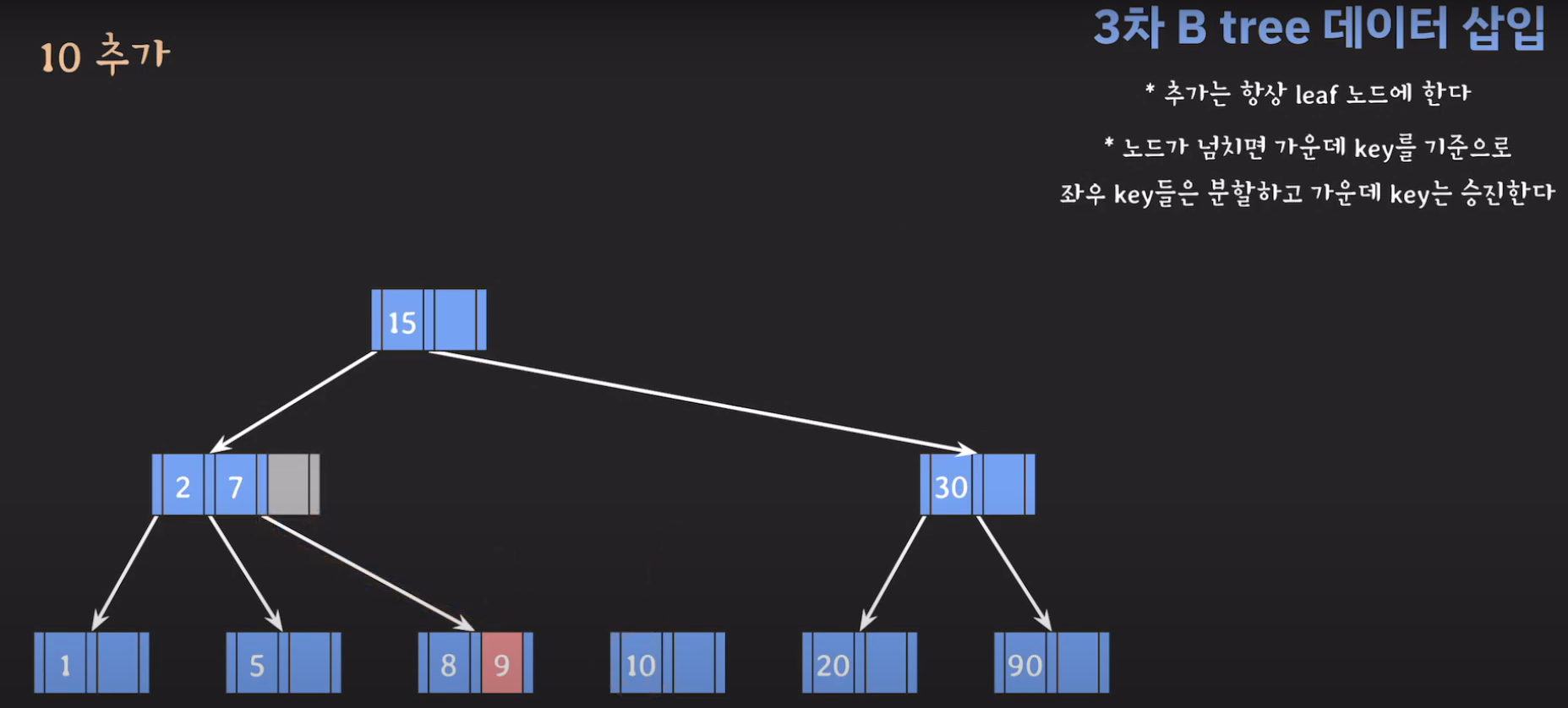
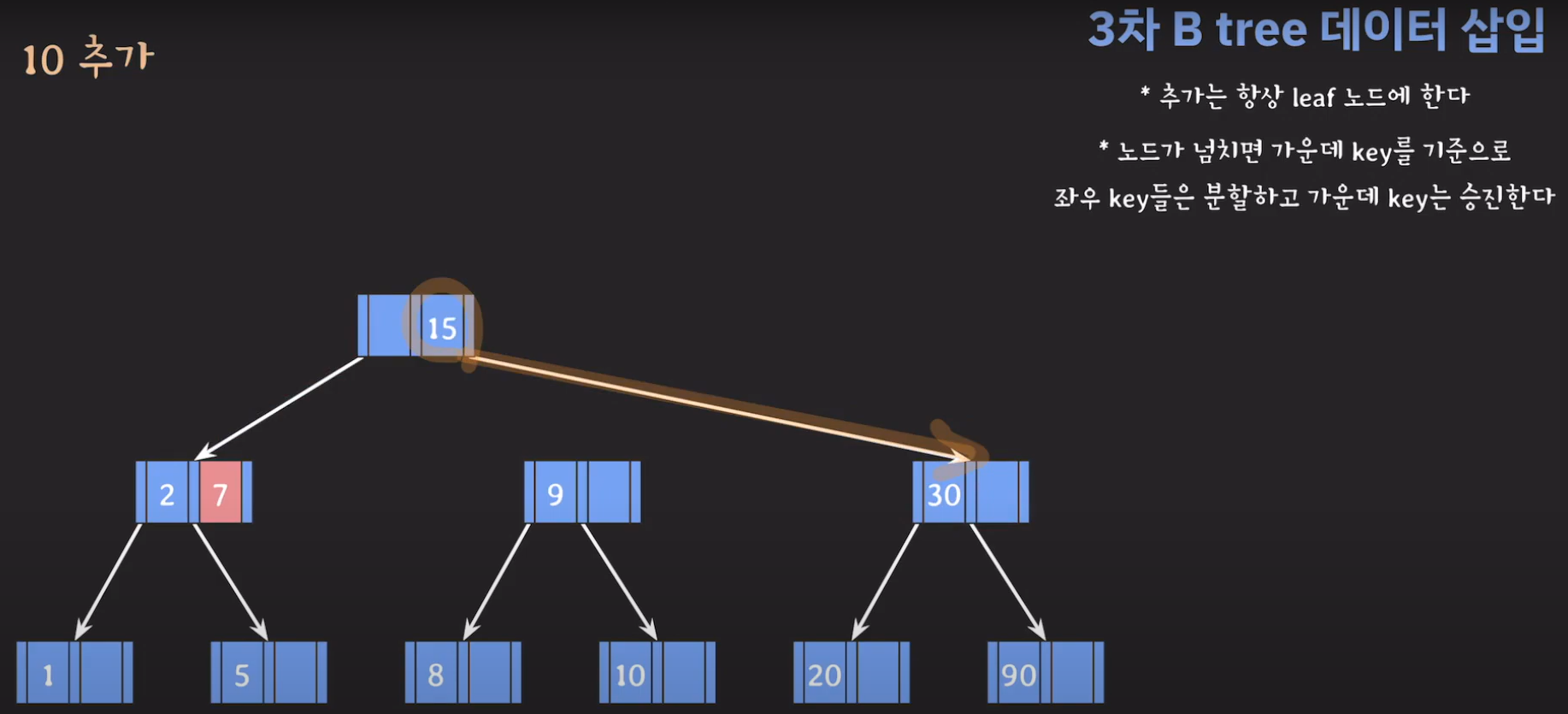
- 지금 상황에서 노드가 넘쳤기 때문에 가운데 key를 기준으로 분할한 후 가운데 key를 승진시킵니다.
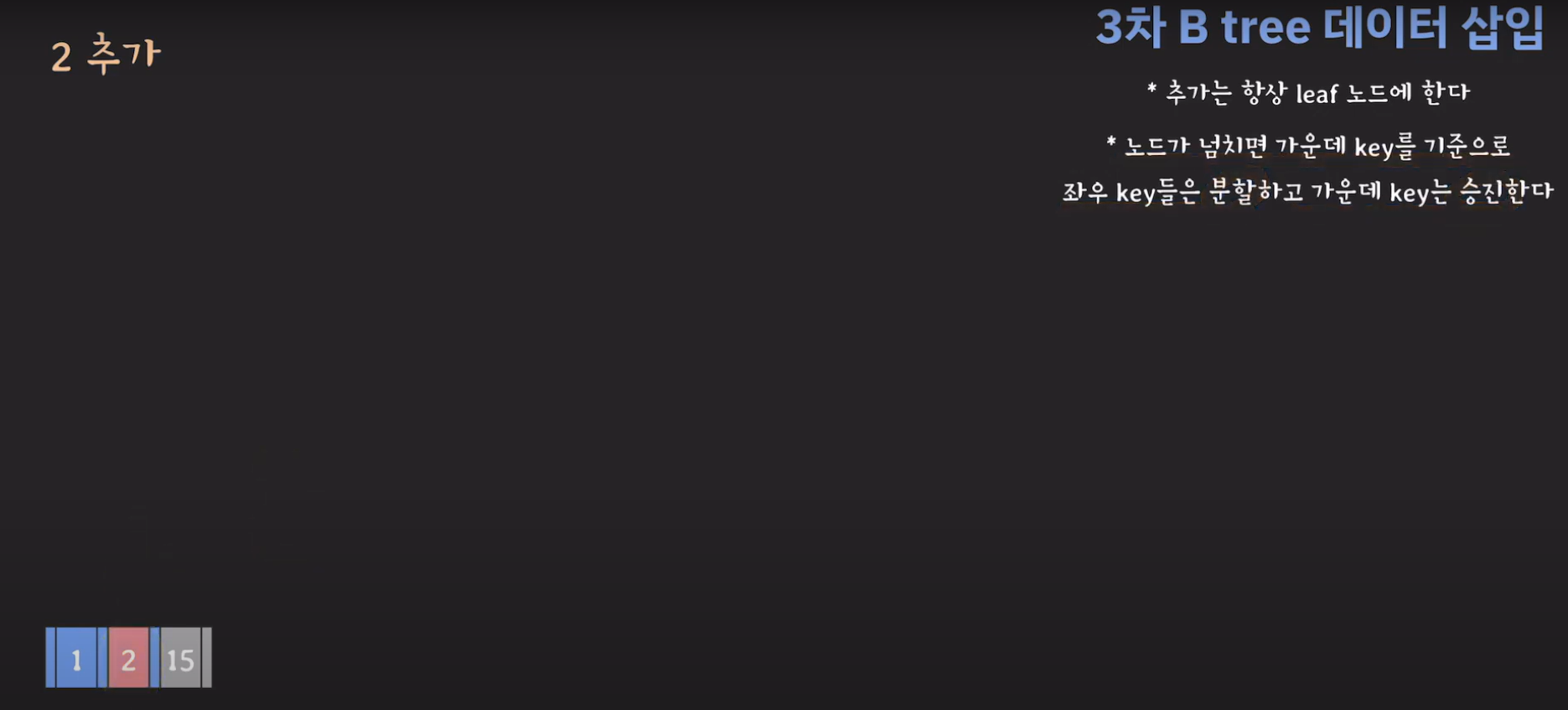
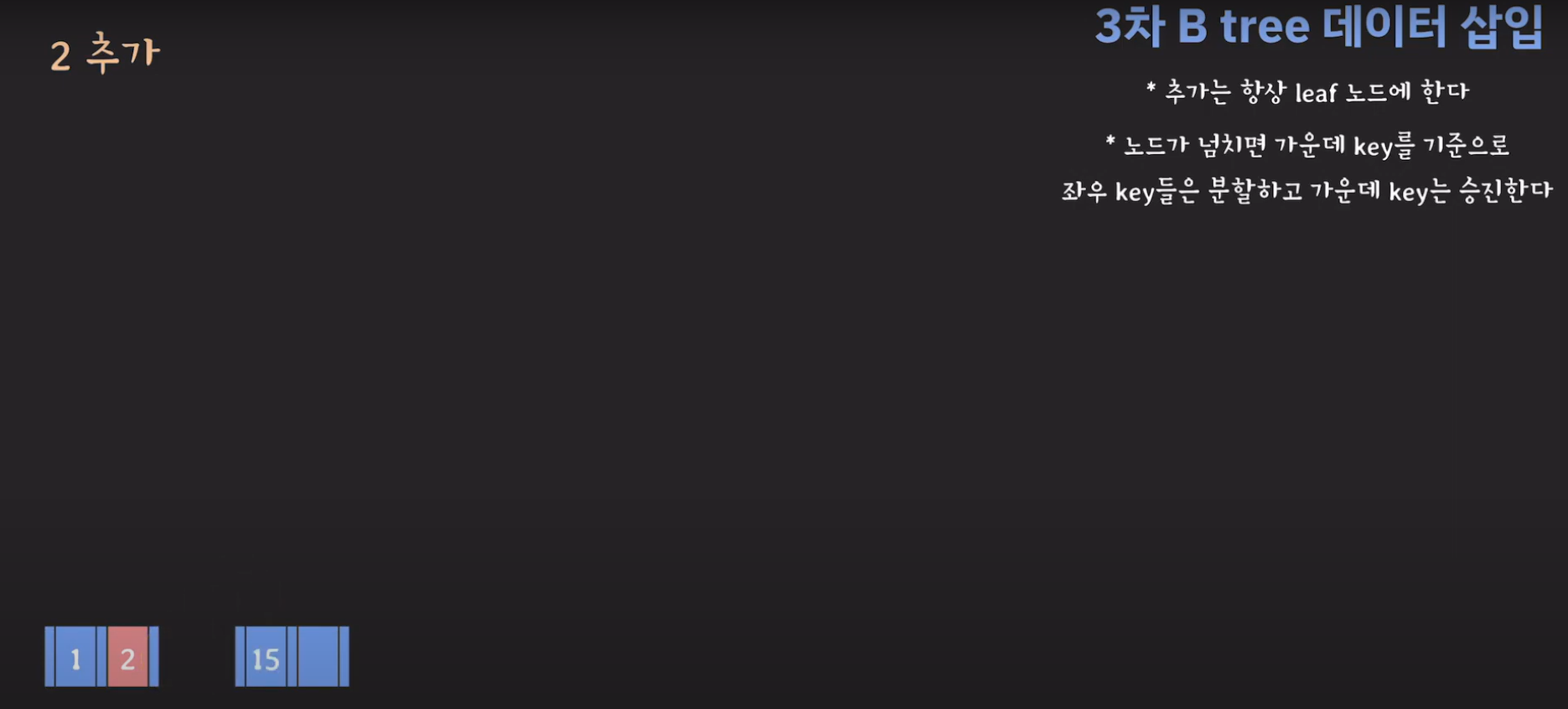
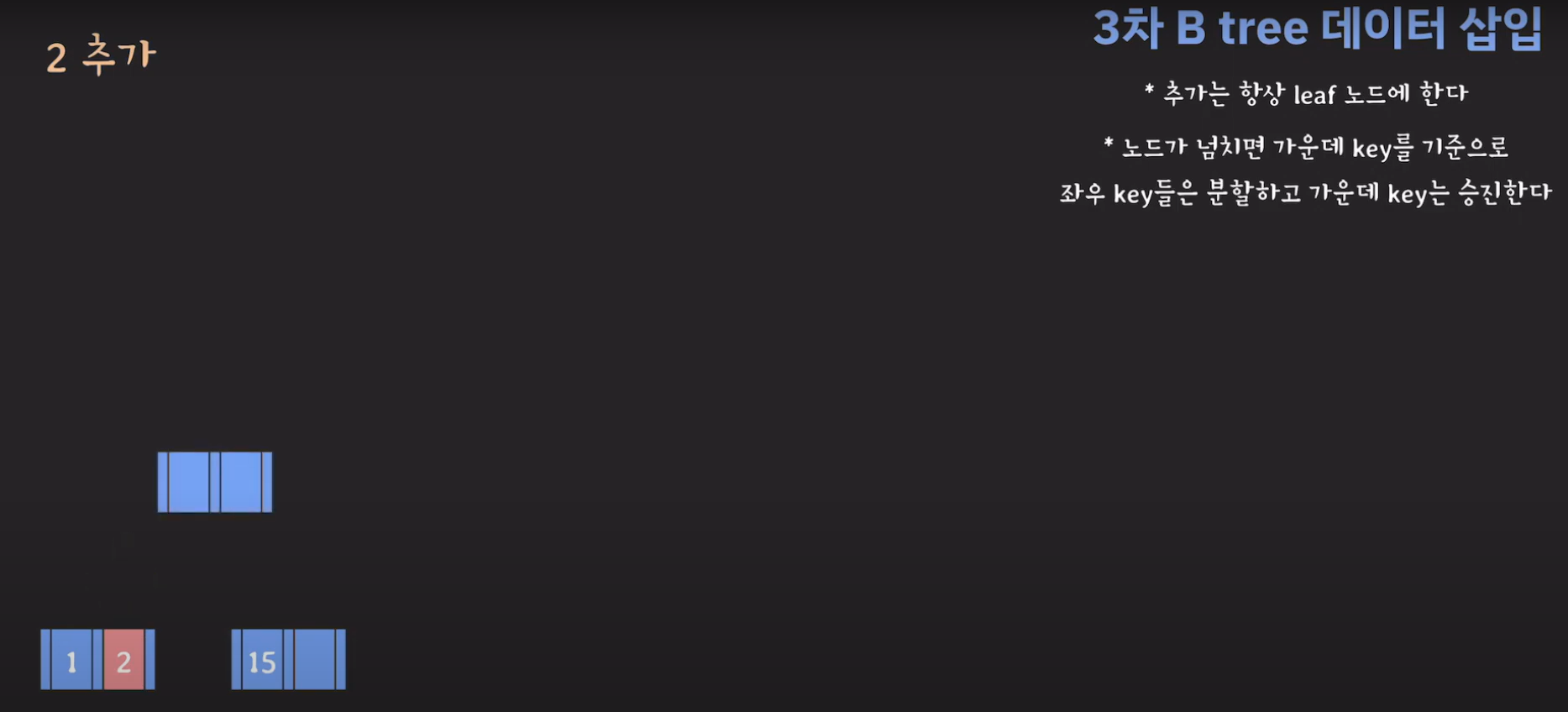
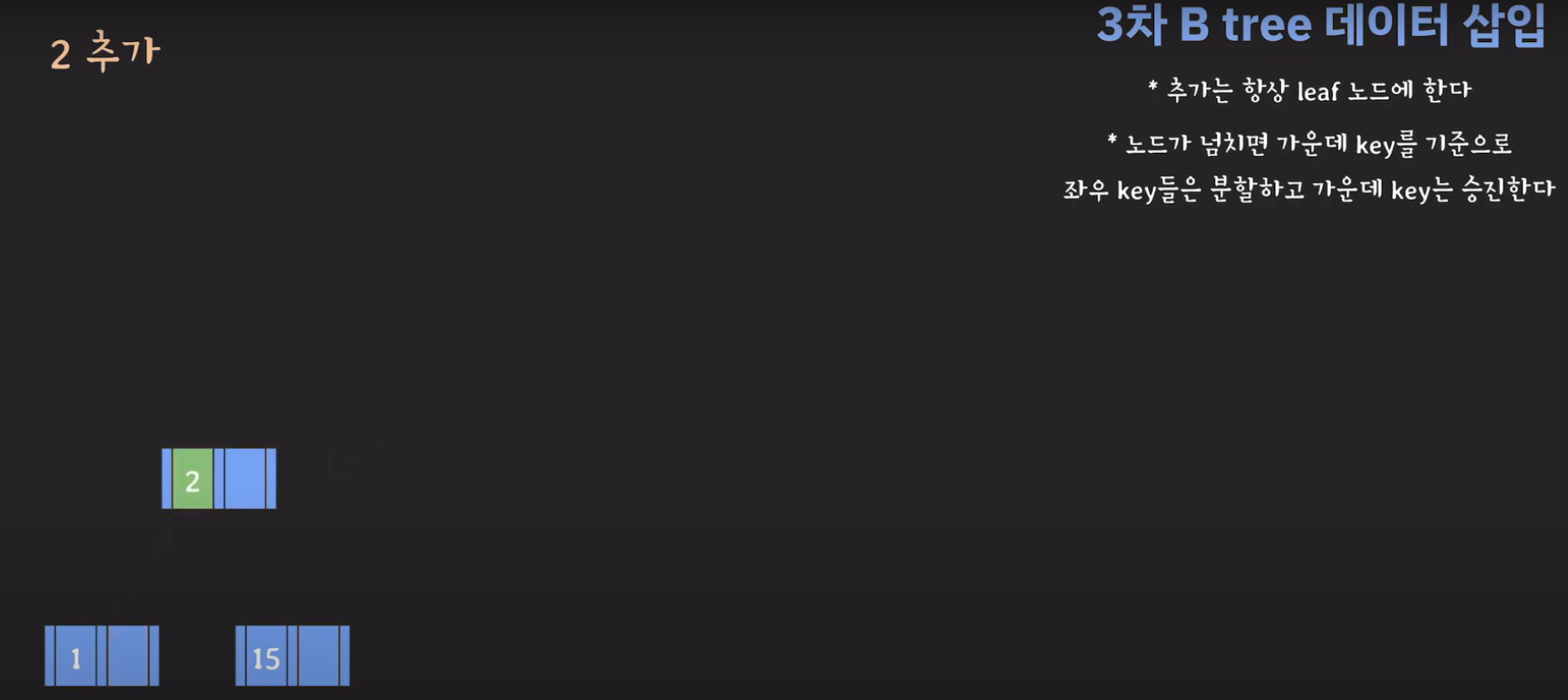
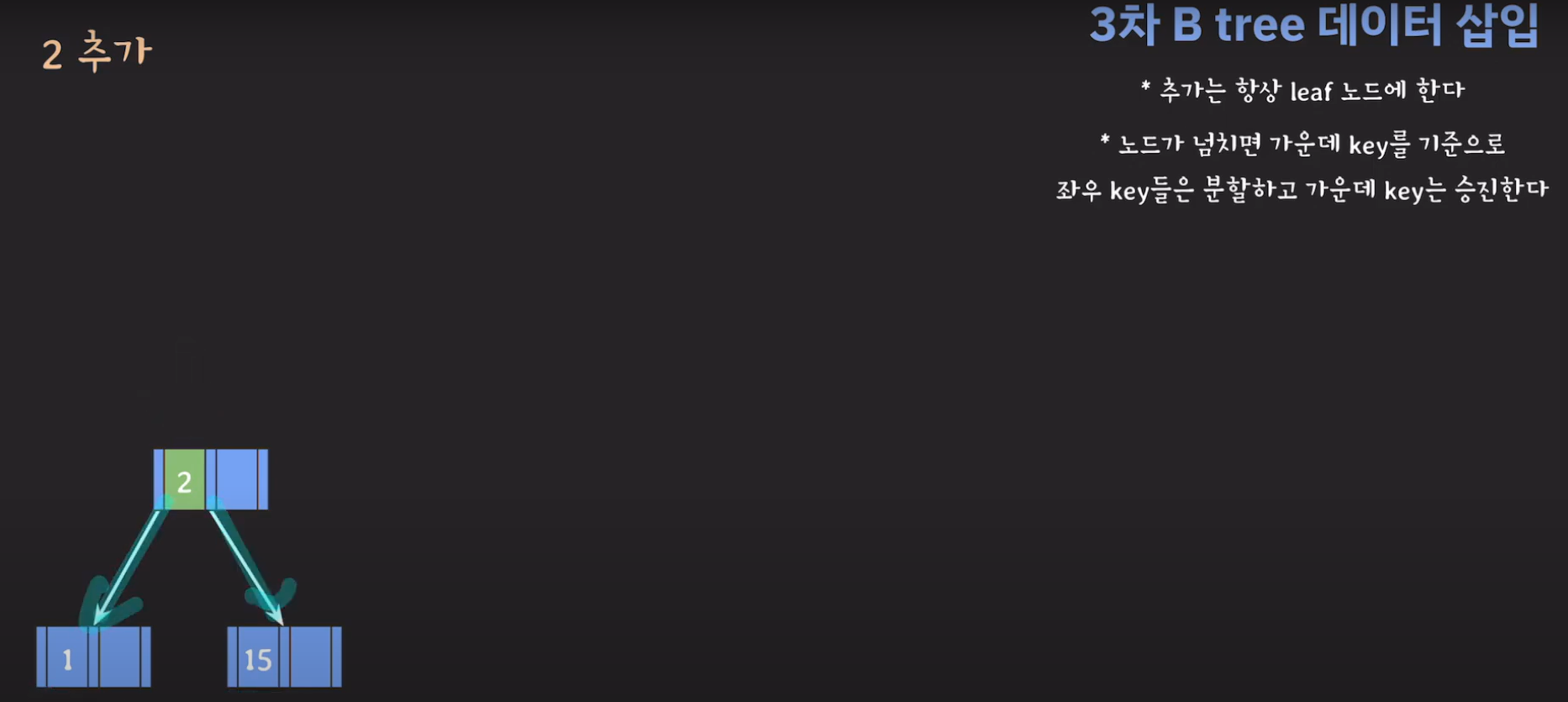

- 루트(2)와 비교해서 5가 더 크므로 오른쪽 서브 트리로 이동하고 오름차순으로 정렬해야 하므로 위와 같은 그림이 됩니다.

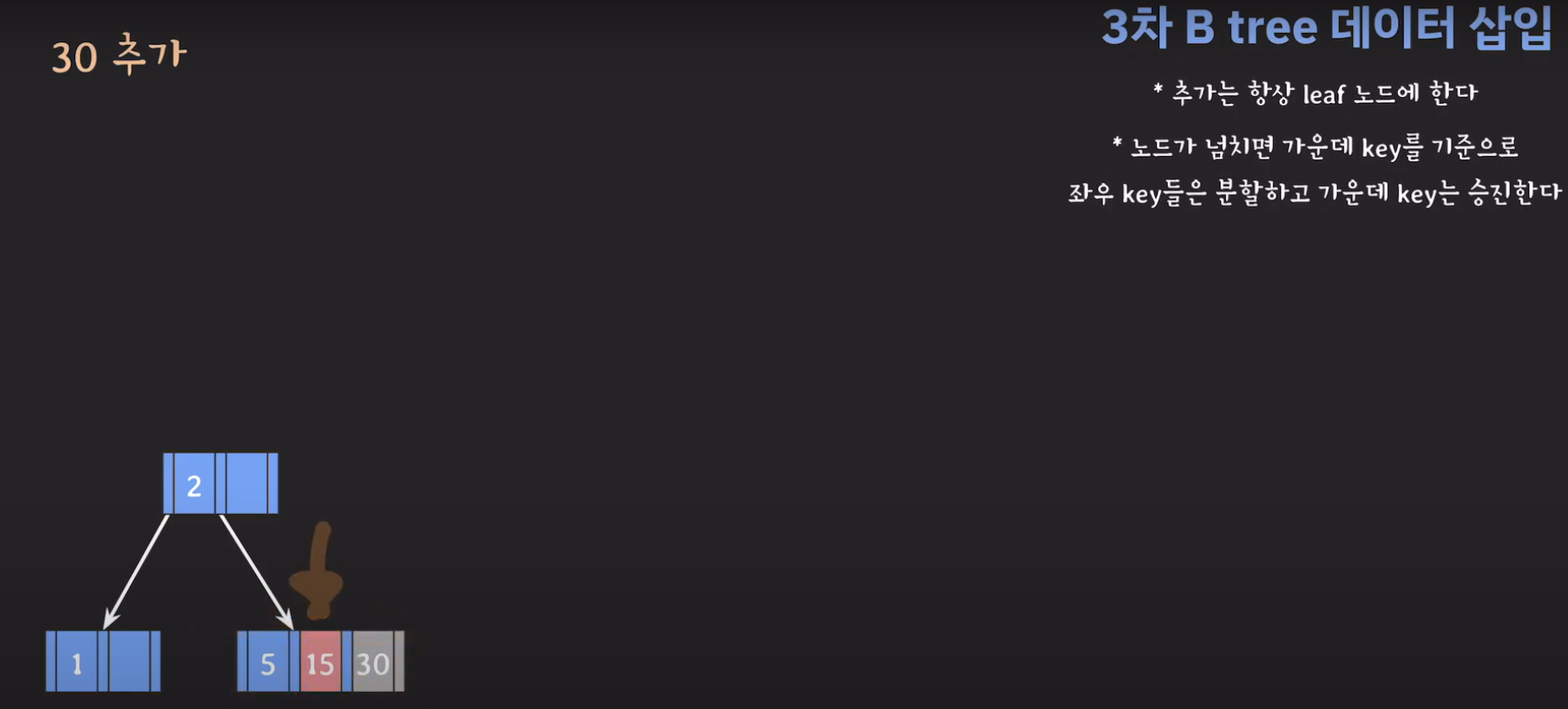
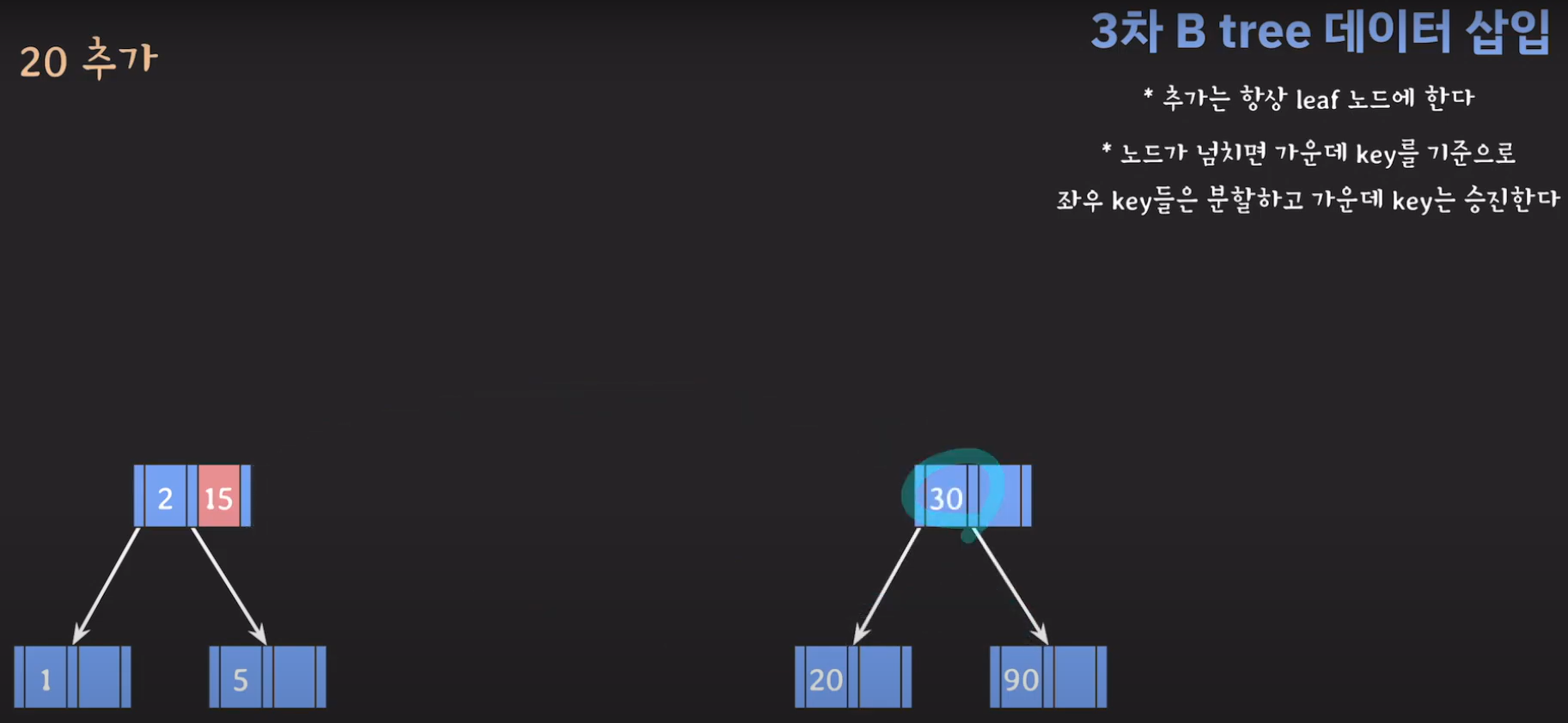
- 5와 30은 분할을 하고 15는 승진해야 합니다.
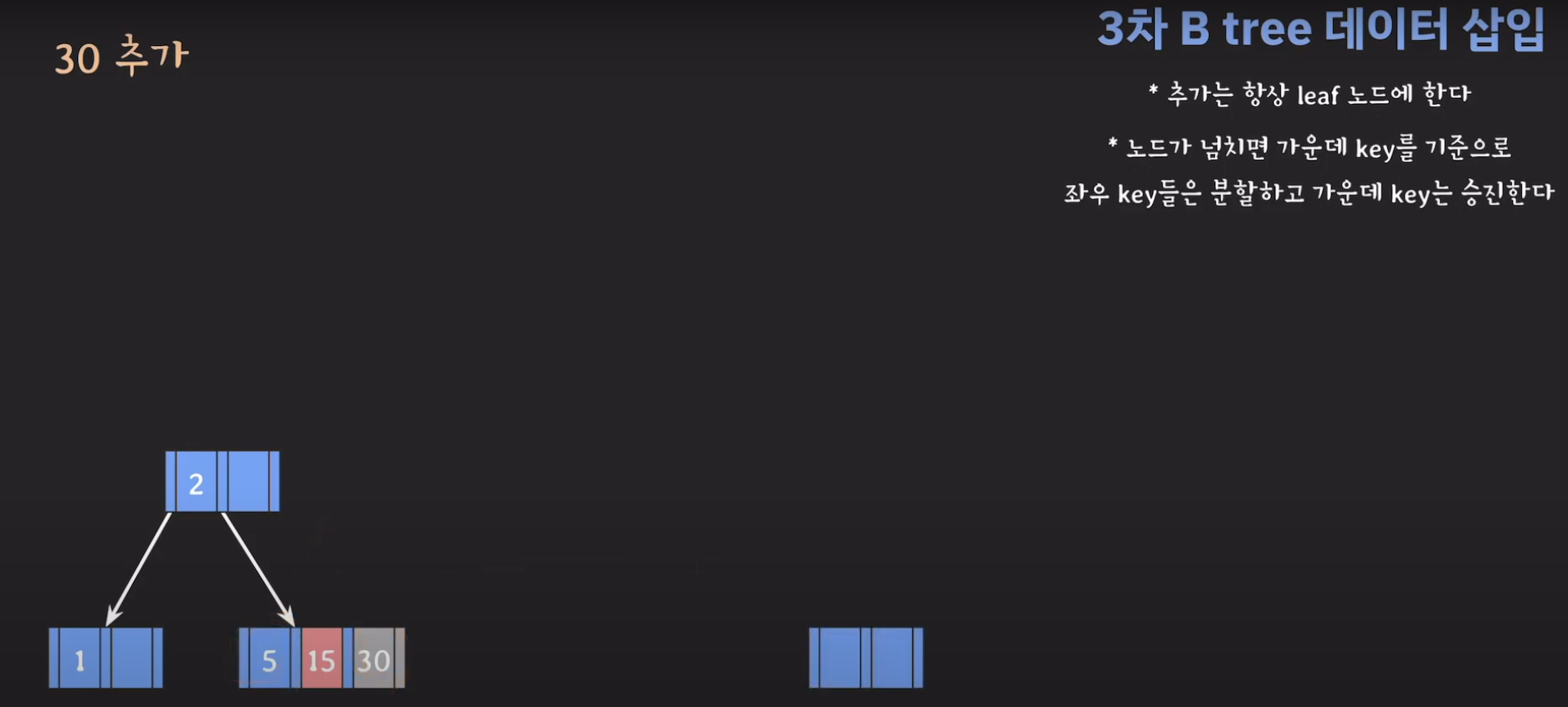
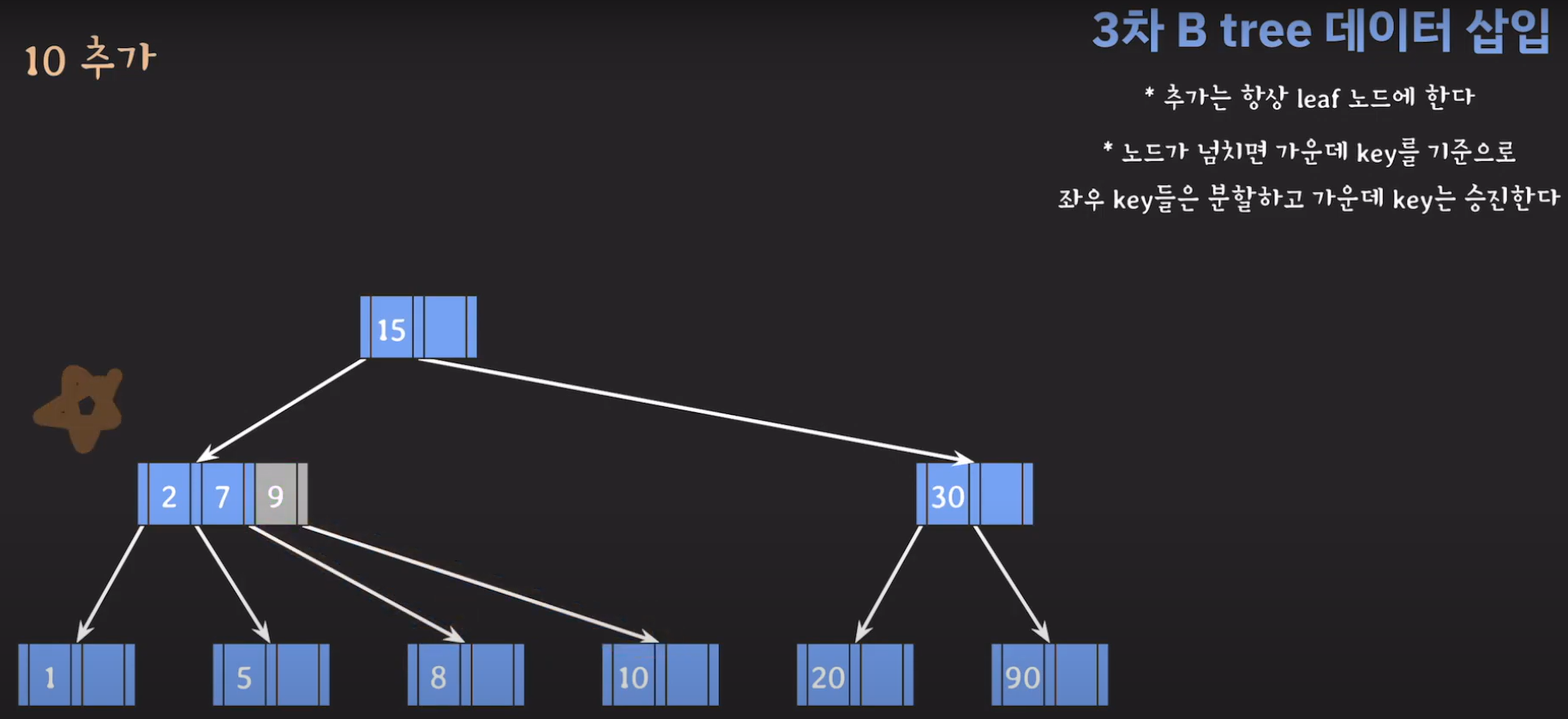
- 분할하기 위해서 새로운 노드를 만듭니다.
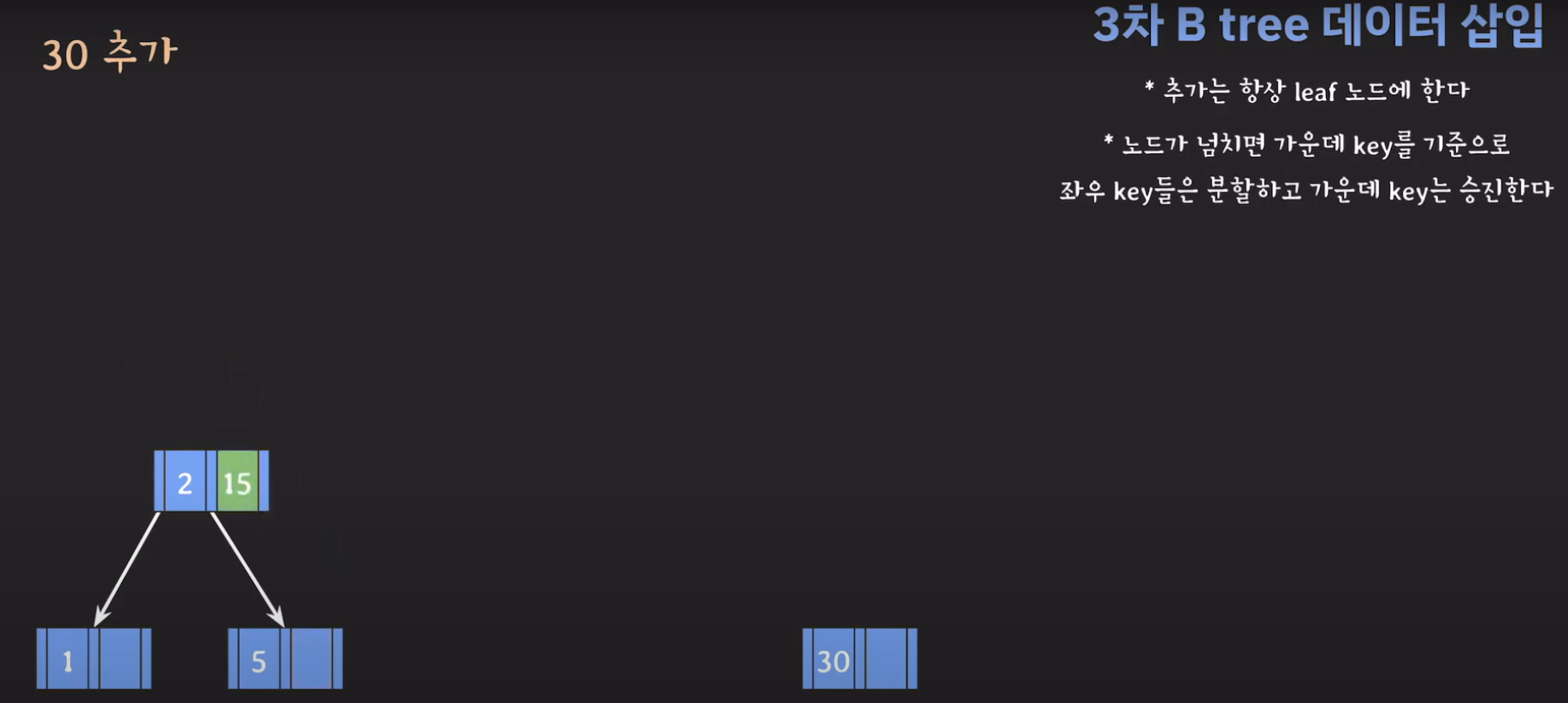
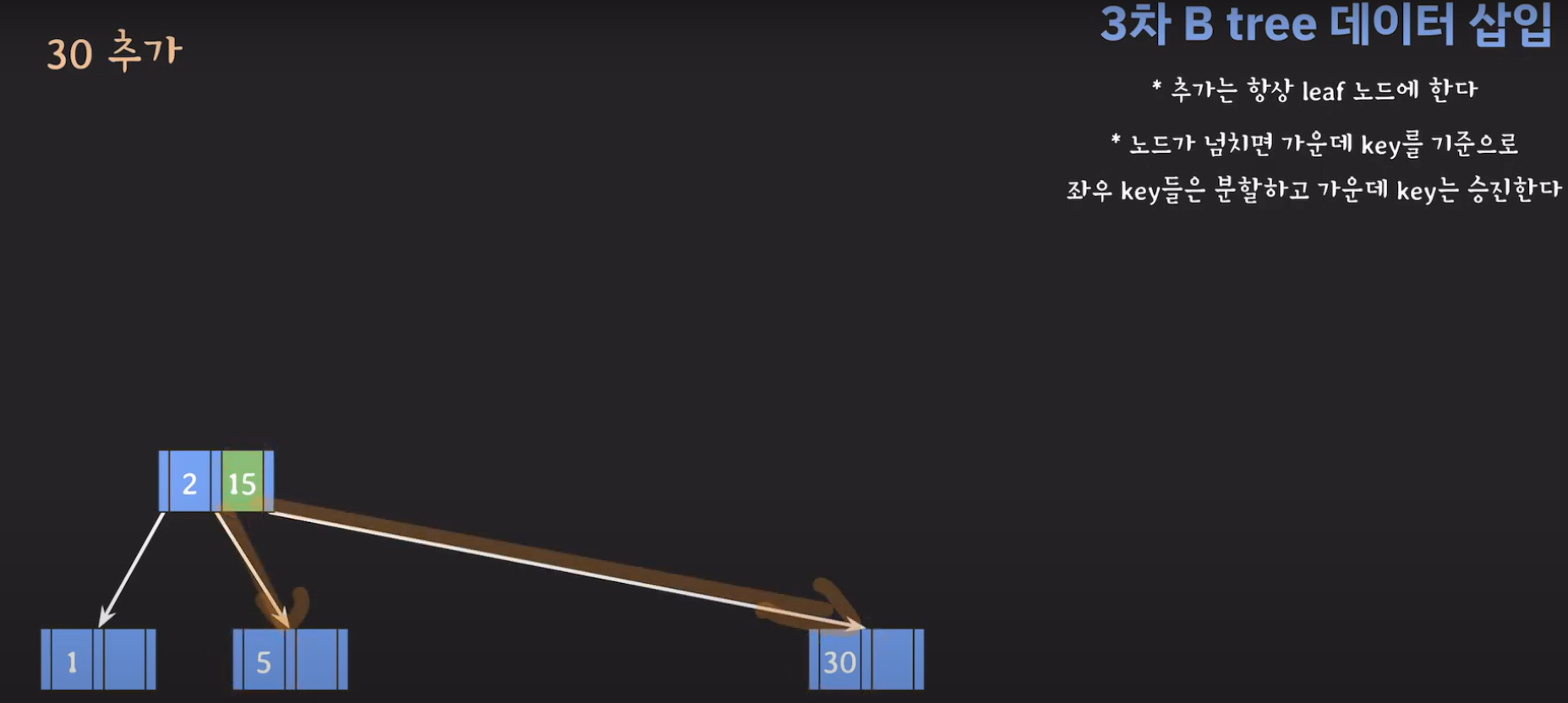
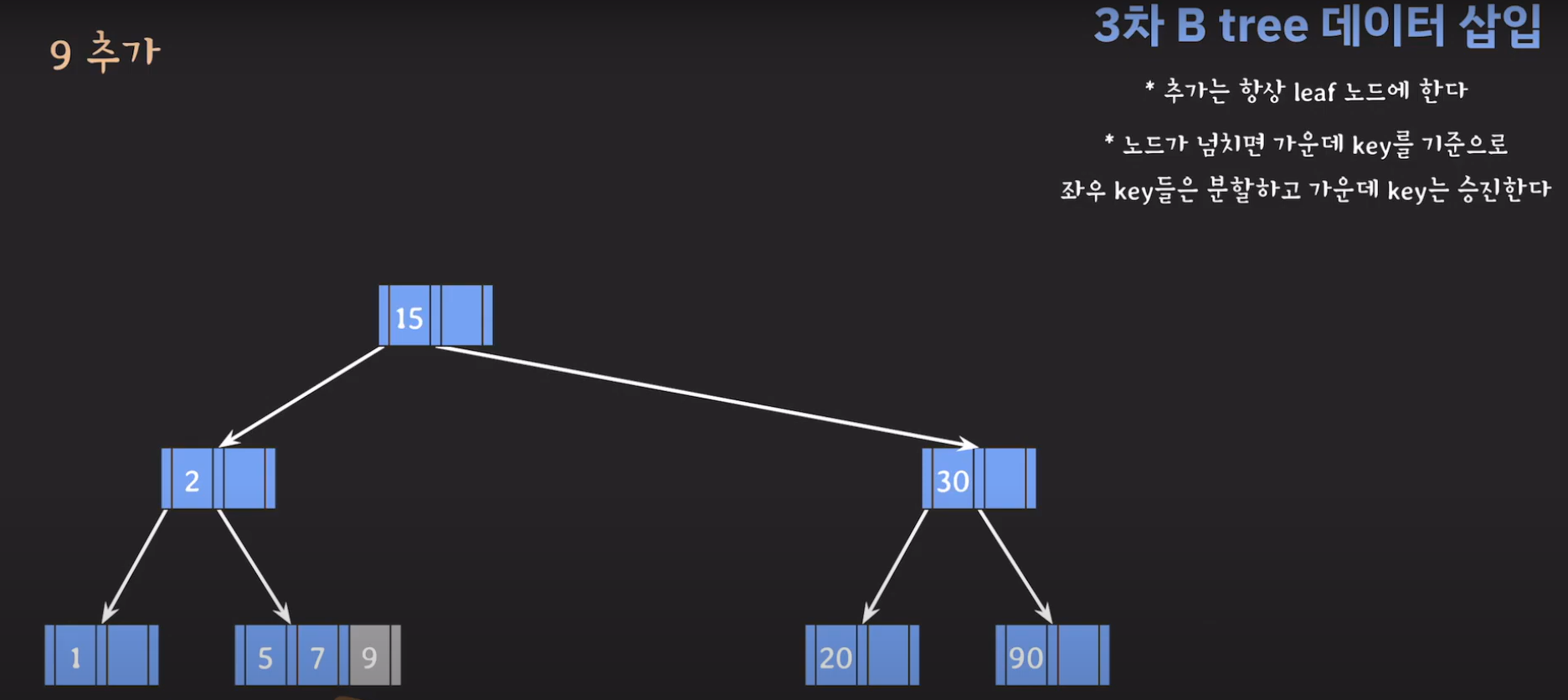
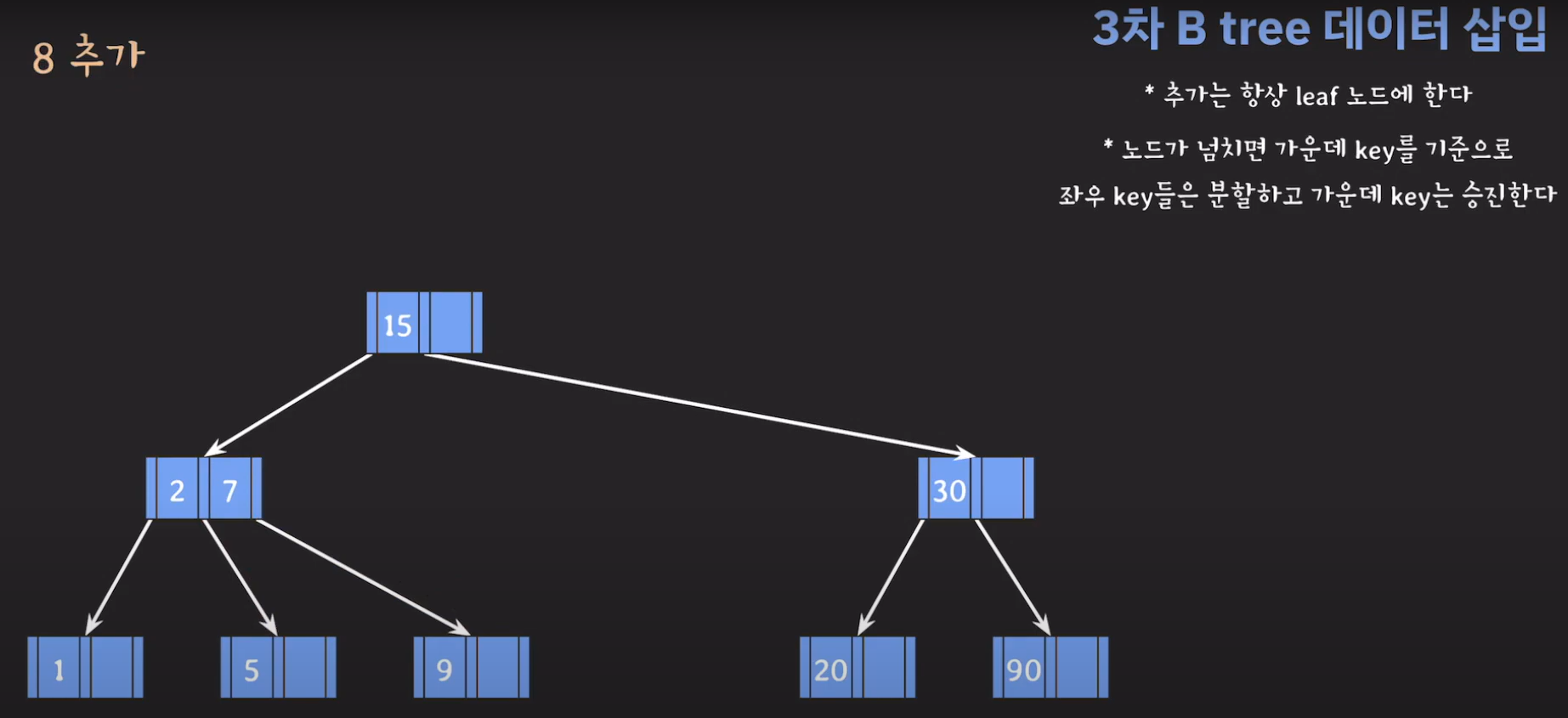
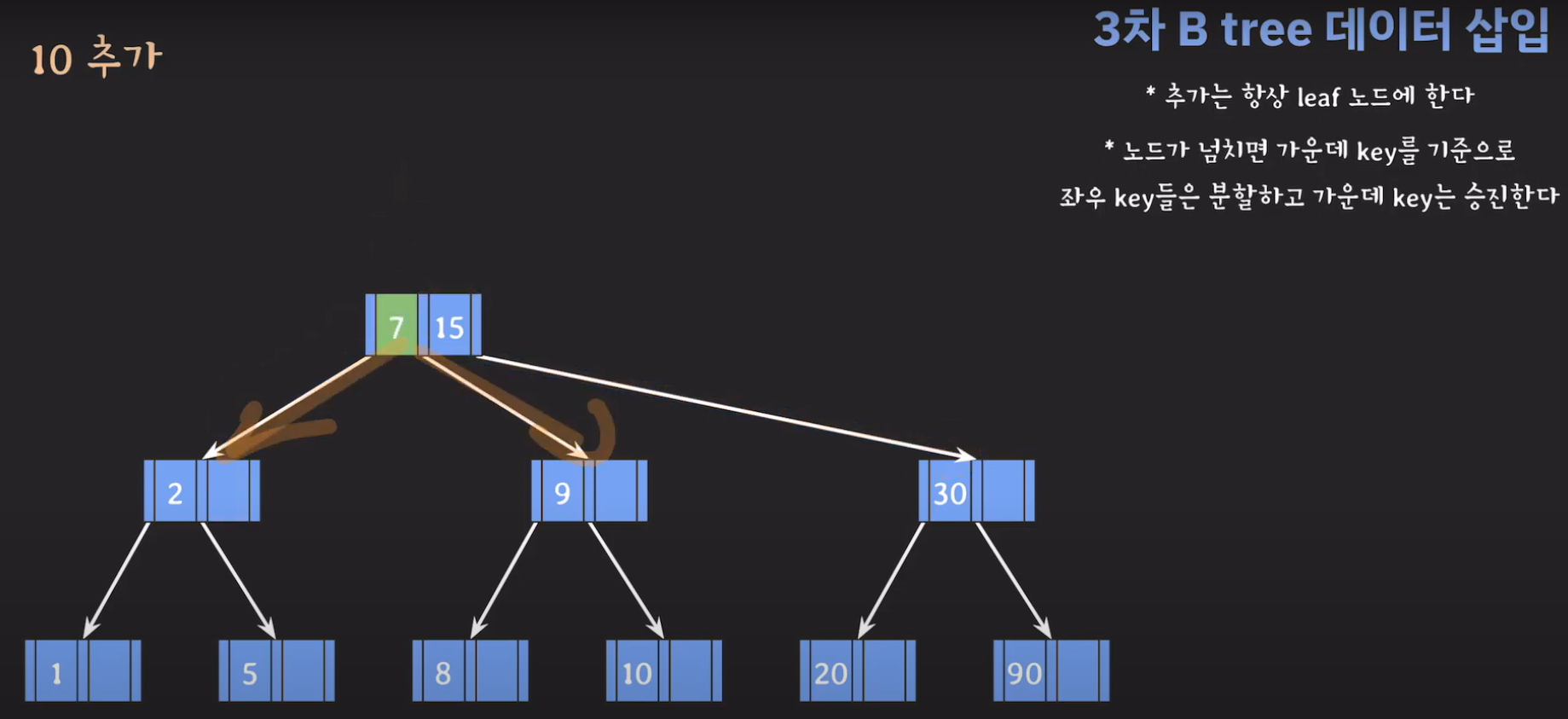
- 루트부터 비교해서 리프노드에 공간이 있다면 오름차순으로 데이터를 삽입시켜 줍니다.

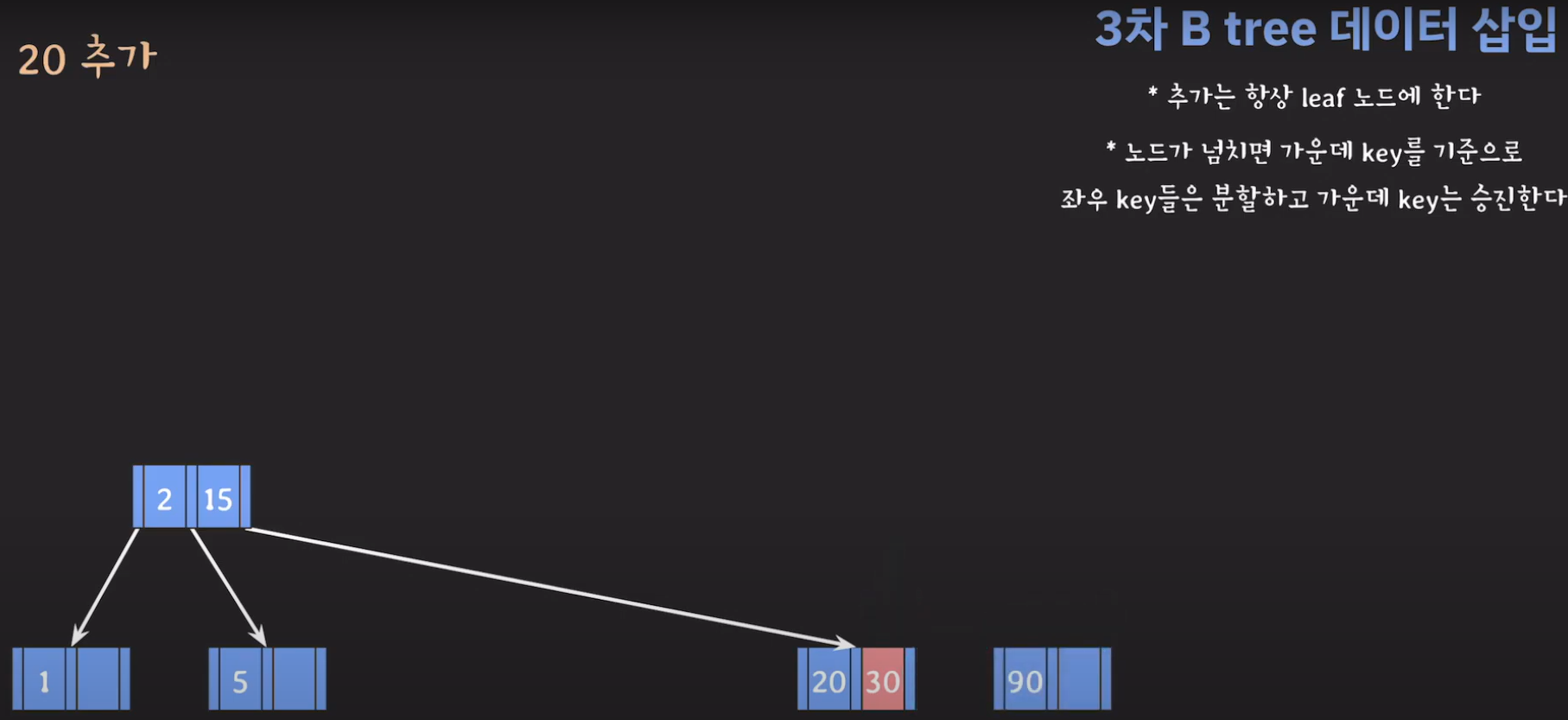
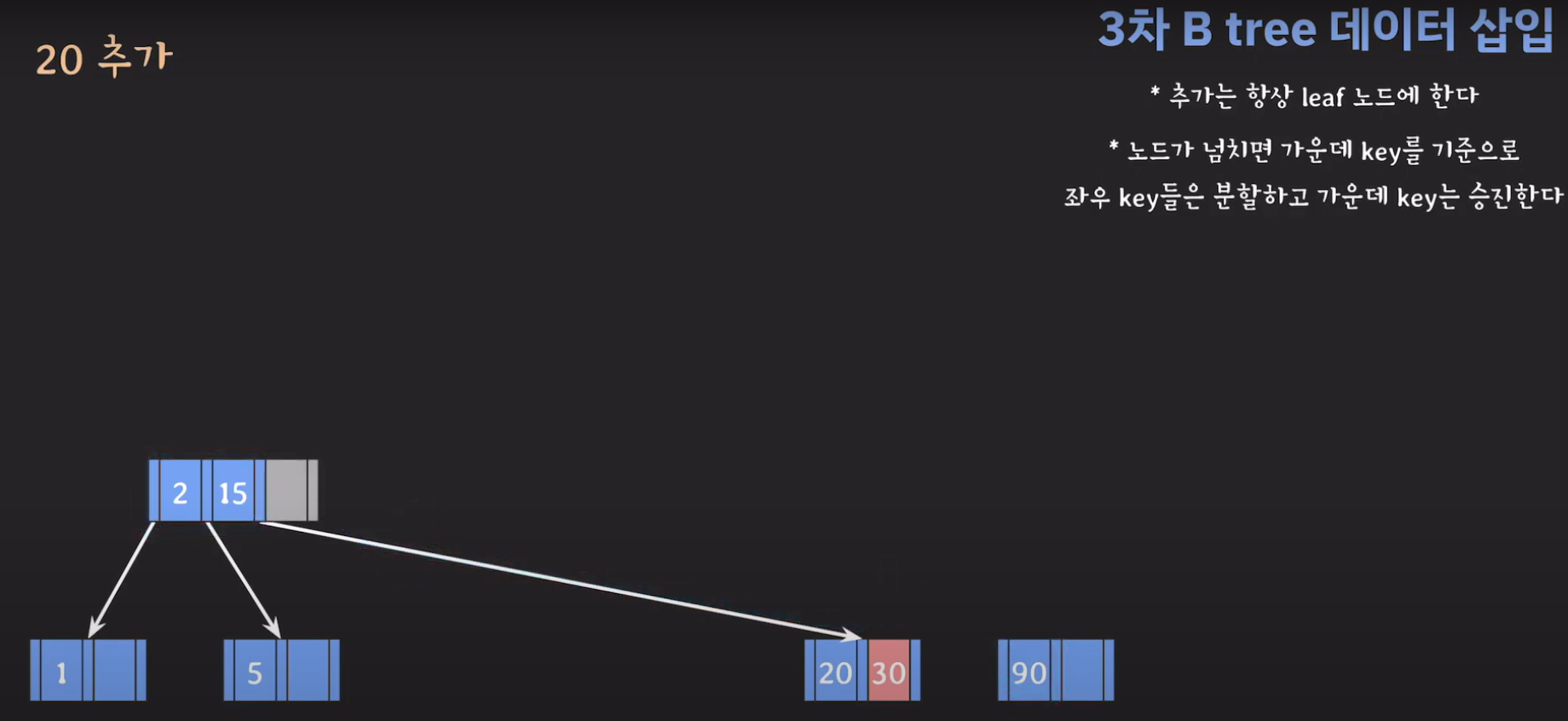
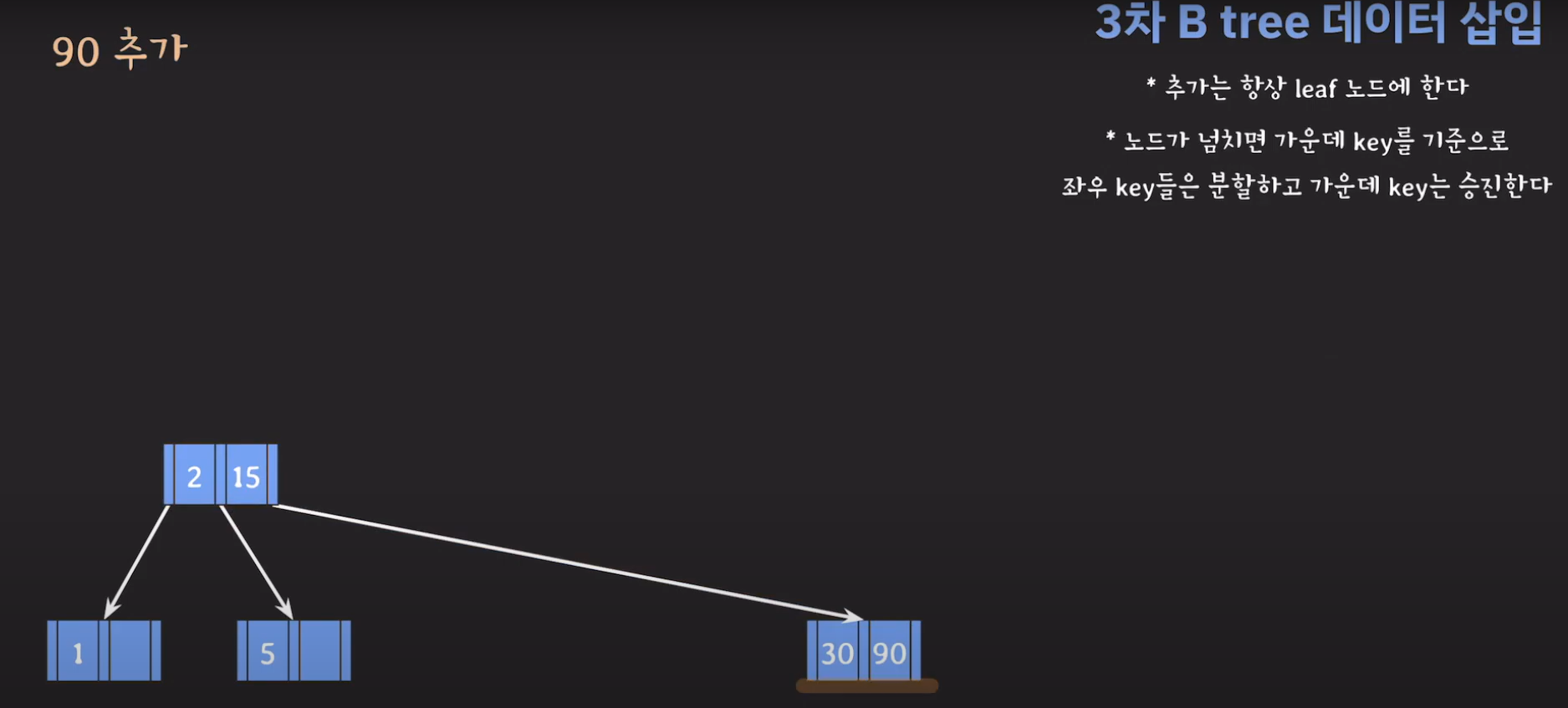
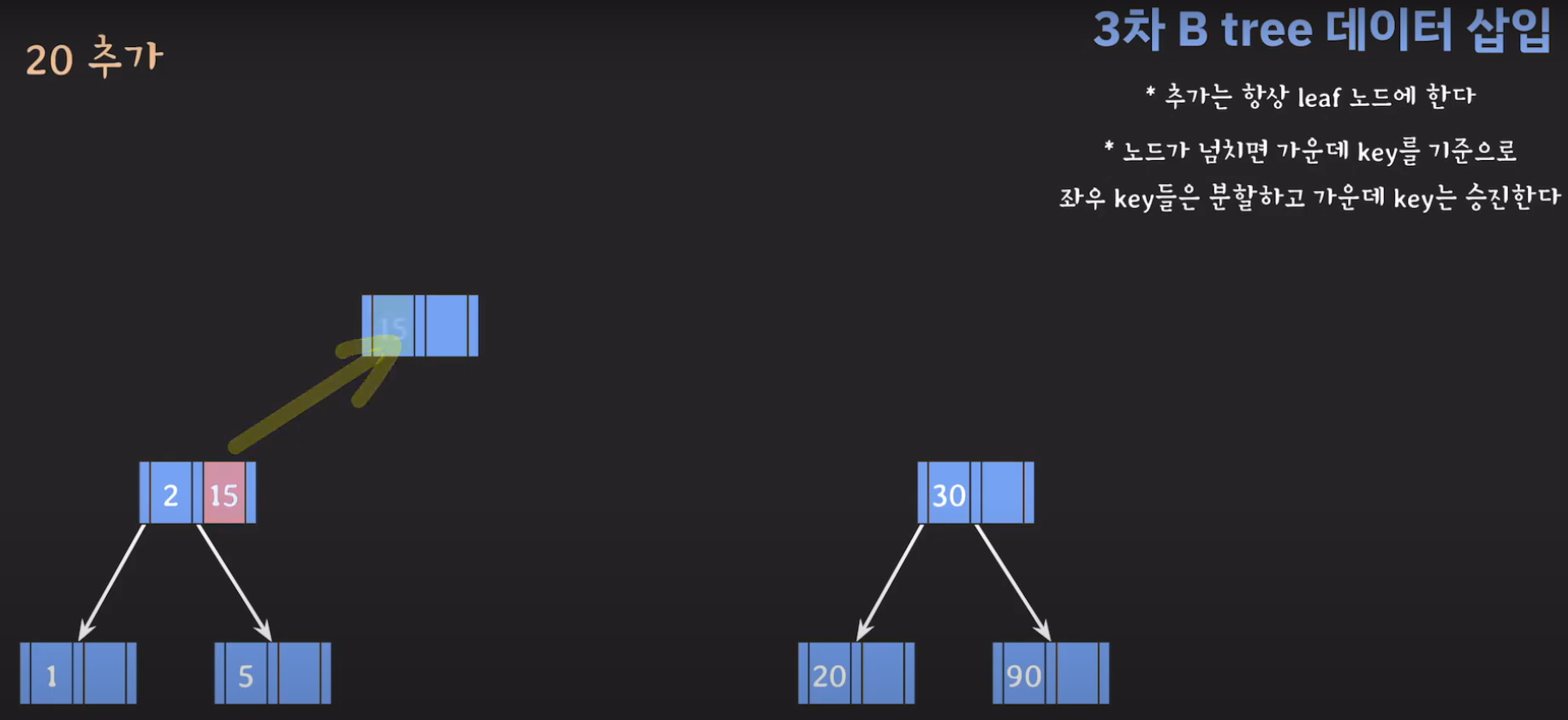
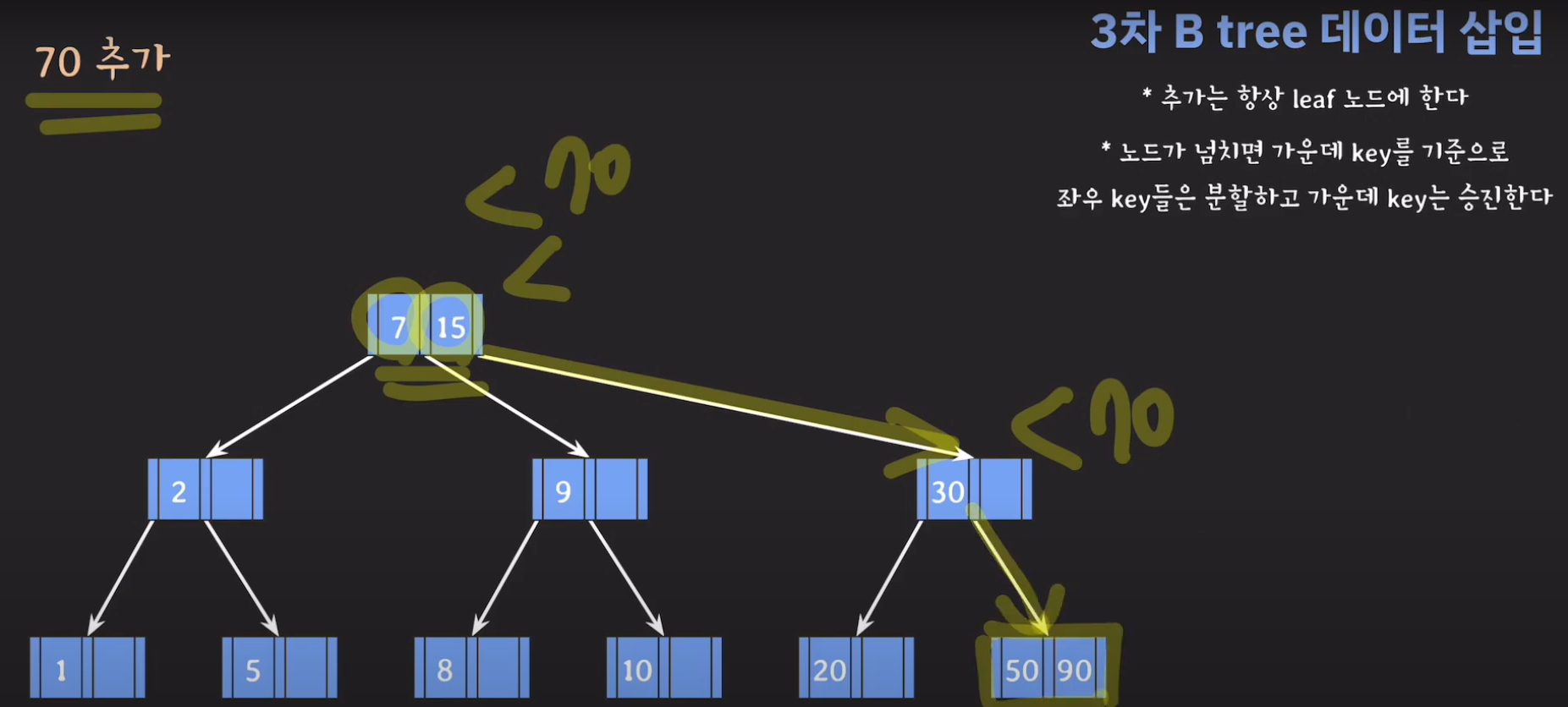
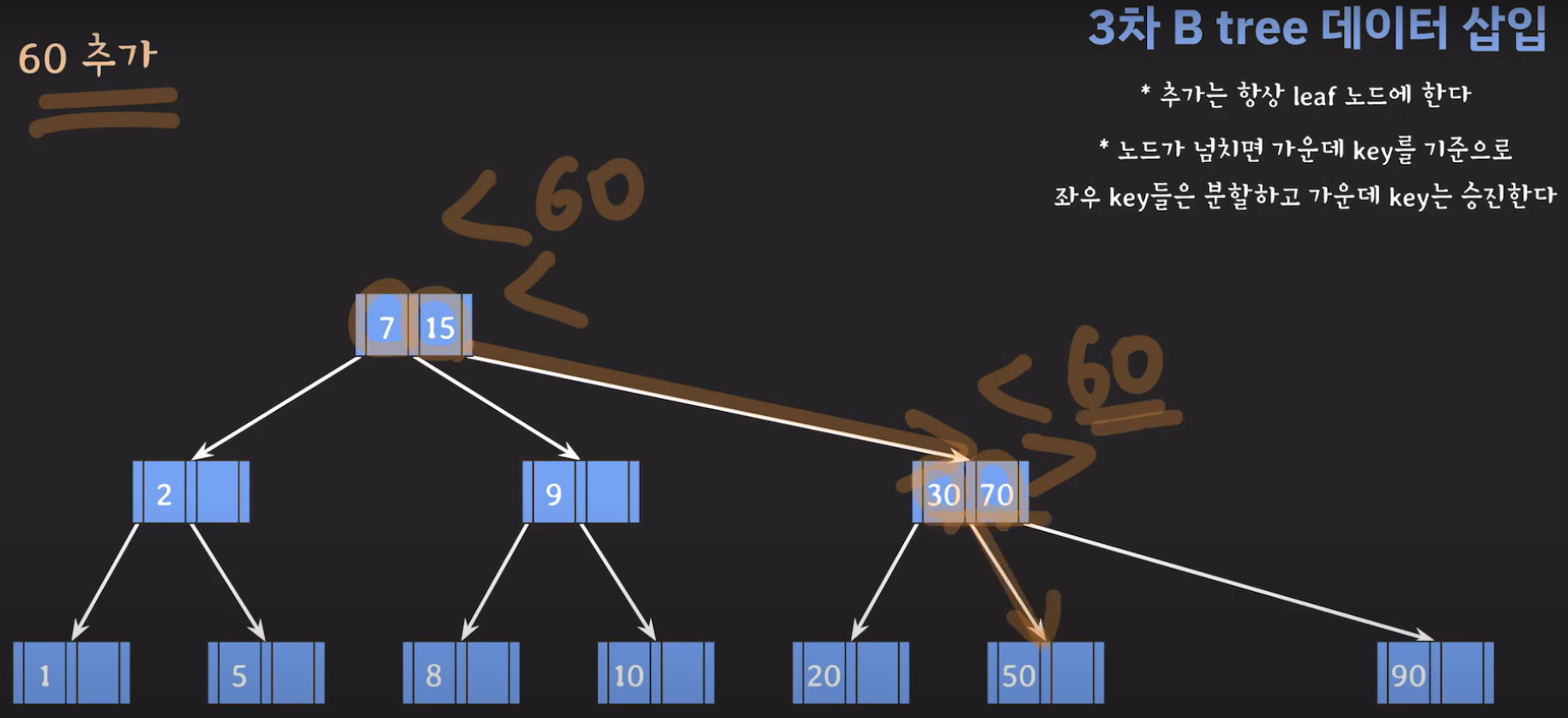
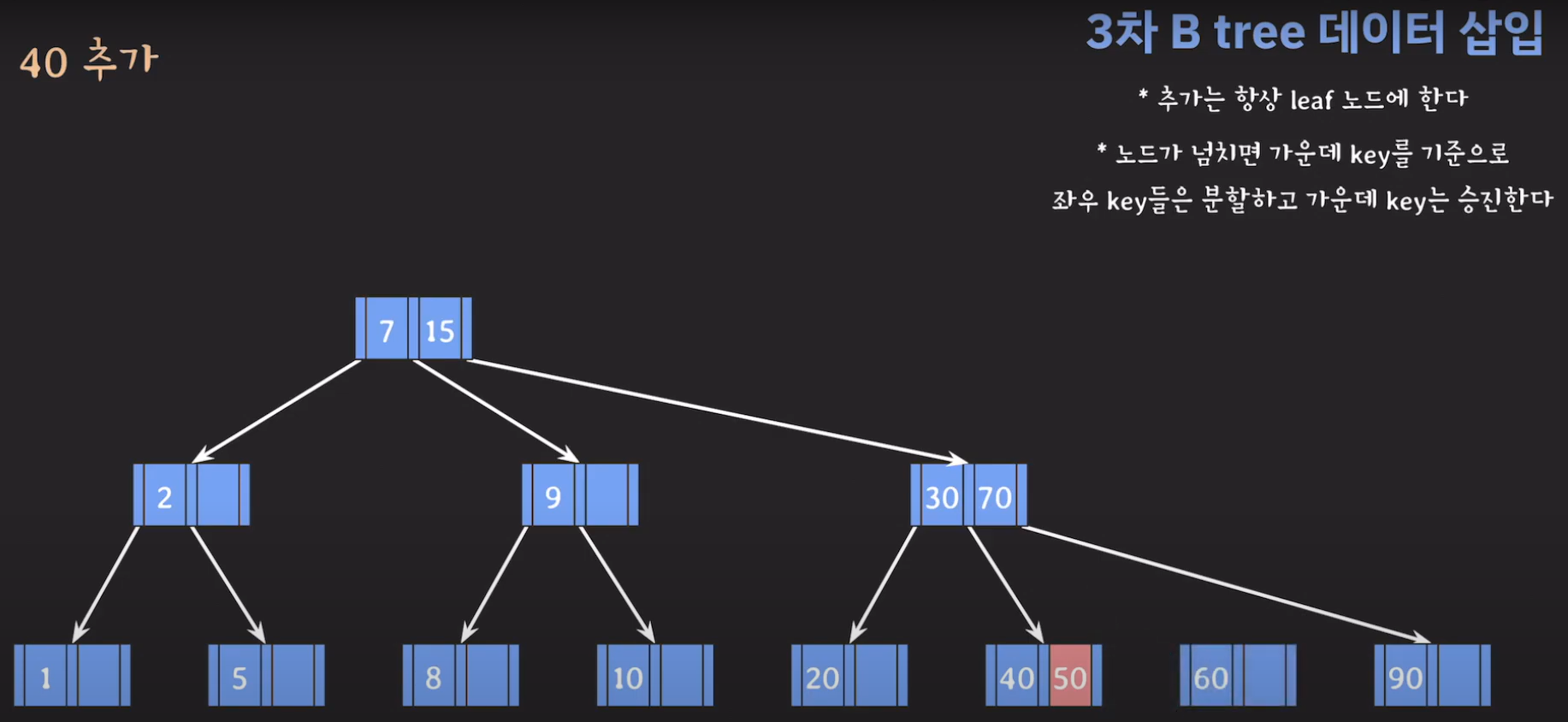
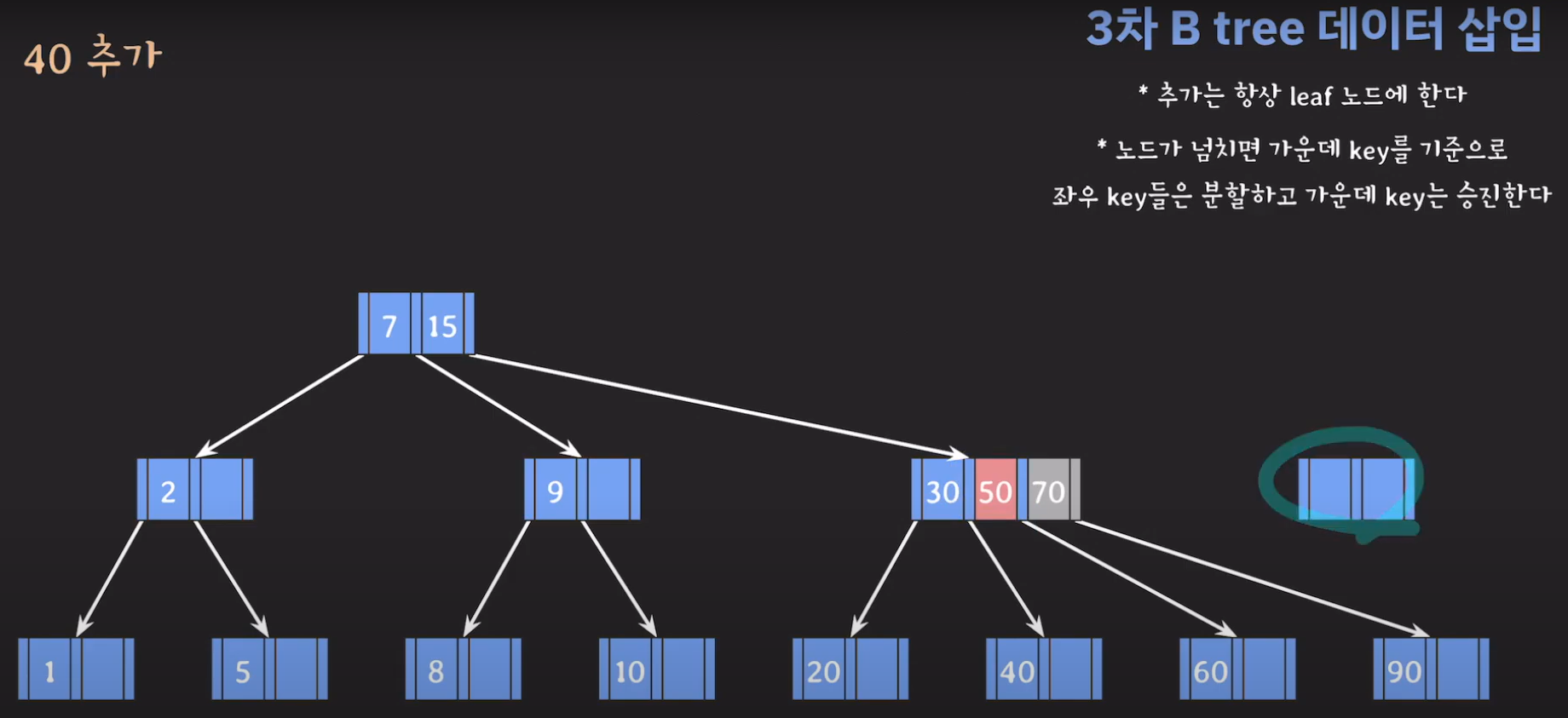
- 30을 승진시켜야 하는데 부모 노드가 꽉 찼으므로 추가 공간을 만들어줍니다.
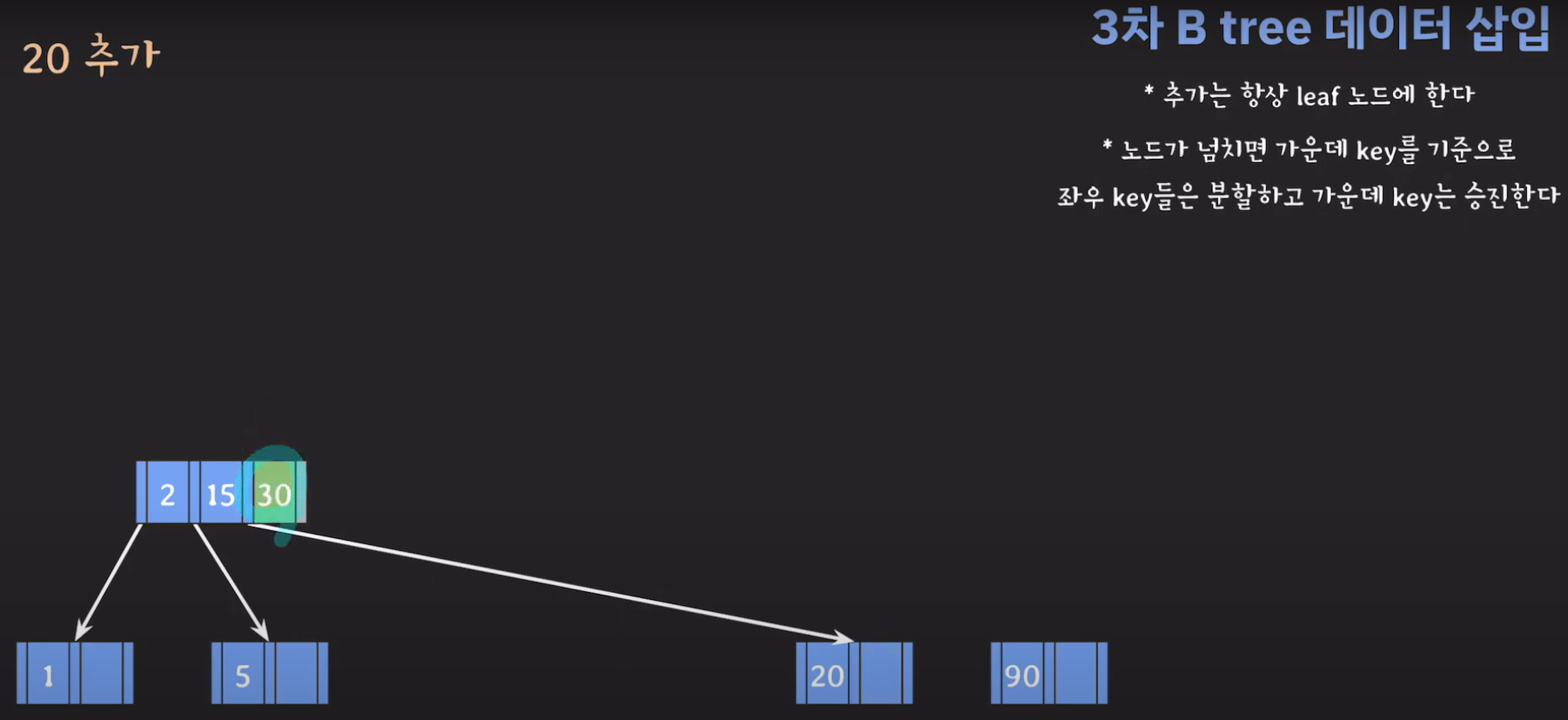
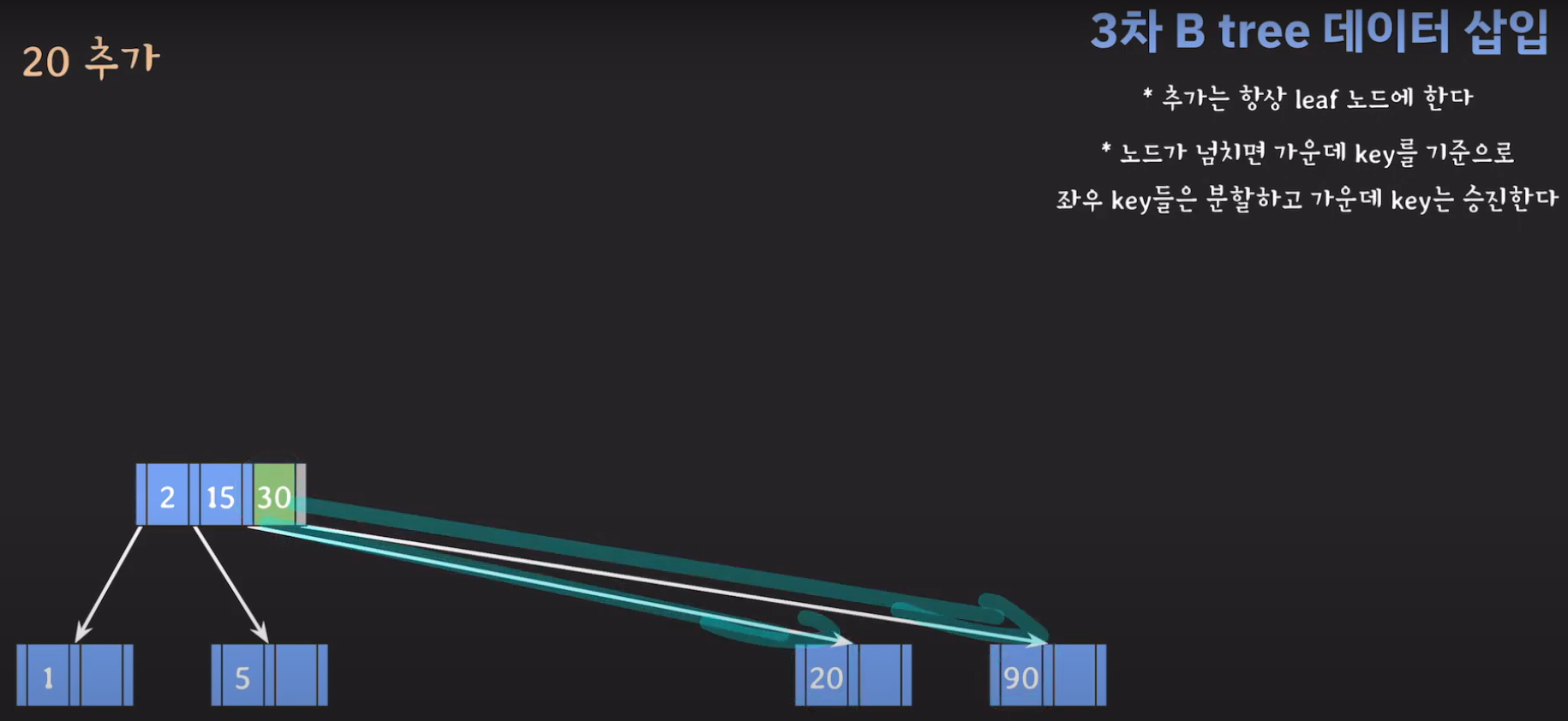
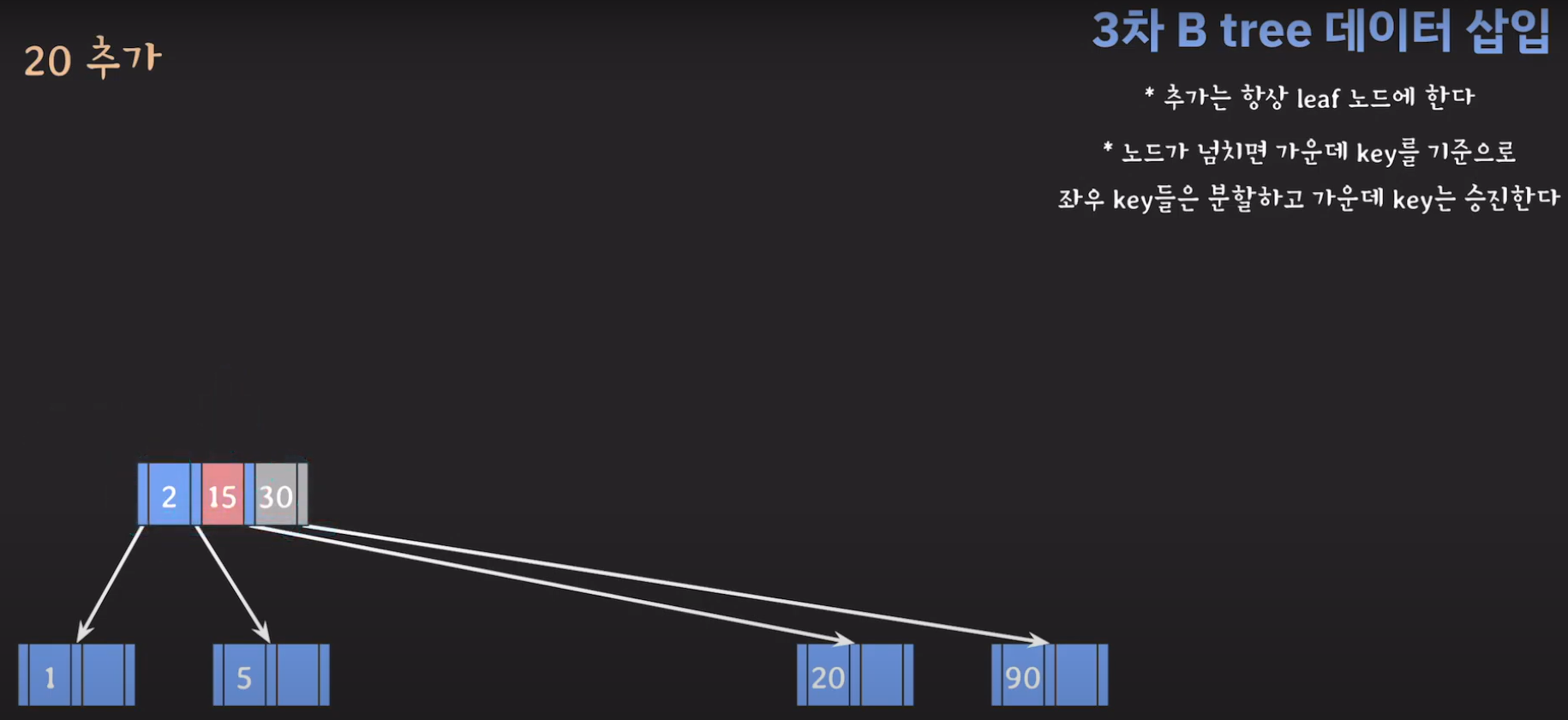
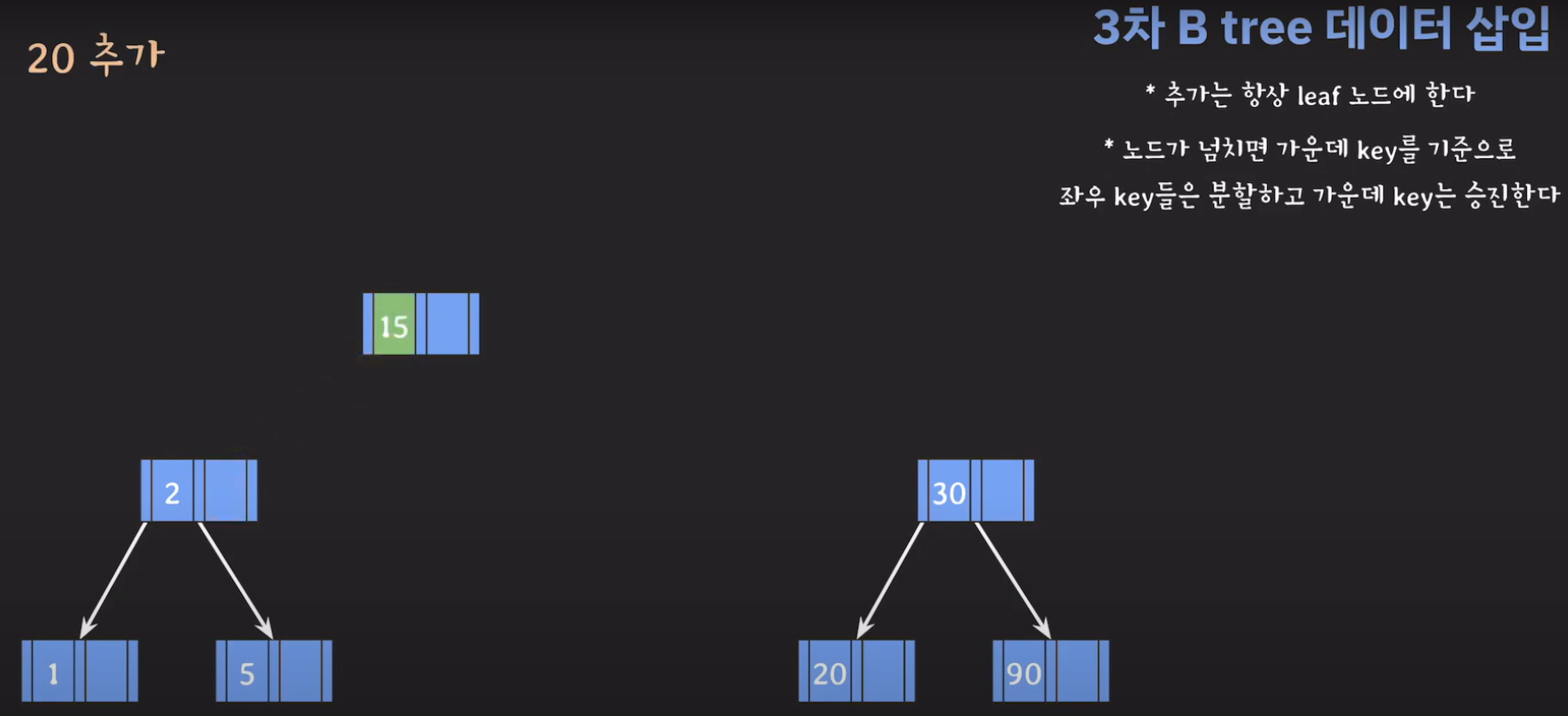
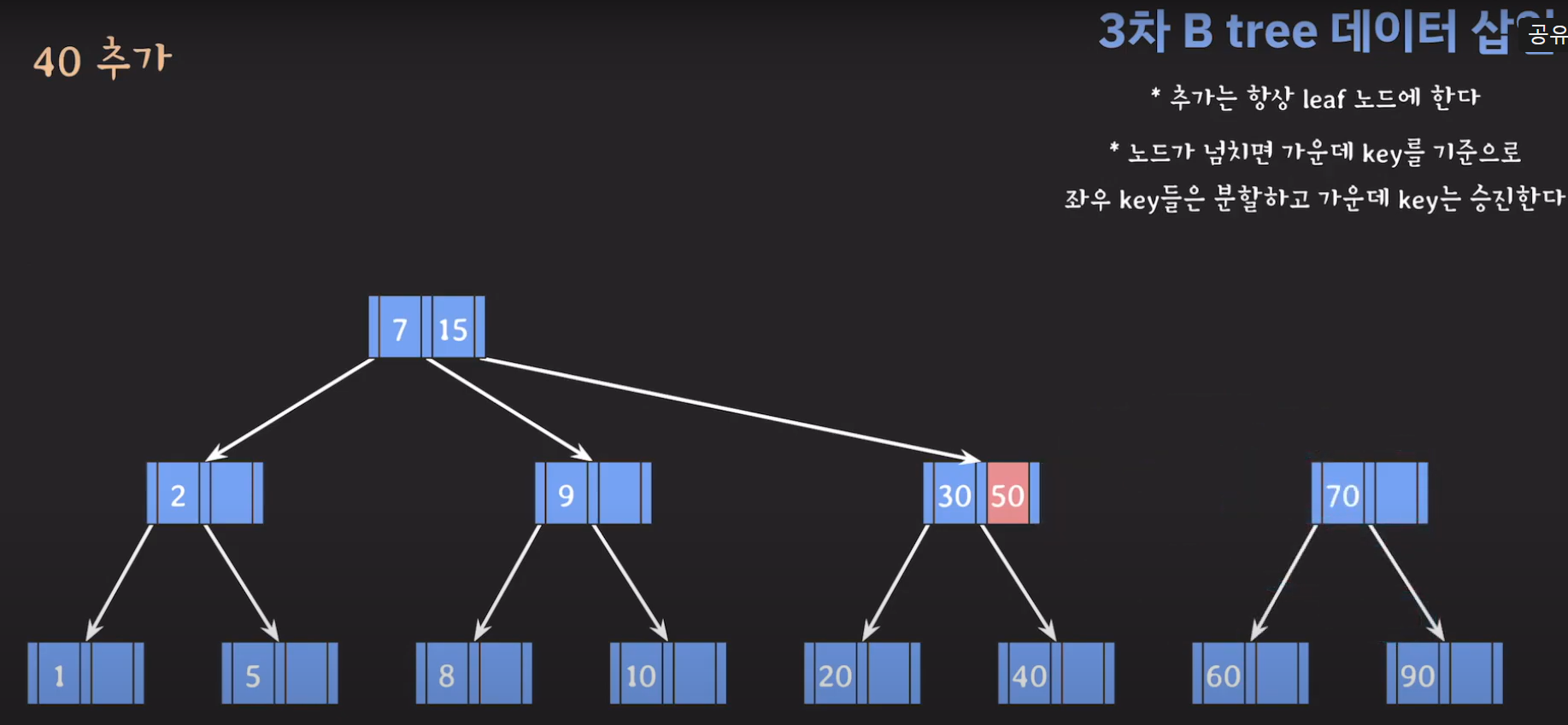
- 부모 노드도 꽉 찼으므로 가운데 값을 승진시키고 두 값을 분할하면 됩니다.
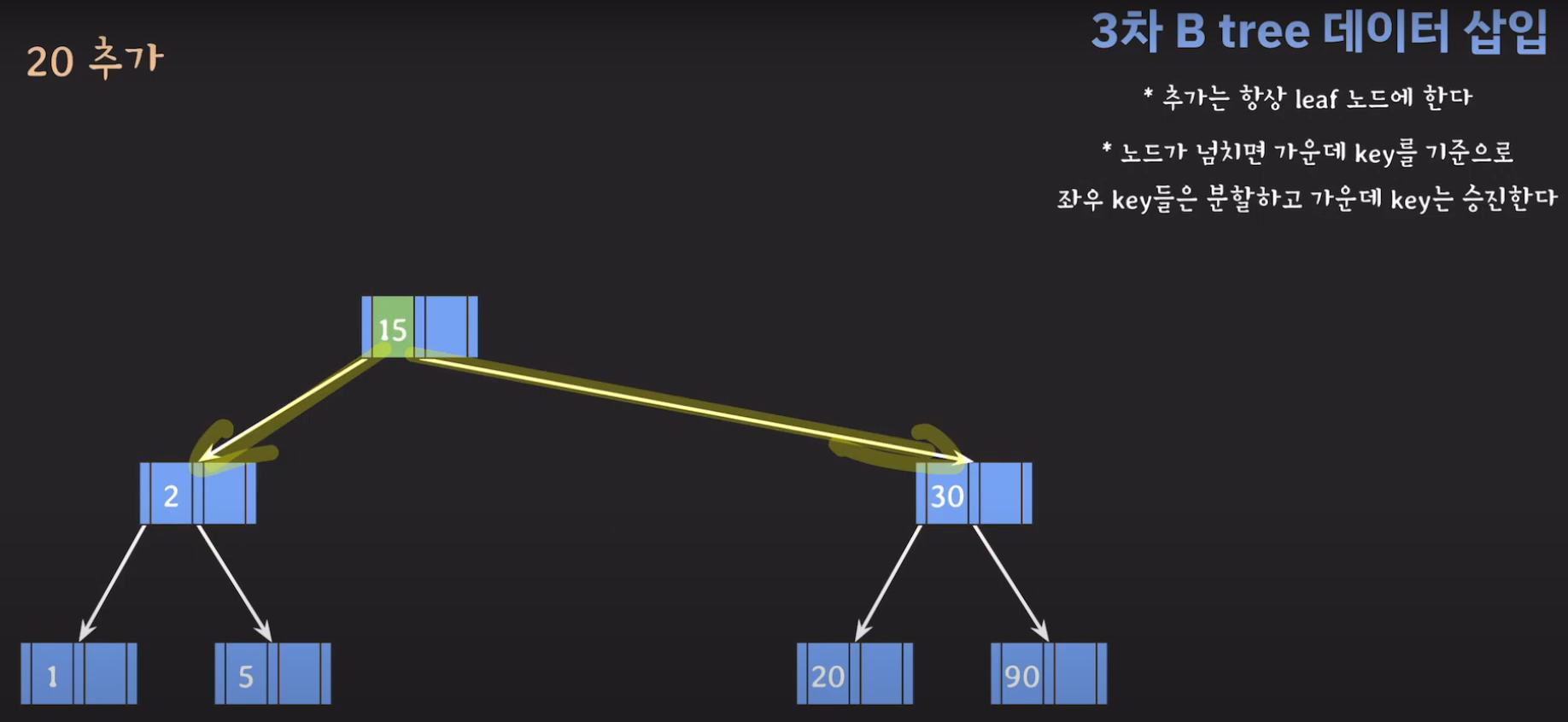
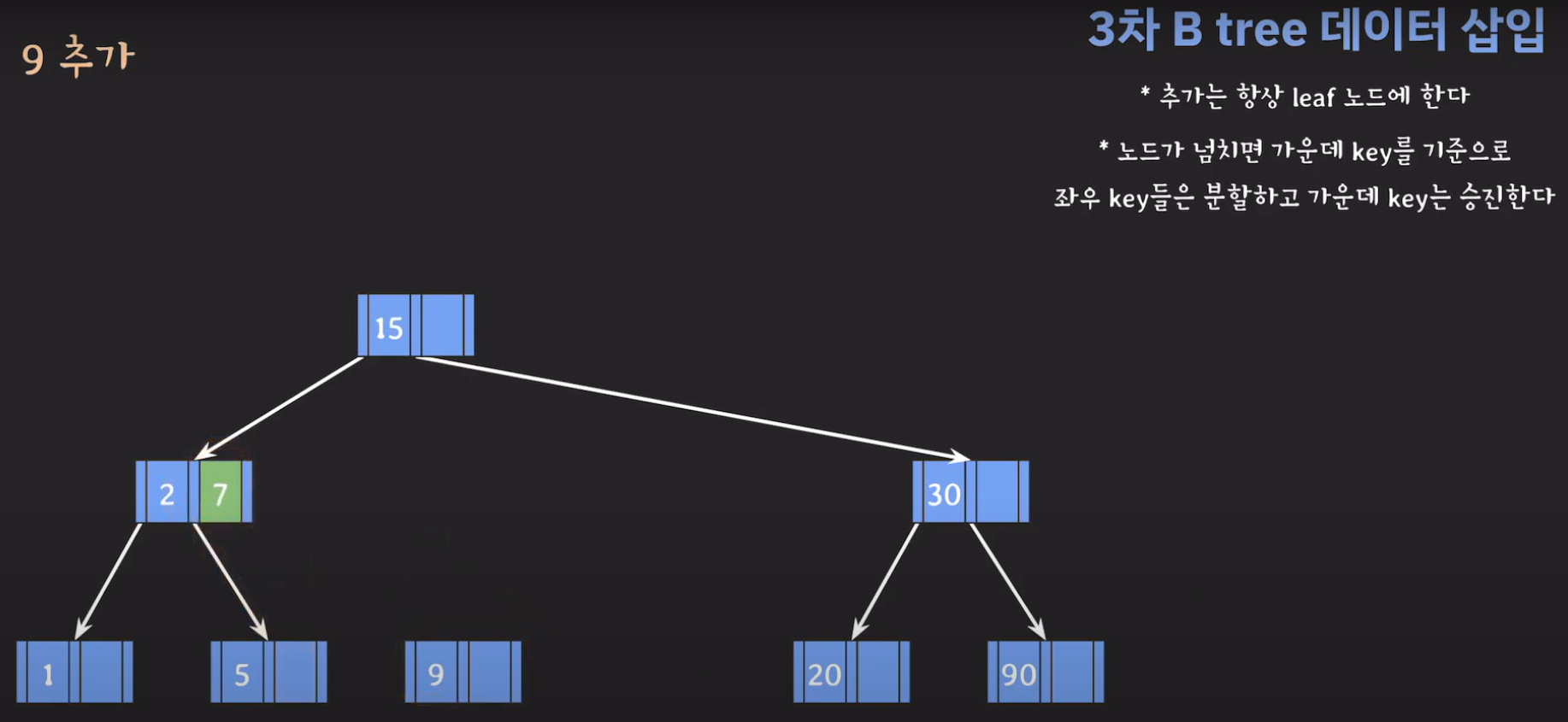
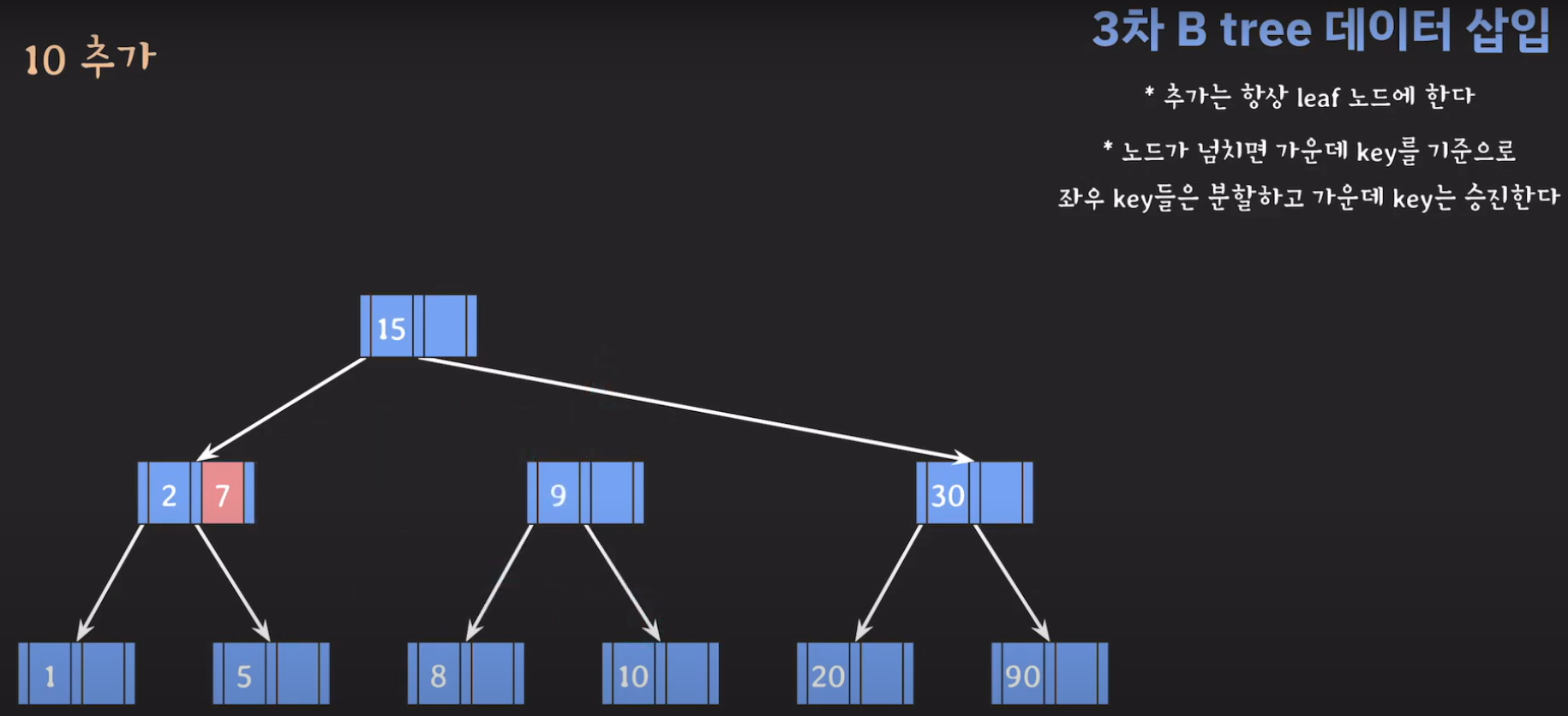
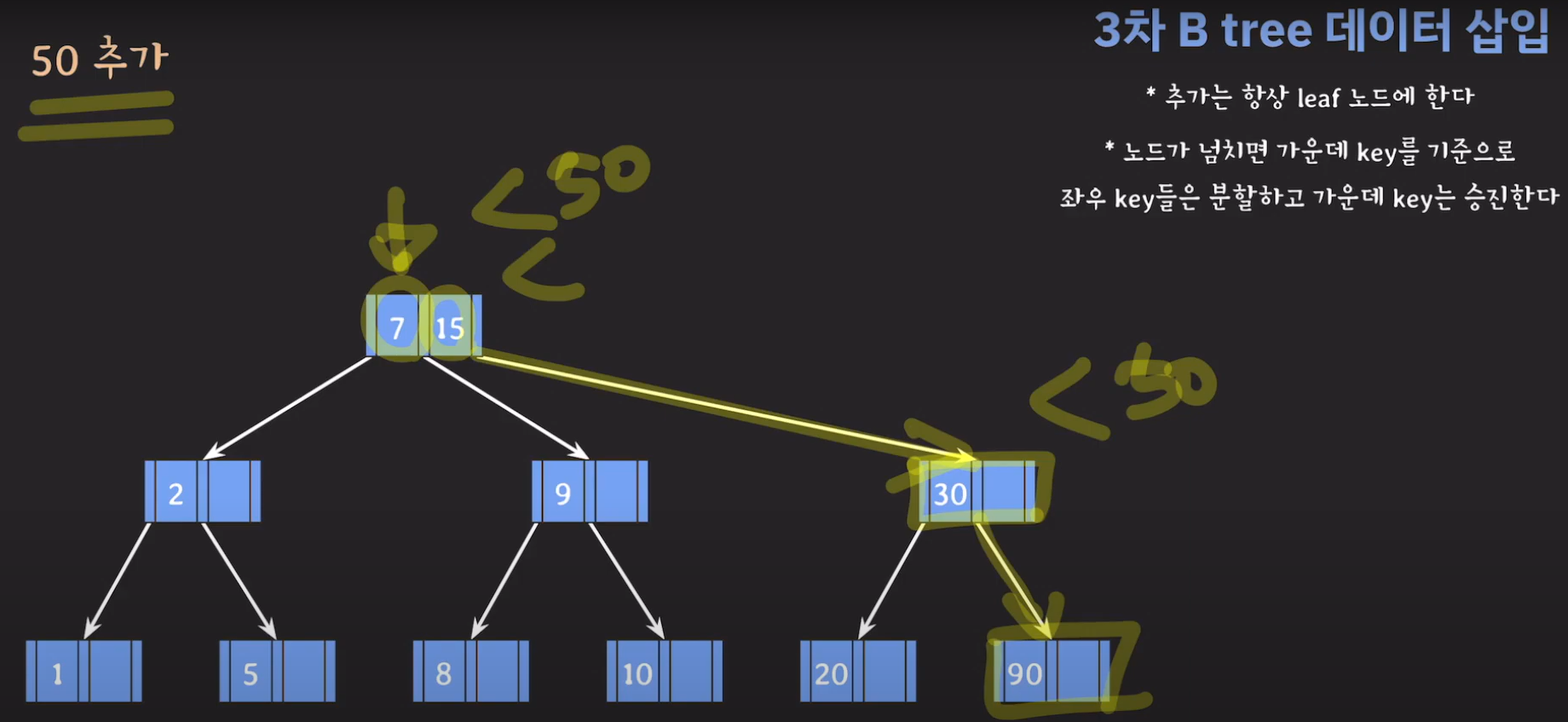
- 오름차순으로 정렬해야 하니까 15를 먼저 옮겨 줍시다.
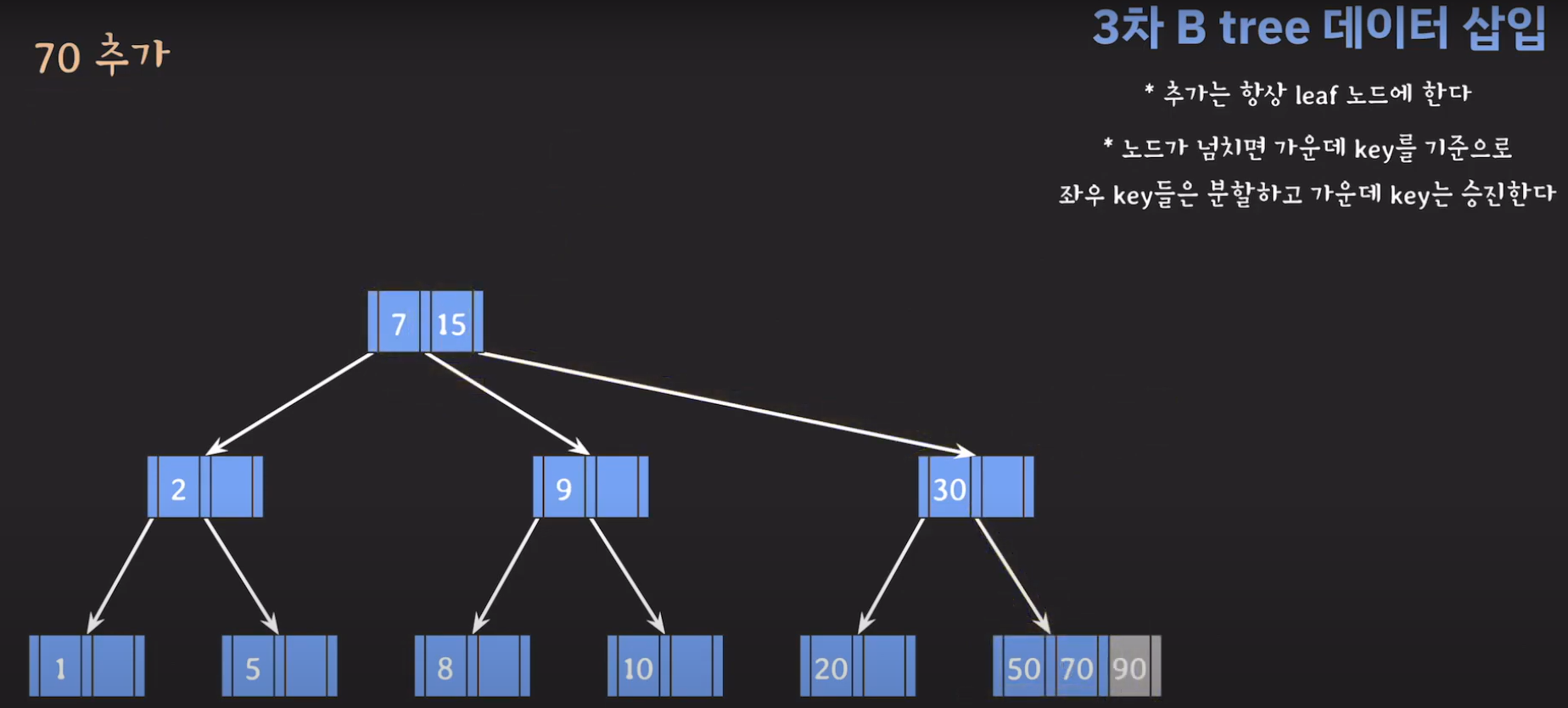
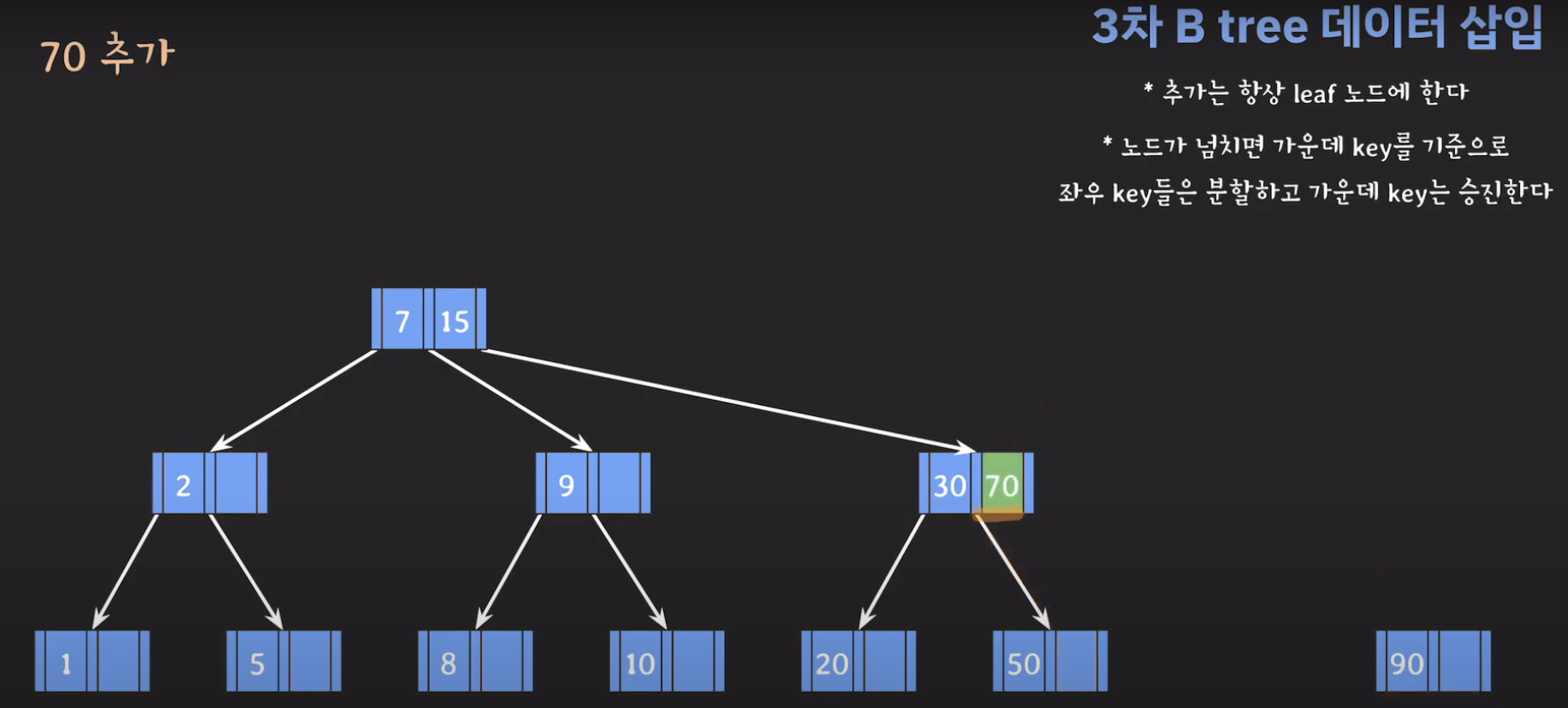
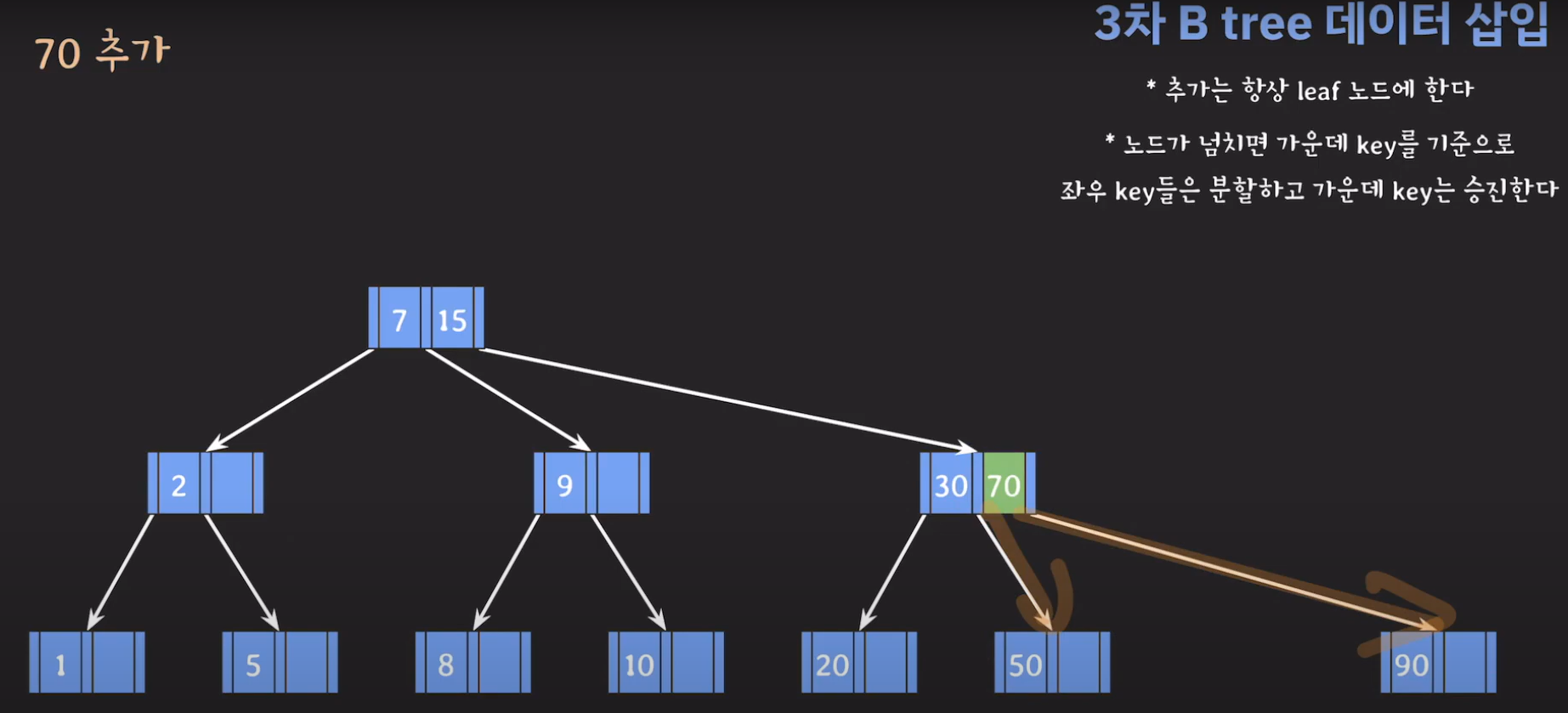
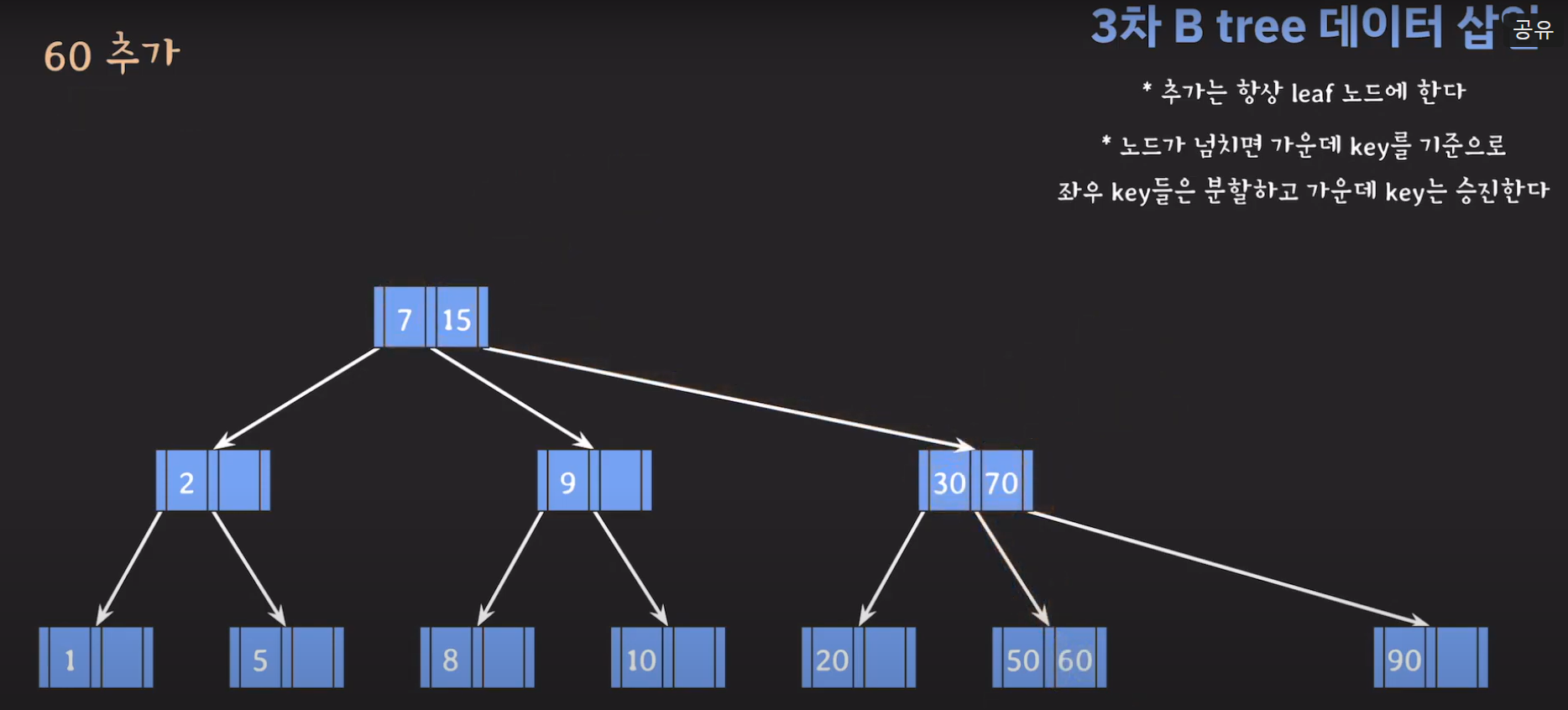
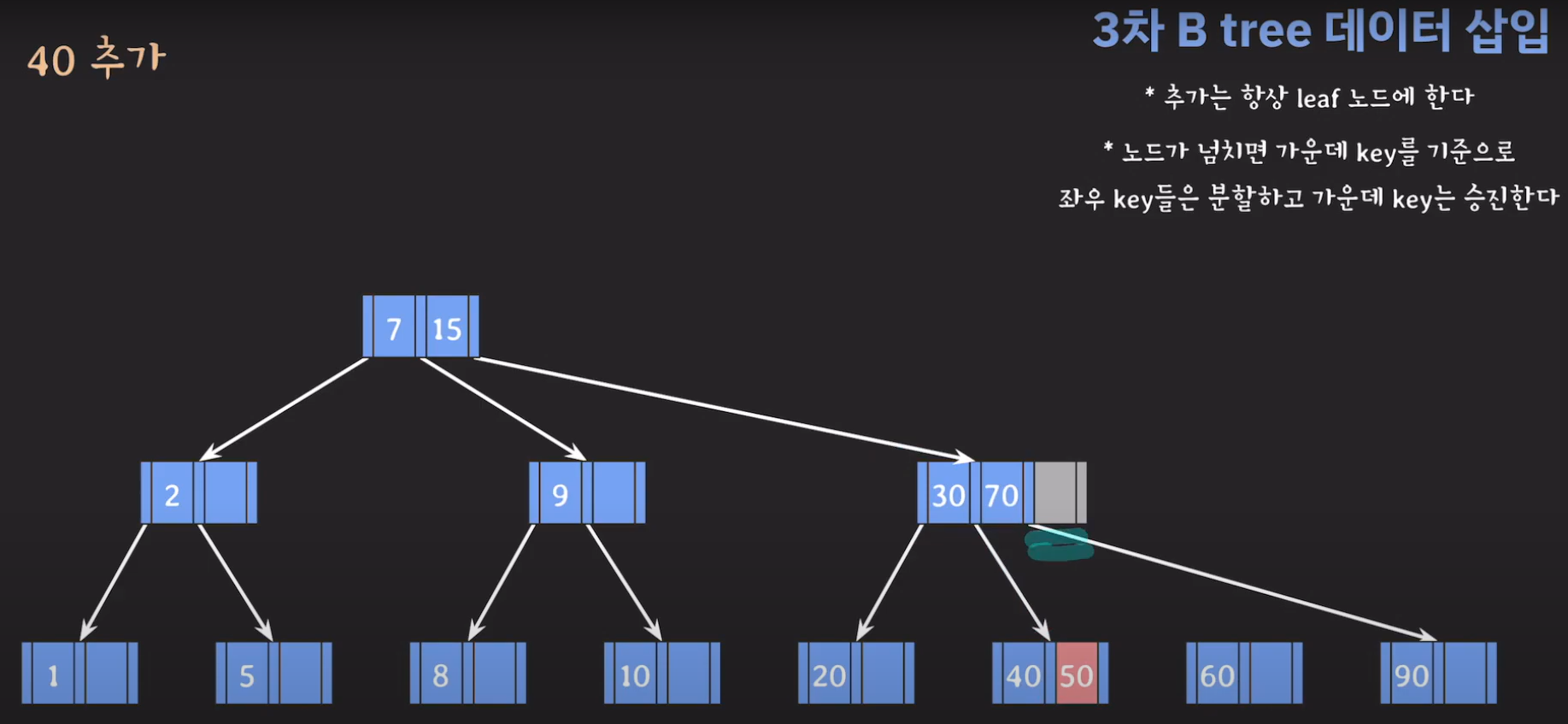
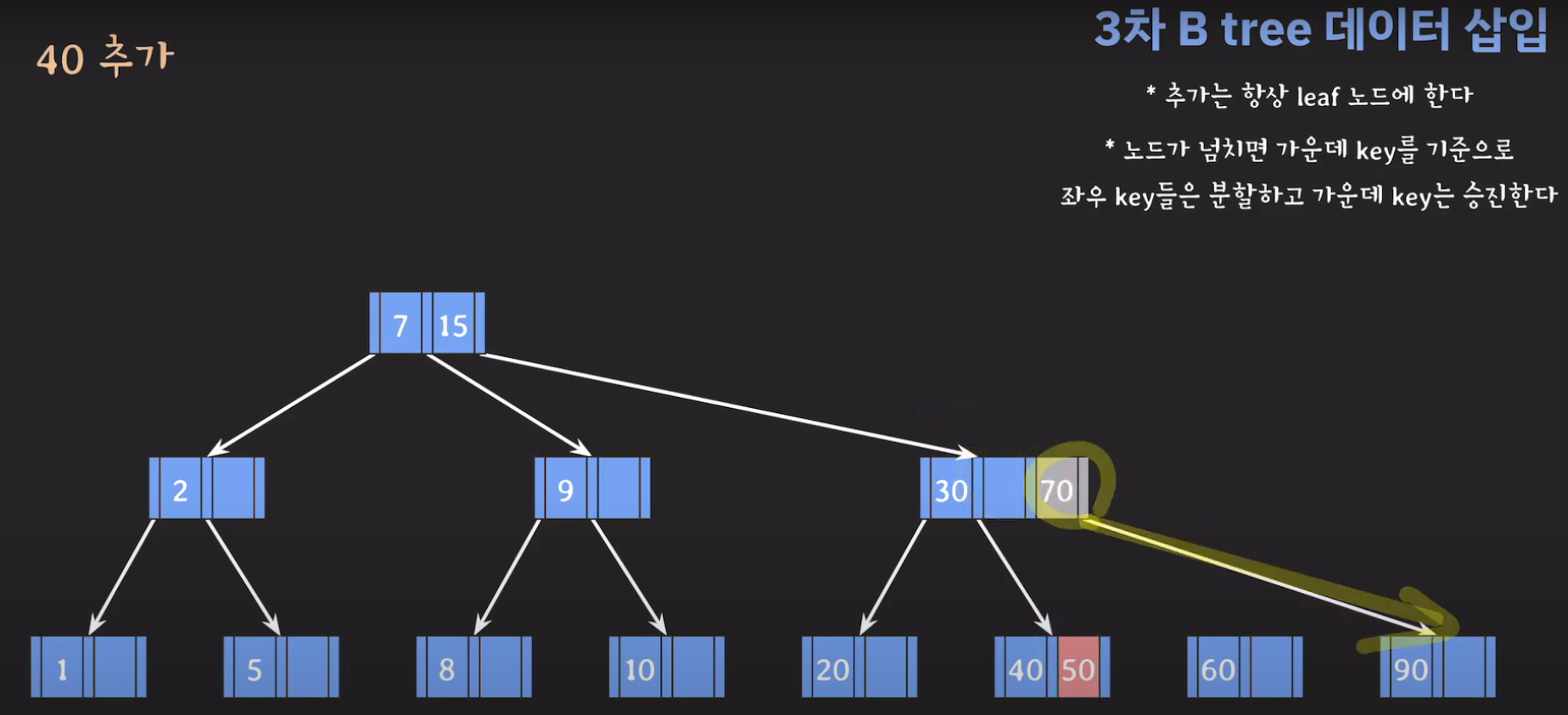
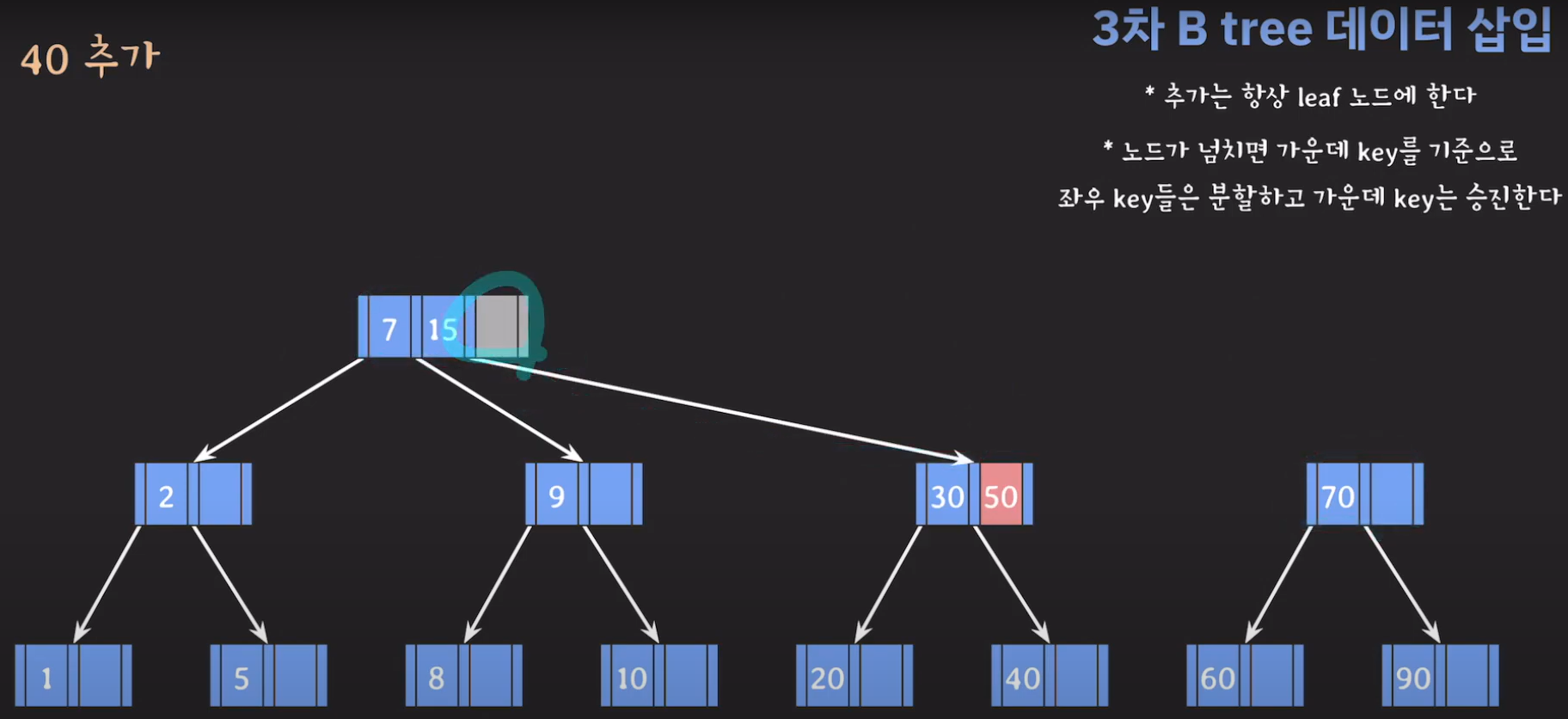
- 오름차순 정렬을 해야하기 때문에 먼저 70을 옮겨주고 ref를 바꿔줍시다.
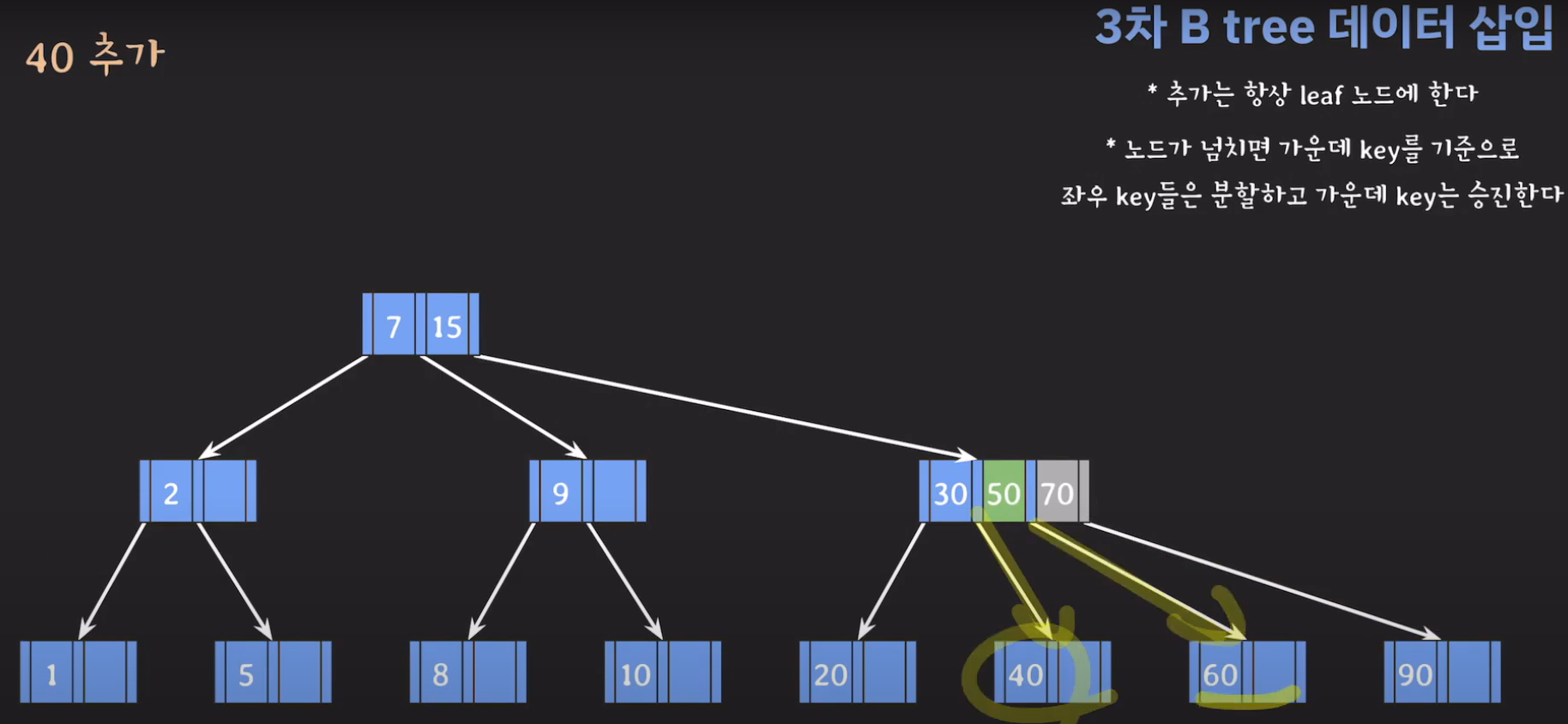
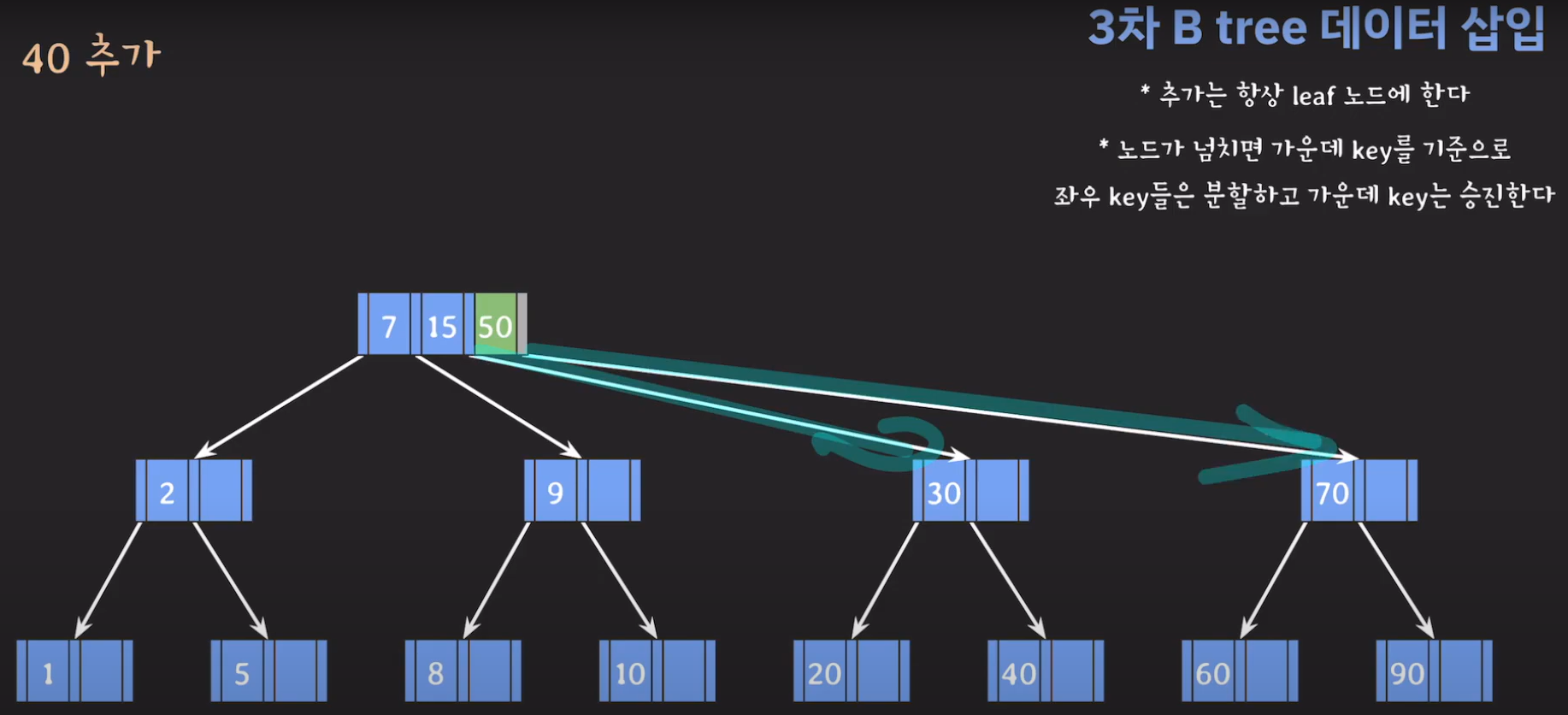
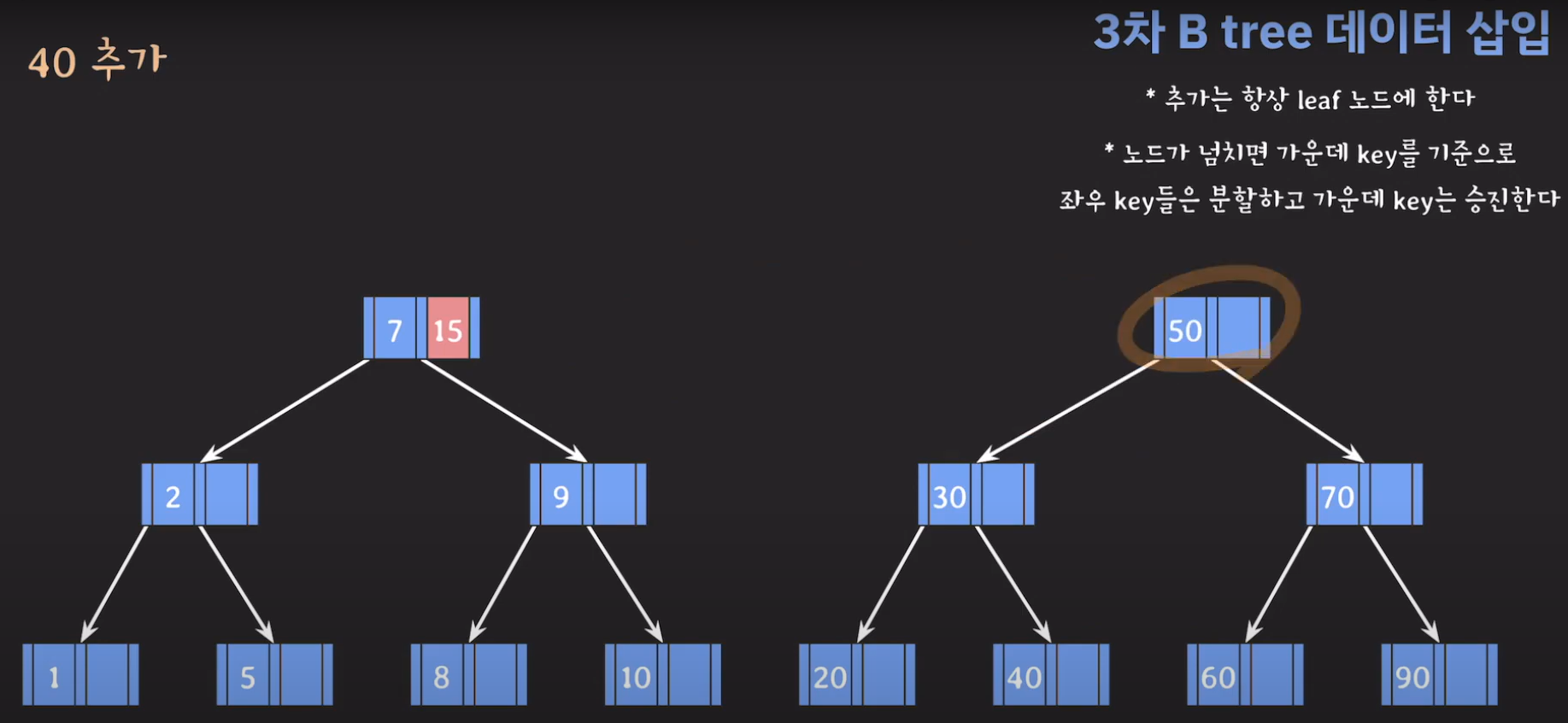
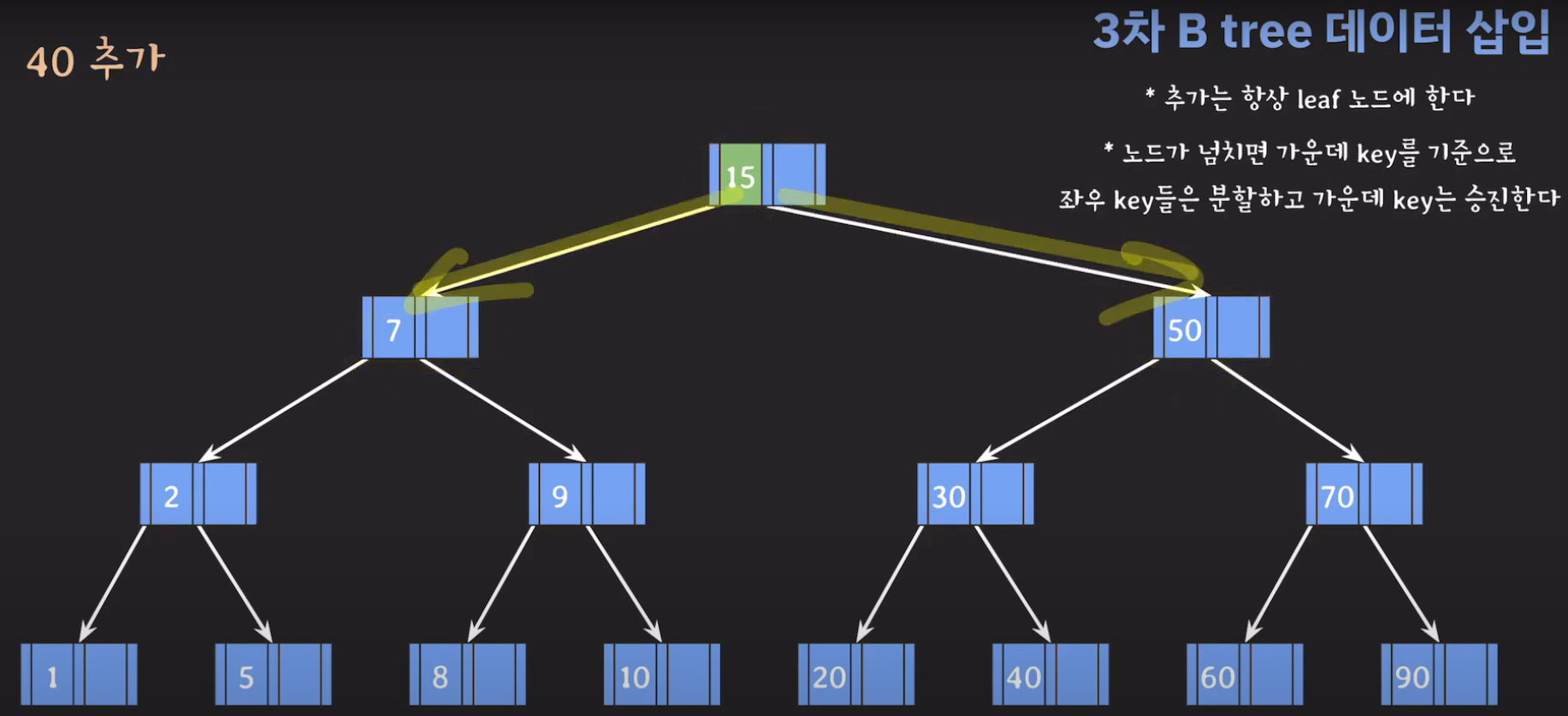
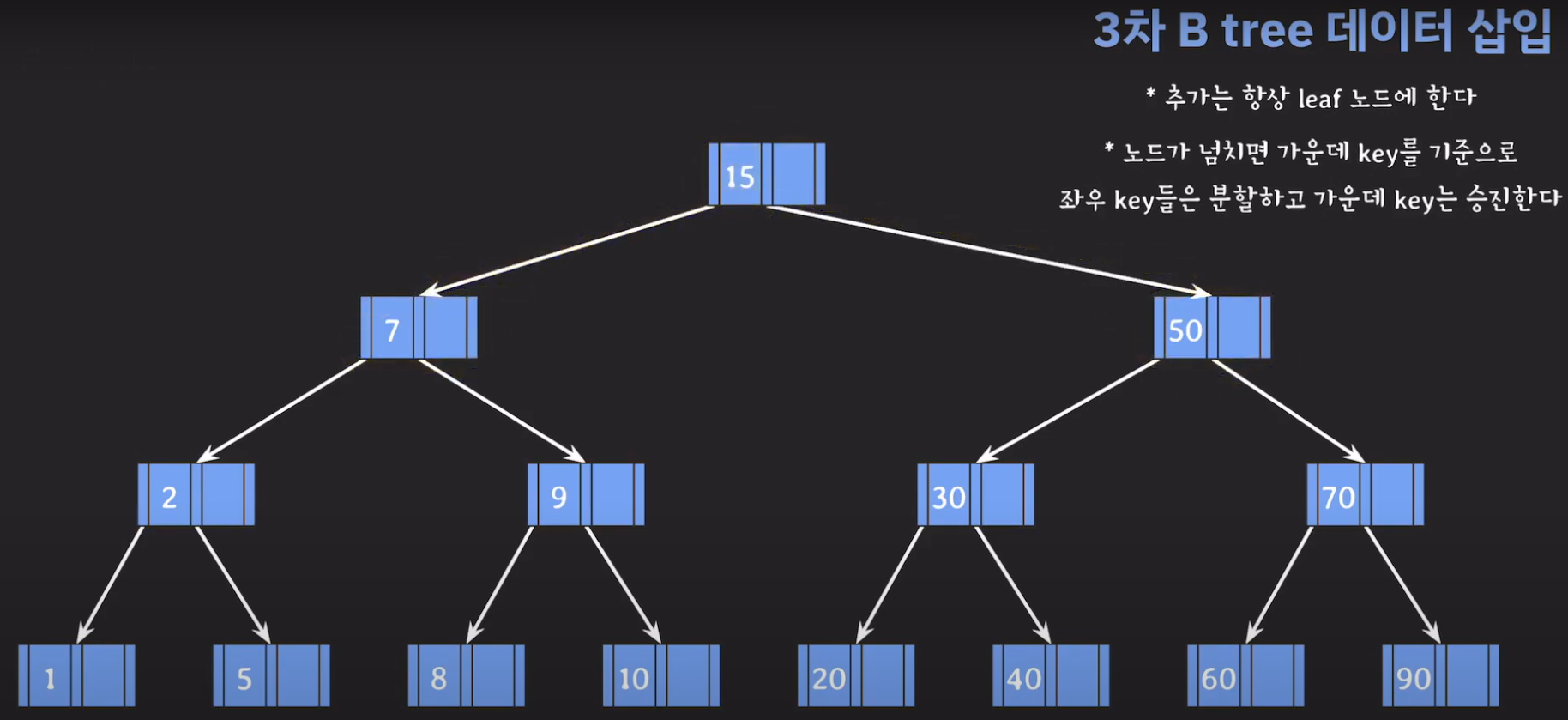
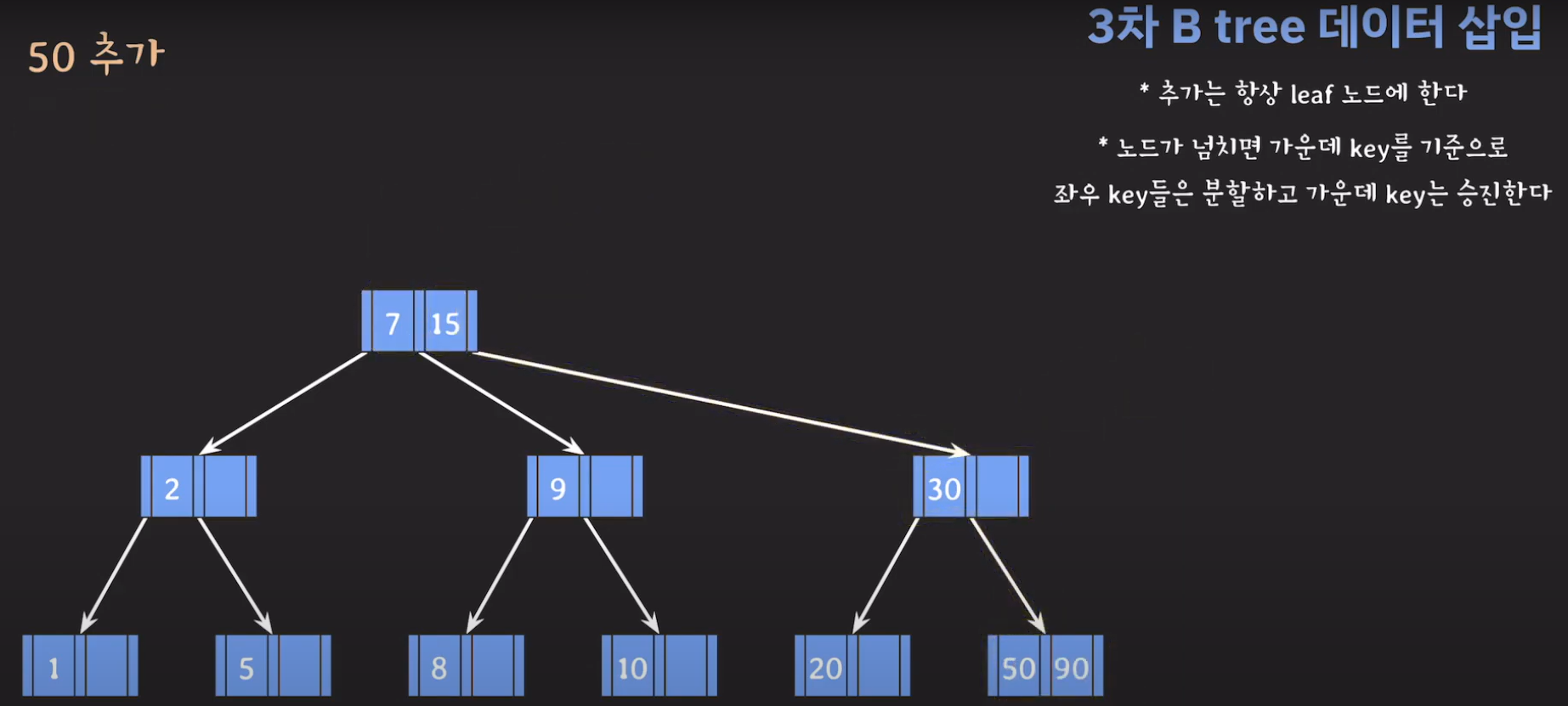
- 최종적으로는 위와 같은 Tree가 완성됩니다.
완성된 Tree를 보면 모든 leaf 노드들이 같은 레벨에 있으며 Balanced Tree인 것을 알 수 있습니다. 따라서 조회를 할 때 O(logN)을 보입니다.
cf) BST의 경우 한쪽으로 노드가 몰리면 O(N)의 성능을 보입니다.
정리하면 B Tree는 다음과 같은 성질을 갖습니다.
B Tree 데이터 삭제
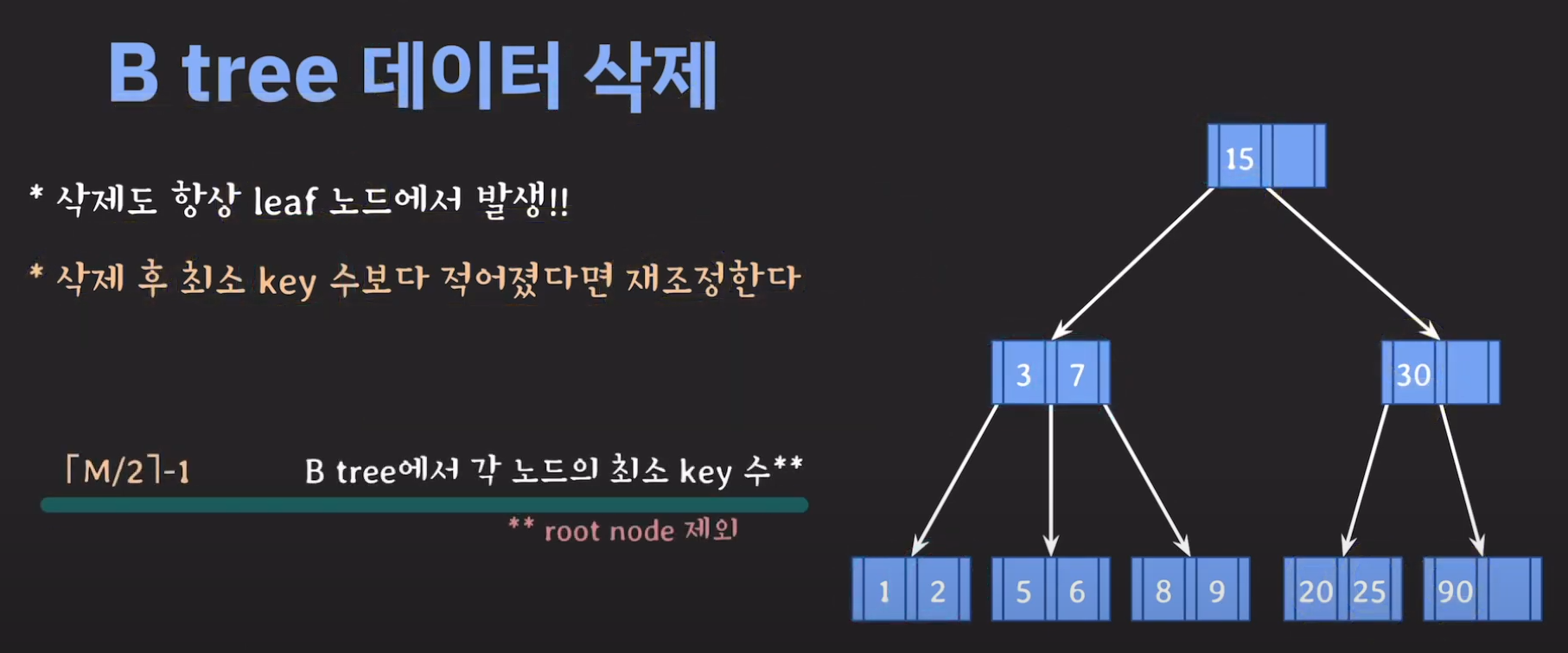
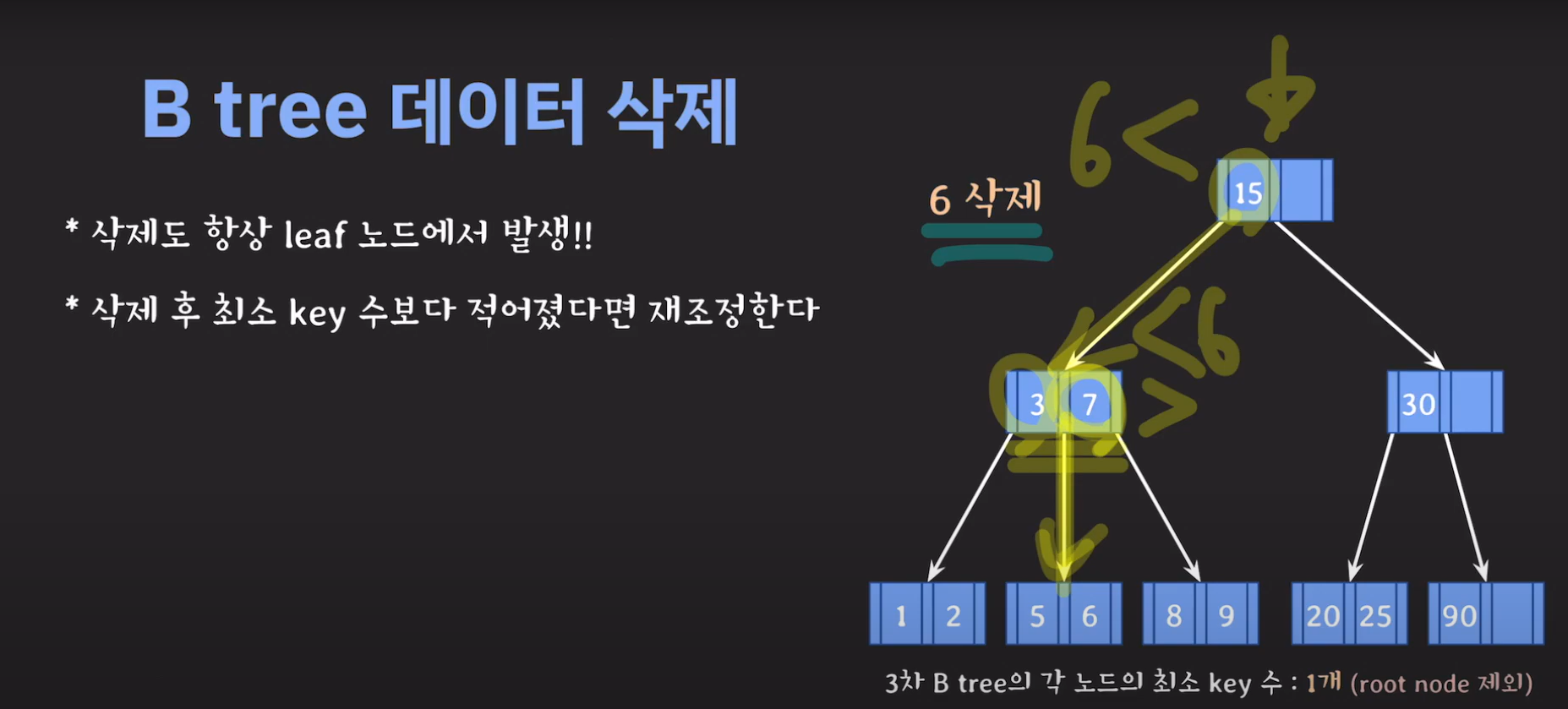
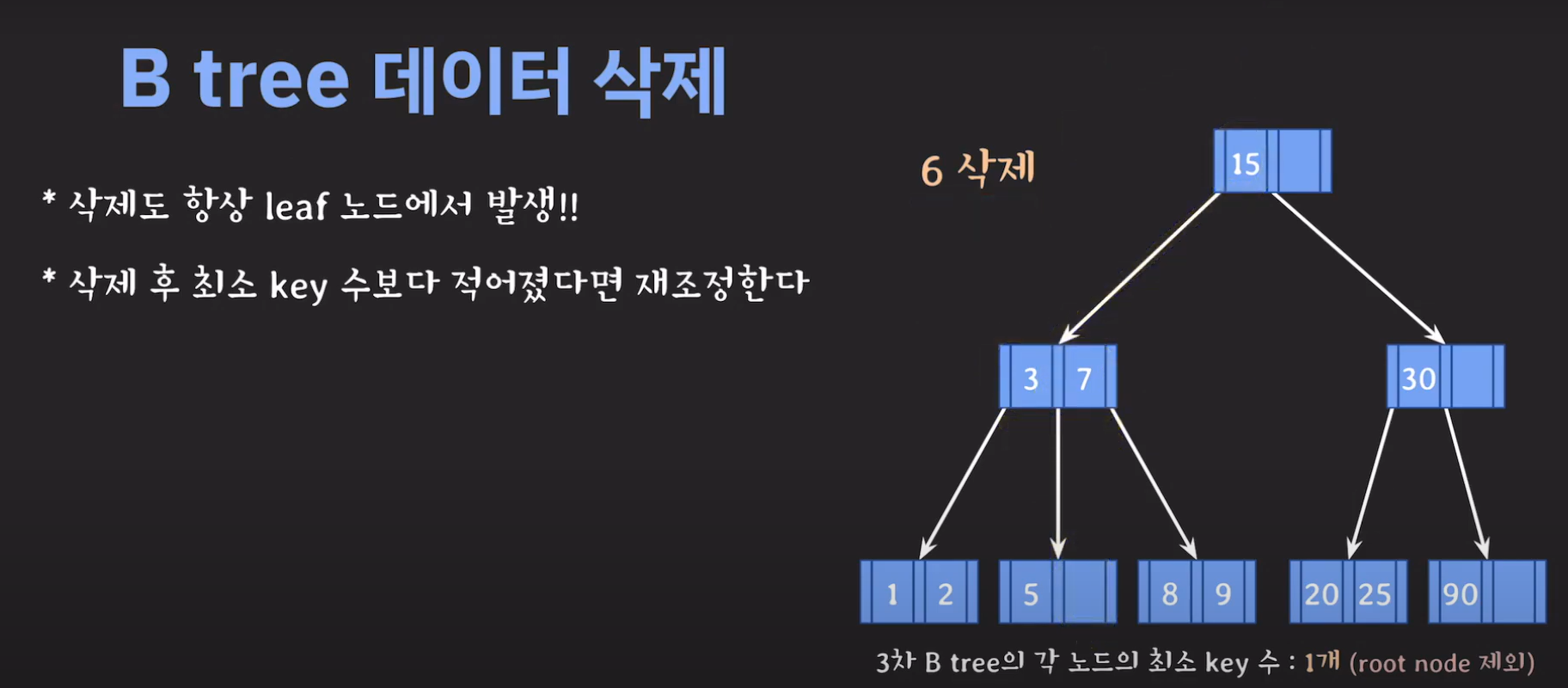
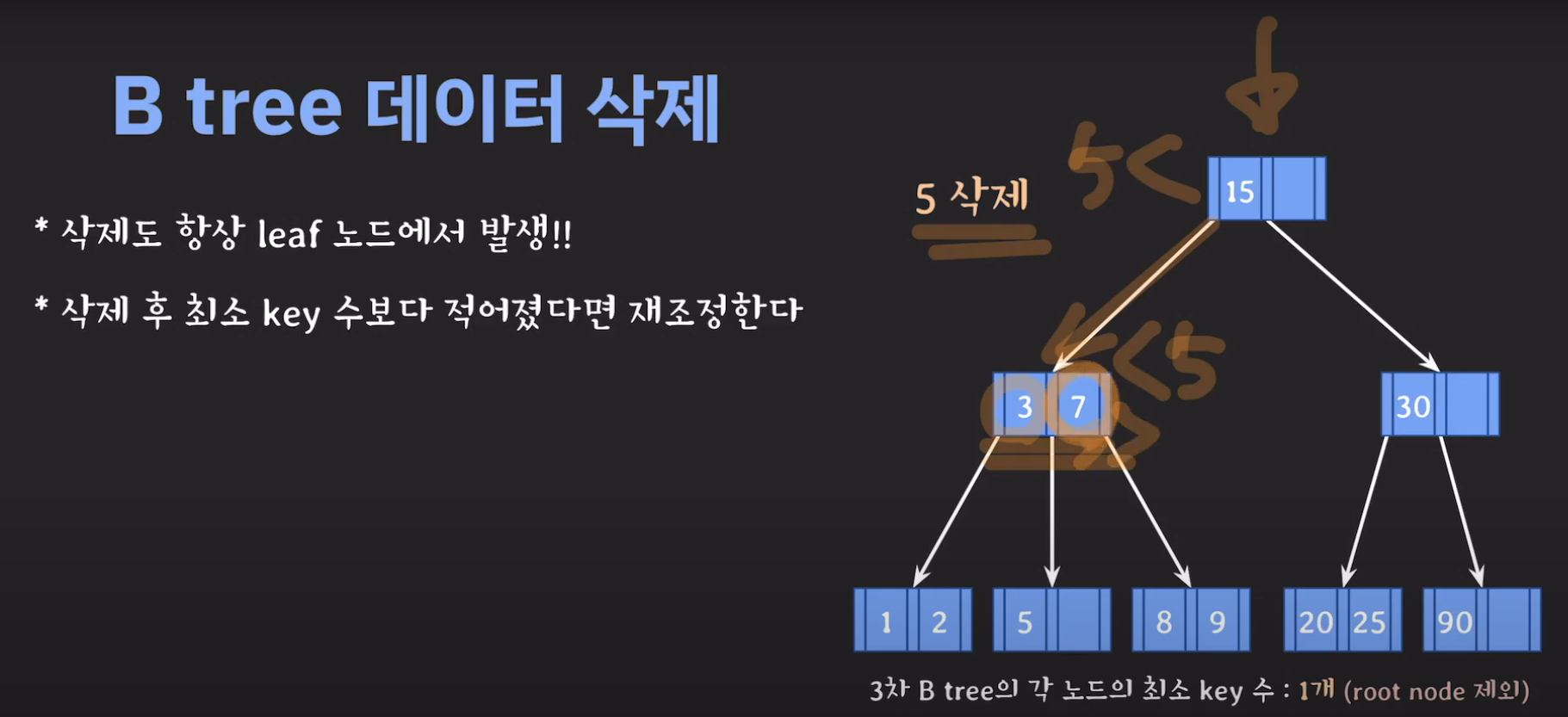
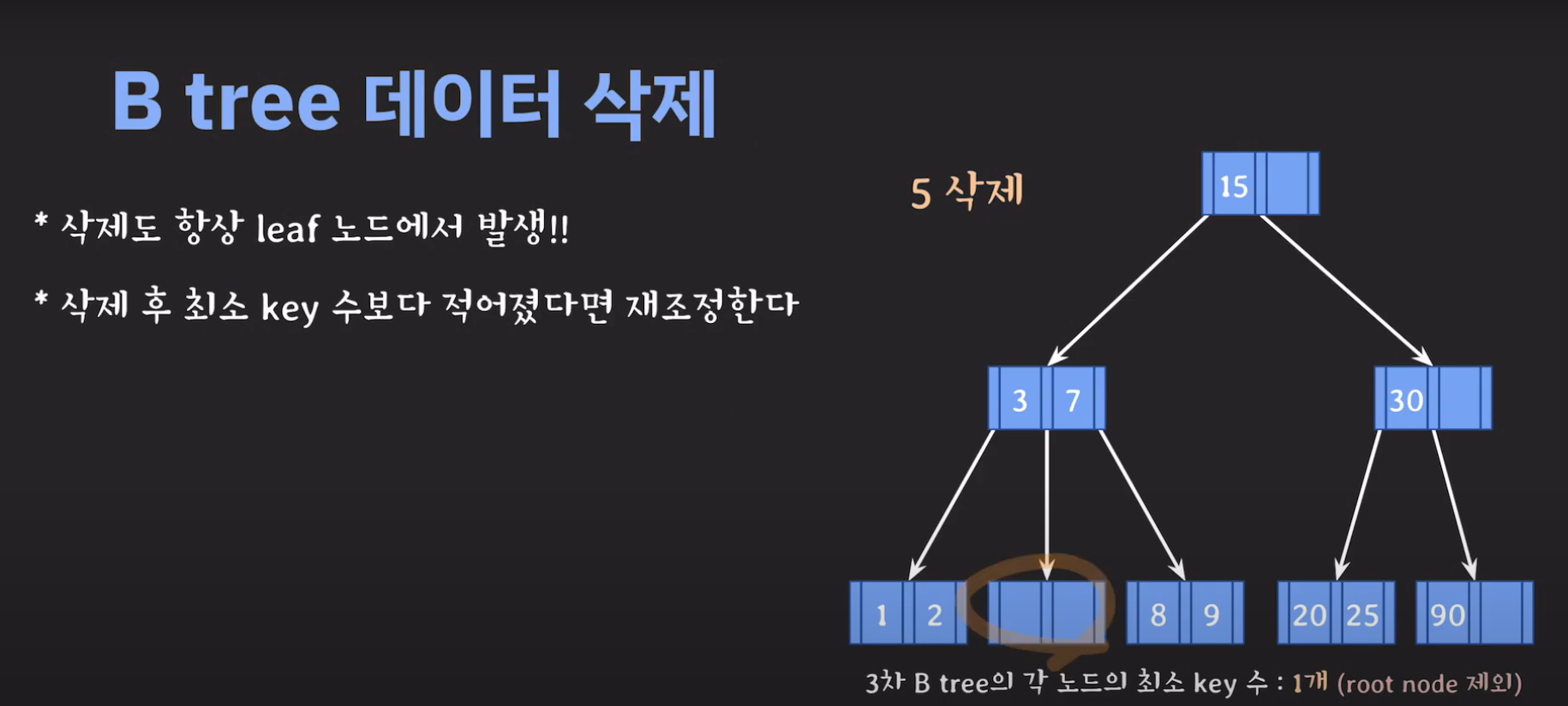
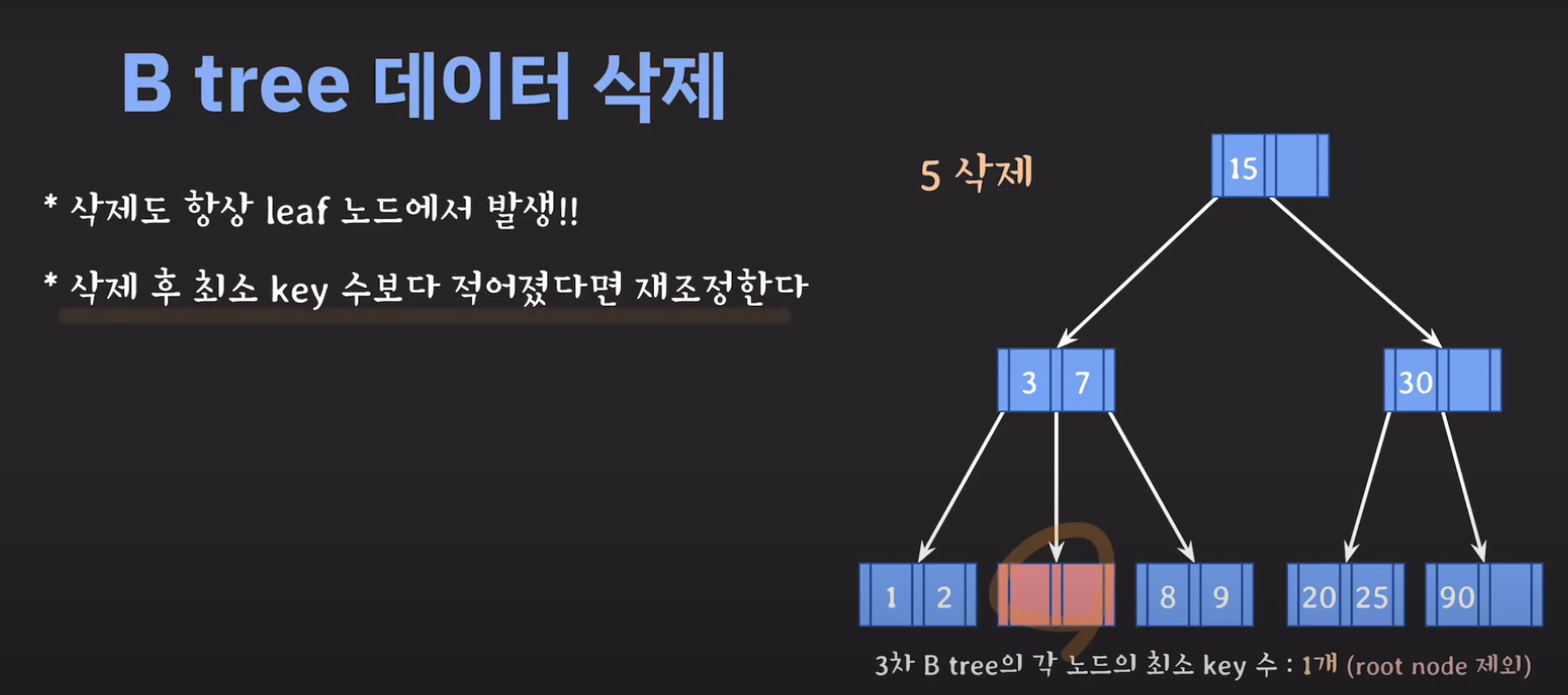
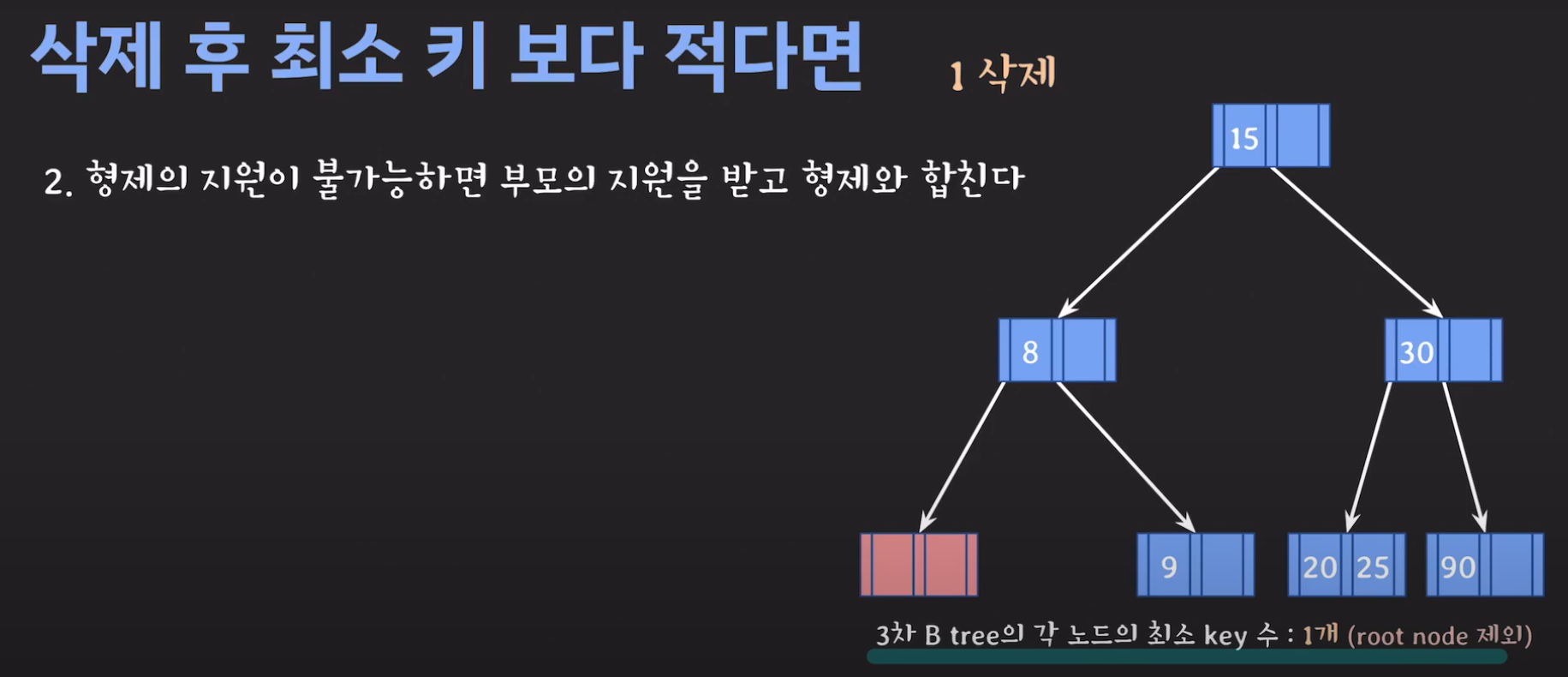
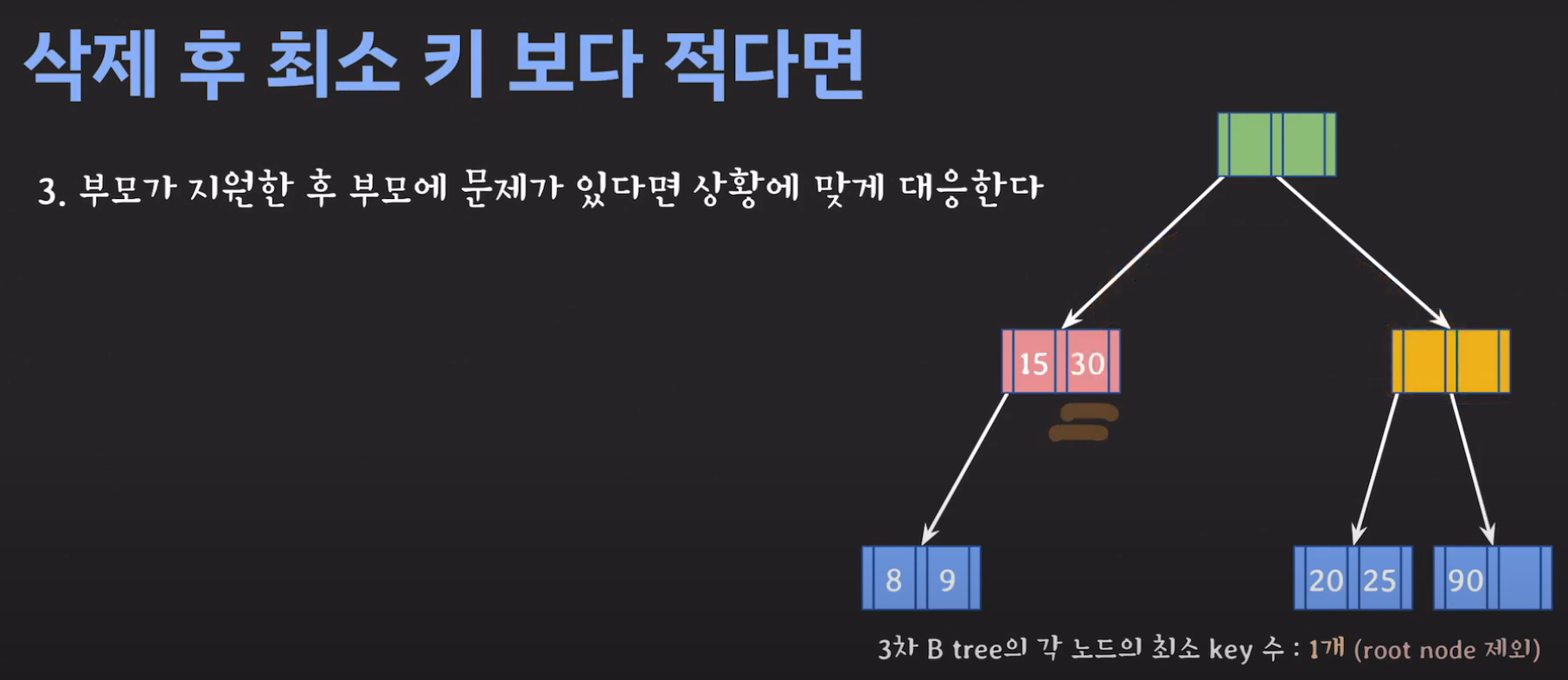
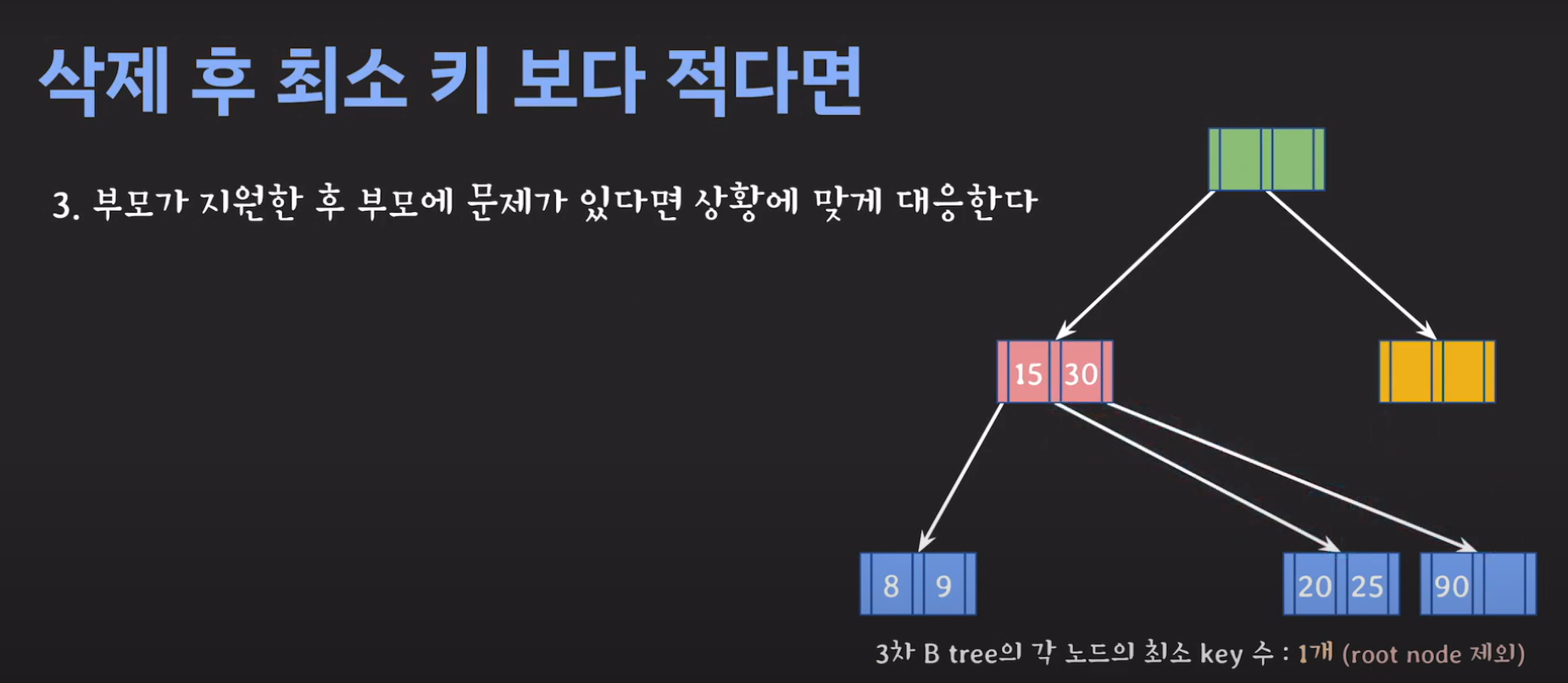
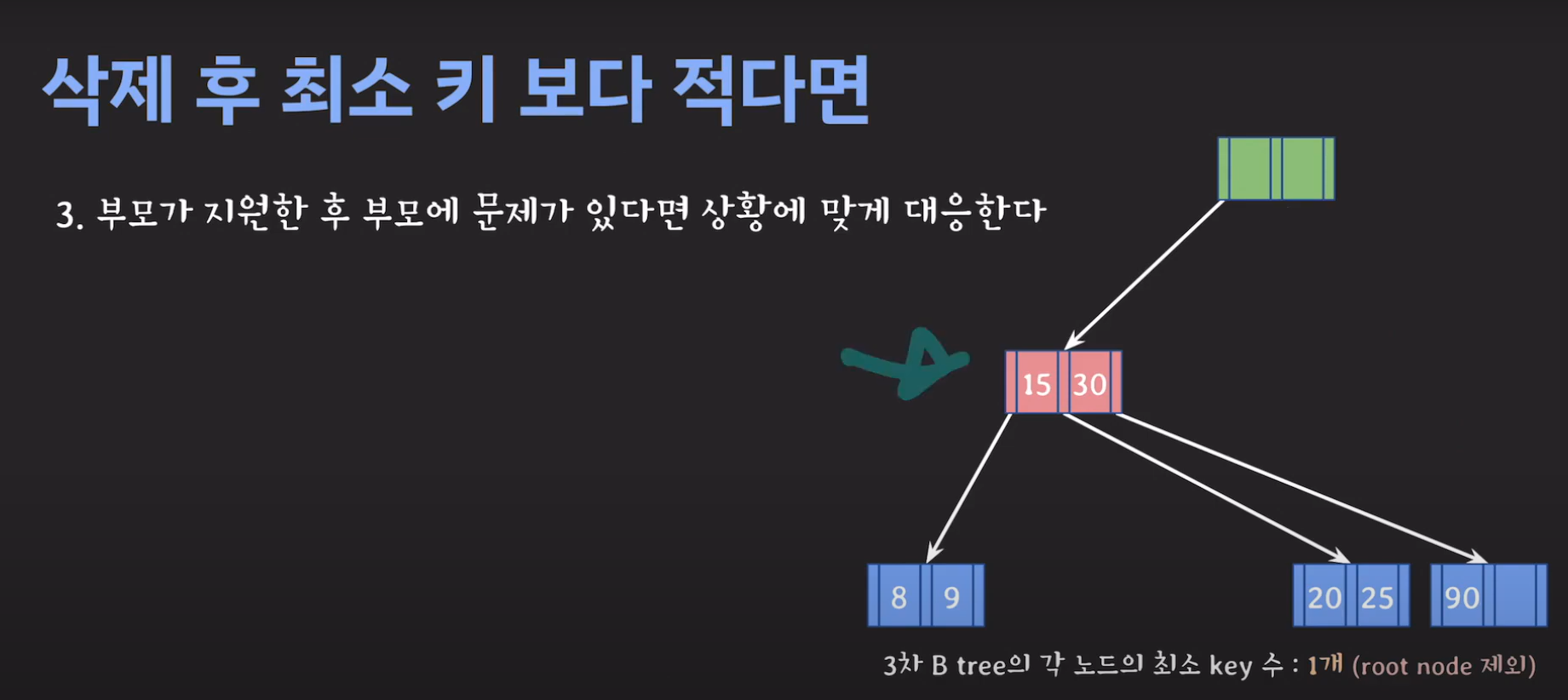
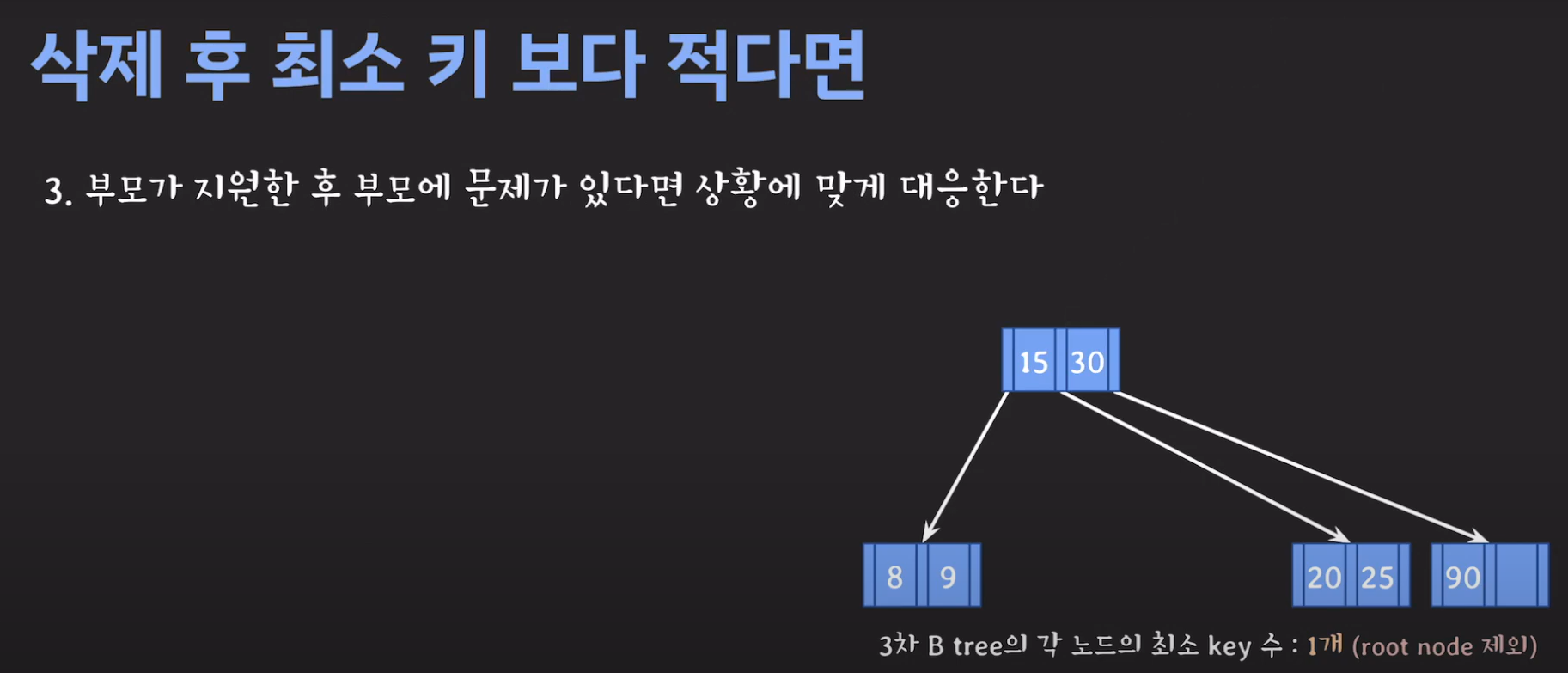
- 3차 B Tree의 조건을 위반하였으므로 해당 노드를 처리해주어야 합니다.
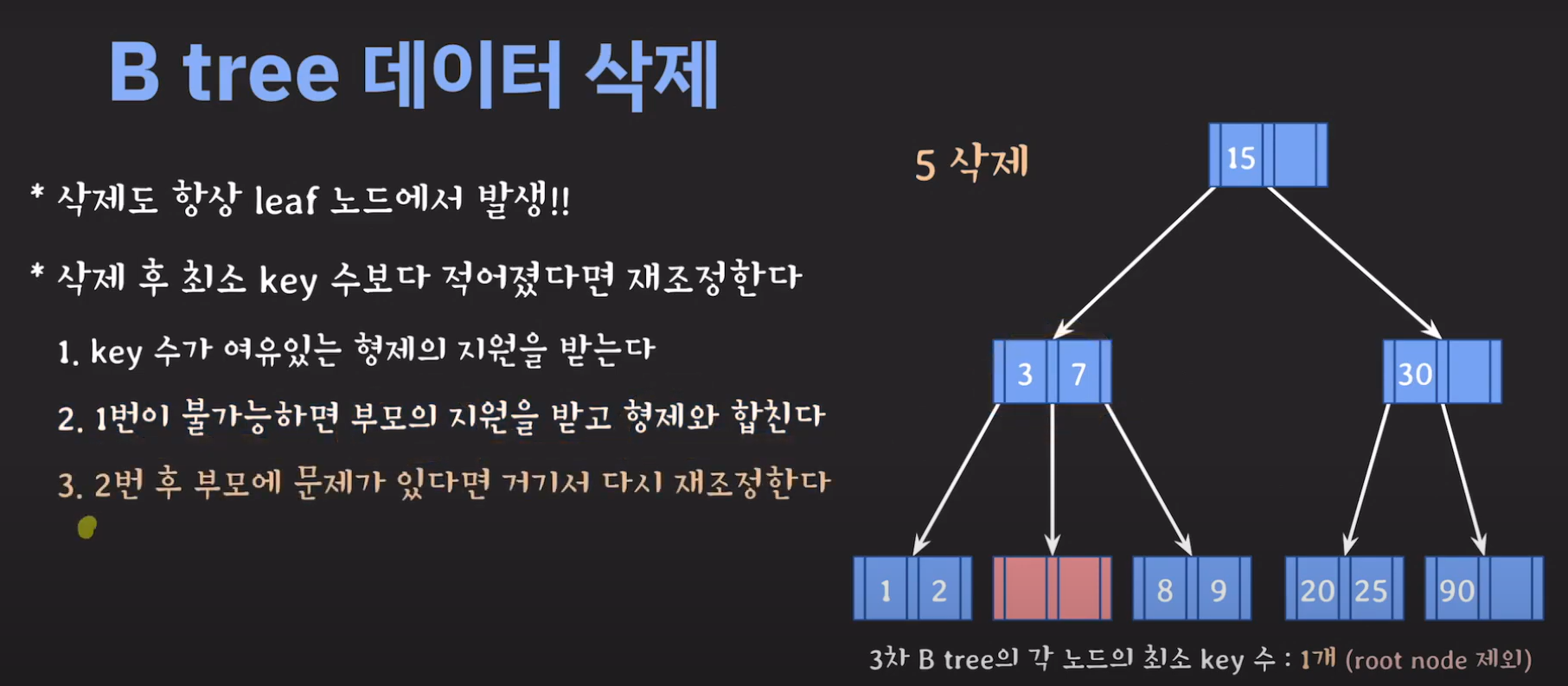
위와 같은 과정을 거쳐 해결하게 됩니다. 예시와 함께 생각해보도록 합시다.
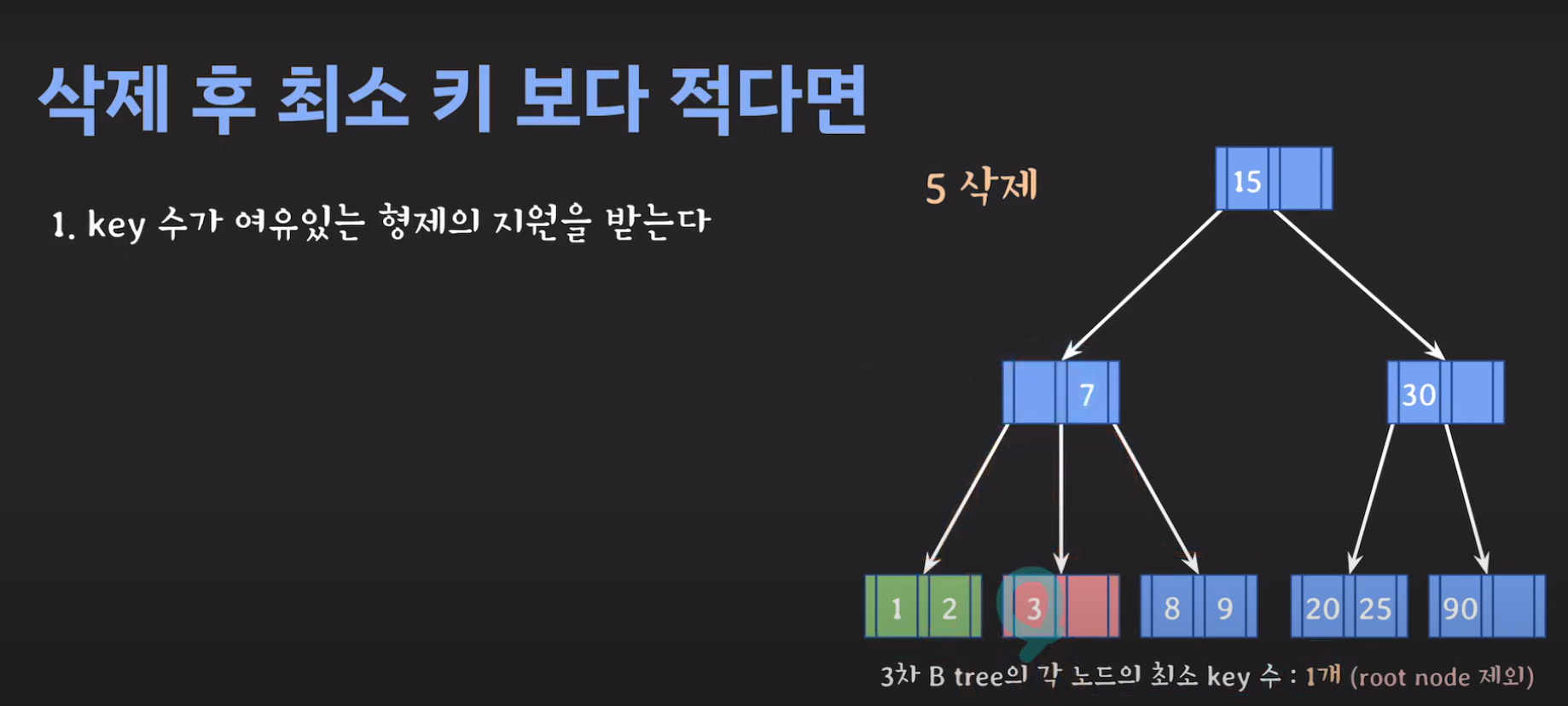
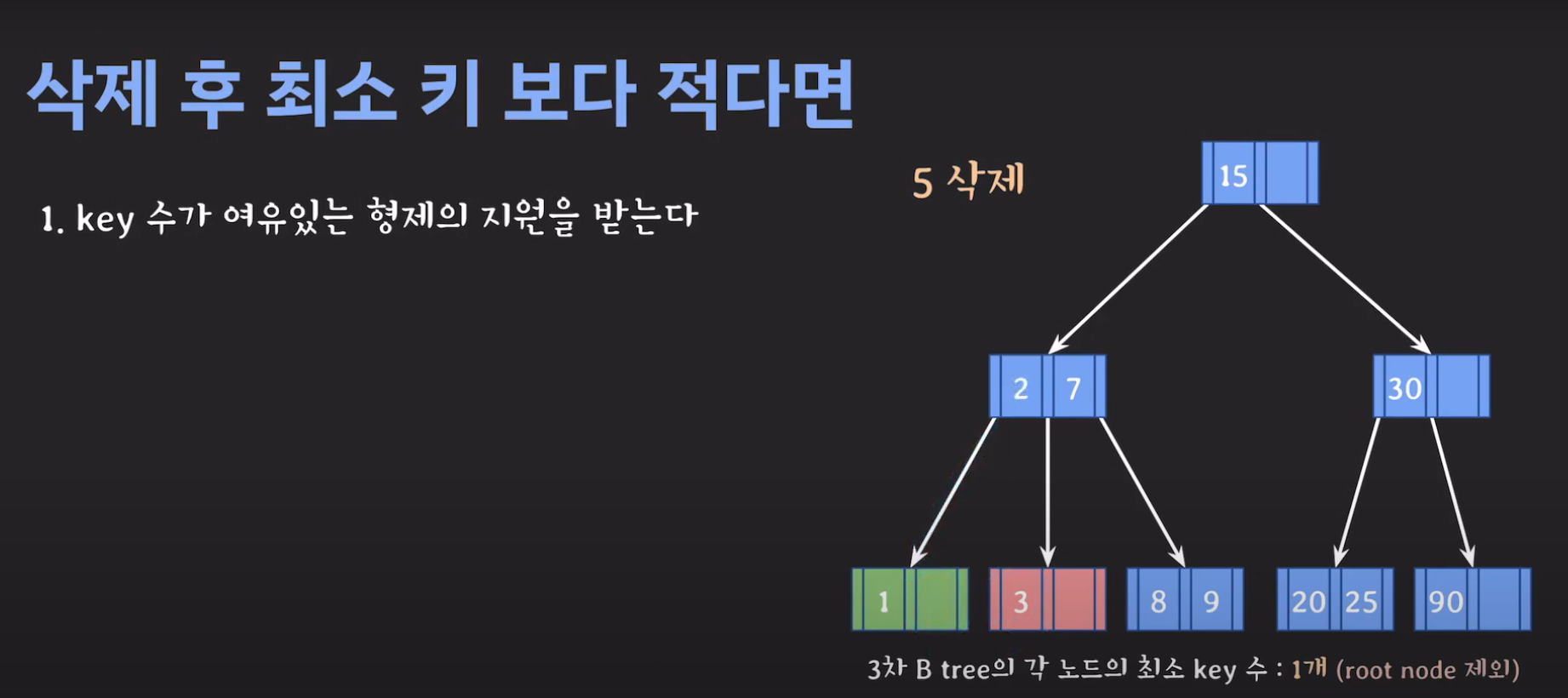
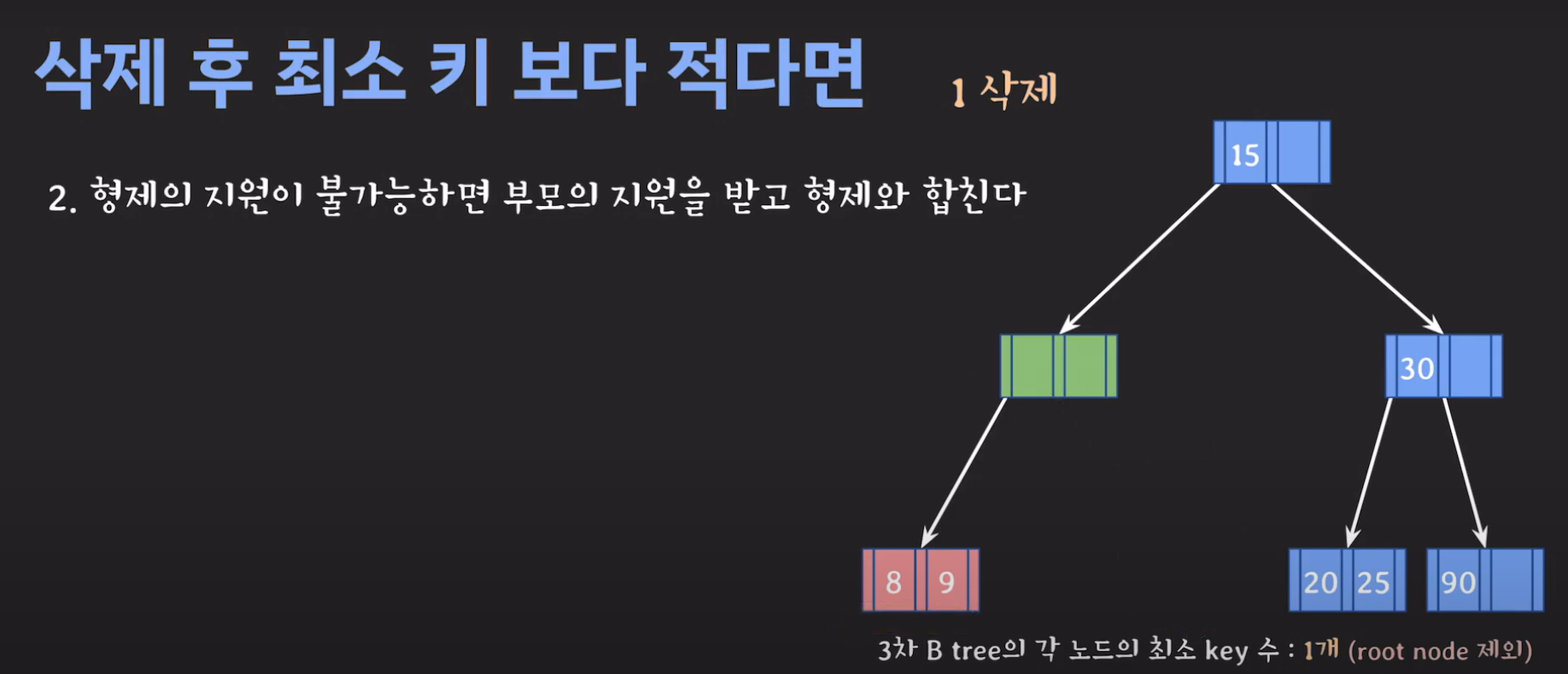
- BST의 특징을 만족해야 하므로 2를 바로 넘겨 주어서는 안됩니다.
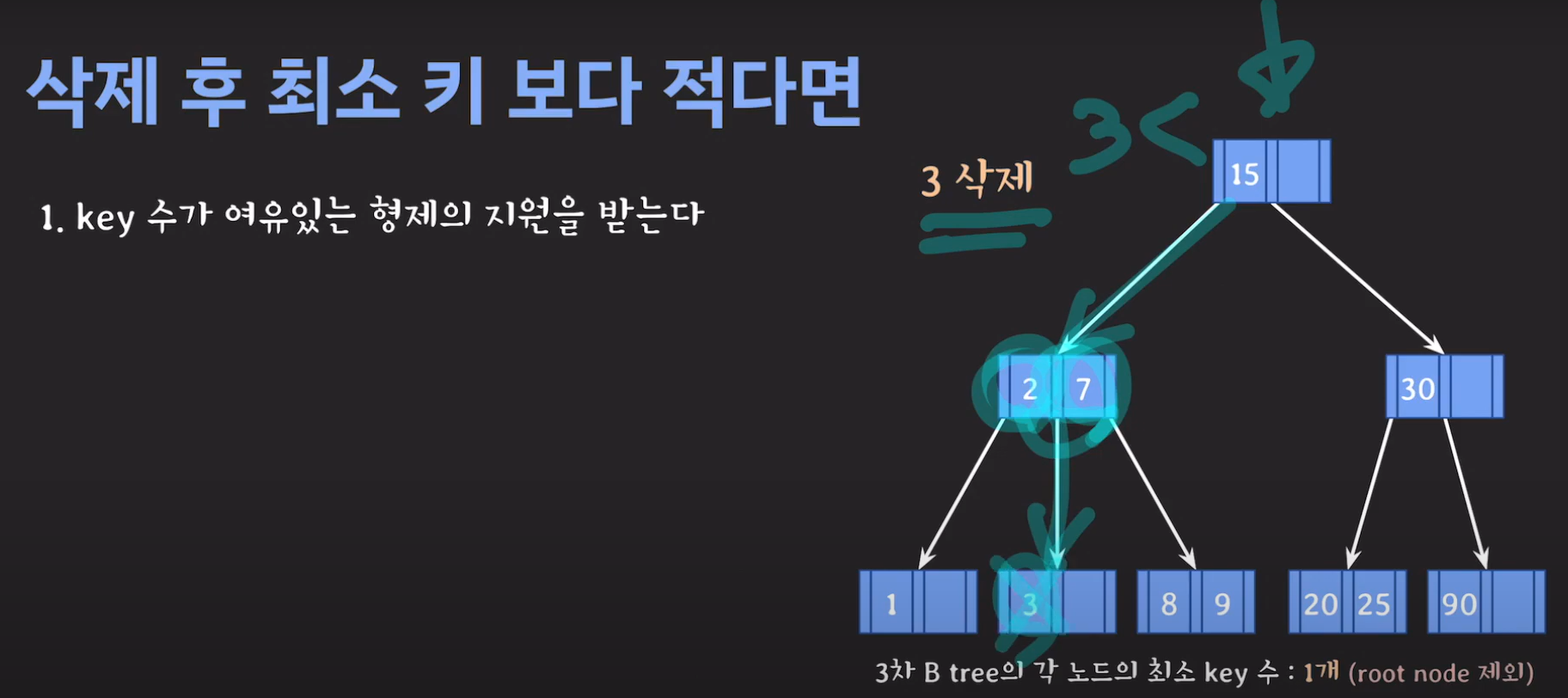
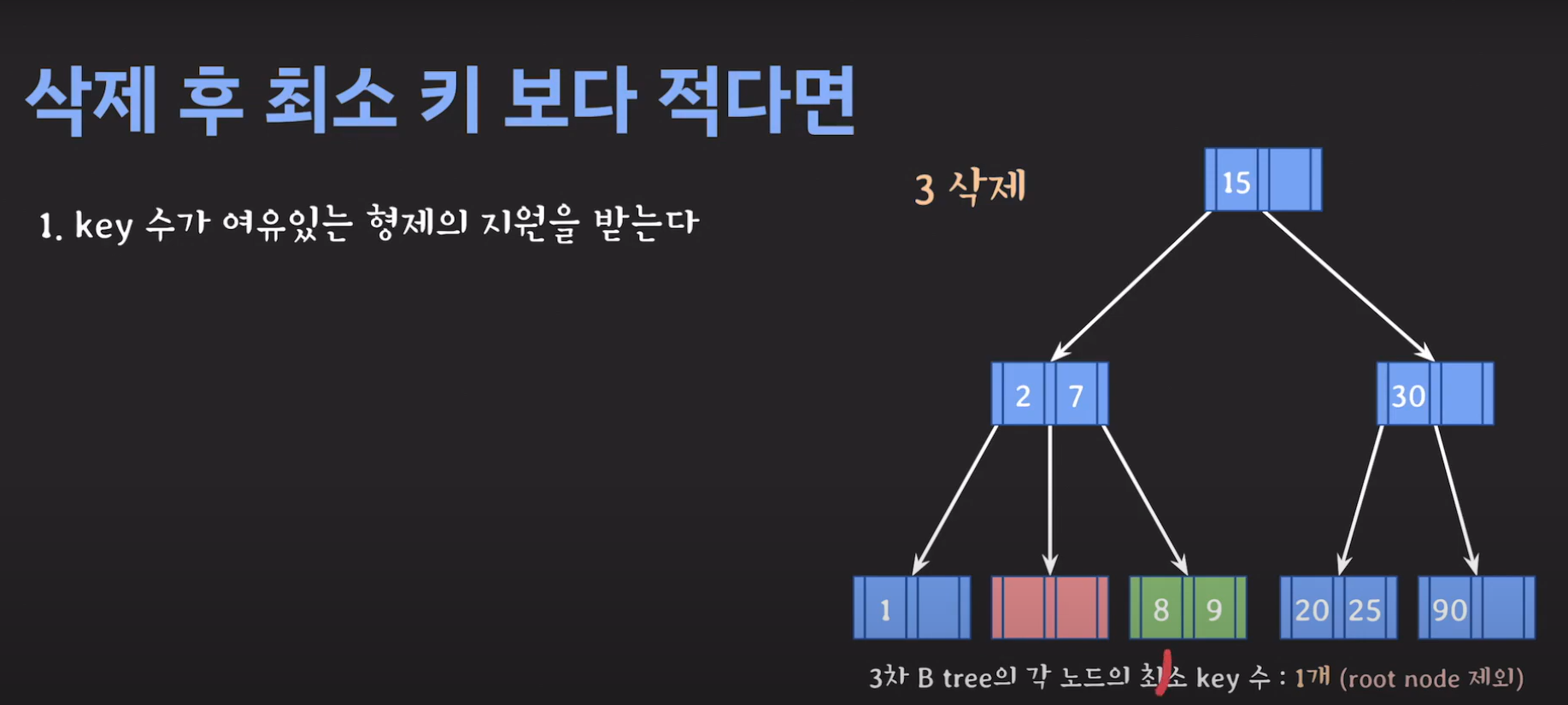
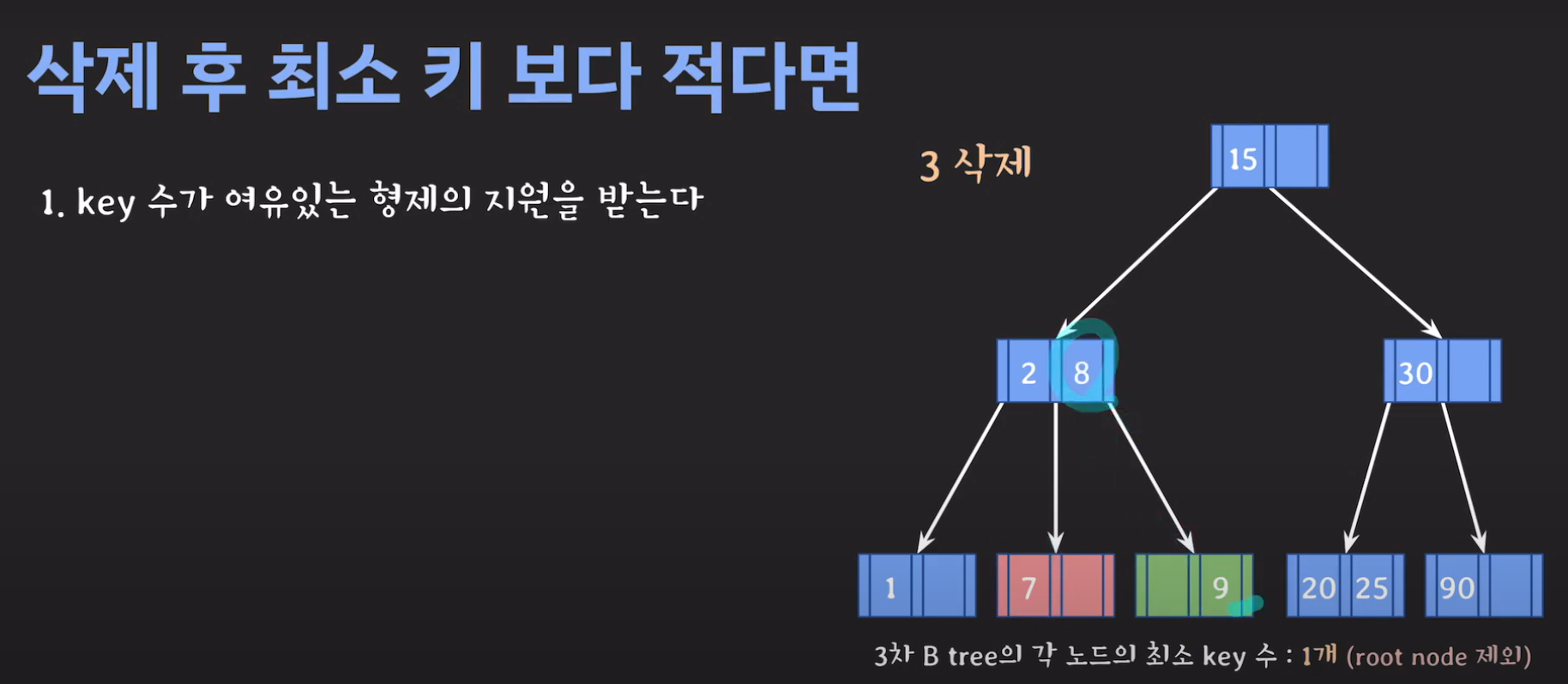
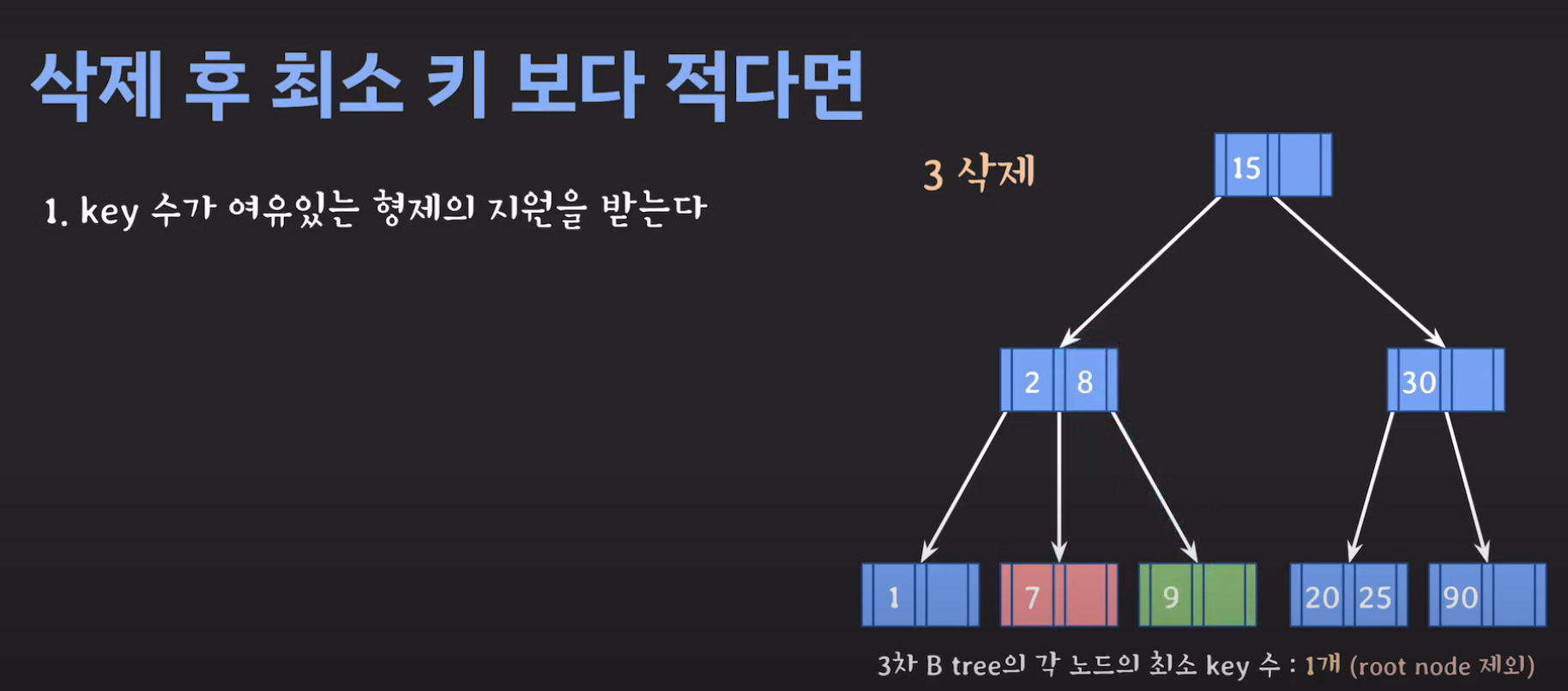
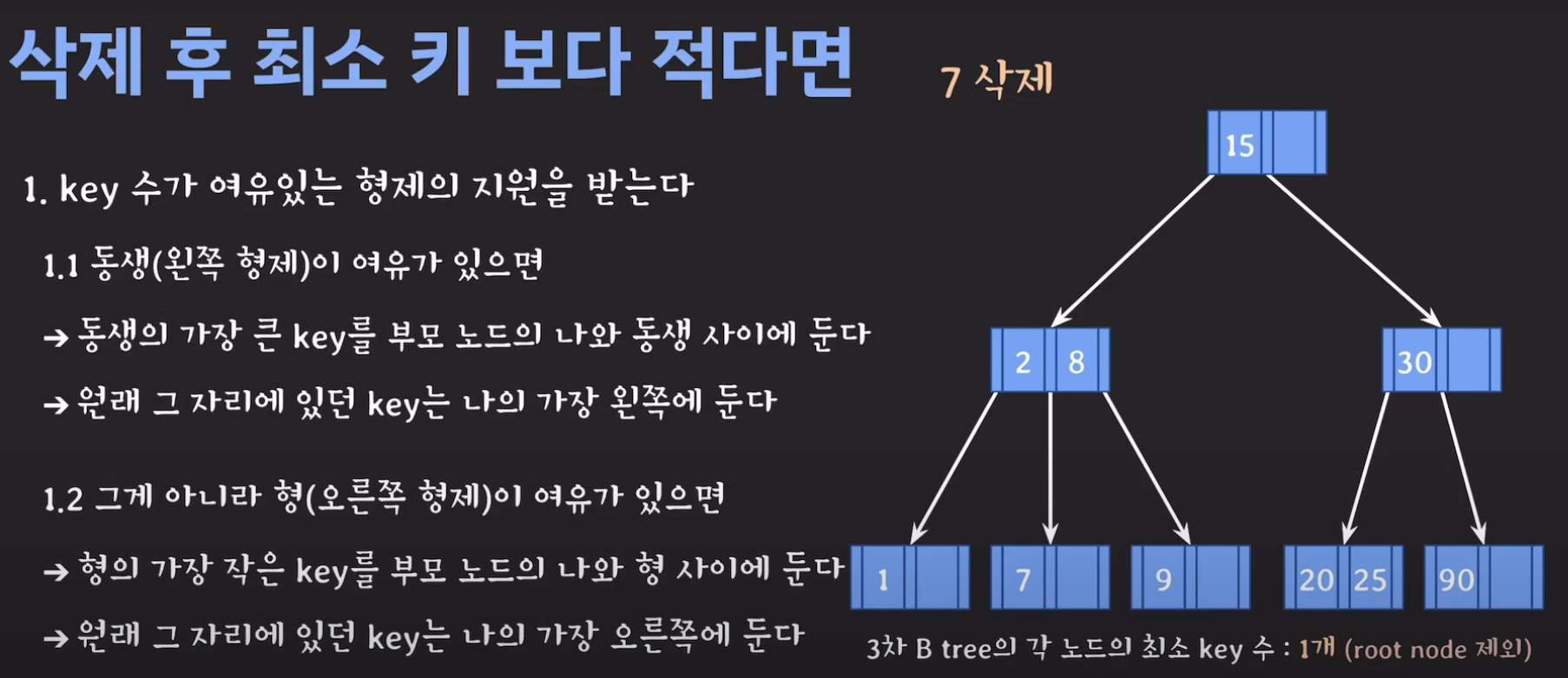
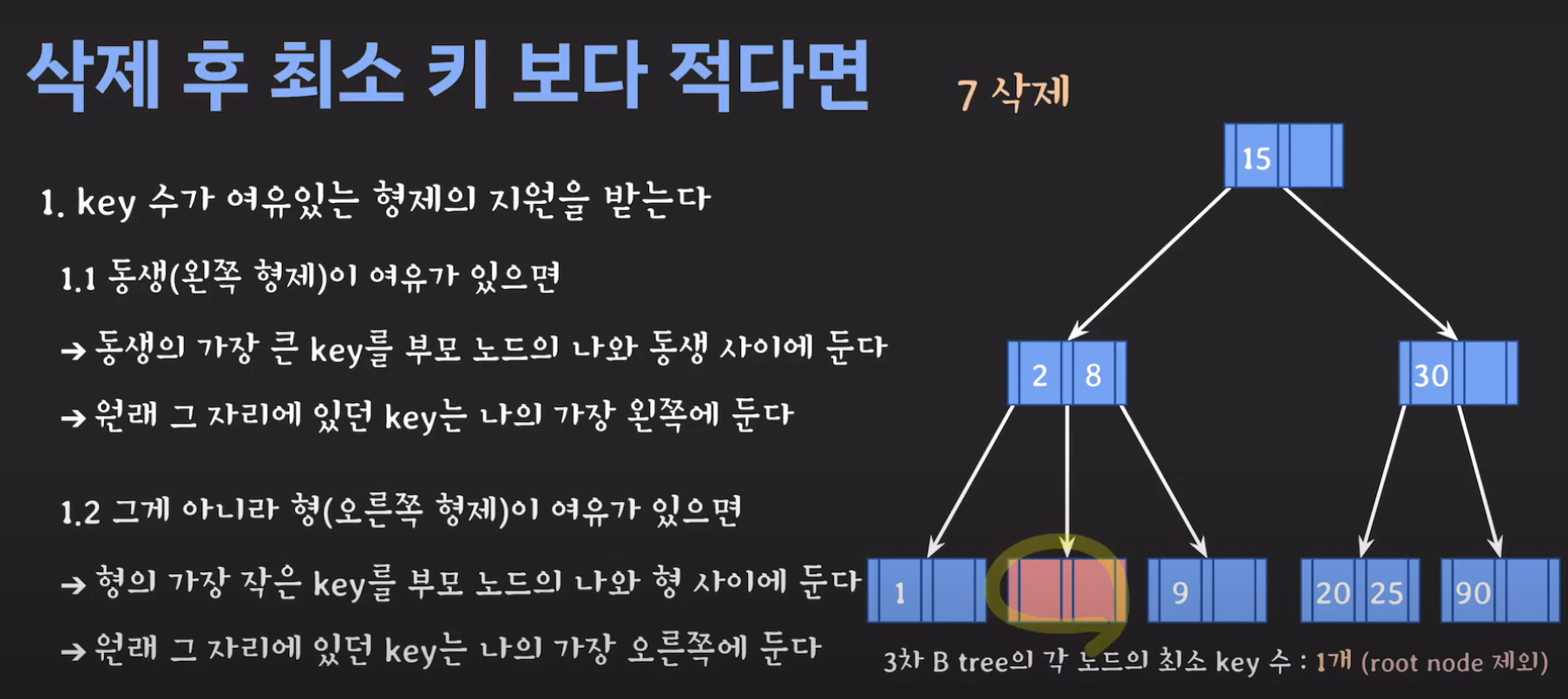
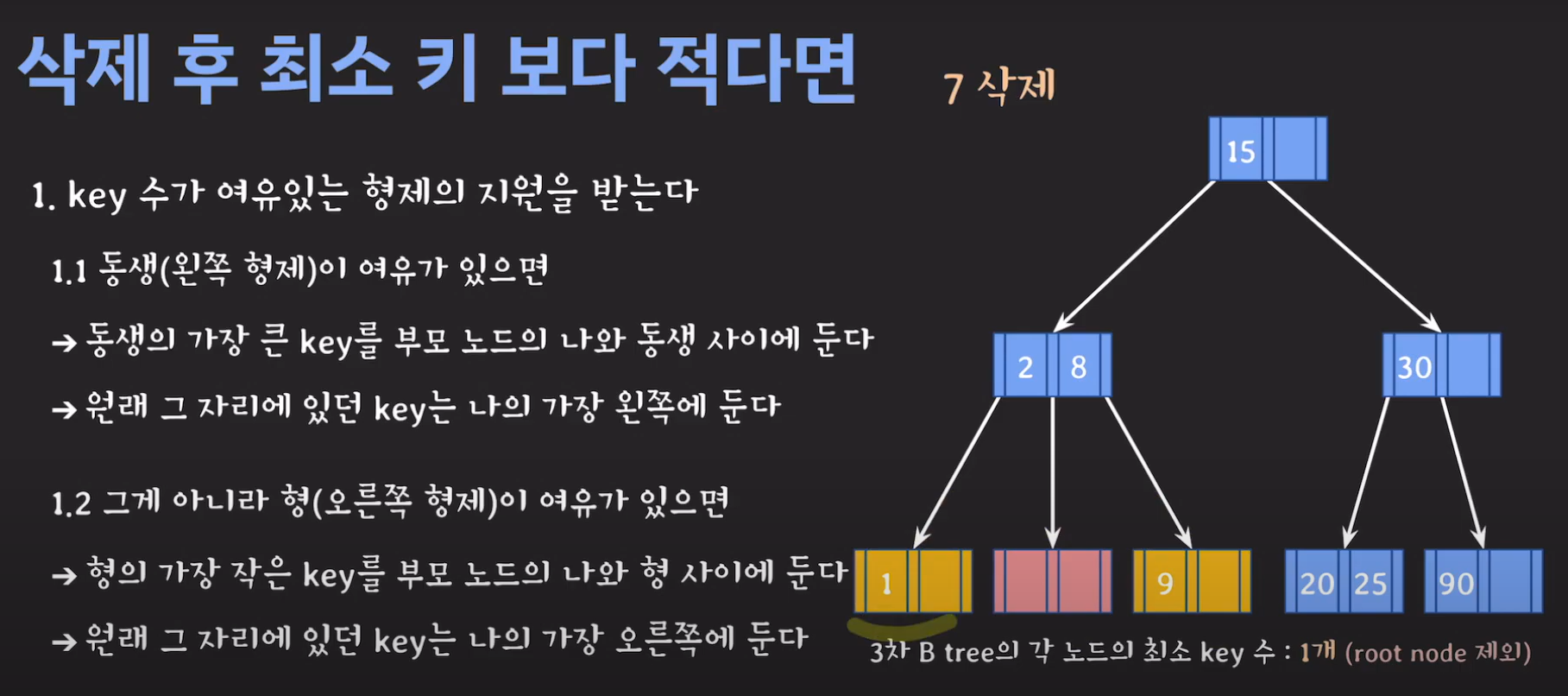
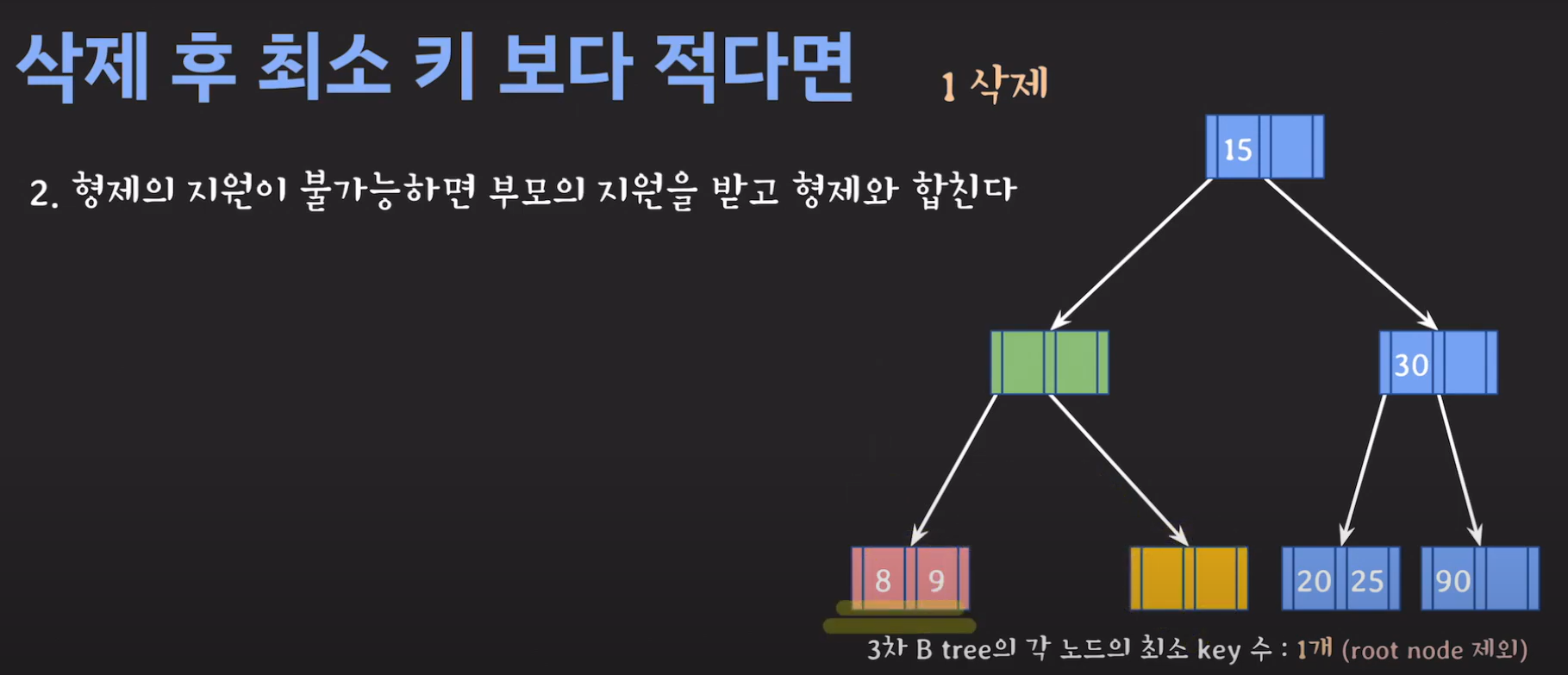
- 현재 상황은 형제한테 도움을 받을 수 없는 상황입니다. 따라서 1번의 방법으로 이를 해결 할 수 없습니다.
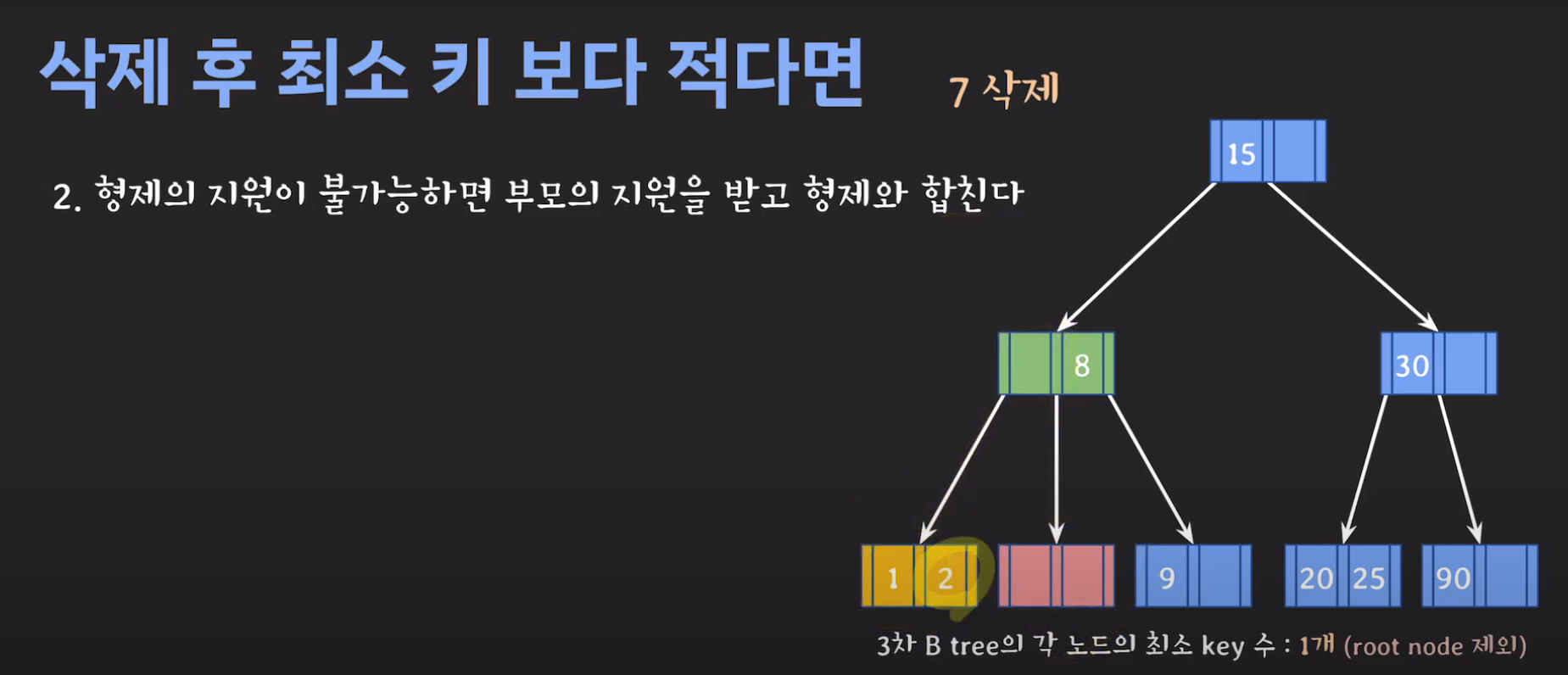
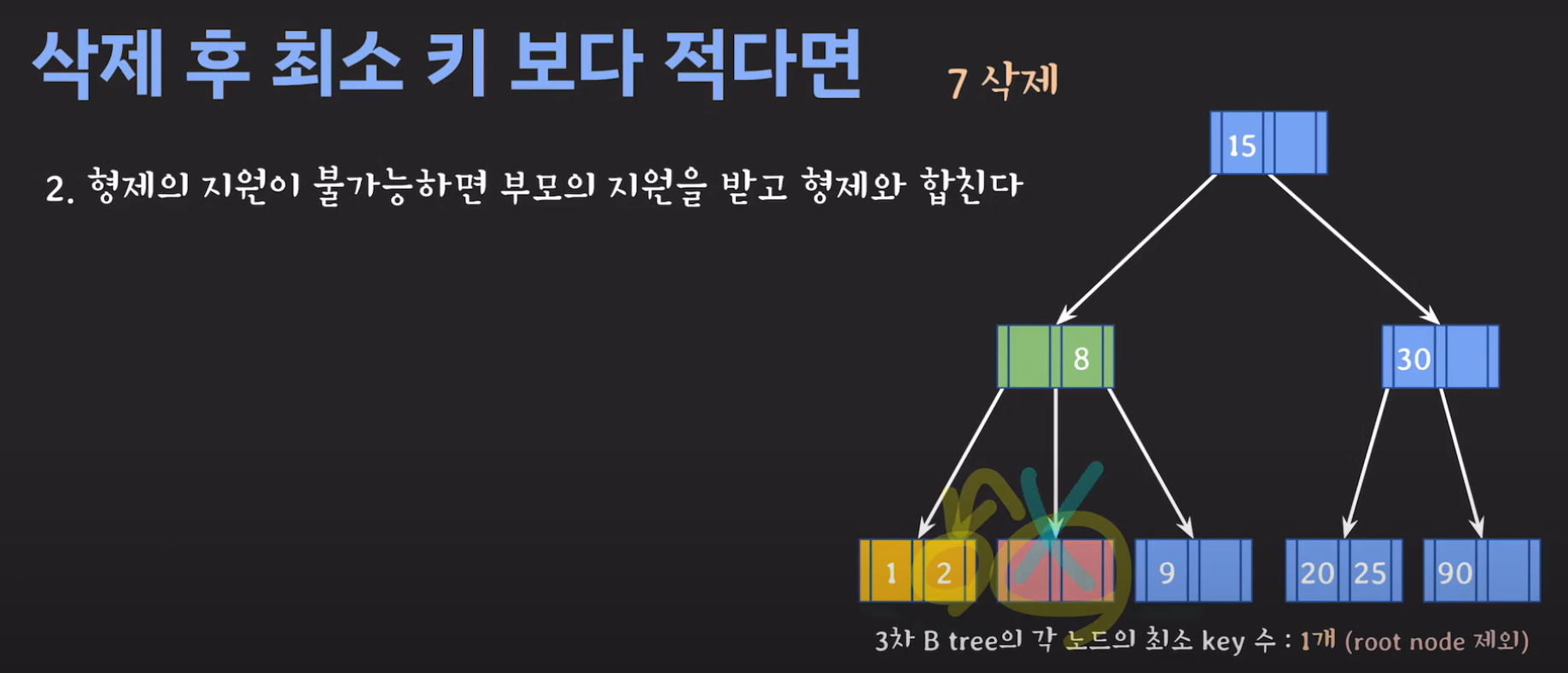
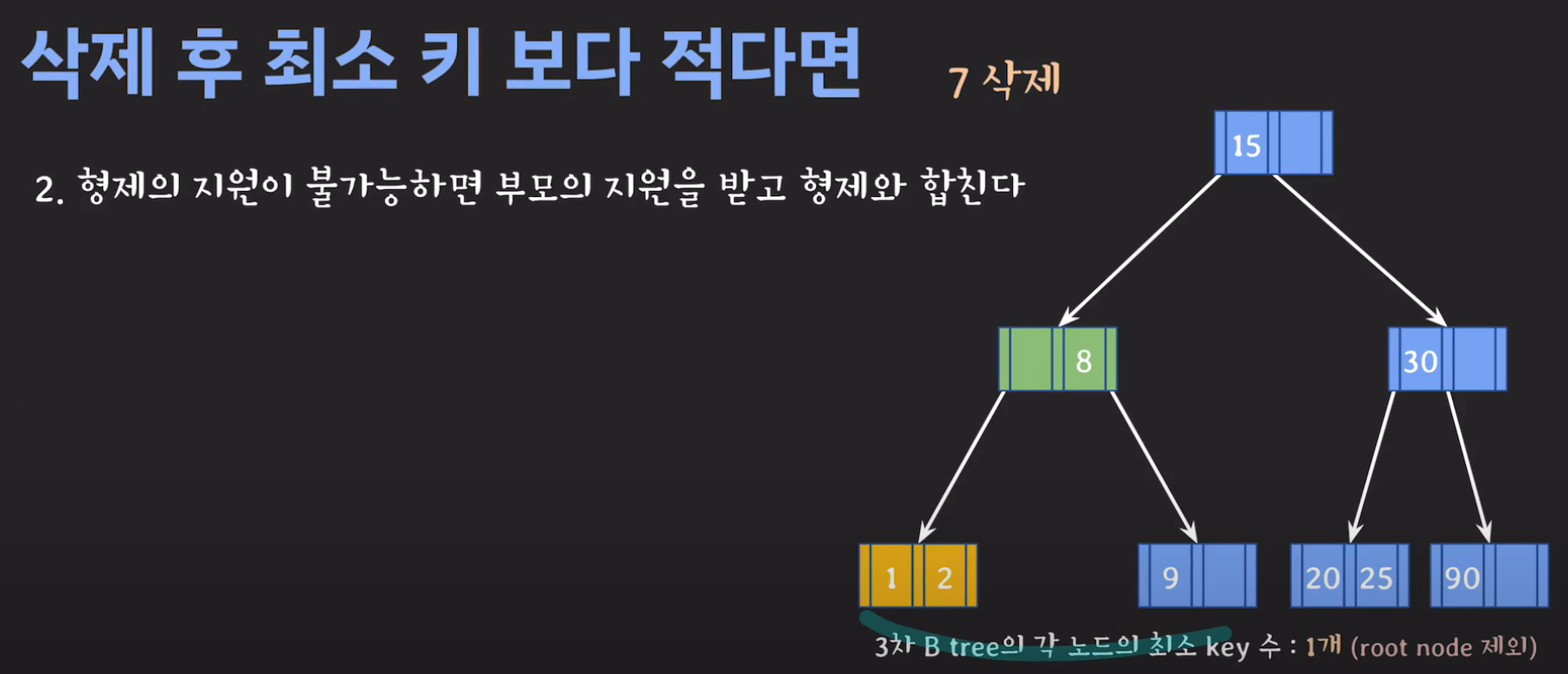
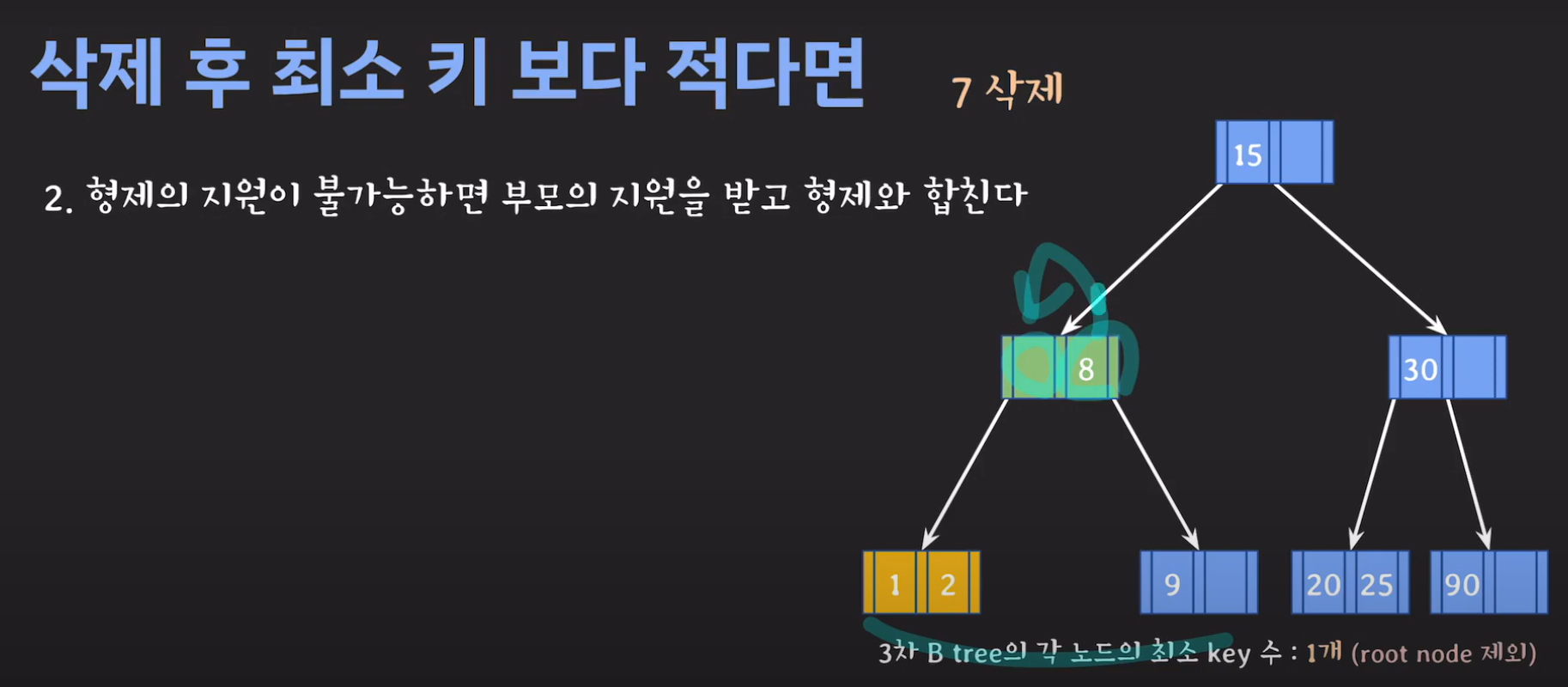
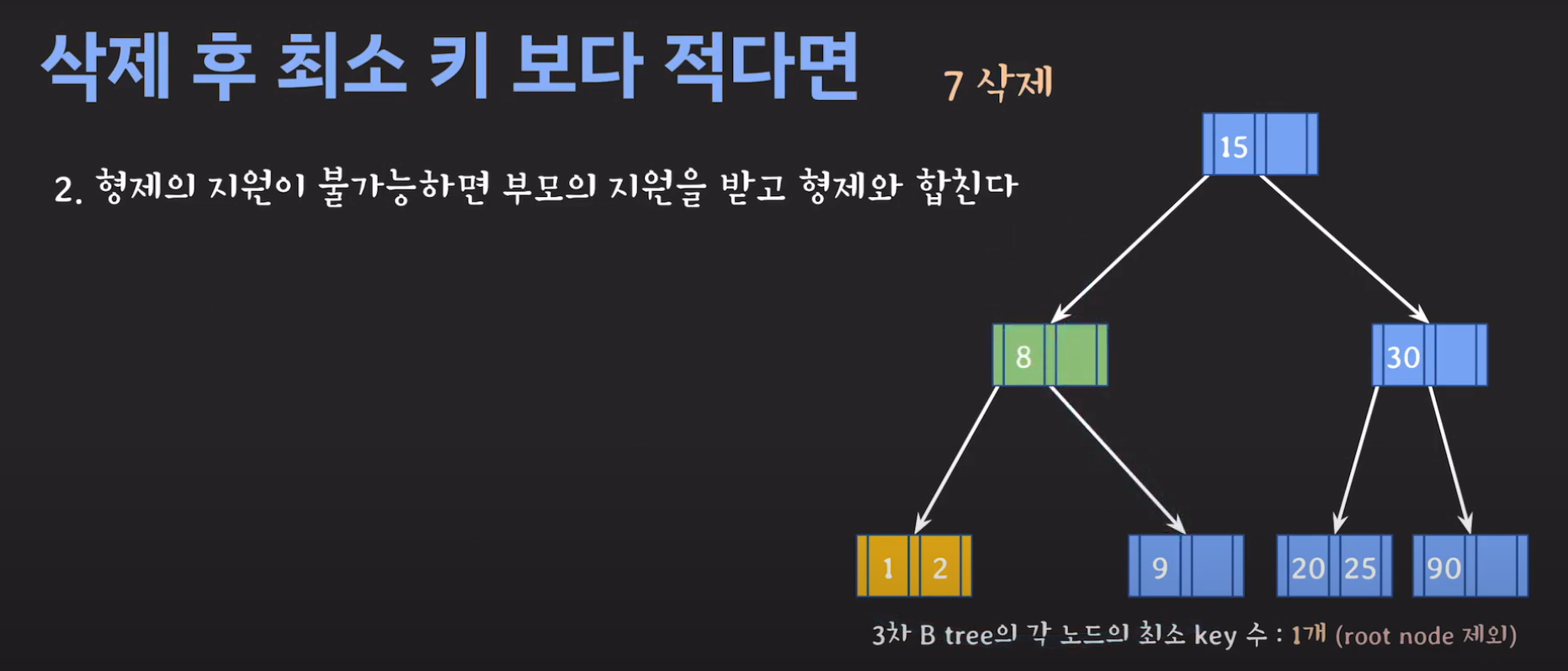
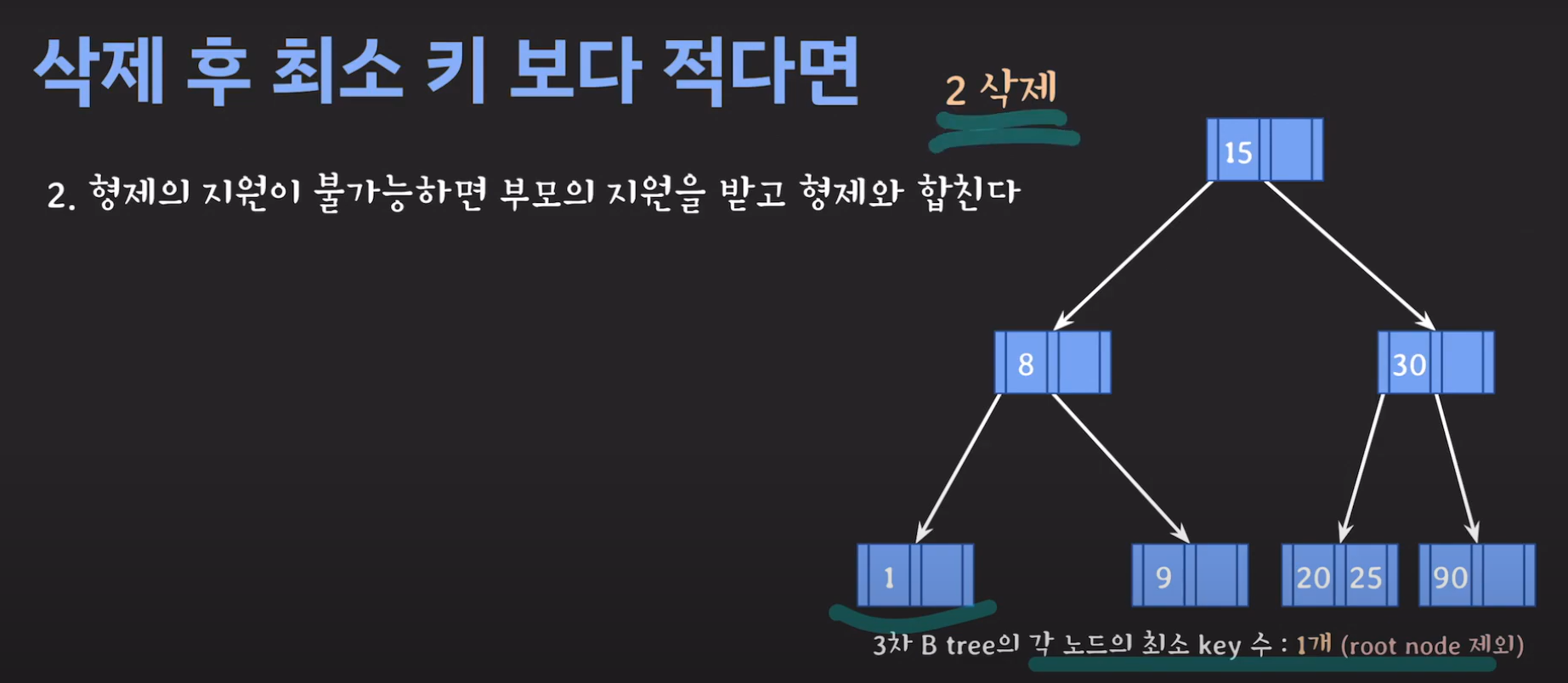
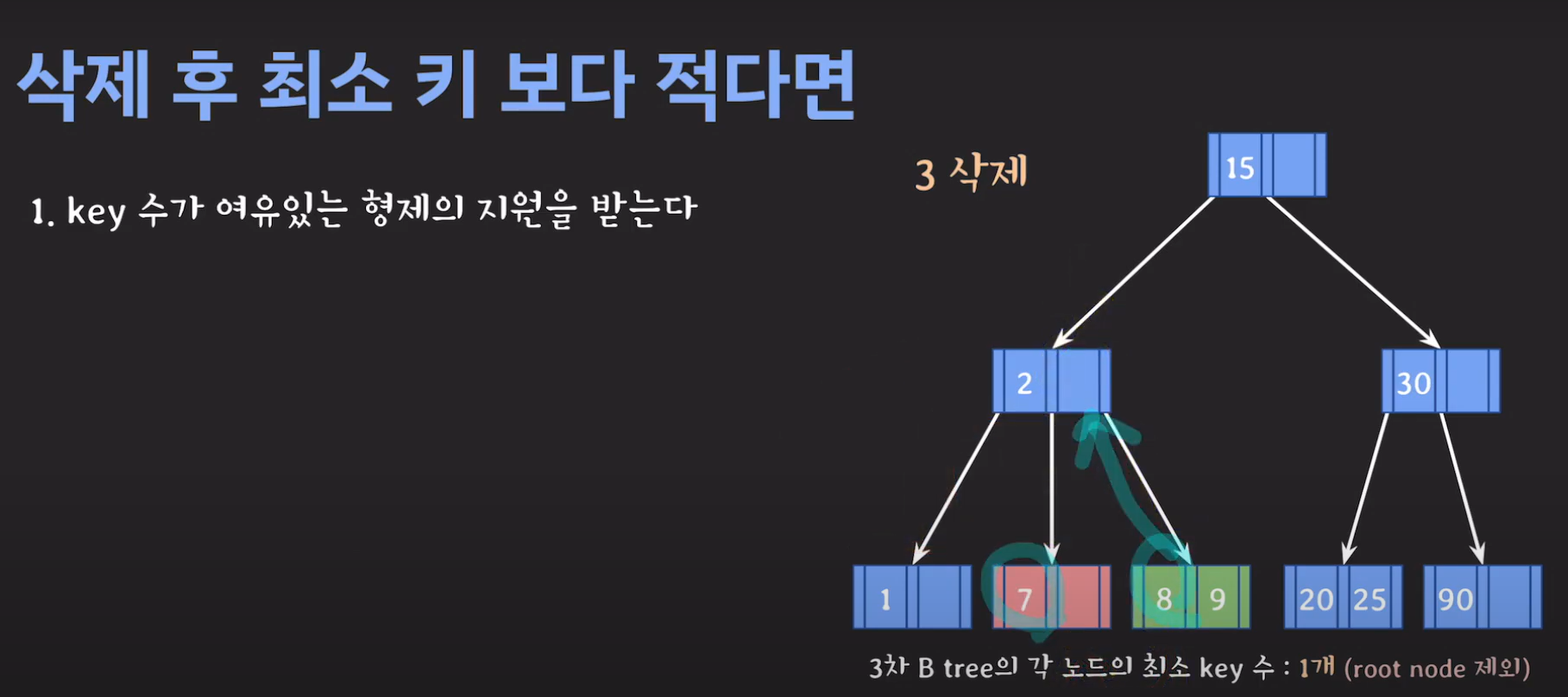
- 동생도 없고 형도 여유치 않으므로 부모님께 말씀드립시다.

- cf) 자식 사이의 있는 값을 줍니다.
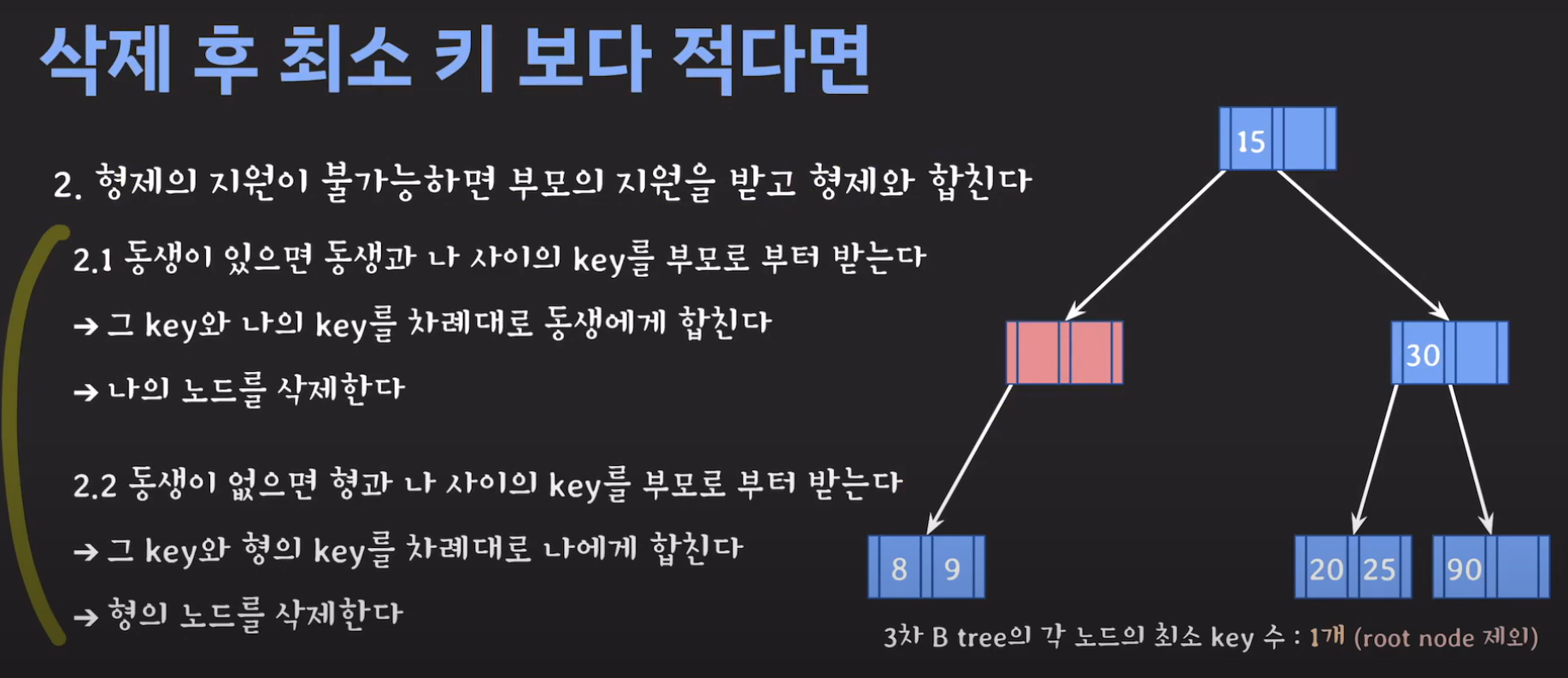
정리하면 다음과 같이 동작합니다.
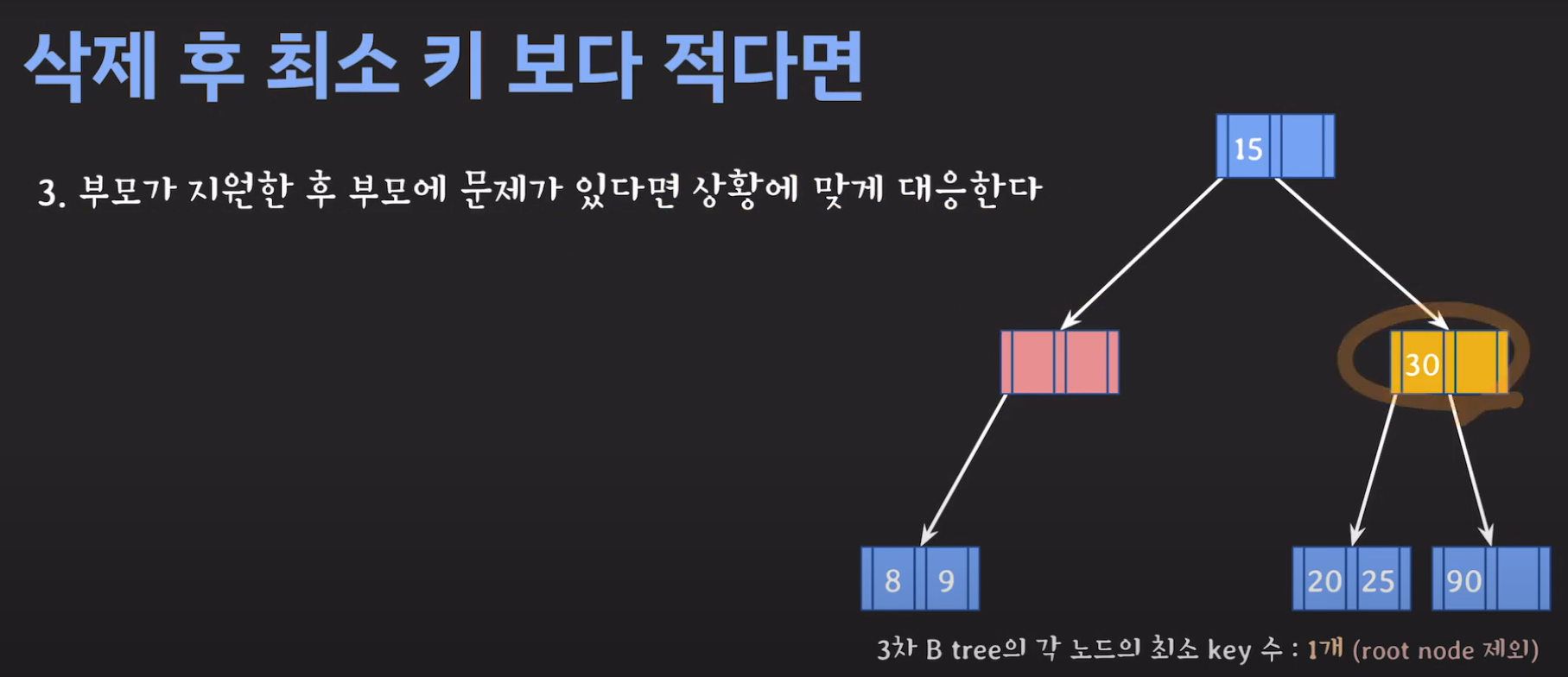
- 이번에도 동생은 없고 형도 여유치 않으므로 부모님께 말씀드립니다.
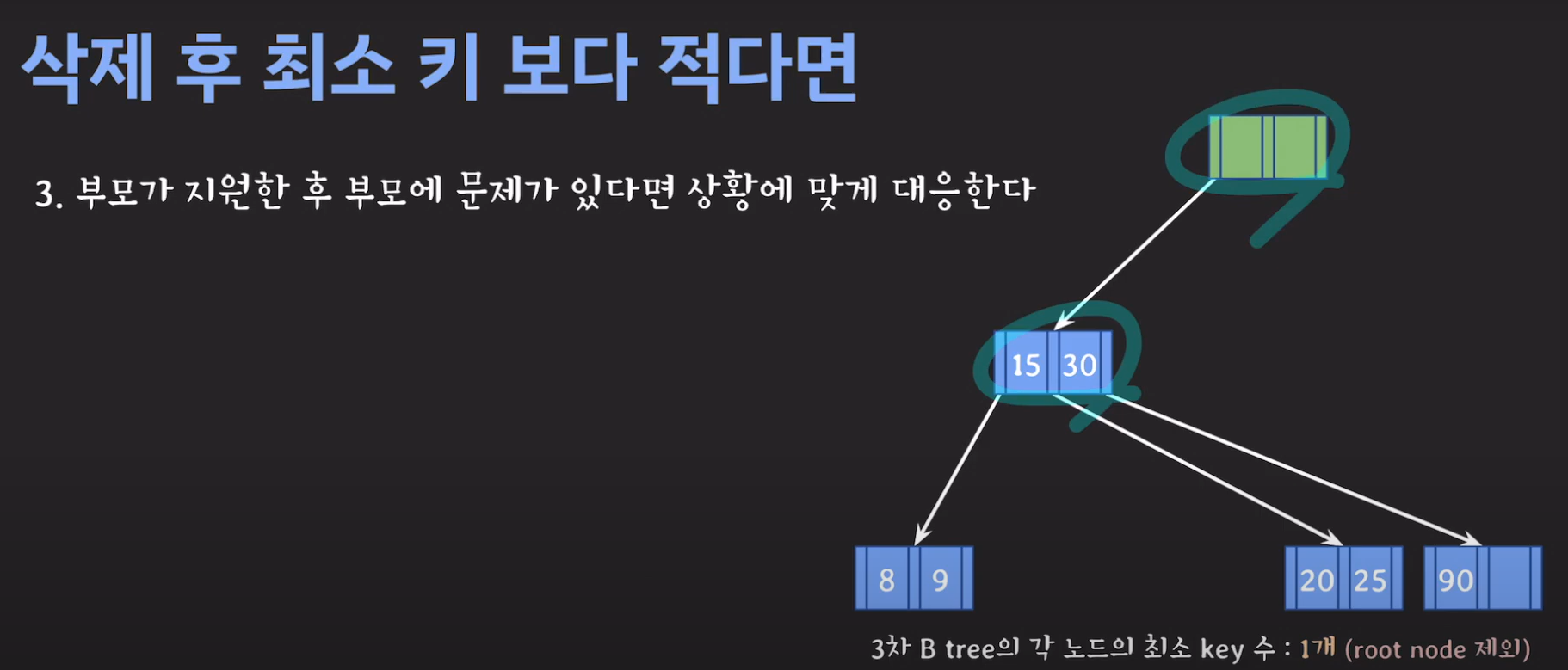
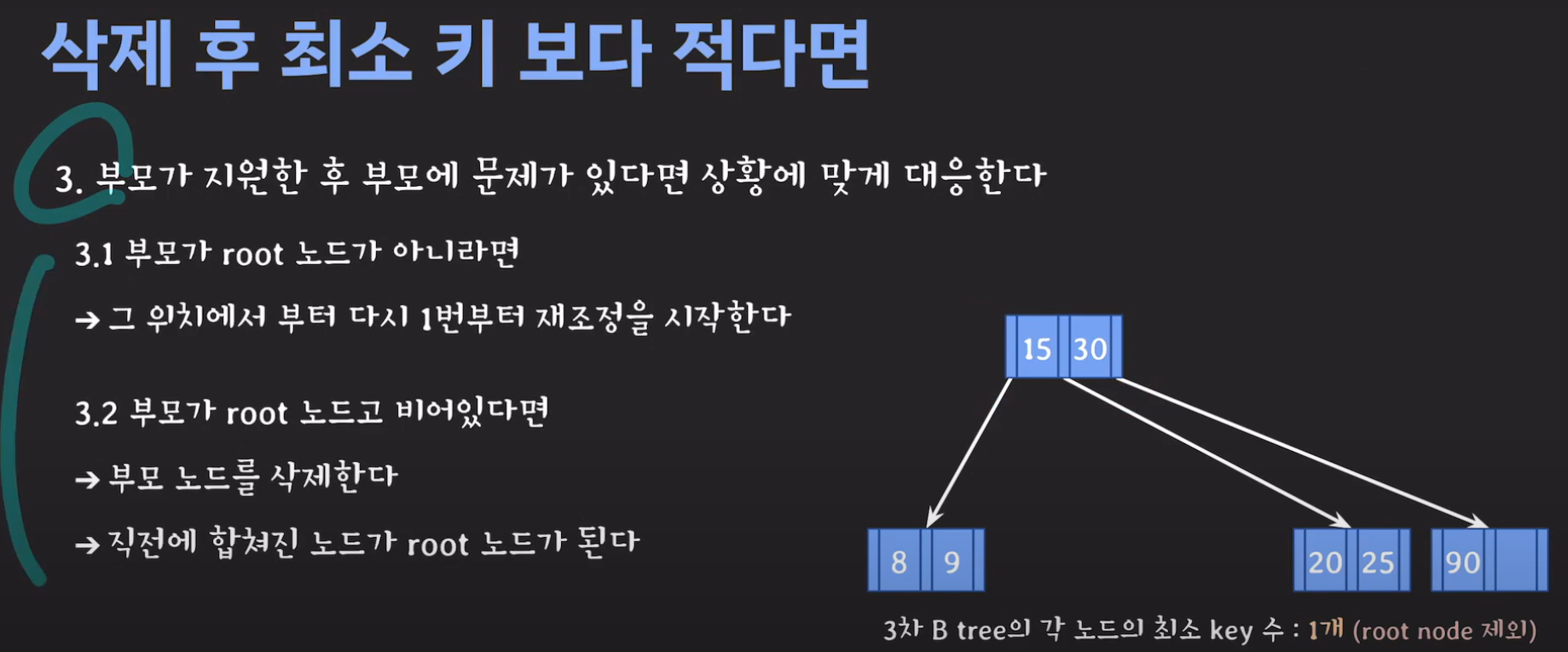
- 루트 노드에 아무것도 없을 경우는 그냥 삭제해주면 됩니다.
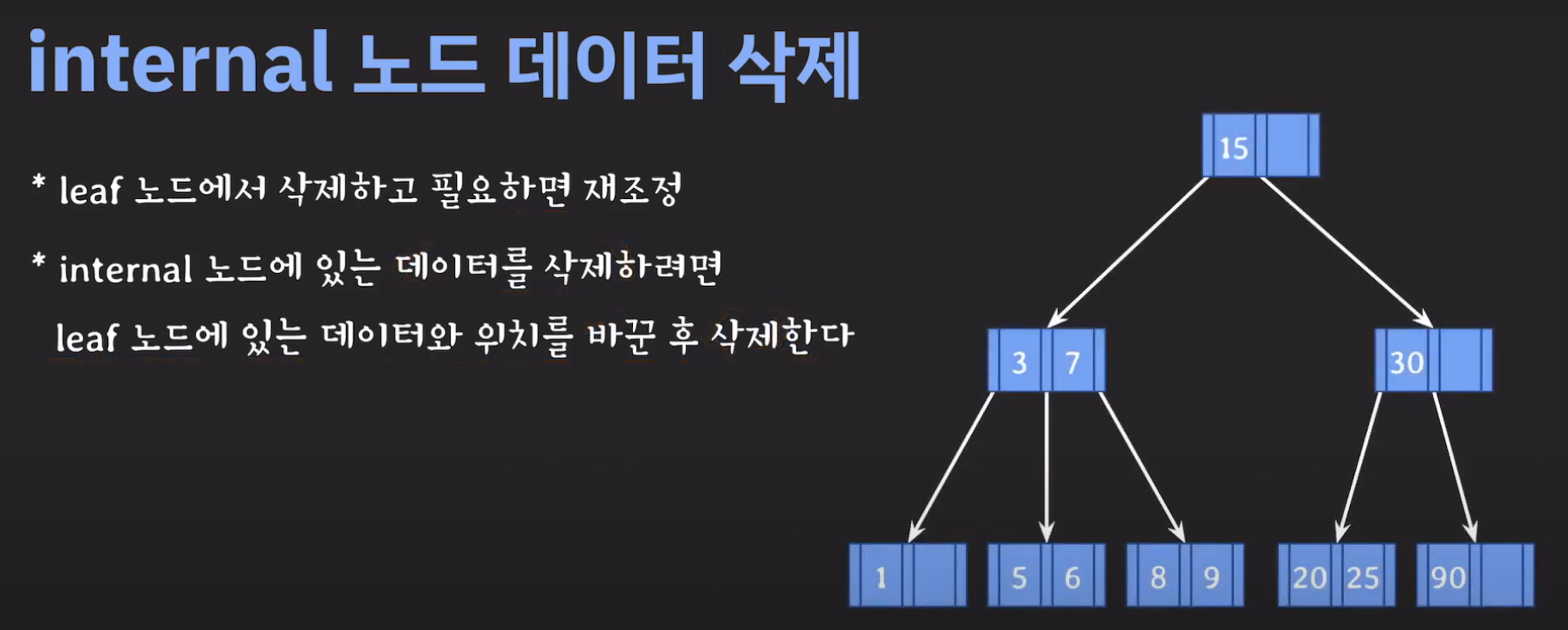
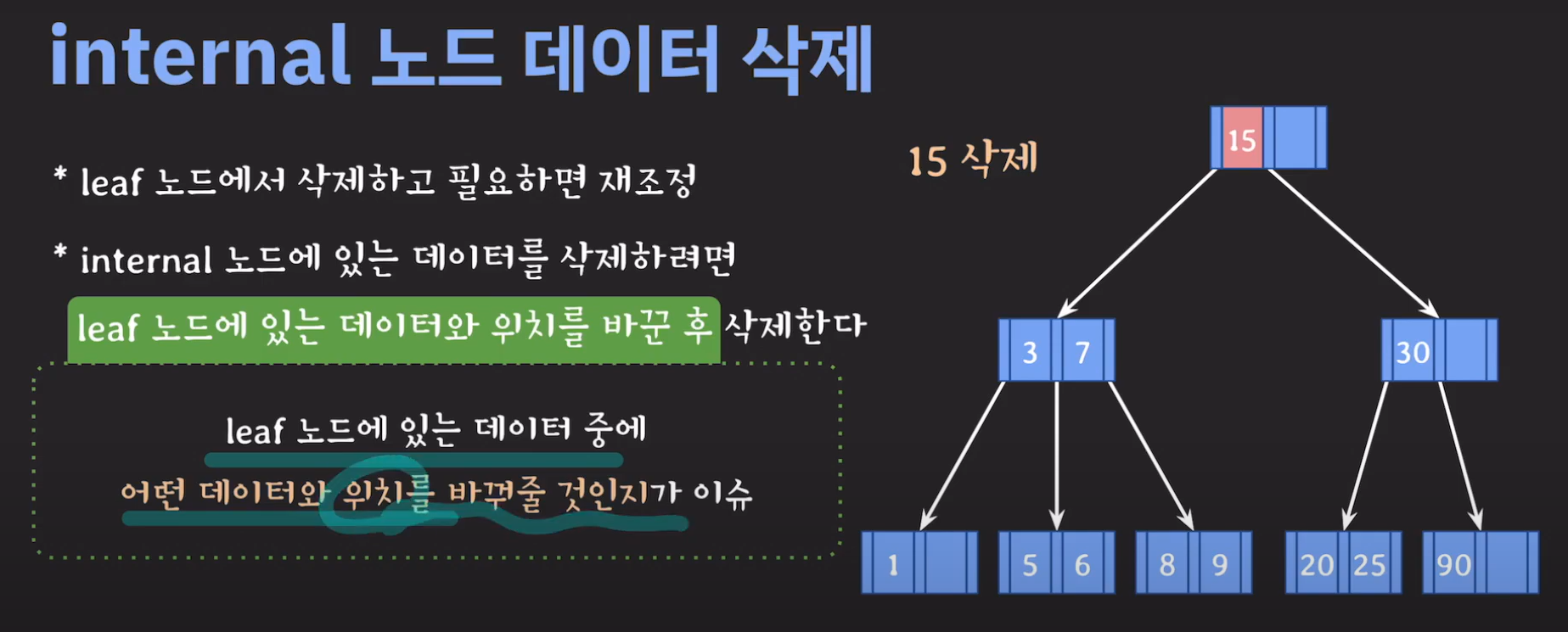
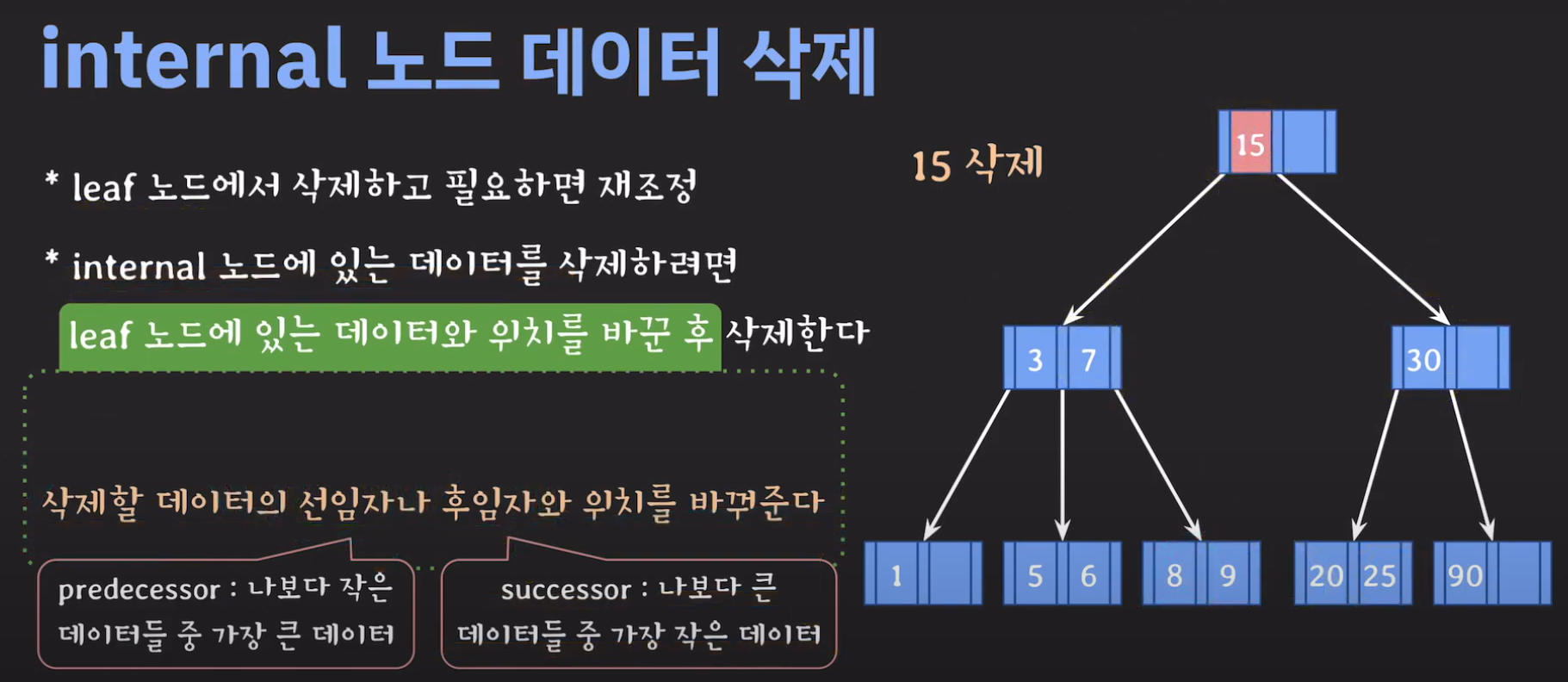
그럼 선임자나 후임자가 리프 노드에 있는지 확인만 해보면 됩니다. 이를 간단히 증명해봅시다.
트리의 가장 큰 값은 오른쪽으로 계속 이동해야 나올겁니다. (Binary Tree 특징) 따라서 선임자의 경우 왼쪽 서브트리로 이동후 계속 오른쪽 노드로 이동해서 리프노드까지 도달 할 경우 선임자인것 을 알 수 있습니다.
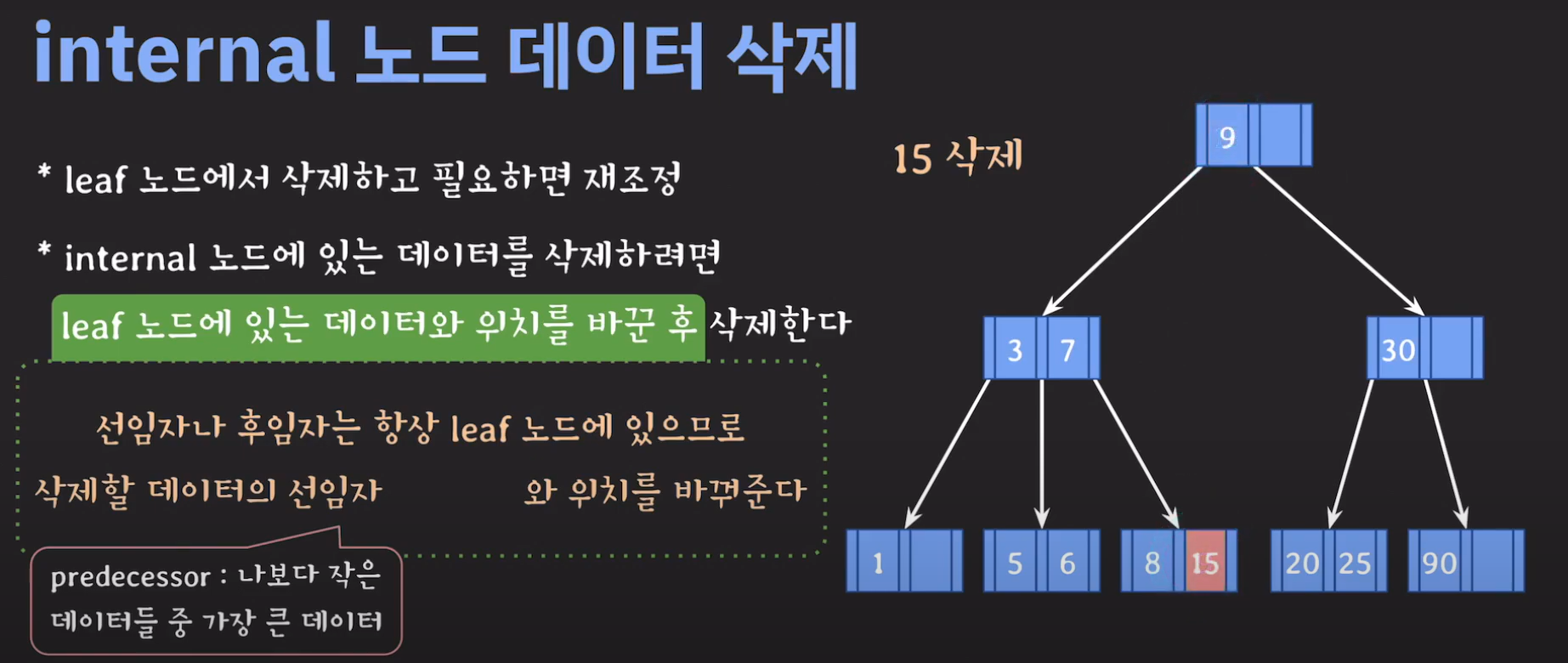
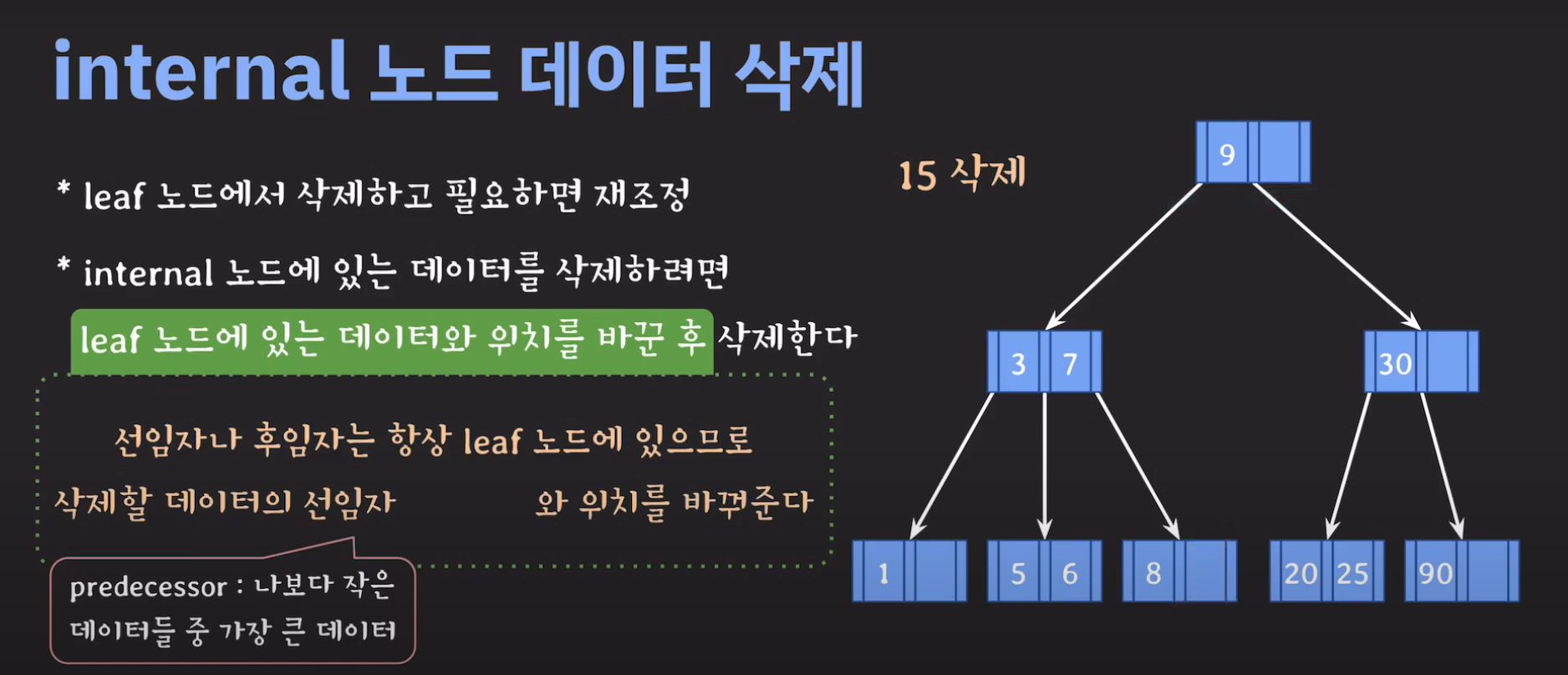
정리하면 다음과 같습니다.

5차 B Tree를 예시로 마무리해봅시다.
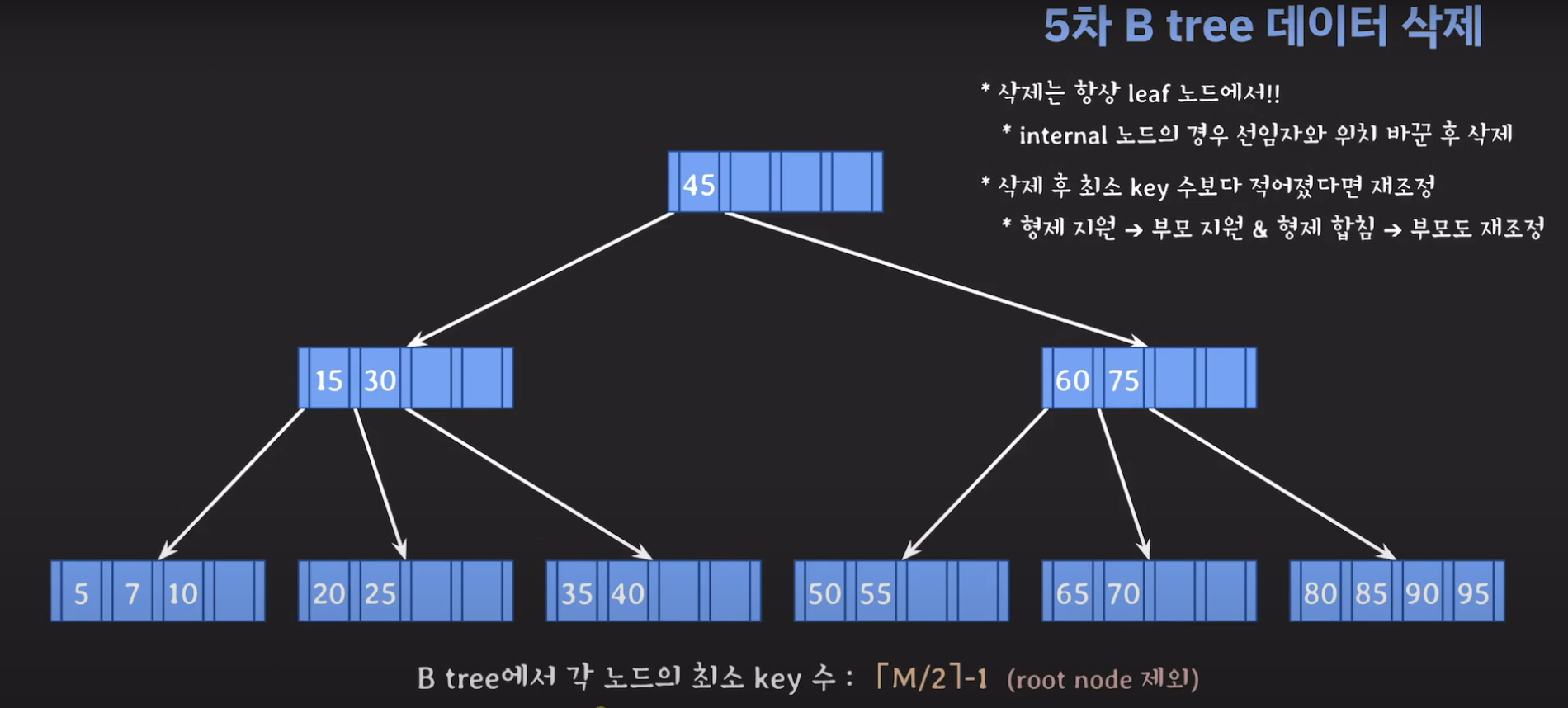
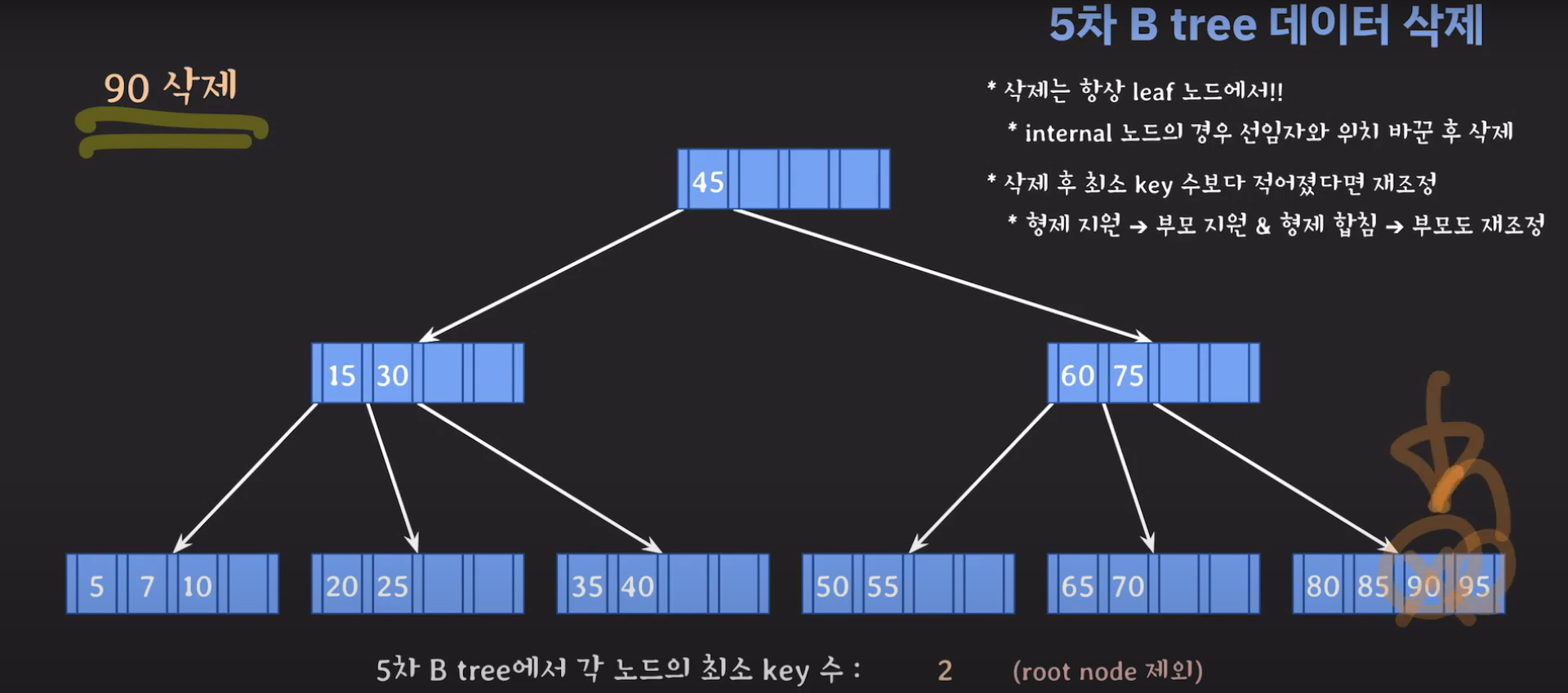
75는 internal 노드이므로 선임자과 바꿔줍시다.
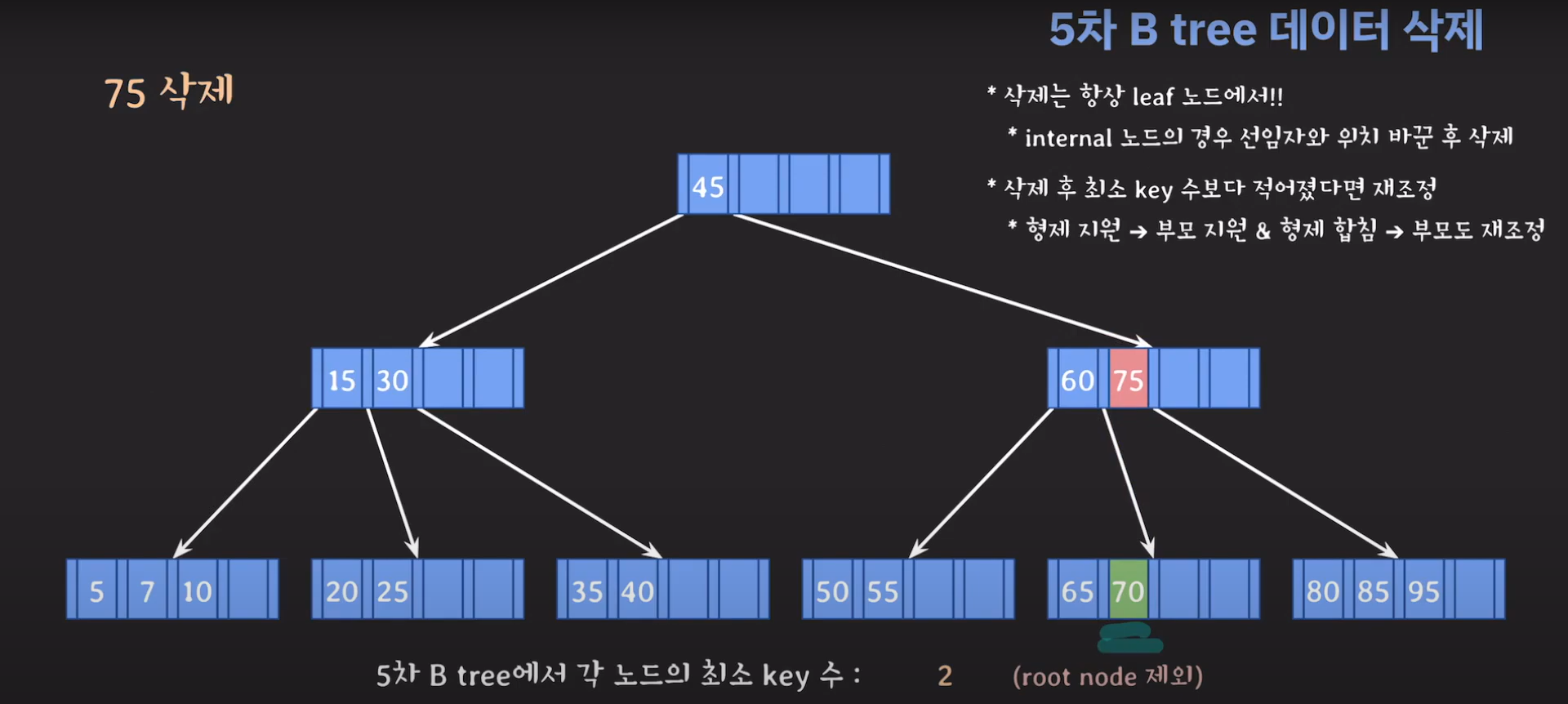
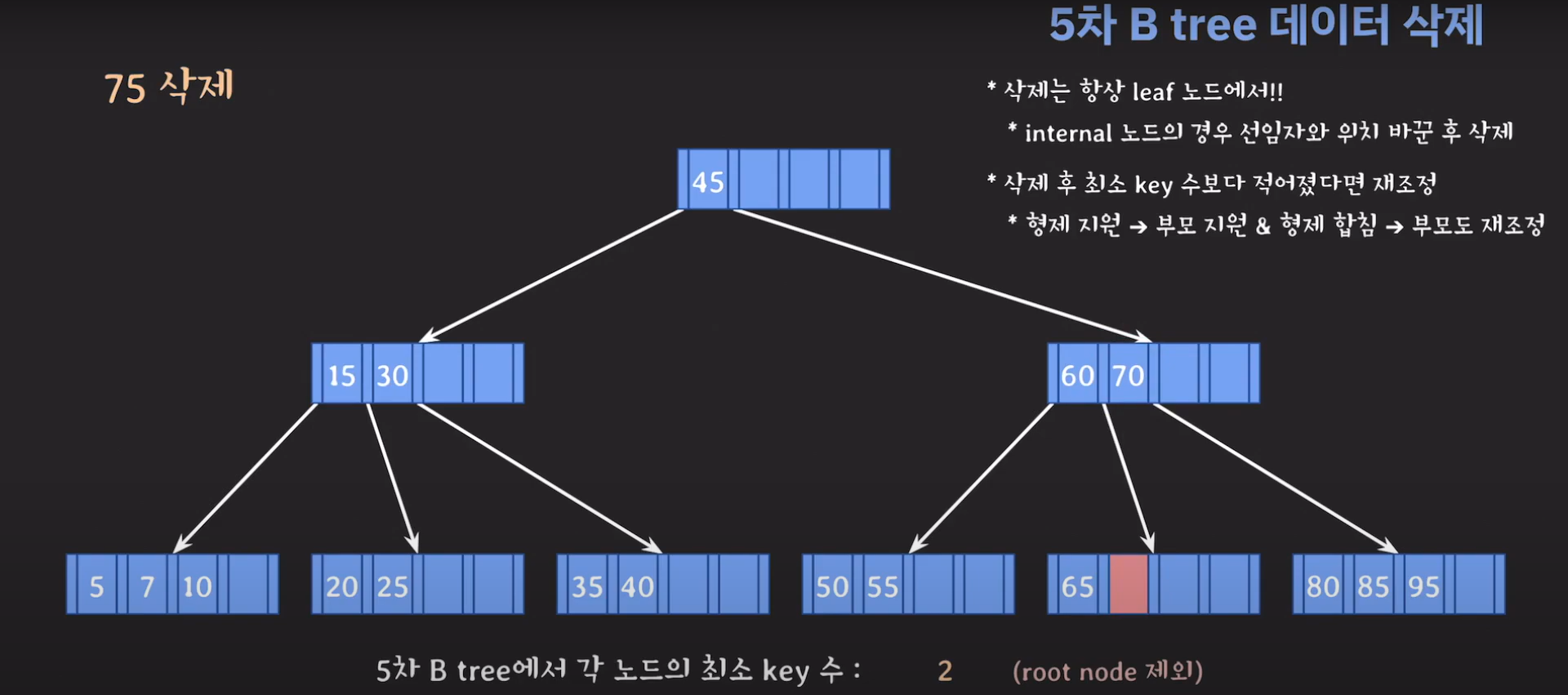
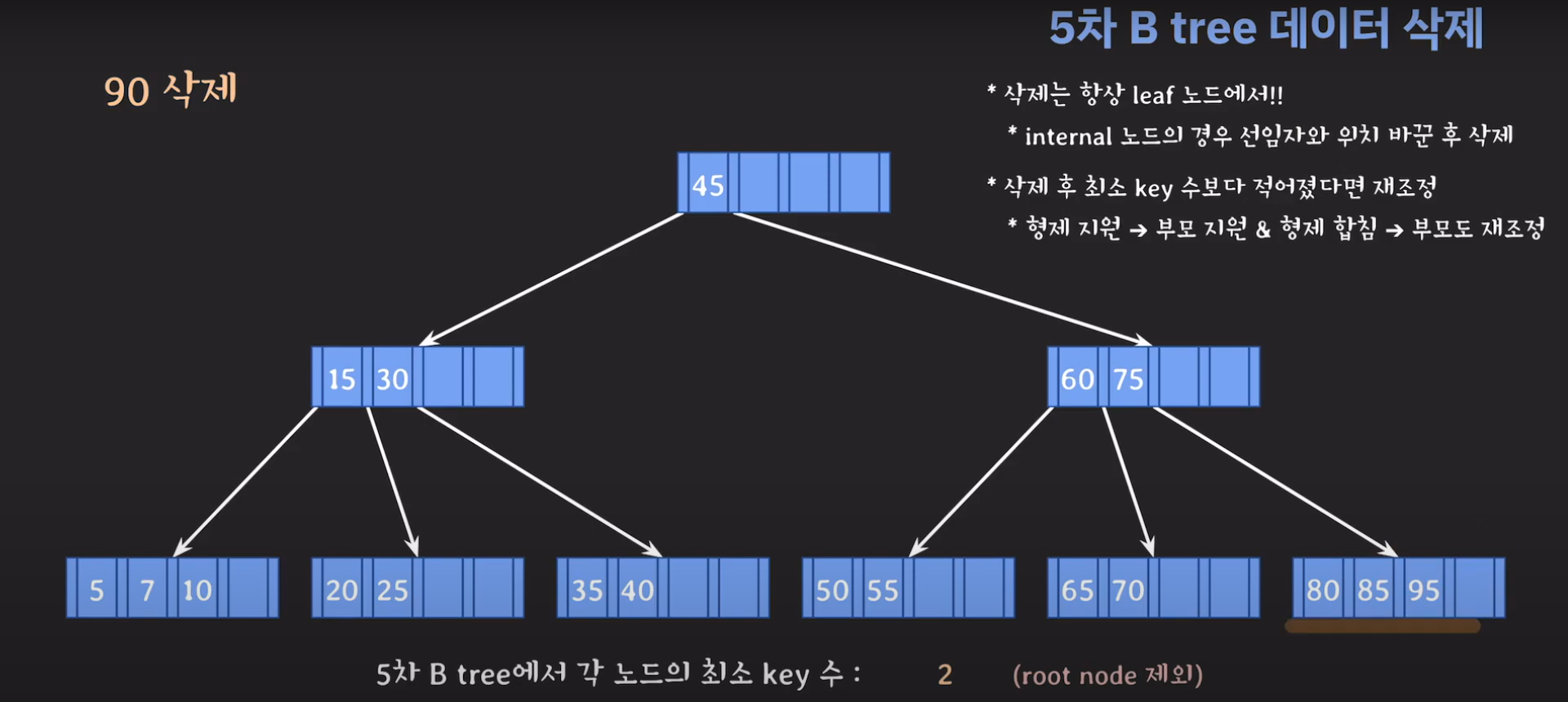
75를 삭제하고 보니까 key가 한 개이며 최소 2개의 키를 가지고 있어야 하는 조건을 만족하지 못합니다.
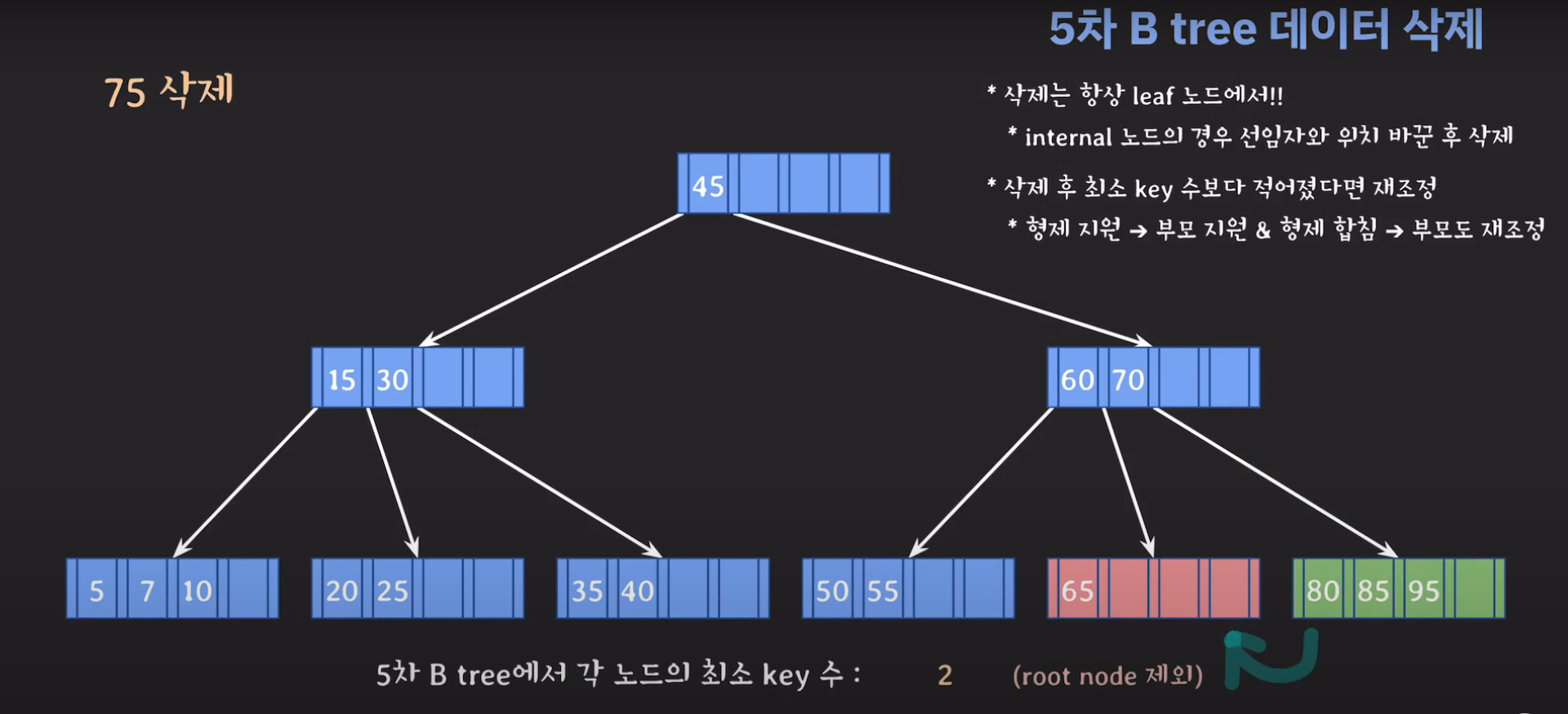
동생은 여유치 않으니 형한테 도움을 받아봅시다.
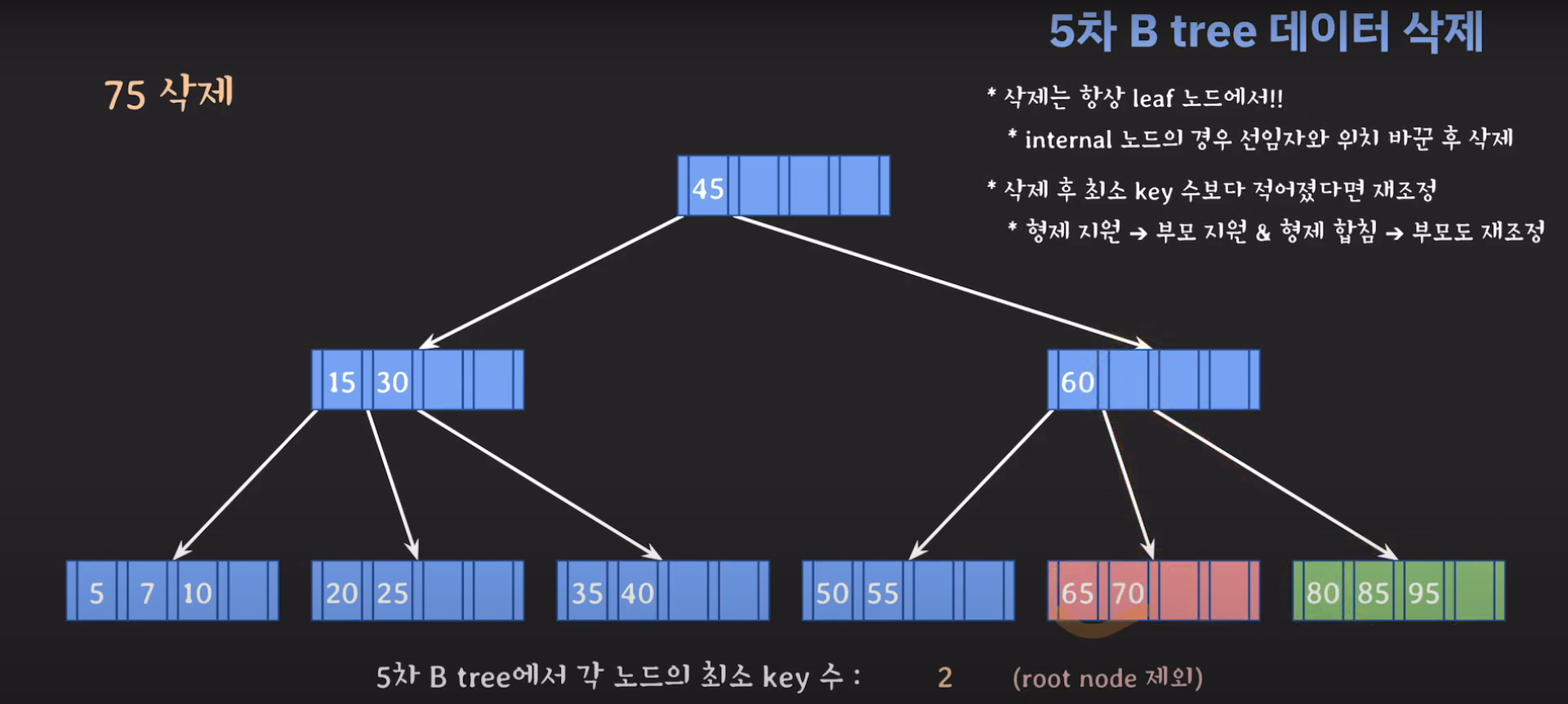
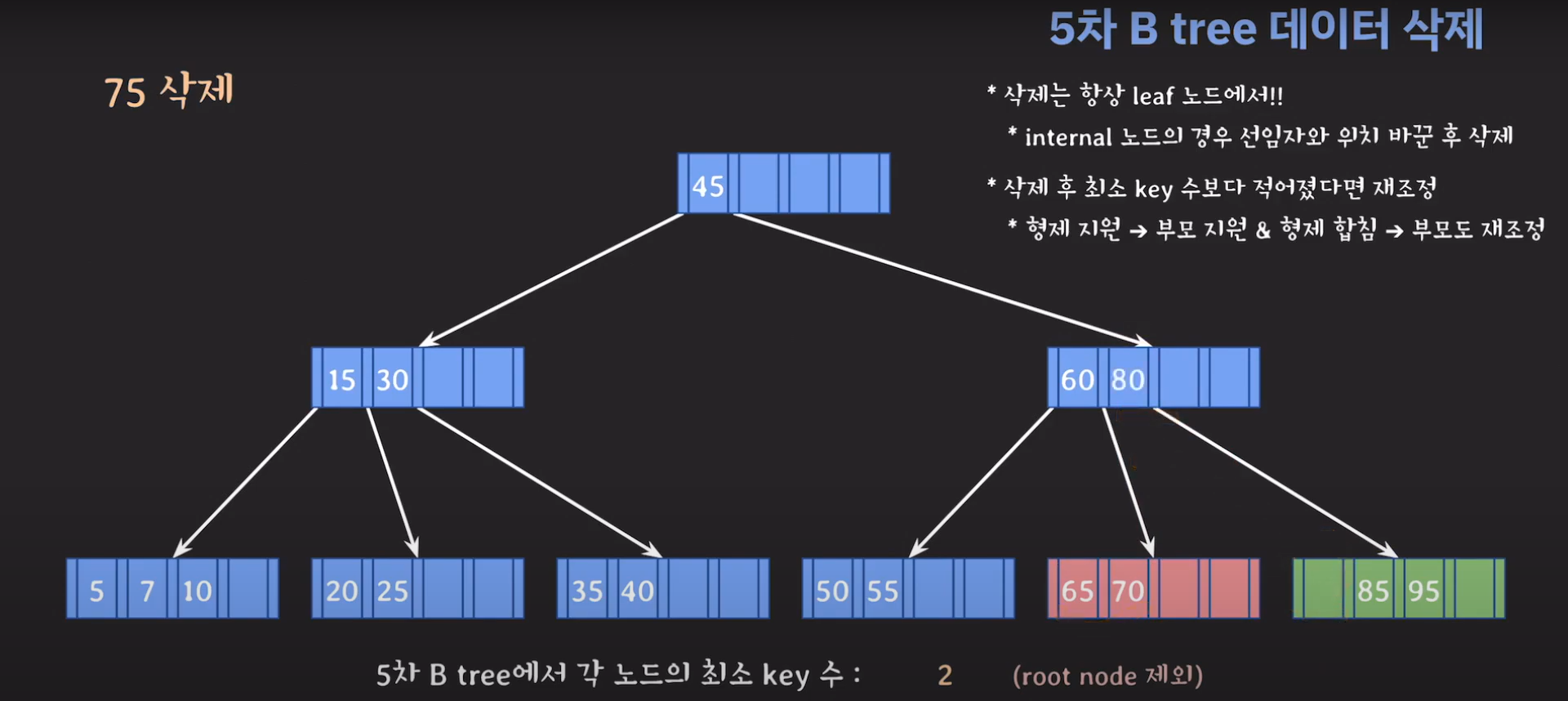
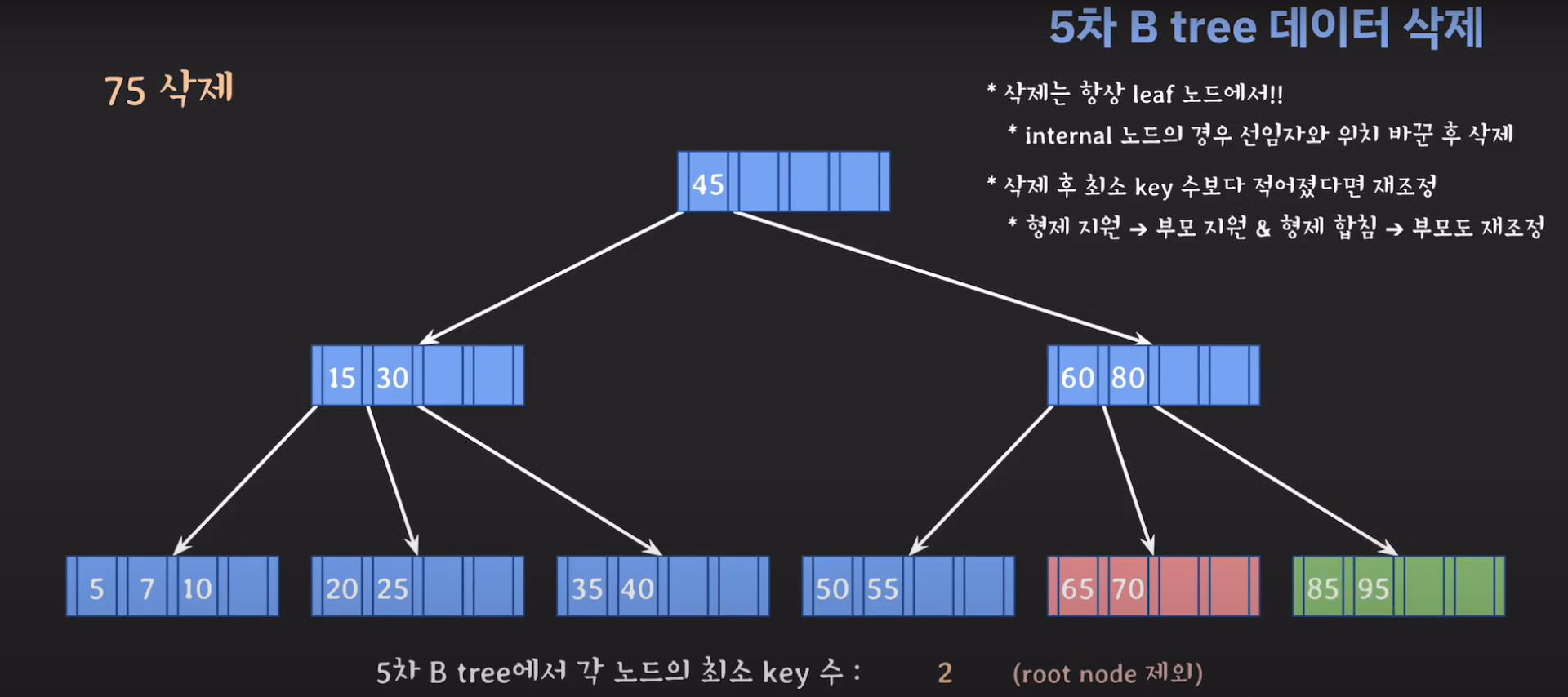
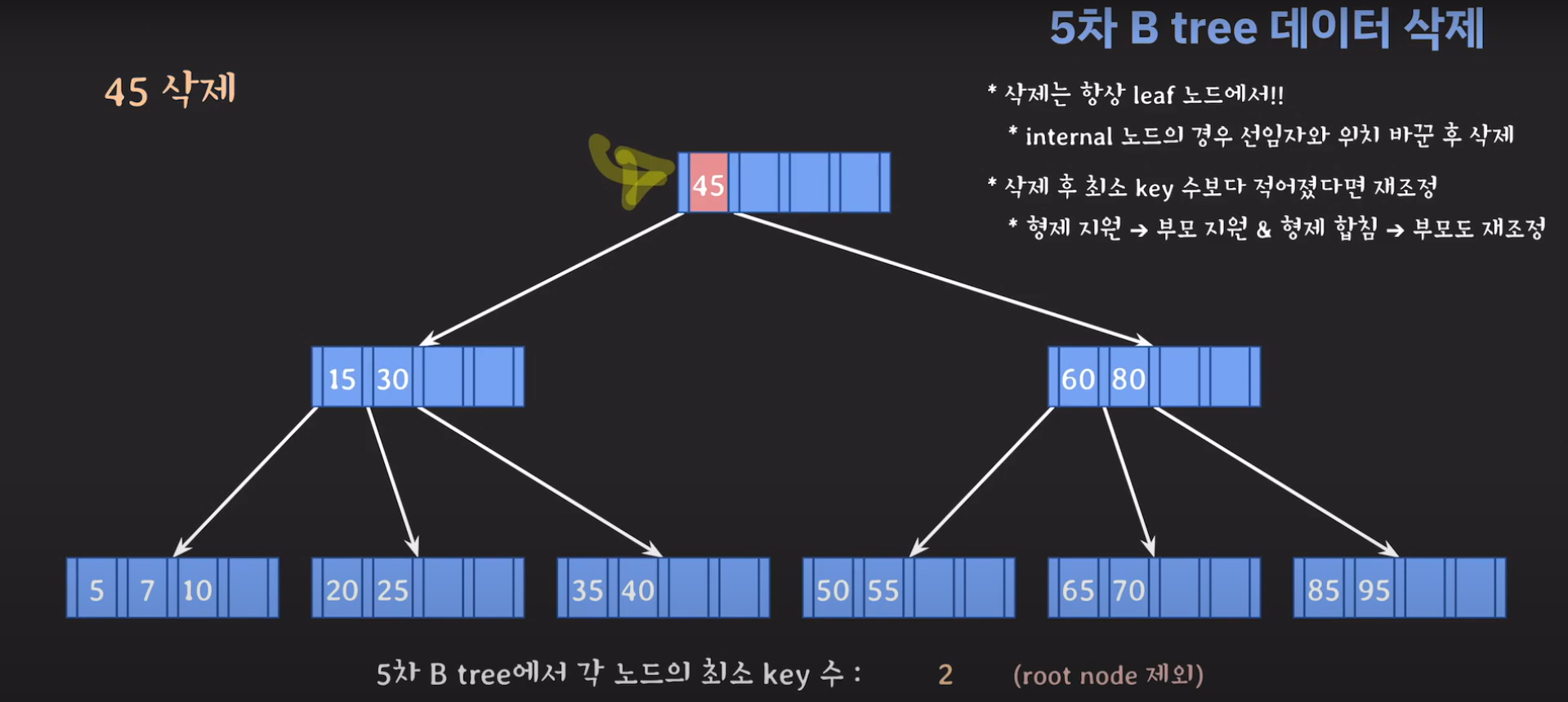
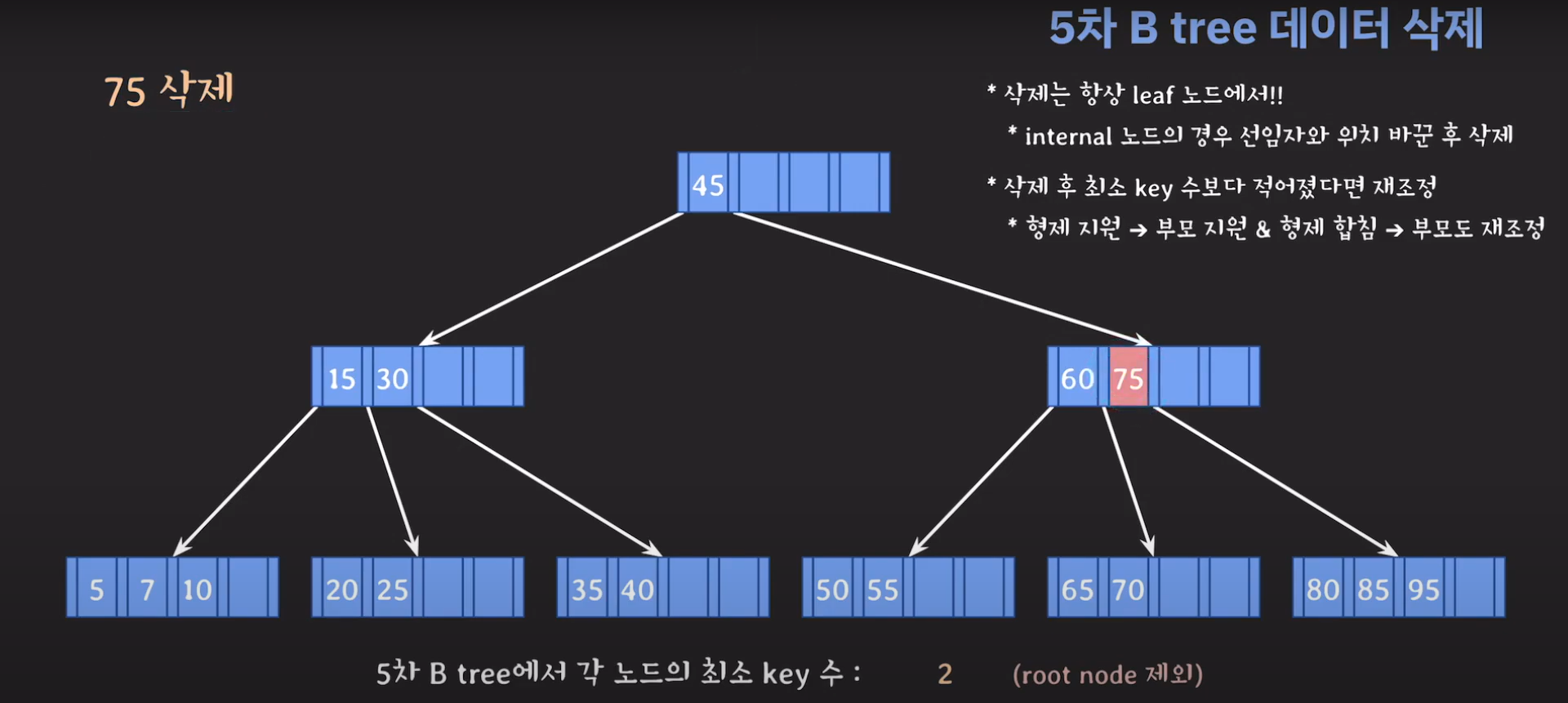
45는 internal 노드이므로 선임자와 바꿔줍시다.
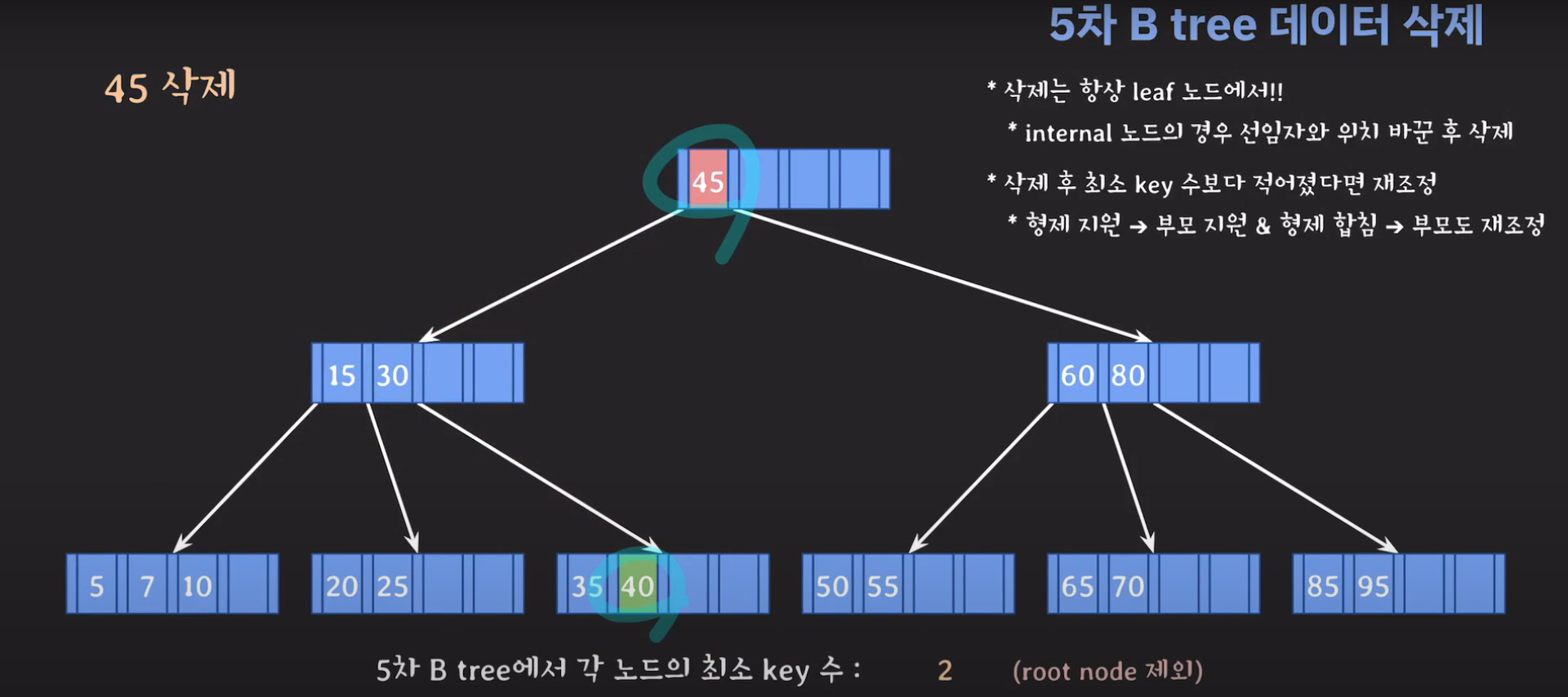
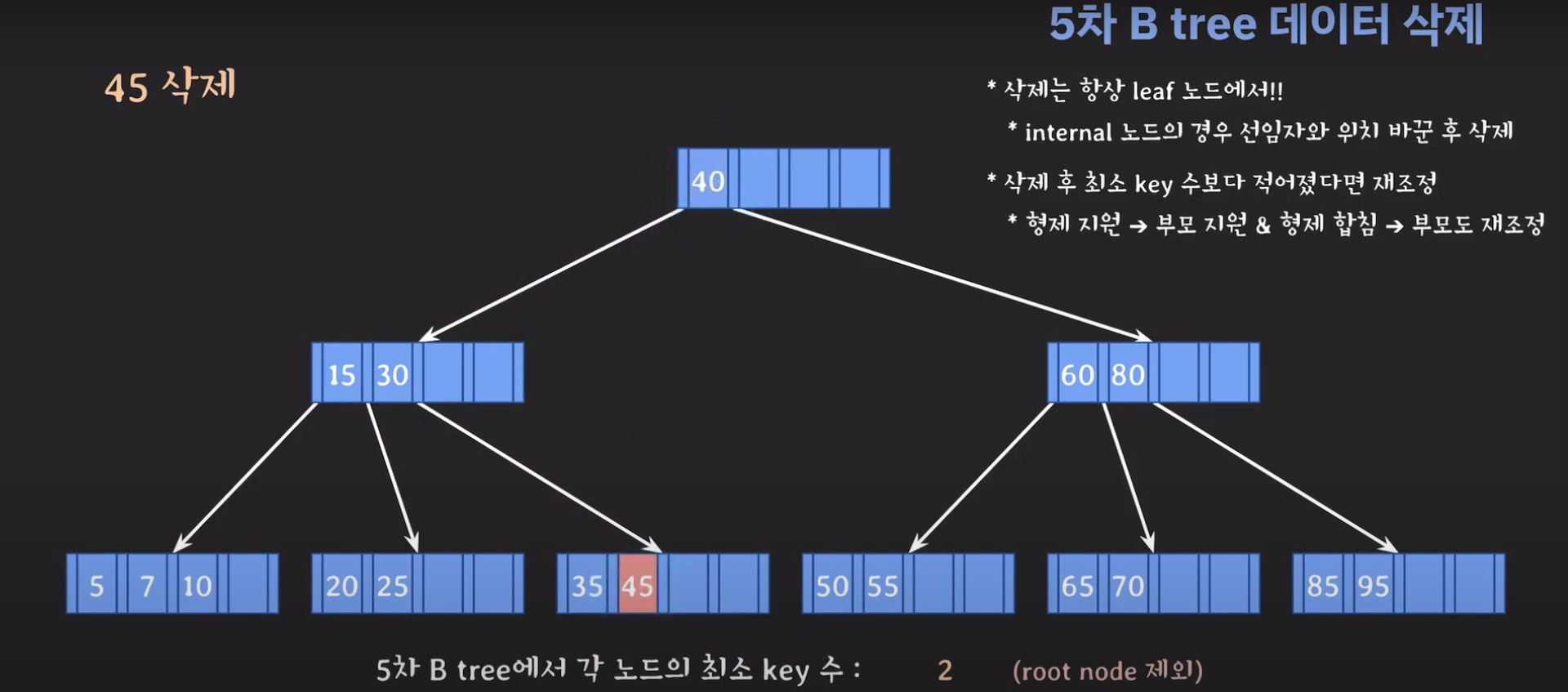
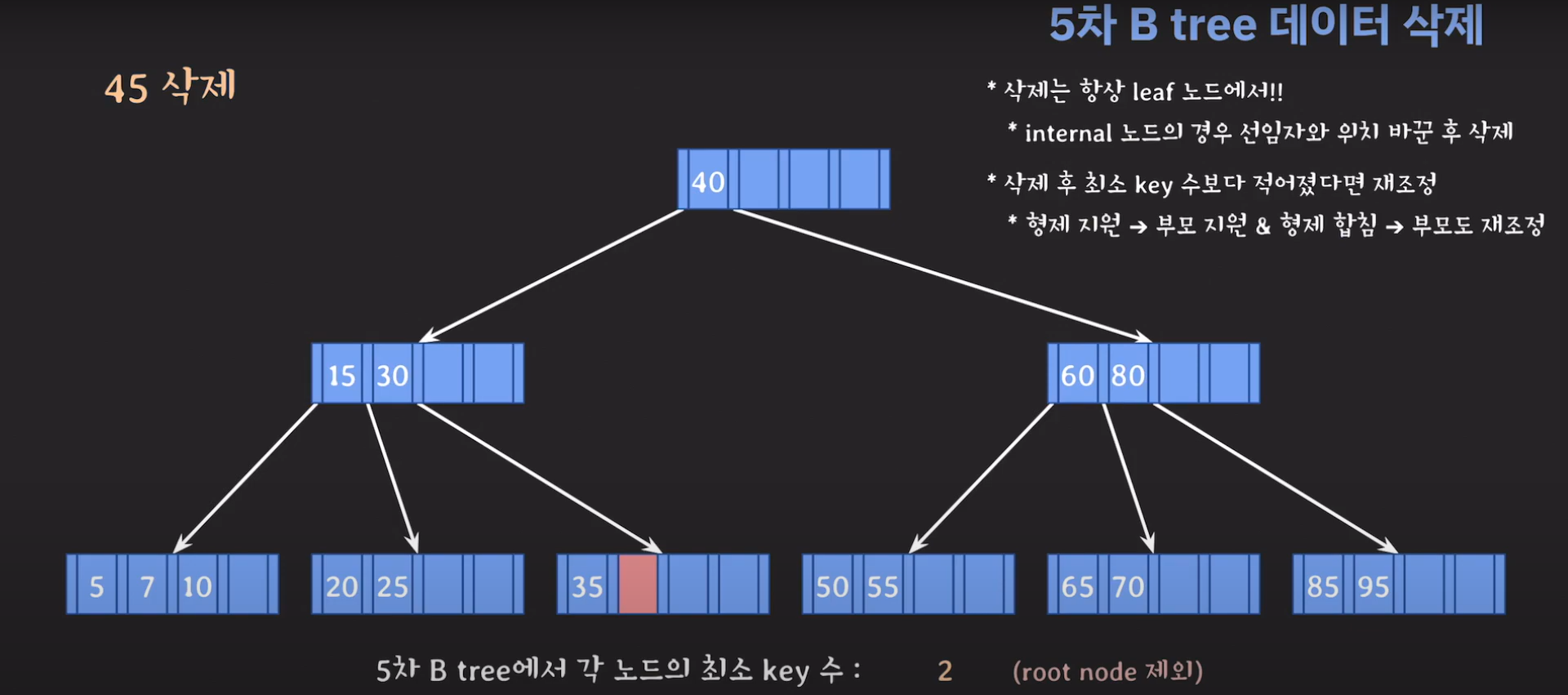
이때 최소 key 조건을 만족하지 않으므로 재배치 해주어야 합니다. 형은 없고 동생은 여유치 않으므로 부모님께 말씀드려야 합니다. 동생과의 사이값(30)을 부모님으로부터 받고 동생쪽으로 합칩니다.
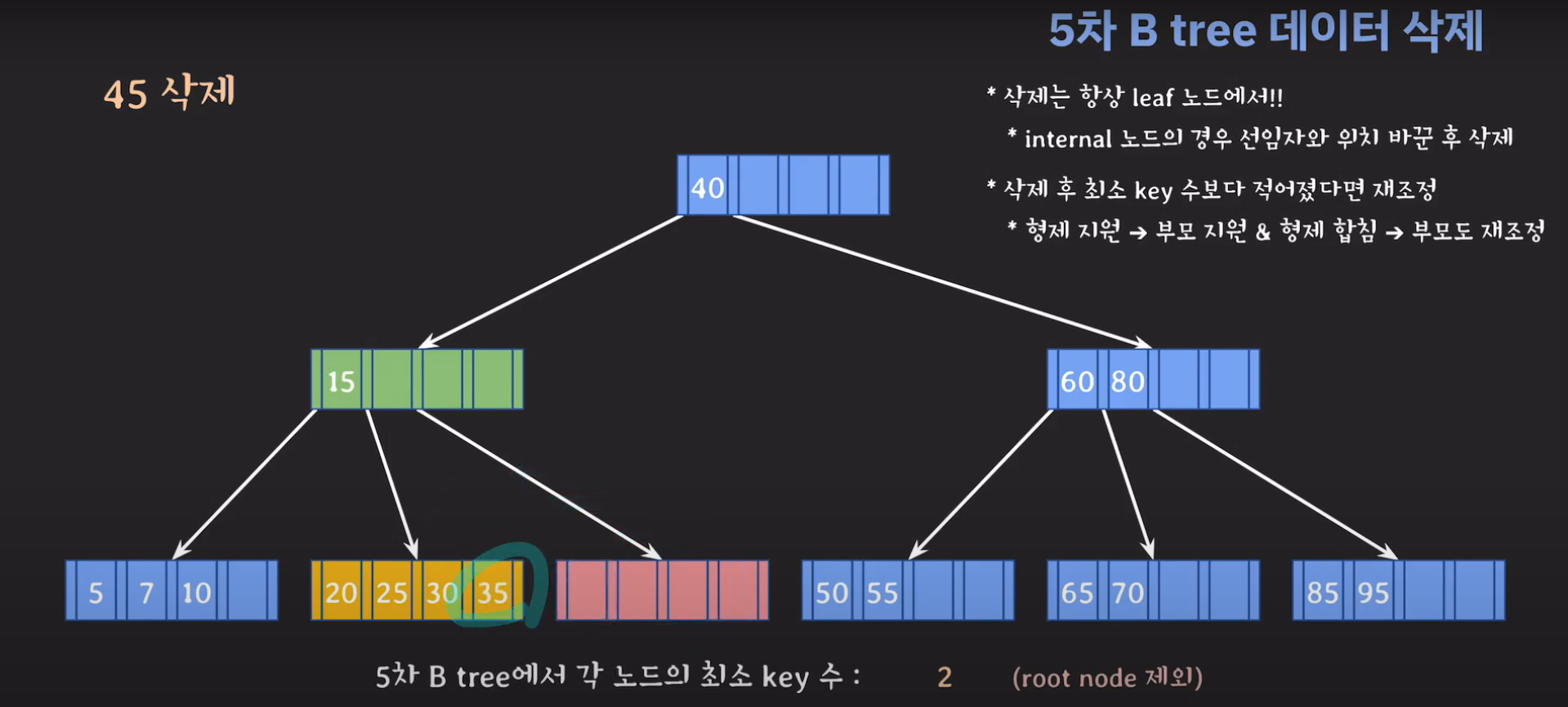
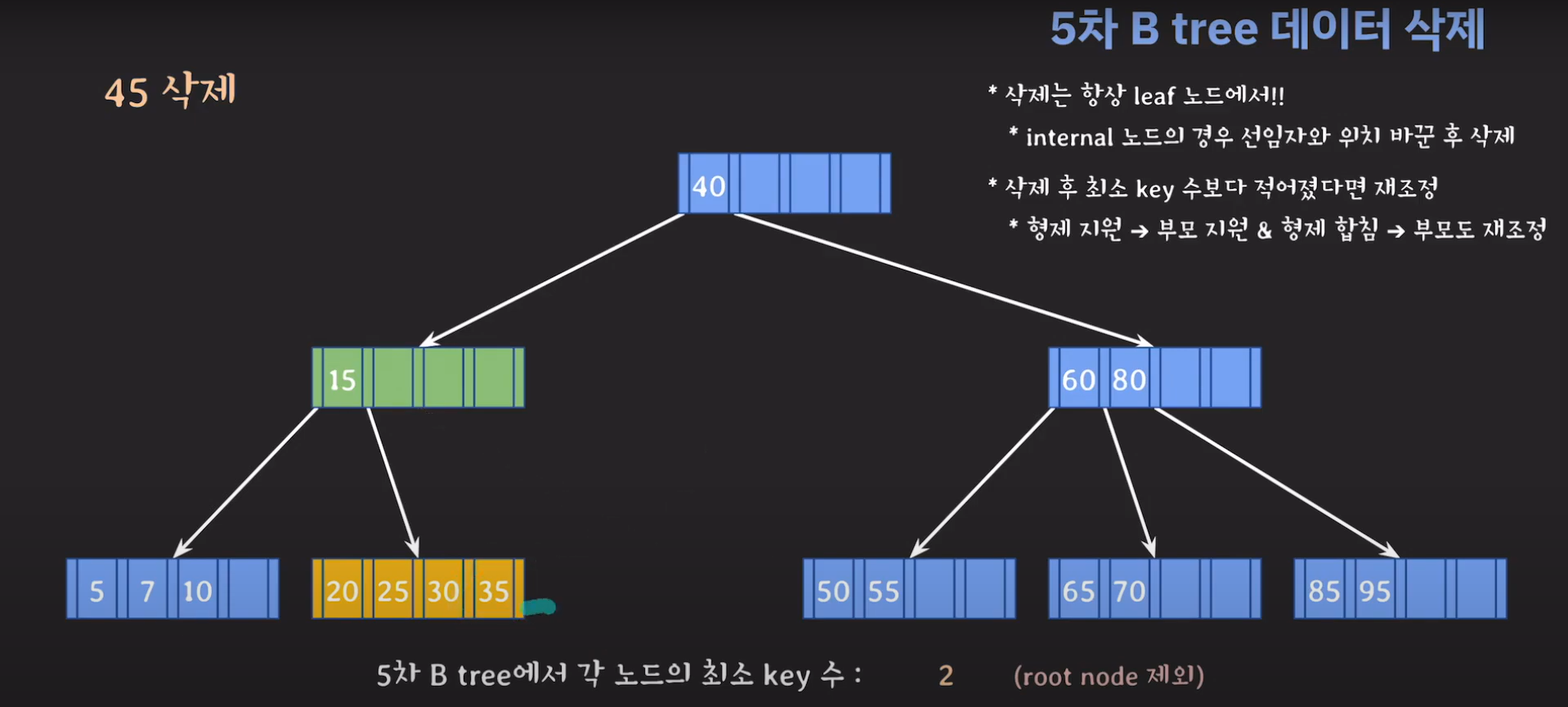
부모의 데이터 수가 조건을 만족하지 않는것을 알 수 있습니다. 이 경우 역시 재배치를 해주어야 합니다.
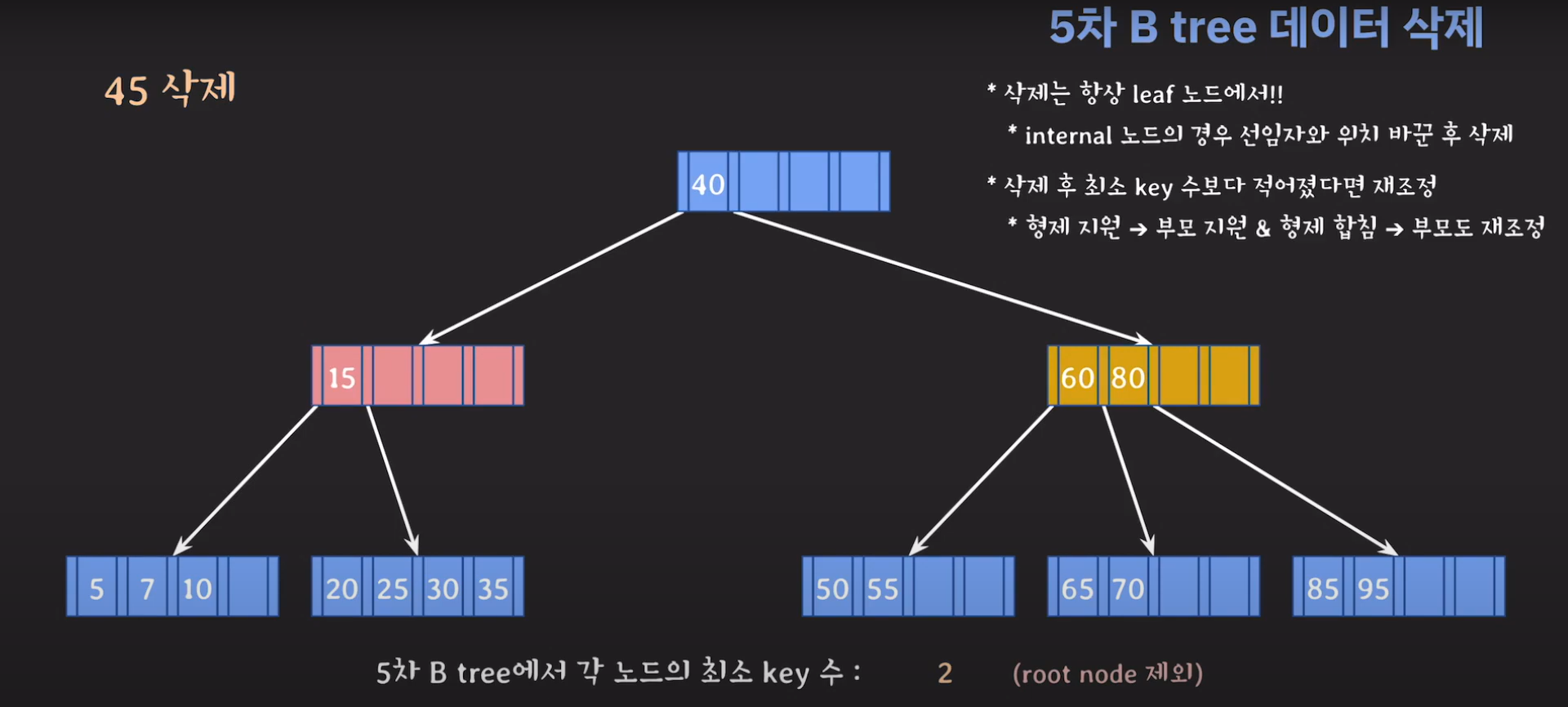
동생은 없고 형은 여유치 않으므로 부모님께 말씀드려야 합니다.
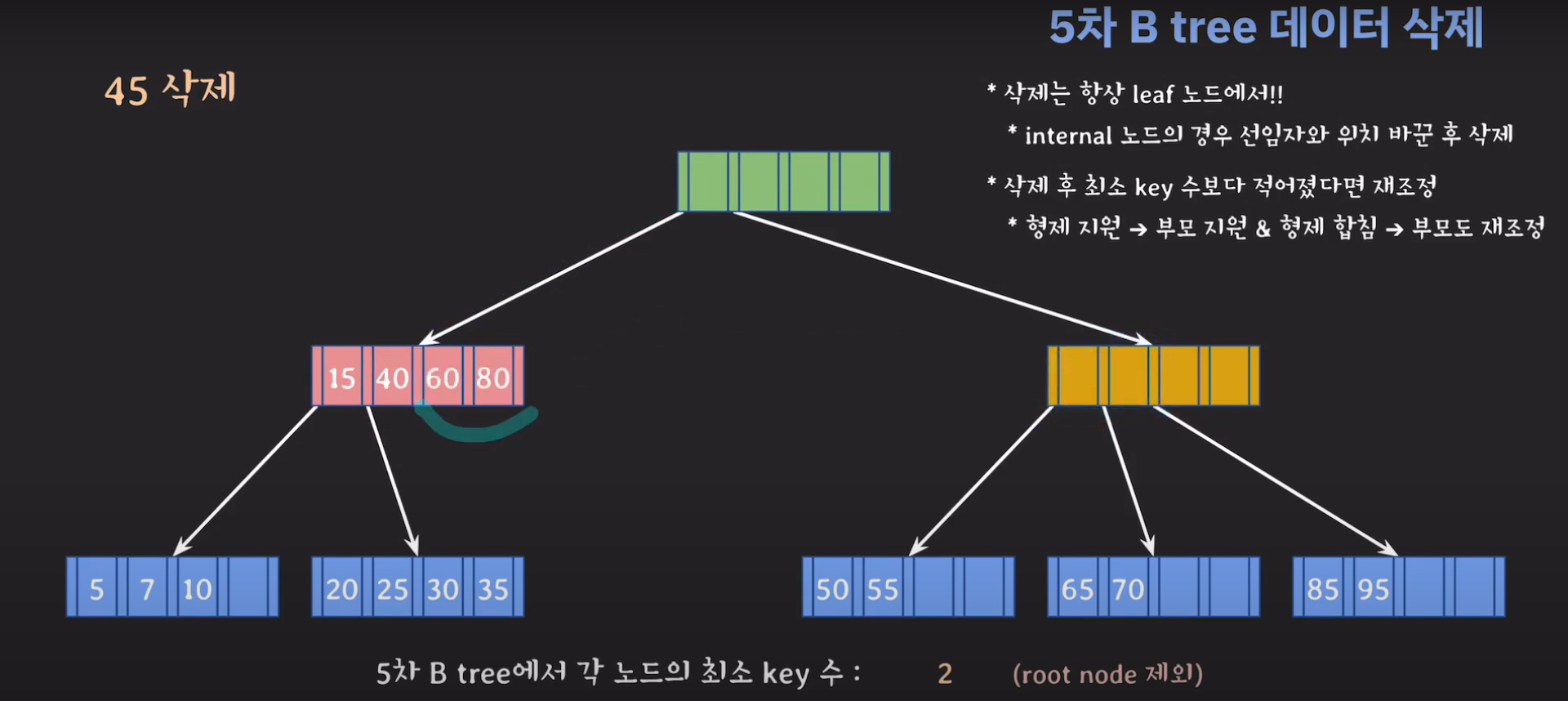
부모님으로부터 데이터를 받고 데이터를 왼쪽으로 합쳐주면 위와 같습니다. 이때 값을 옮겼으므로 포인터들로 옮겨주면 아래와 같습니다.
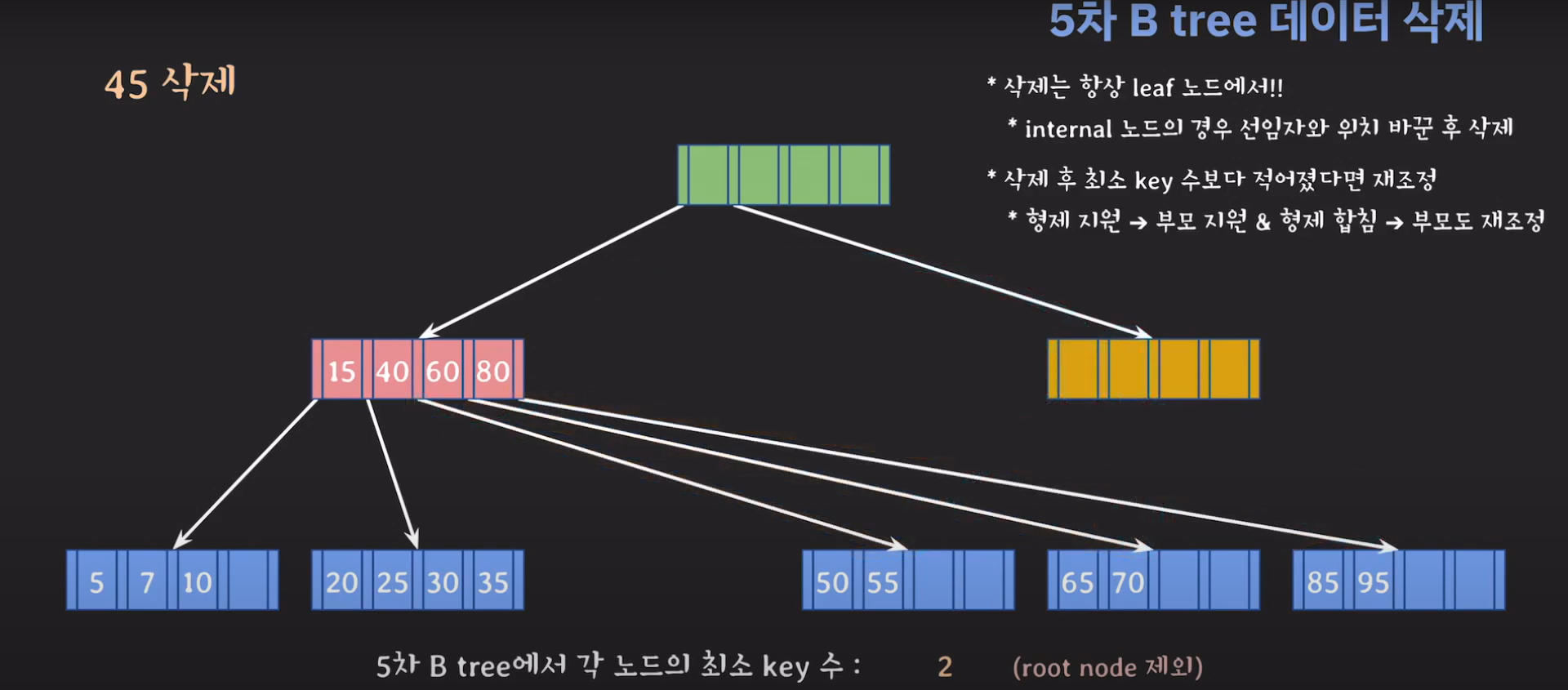
이제 노란색은 비어있으므로 삭제해줍시다.
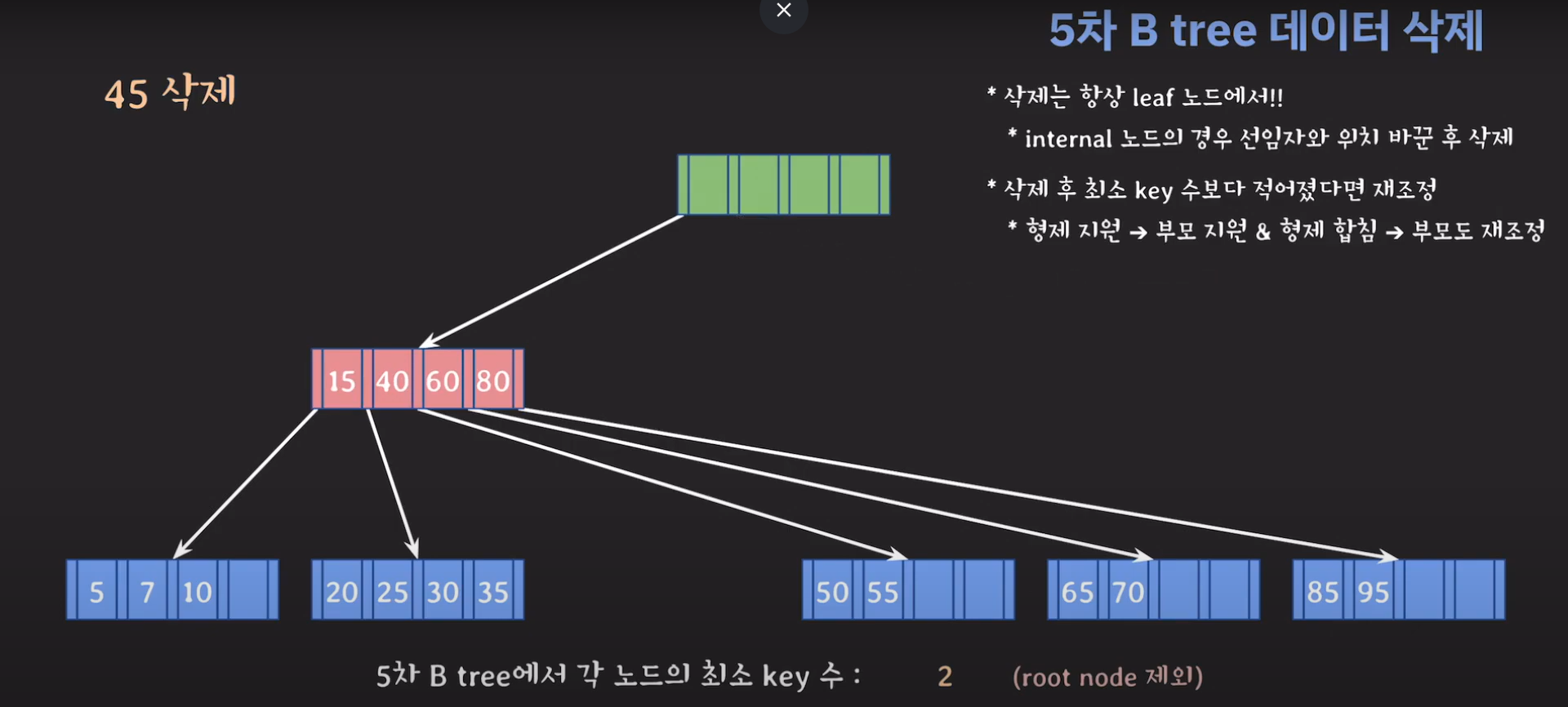
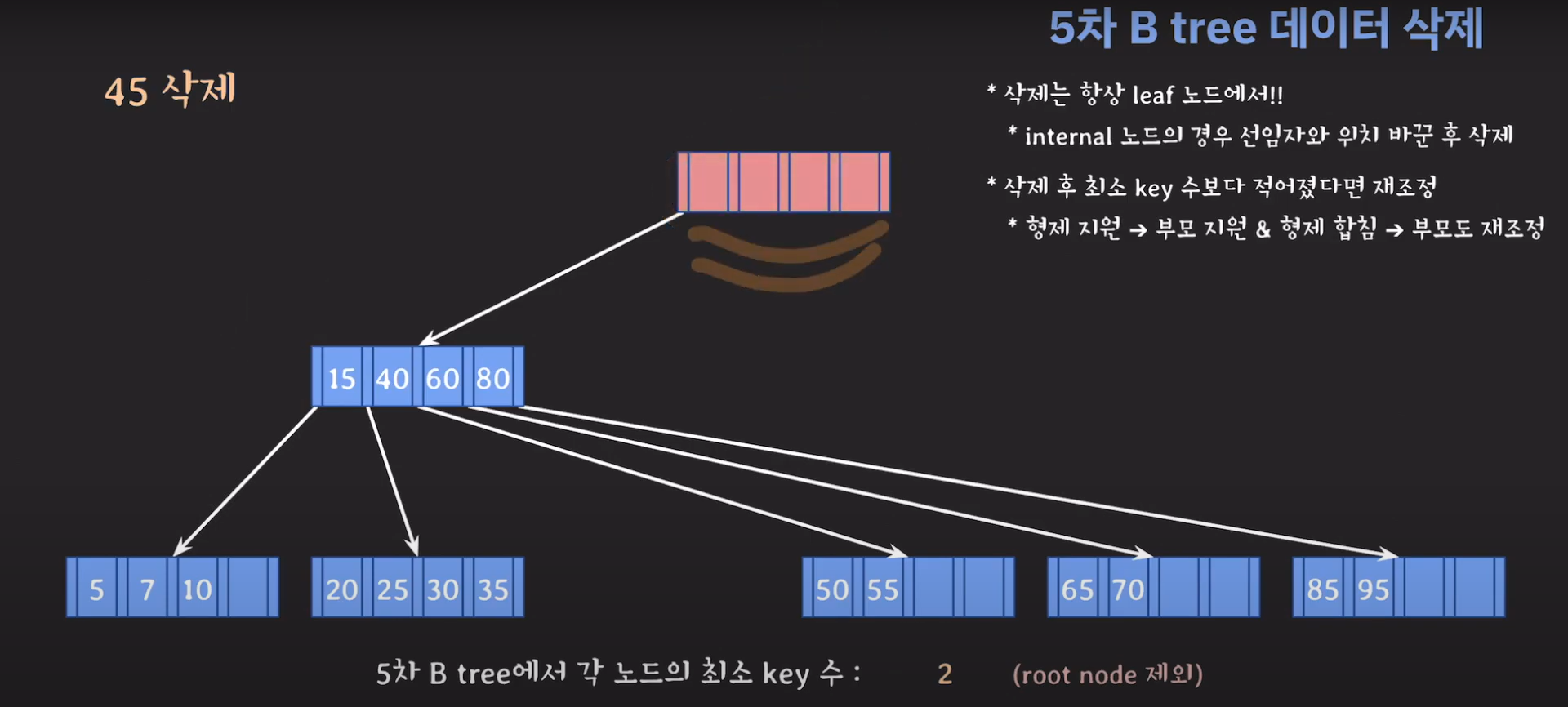
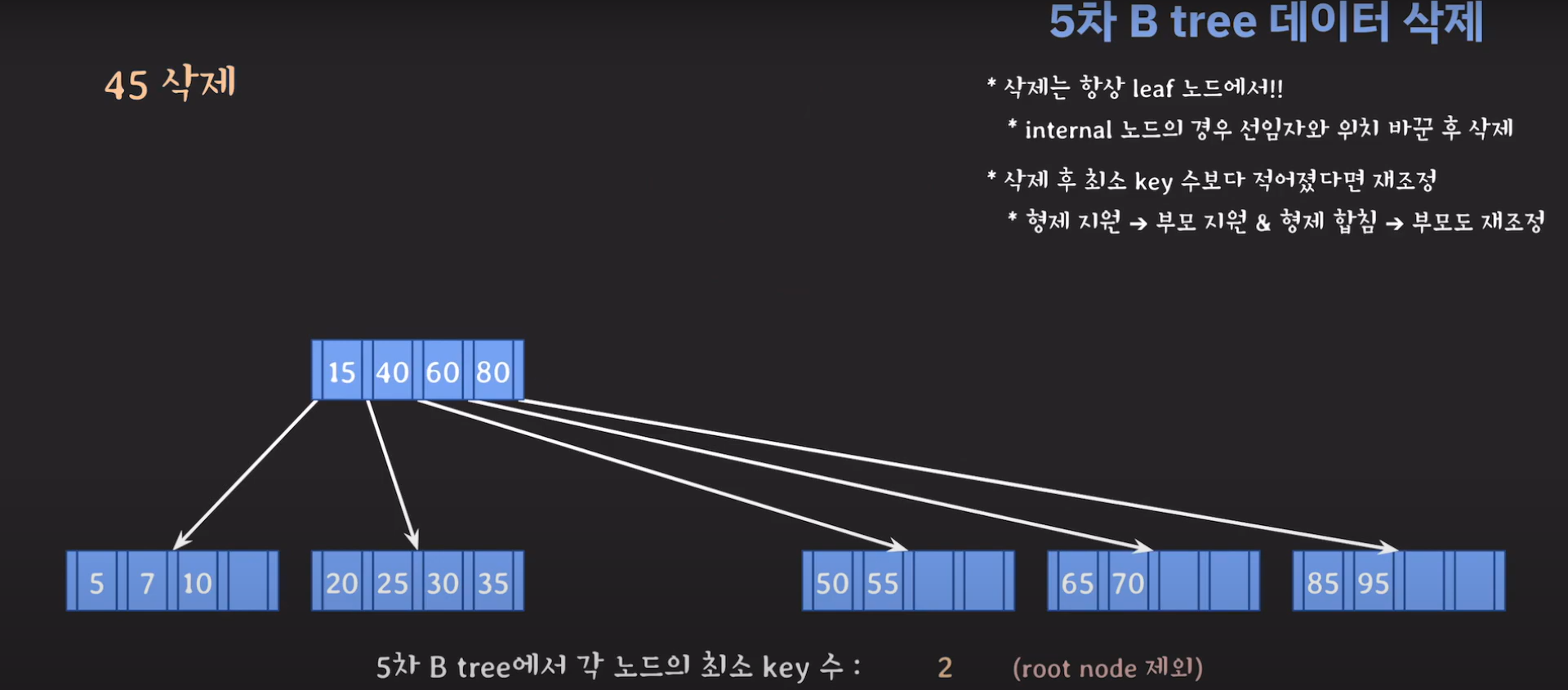
루트 노드가 조건에 맞지 않기 때문에 재배치 해주어야 합니다. 루트노드는 데이터가 없을 경우 삭제해주면 됩니다.
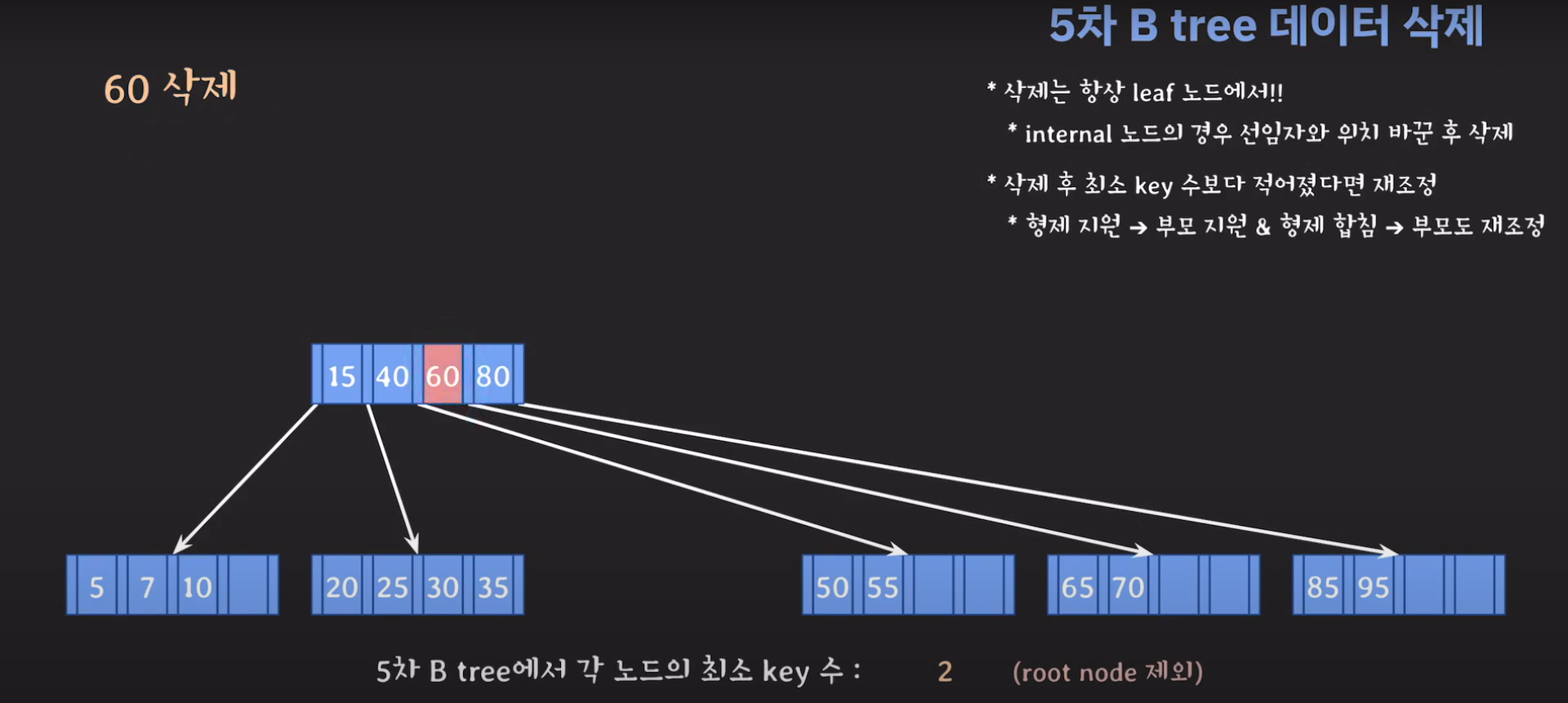
60은 internal 노드이므로 선임자와 바꿔줍시다.
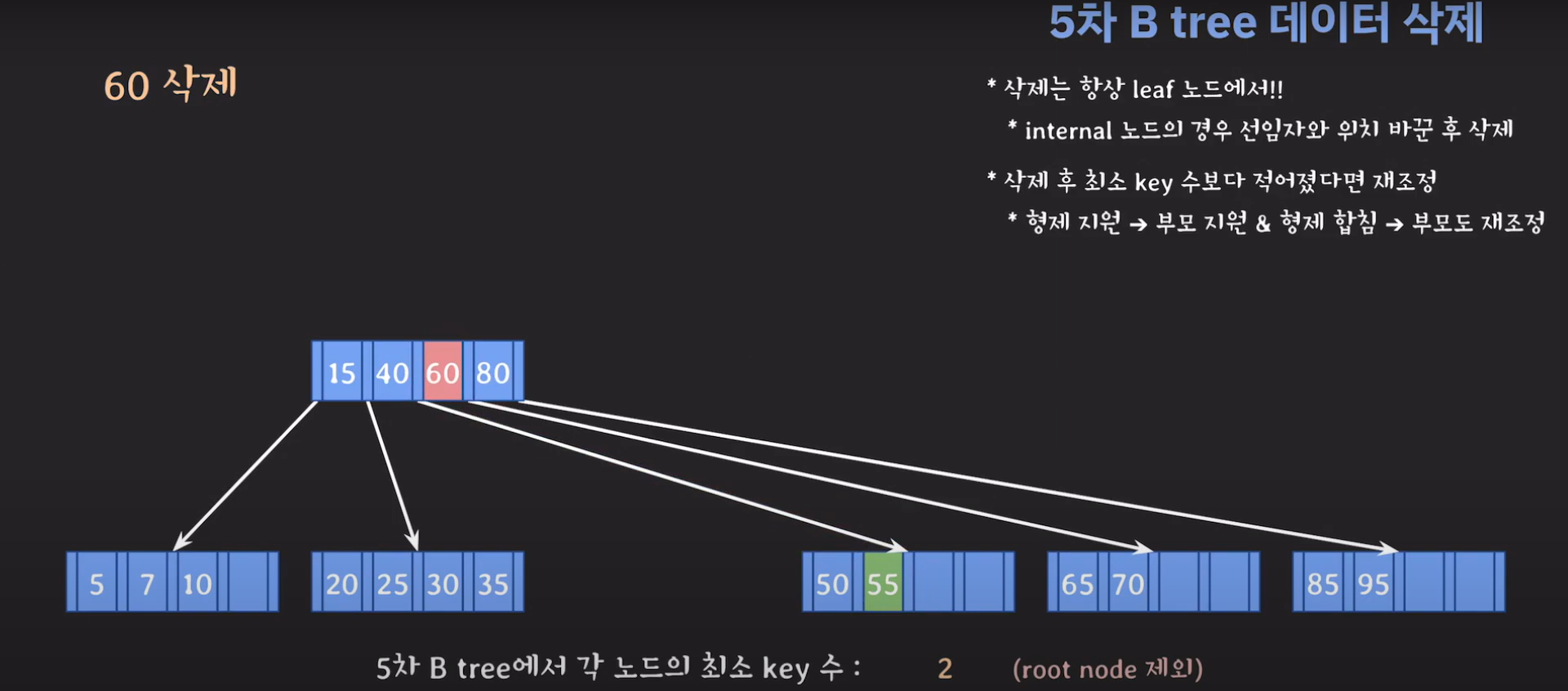
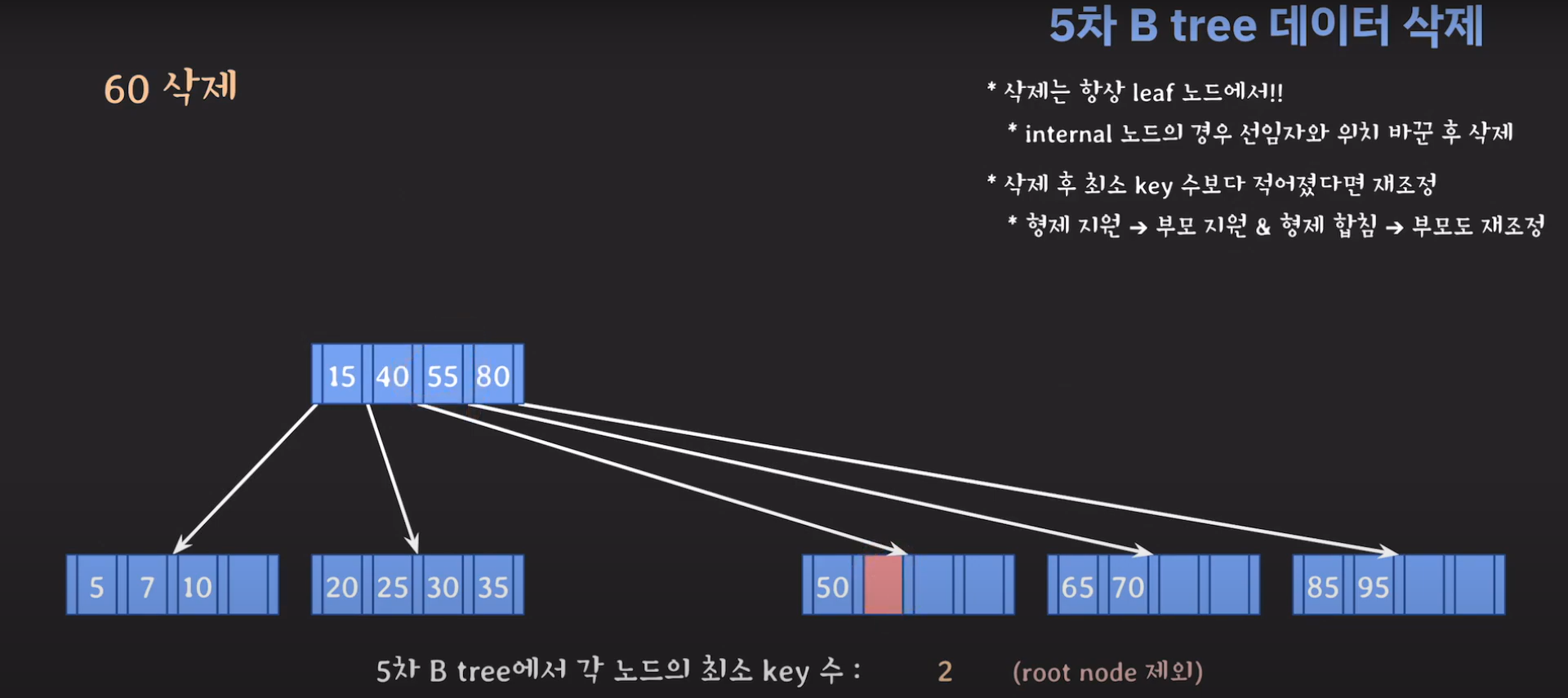
조건이 맞지 않으니 먼저 동생한테 부탁해봅시다.

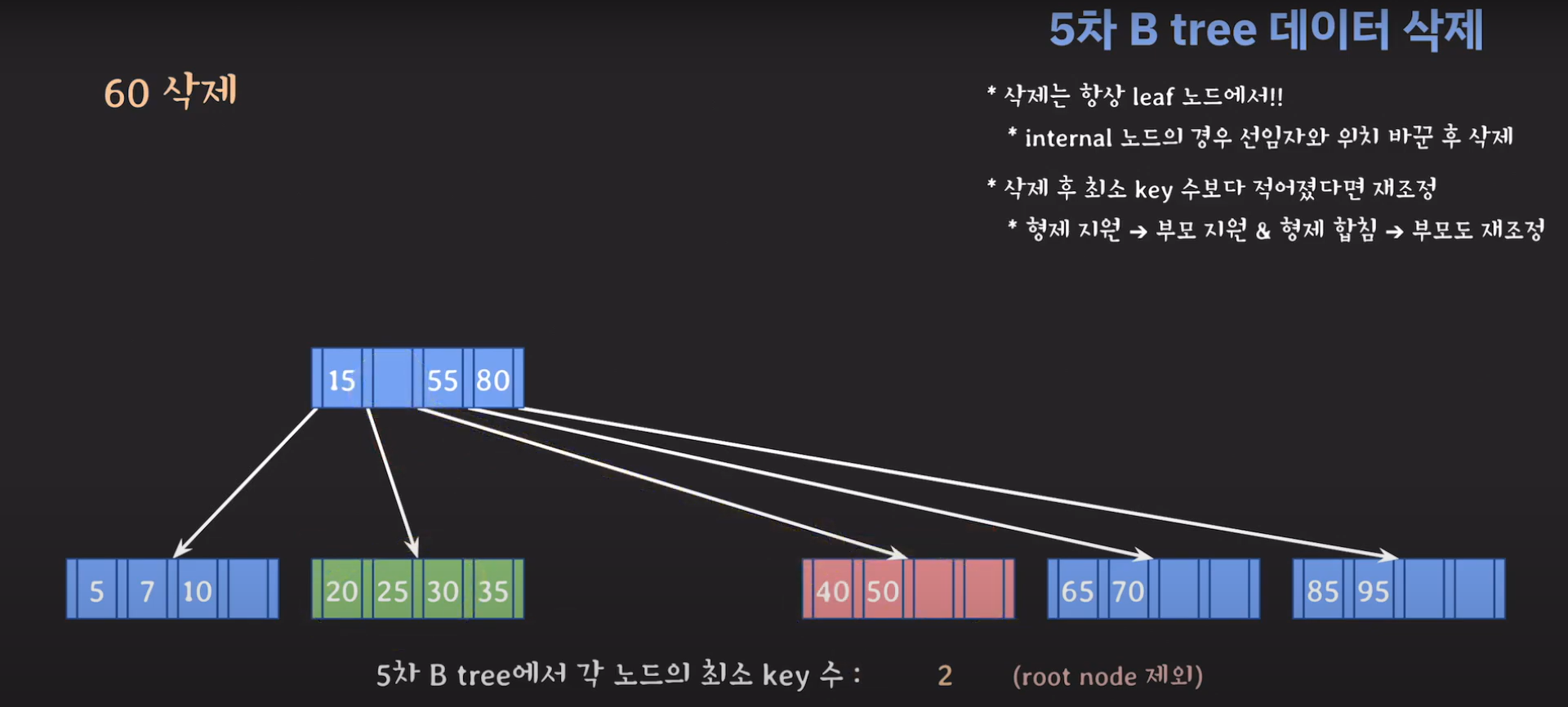
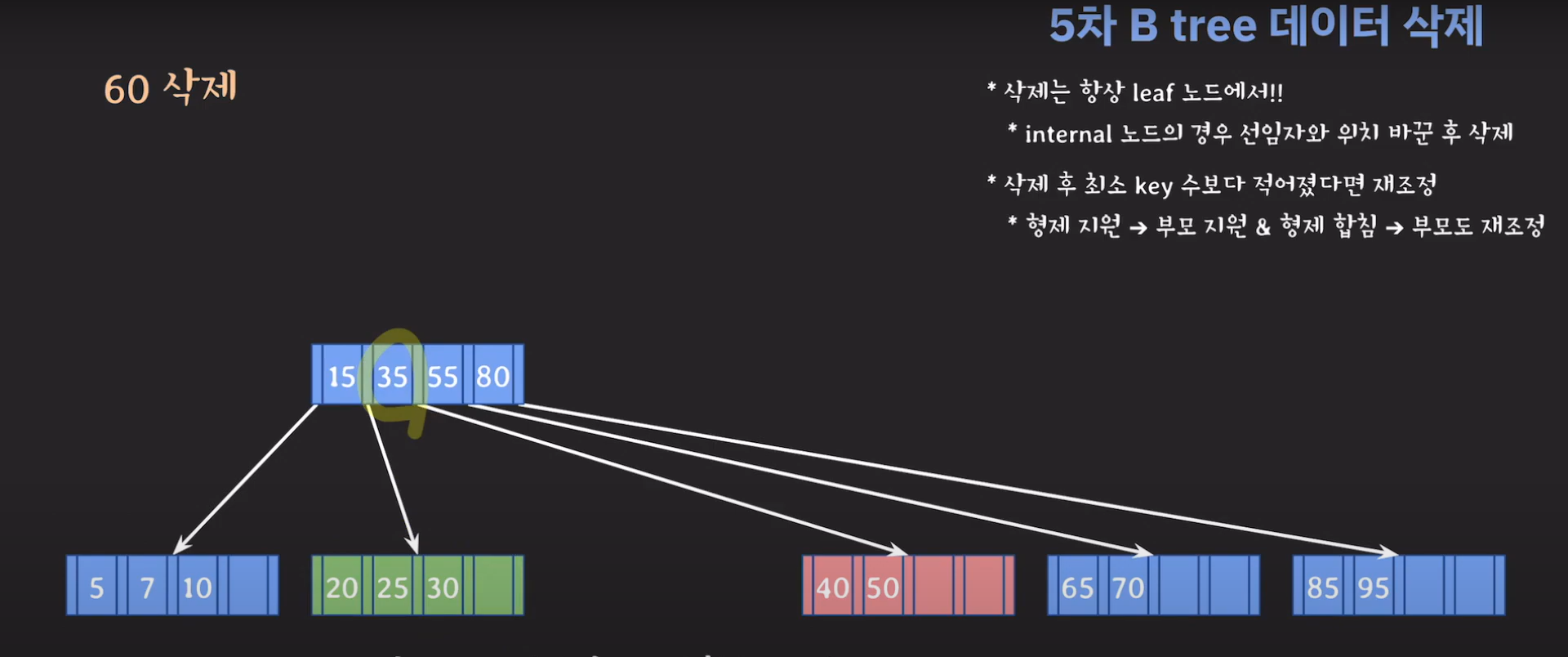
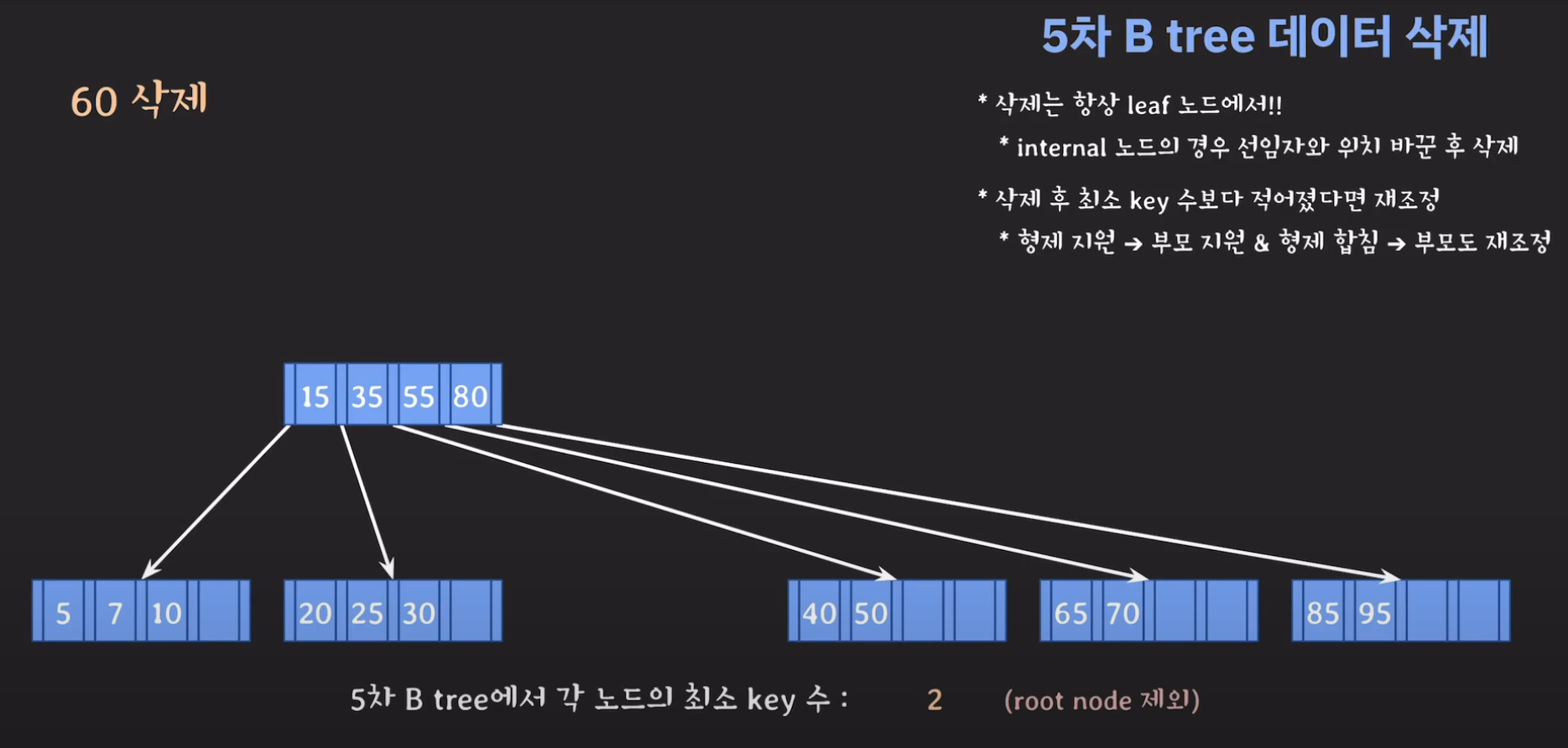
B tree 시간 복잡도

B tree, AVL Tree, Red-Black Tree 모두 시간 복잡도가 O(logN)인데 왜 B tree를 index의 자료구조로 사용하는 것일까요?
이 질문에 답을 하기 위해서는 먼저 우리가 컴퓨터 시스템에 대해서 다시 한 번 살펴볼 필요가 있습니다.
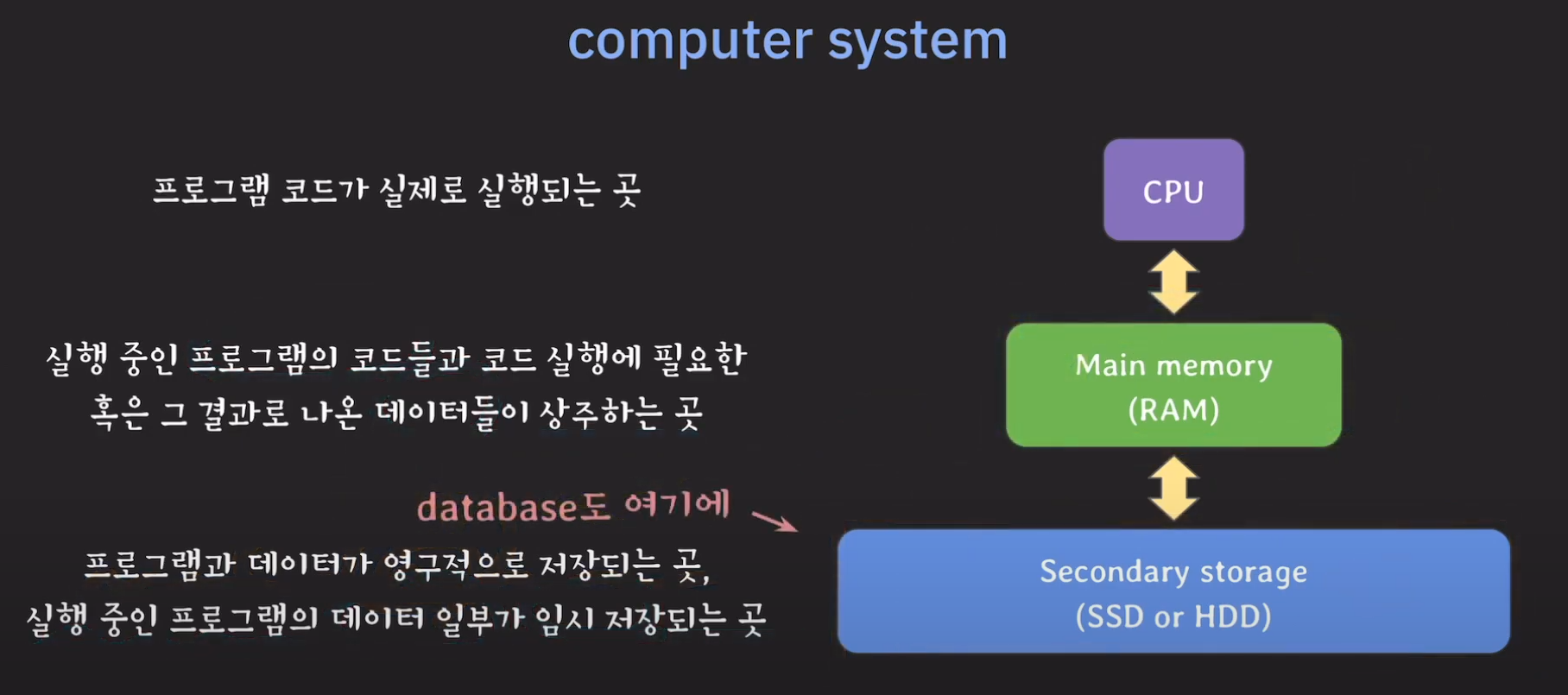
우리는 데이터베이스에 대해 궁금하니 데이터베이스가 일반적으로 어디에 저장되는지 확인해봅시다.
- 실행 중인 프로그램의 데이터 일부가 임시 저장되는 것을 swap이라고 합니다.
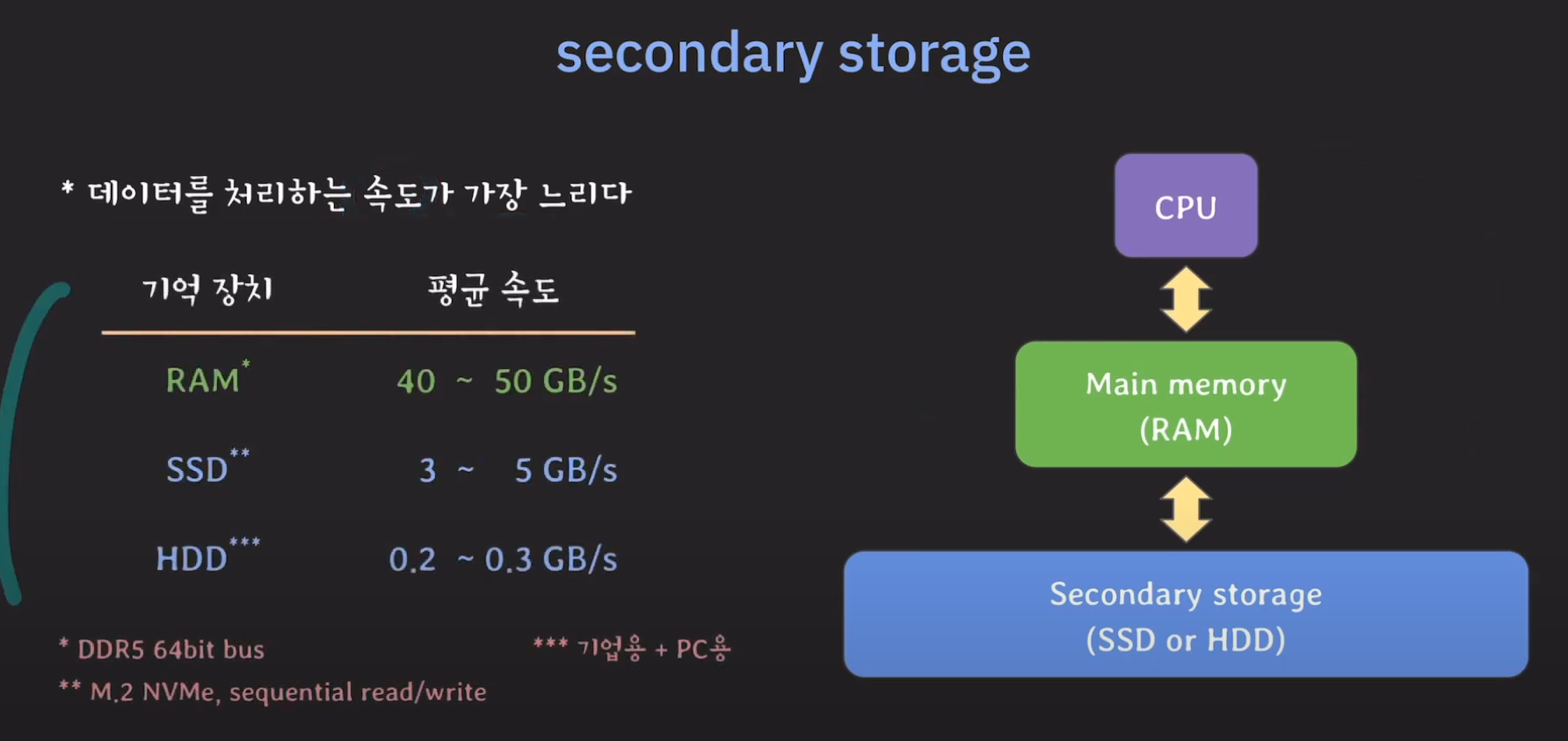
Secondary Storage의 특징을 살펴봅시다.
속도는 다음과 같습니다.
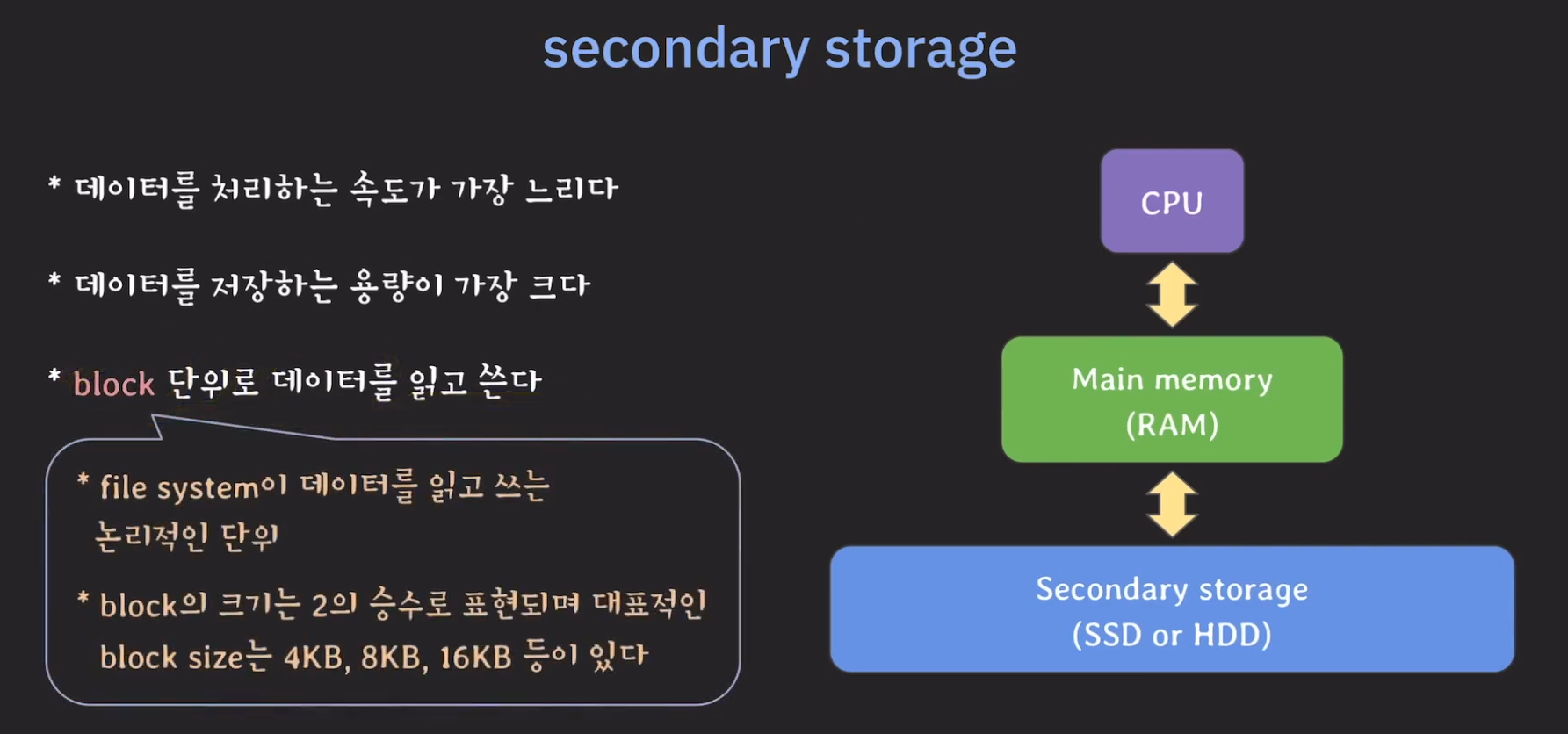
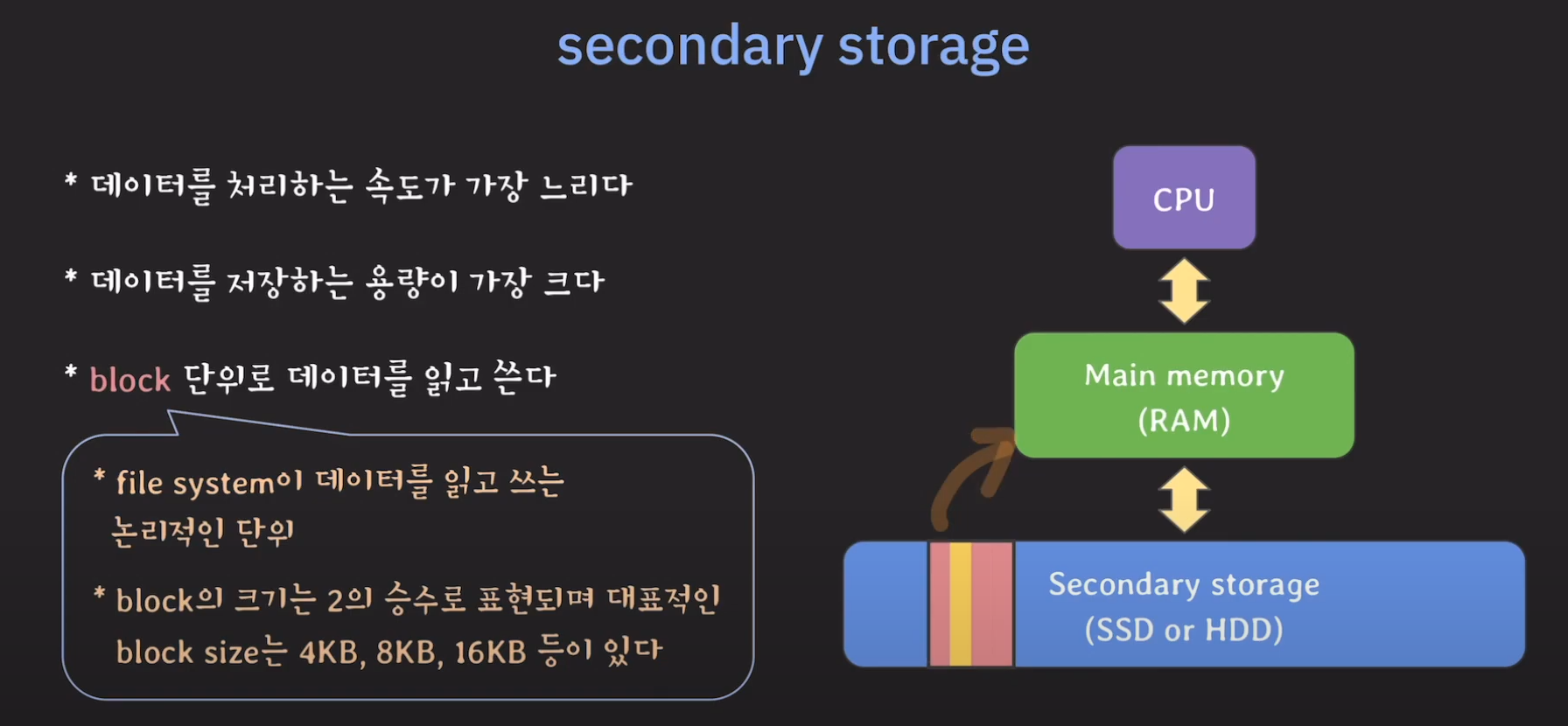
만약 원하는 데이터를 가져오고 싶다면 해당 데이터만 메모리로 올릴 수 없고 block 단위로 메모리에 올려야 합니다.
이렇게 처리하는 경우 장,단점이 존재하게 됩니다.
단점은 불필요한 데이터까지 읽어올 가능성이 있습니다. 반면에 장점은 block에 추후에 필요한 데이터가 있을 경우 성능을 높일 수 있습니다.
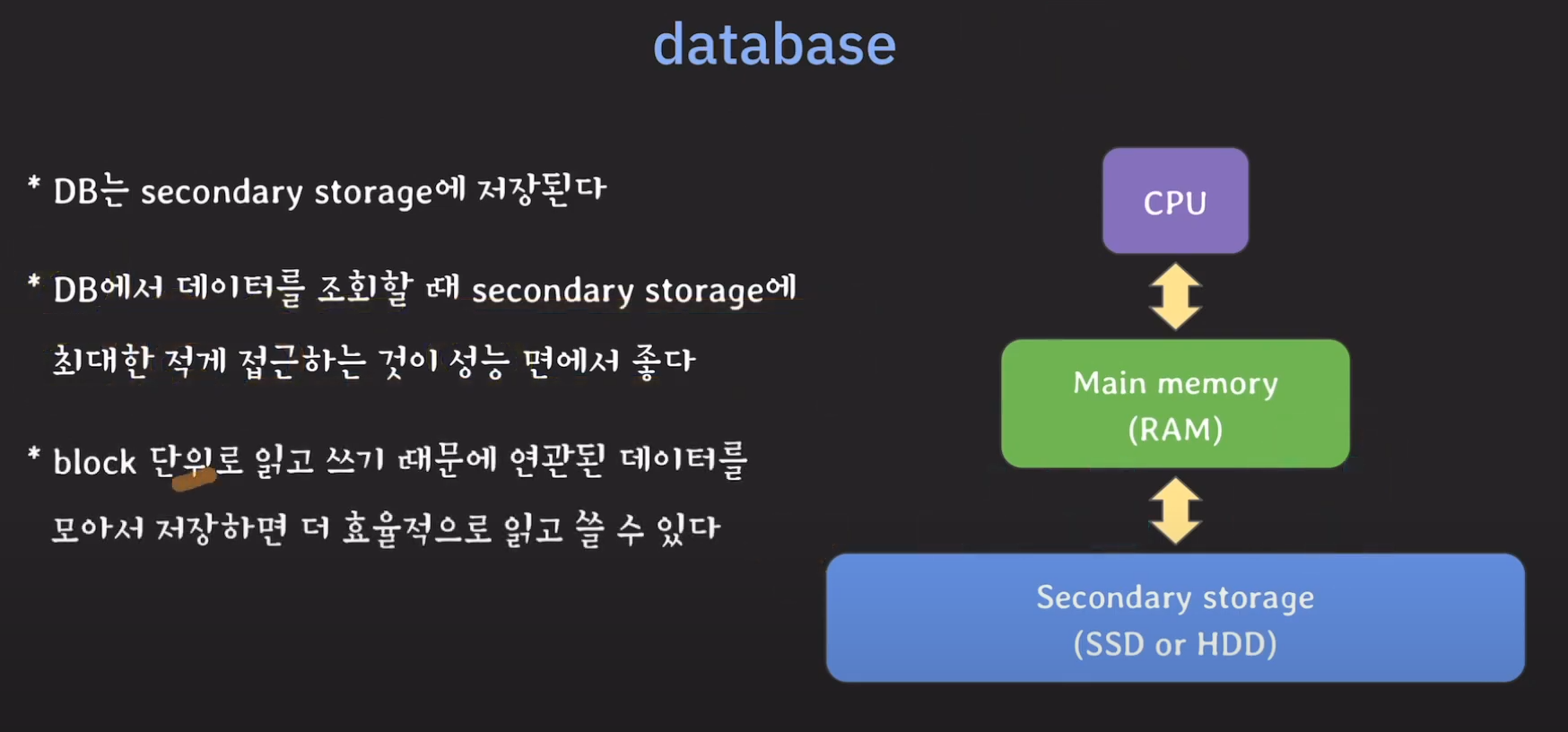
Secondary Storage는 영구적으로 데이터를 저장하기 때문에 데이터베이스는 Secondary Storage에 저장하는것이 논리적으로 알맞습니다.

AVL Tree와 B tree를 비교하면 B Tree를 인덱스의 자료구조로 선택했는지 더 잘 이해할 수 있기 때문에 비교해 봅시다.
추가적으로 위 내용을 가정하고 비교해 봅시다.
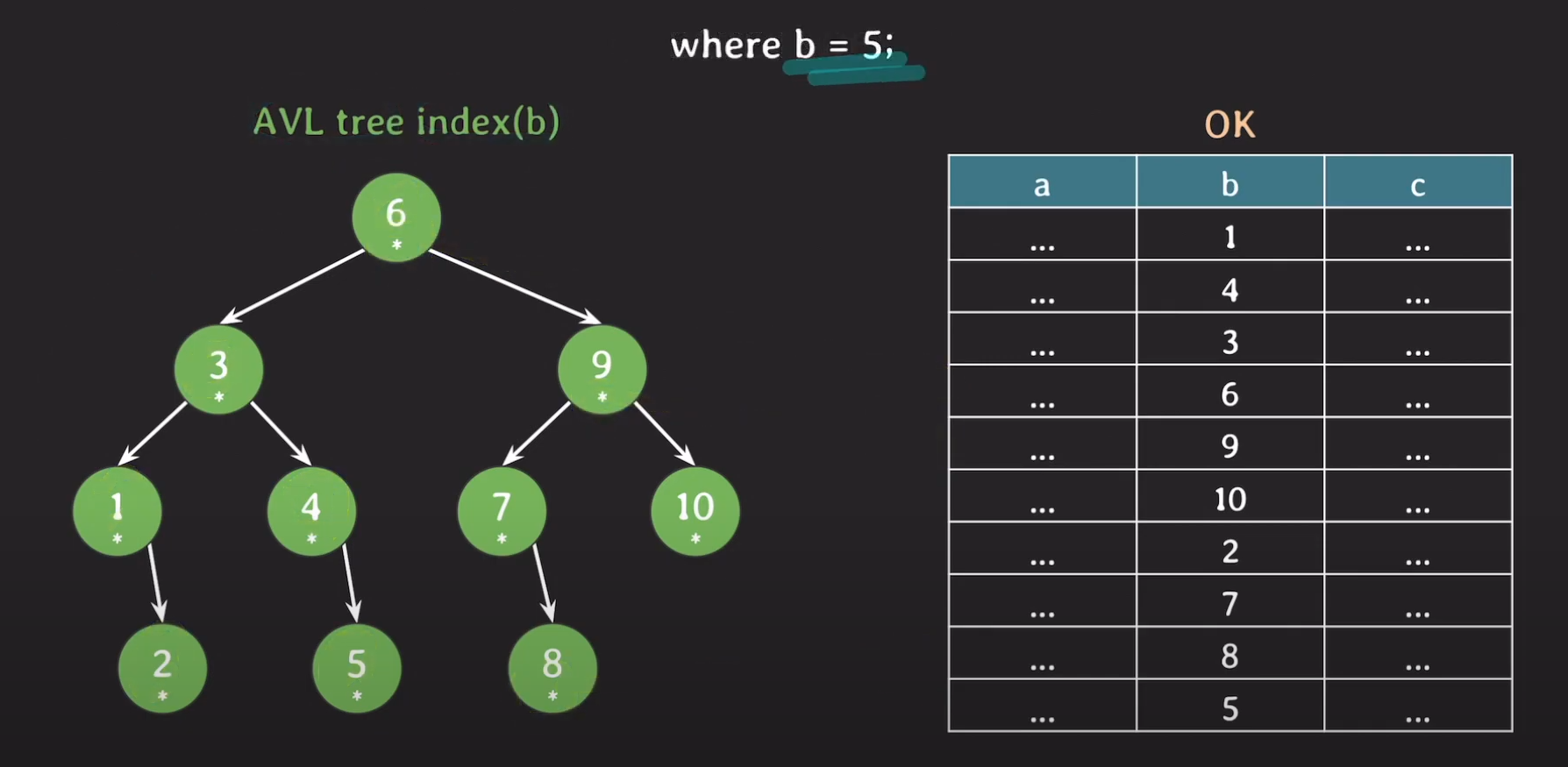
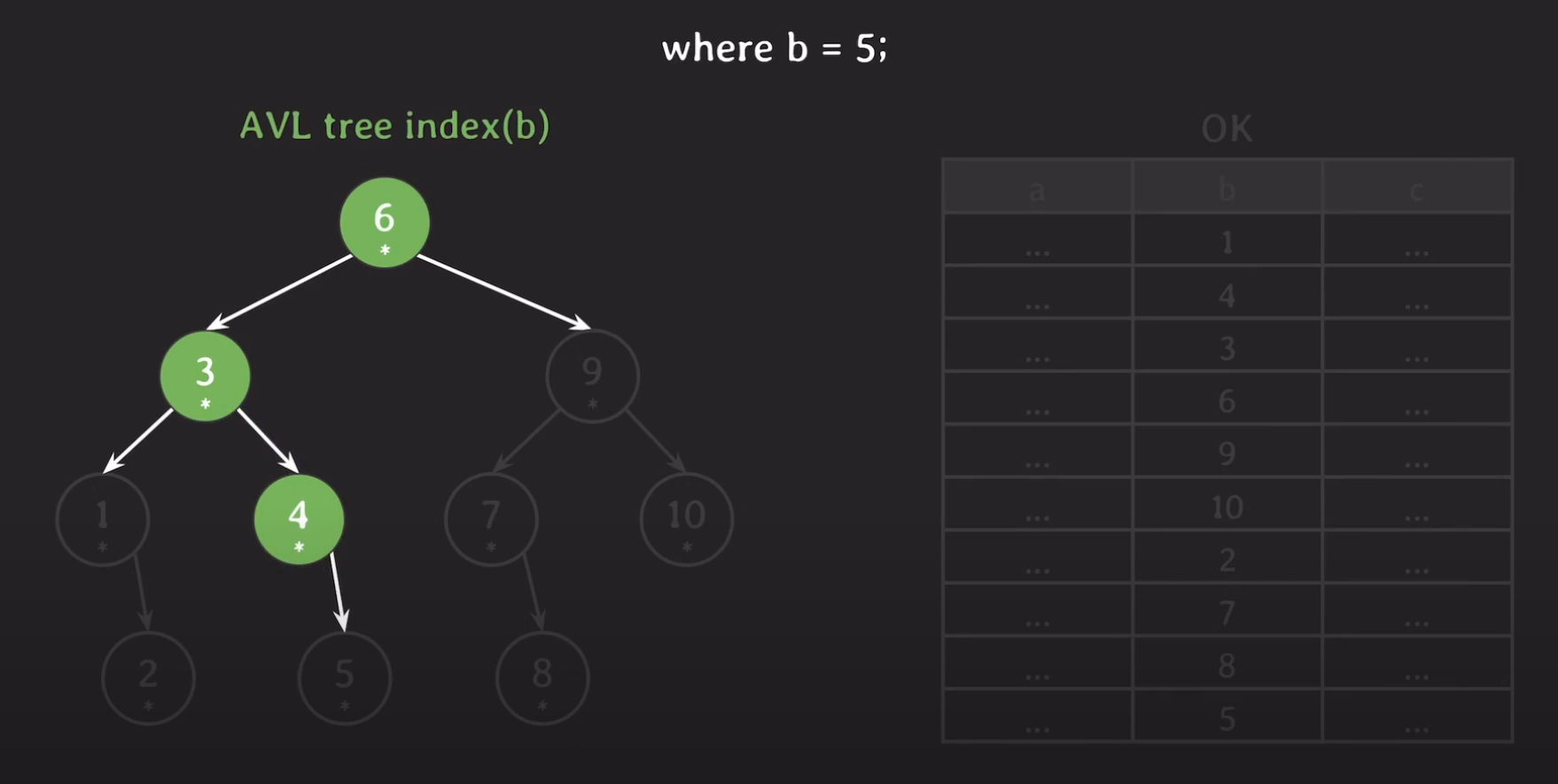
데이터를 AVL Tree로 표현하면 위와 같습니다. 이제 5라는 데이터롤 요청했다고 해봅시다.
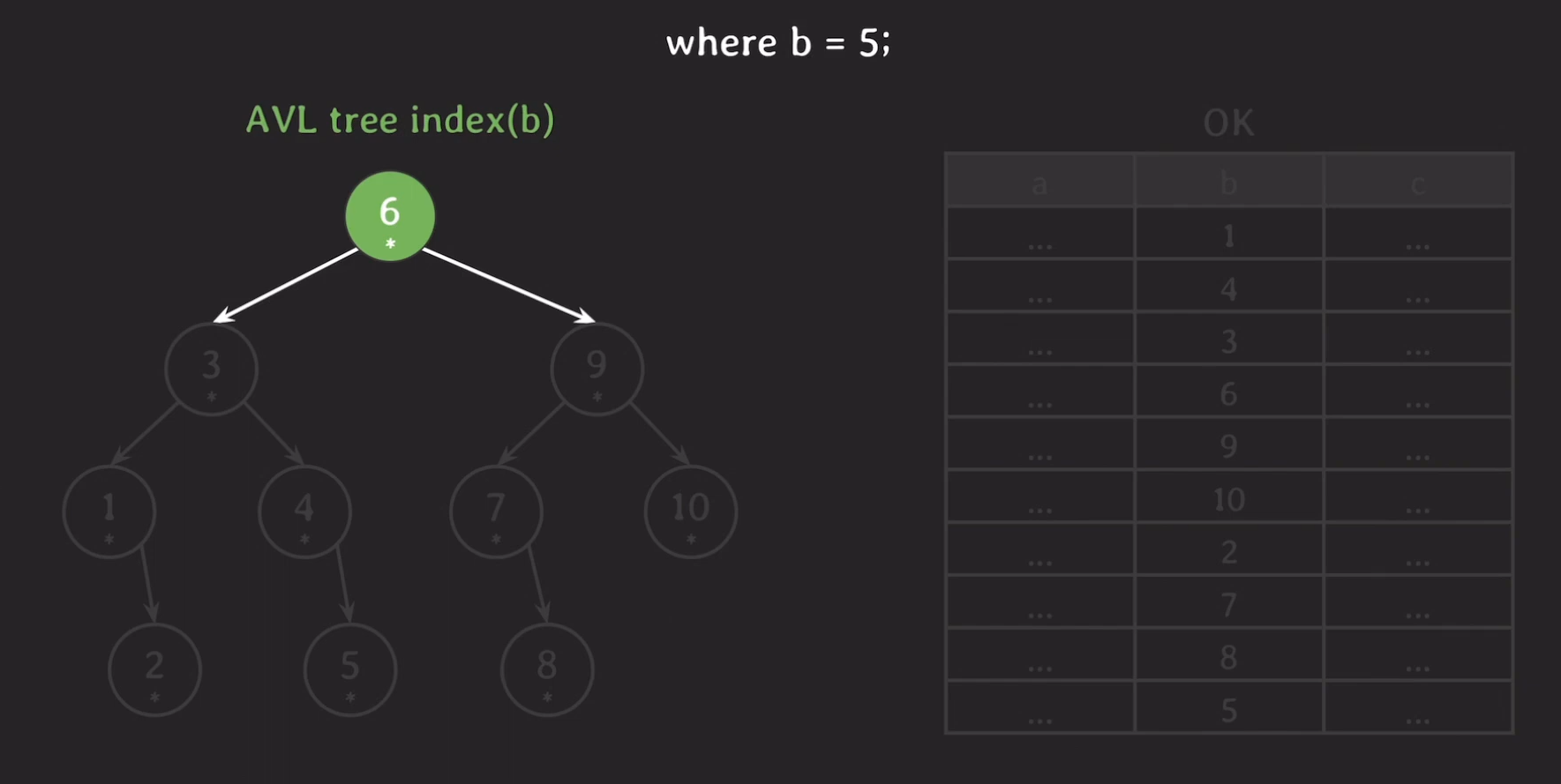
가정에 의해 현재 메모리에 올라와 있는 데이터는 루트 노드 뿐이며 다르 노드들은 아직 Secondary Storage에 있으므로 음영 처리를 해줬습니다.
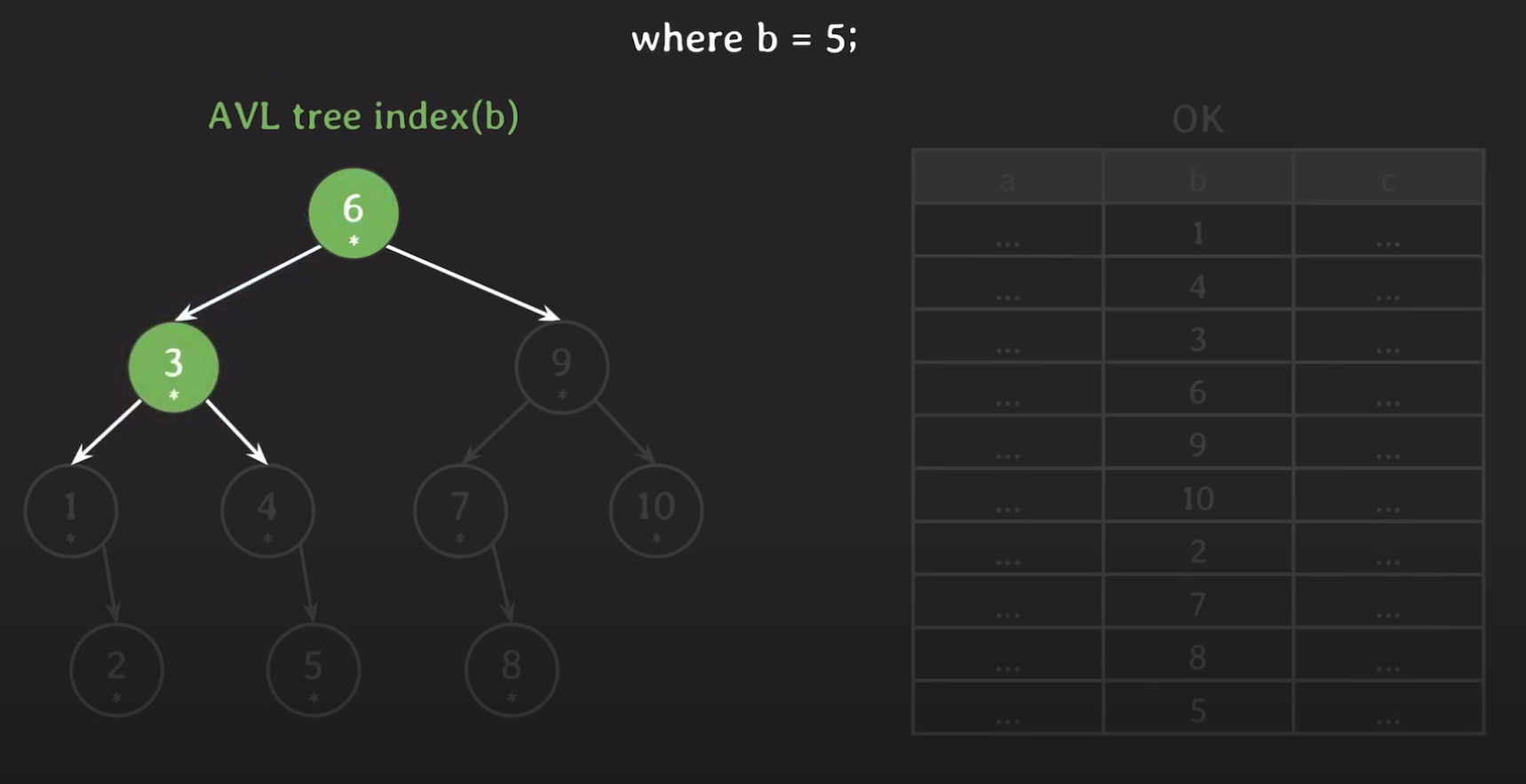
5는 6보다 작기 때문에 왼쪽으로 가고 왼쪽 자식 노드는 현재 메모리에 없기 때문에 Secondary Storage에서 데이터를 읽어와 메인 메모리에 올립니다.
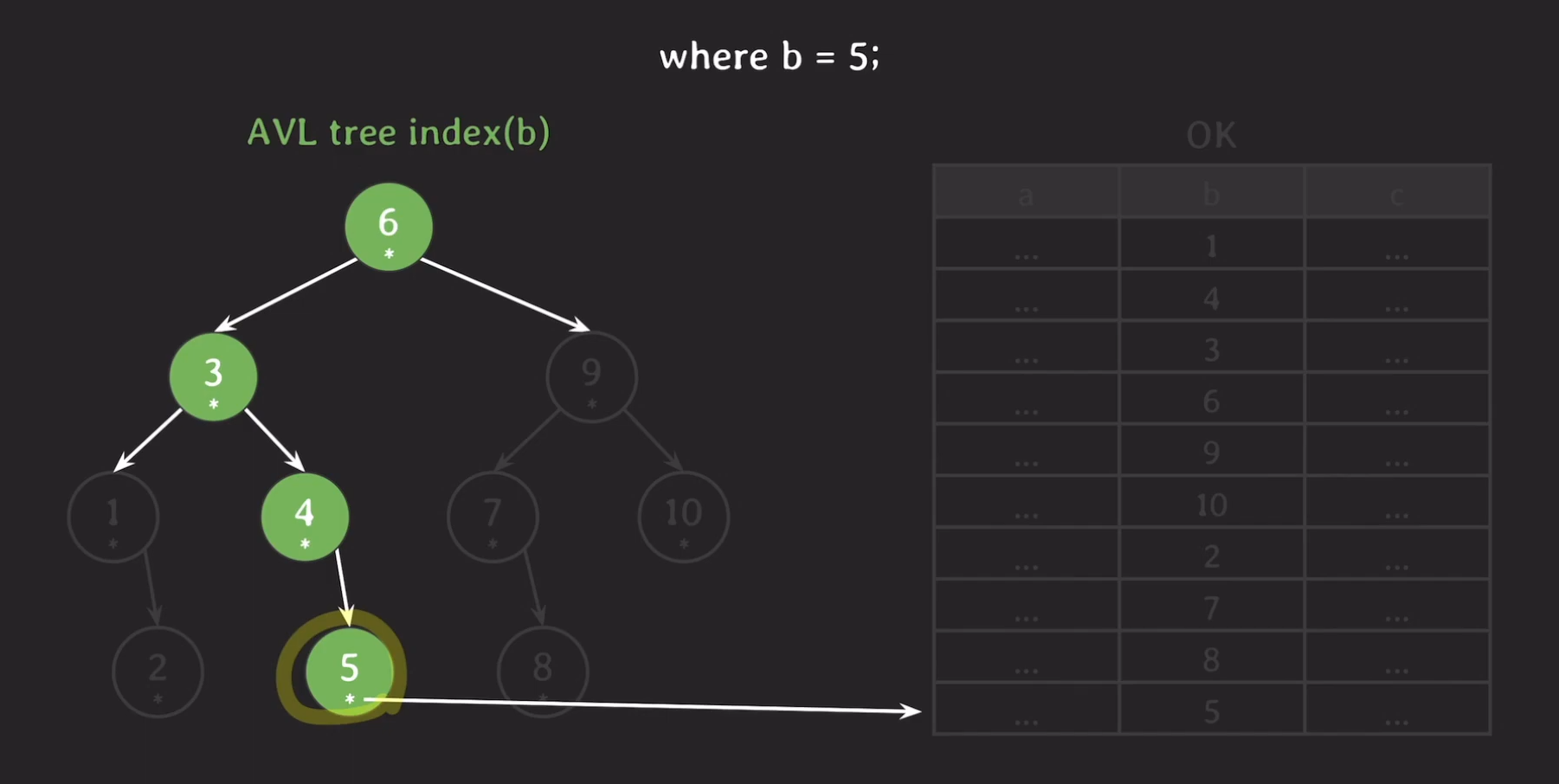
마지막으로 5가 실제로 가리키고 있는 데이터들 모두 Secondary Storage에서 읽어와야 합니다.
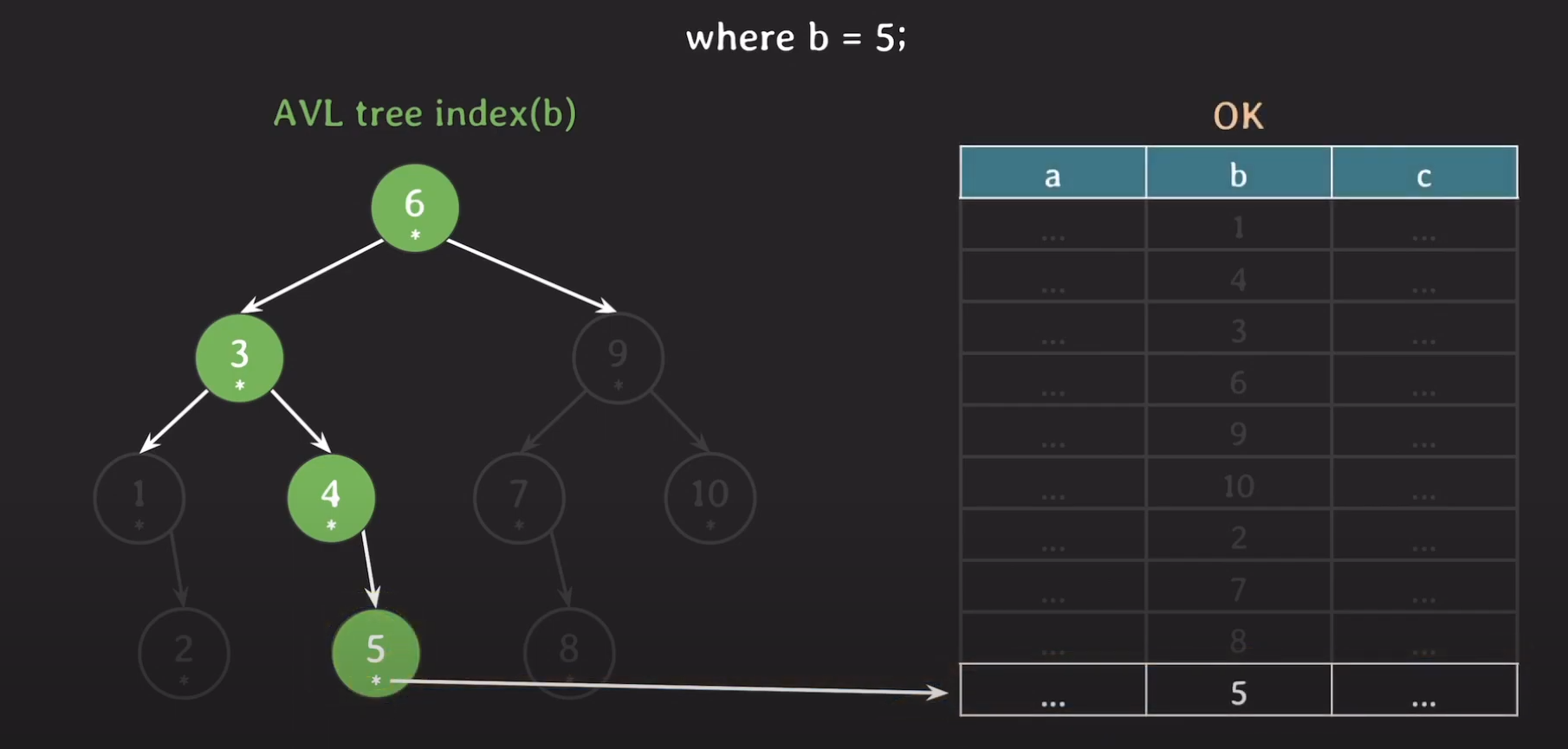
데이터를 메모리로 읽어왔으면 가공해서 반환하게 됩니다.
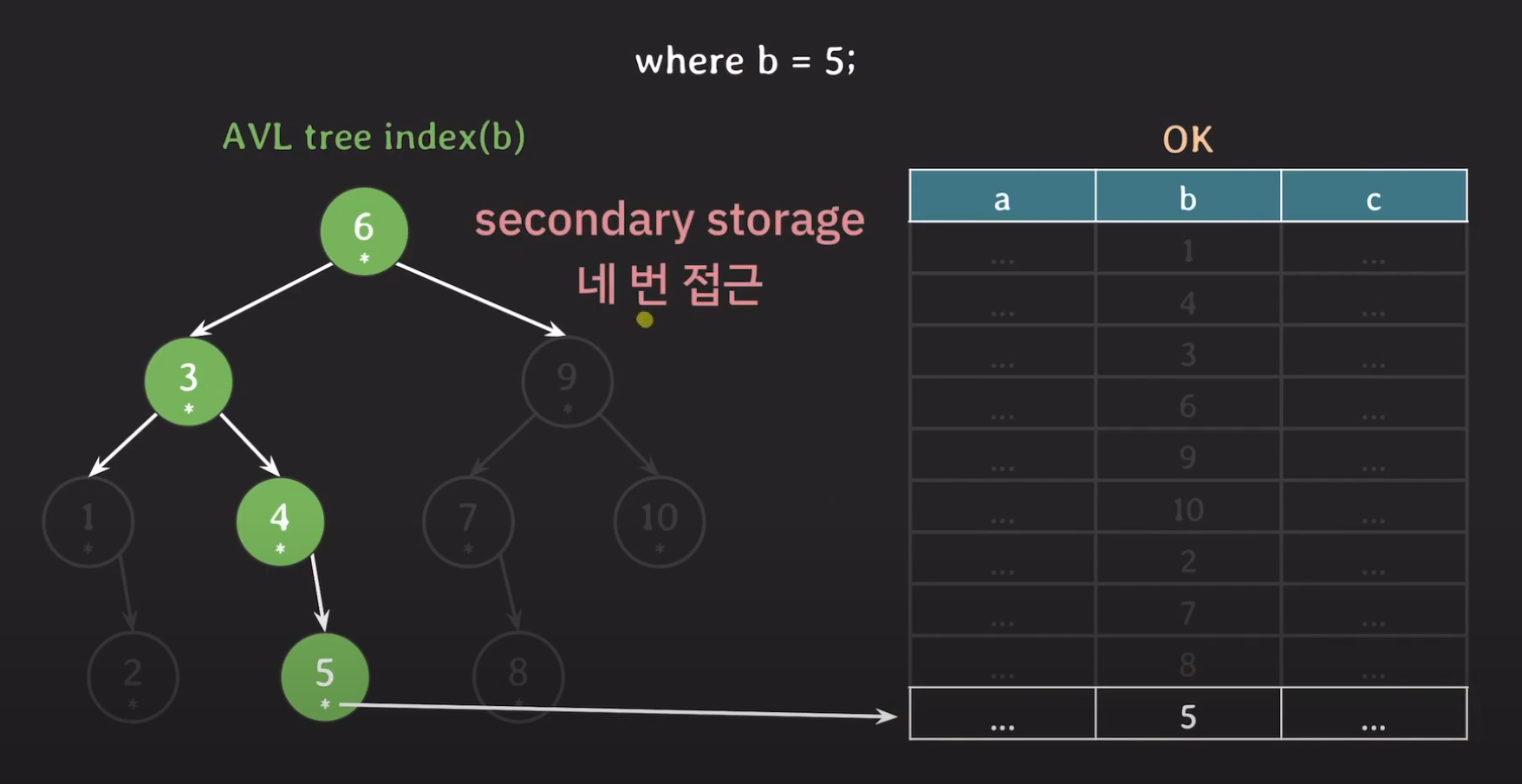
최종적으로 AVL Tree 기반의 Index는 Secondary Storage를 총 4번 접근하였습니다.
이번에는 B tree 기반의 Index를 만들었을 때 어떻게 되는지 살펴봅시다.
이 예제에서는 5차 B tree로 만들어서 비교해 봅시다.
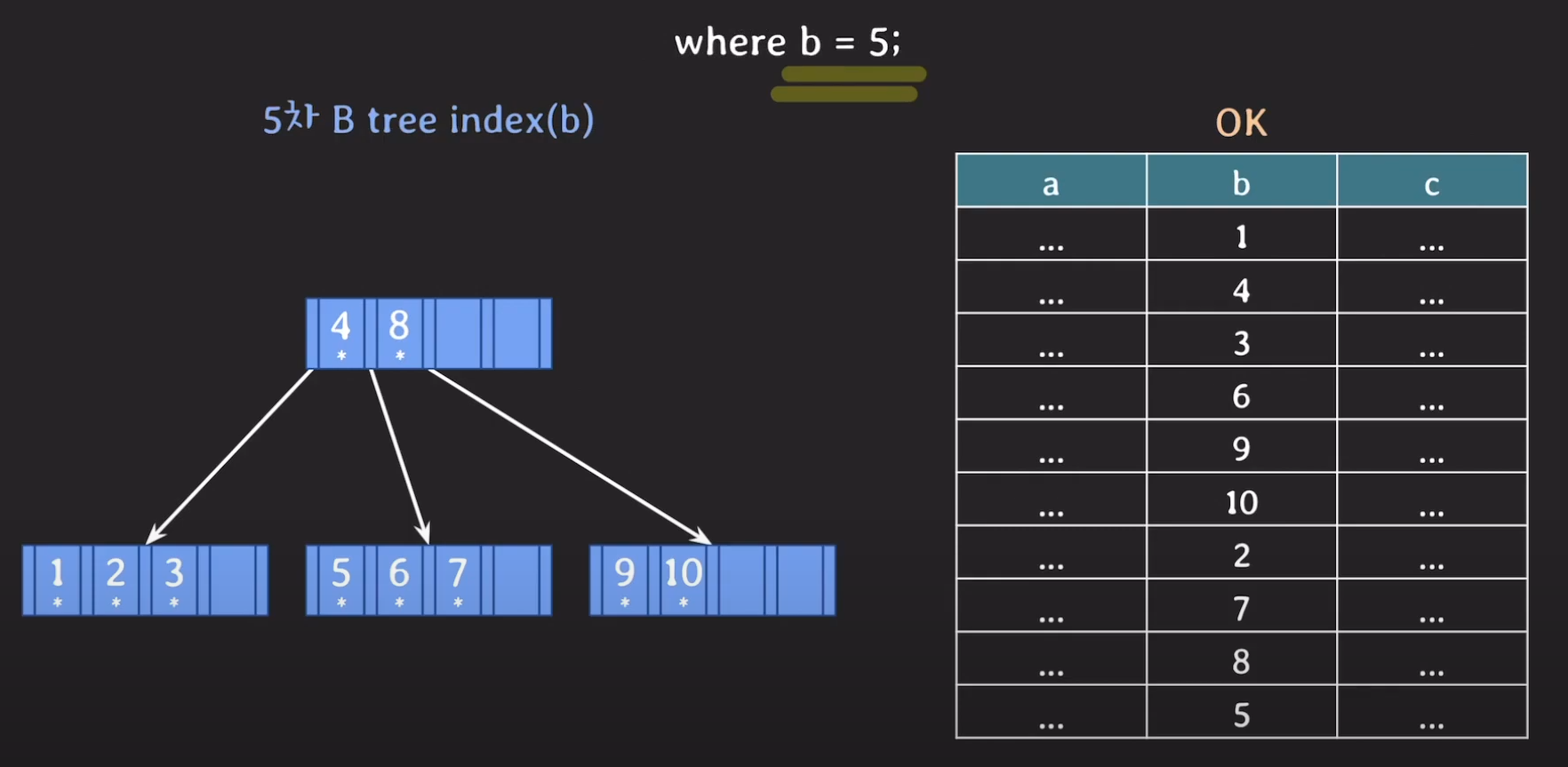
데이터 테이블을 기반으로 인덱스를 만들경우 위와 같이 Tree를 구성할 수 있습니다.
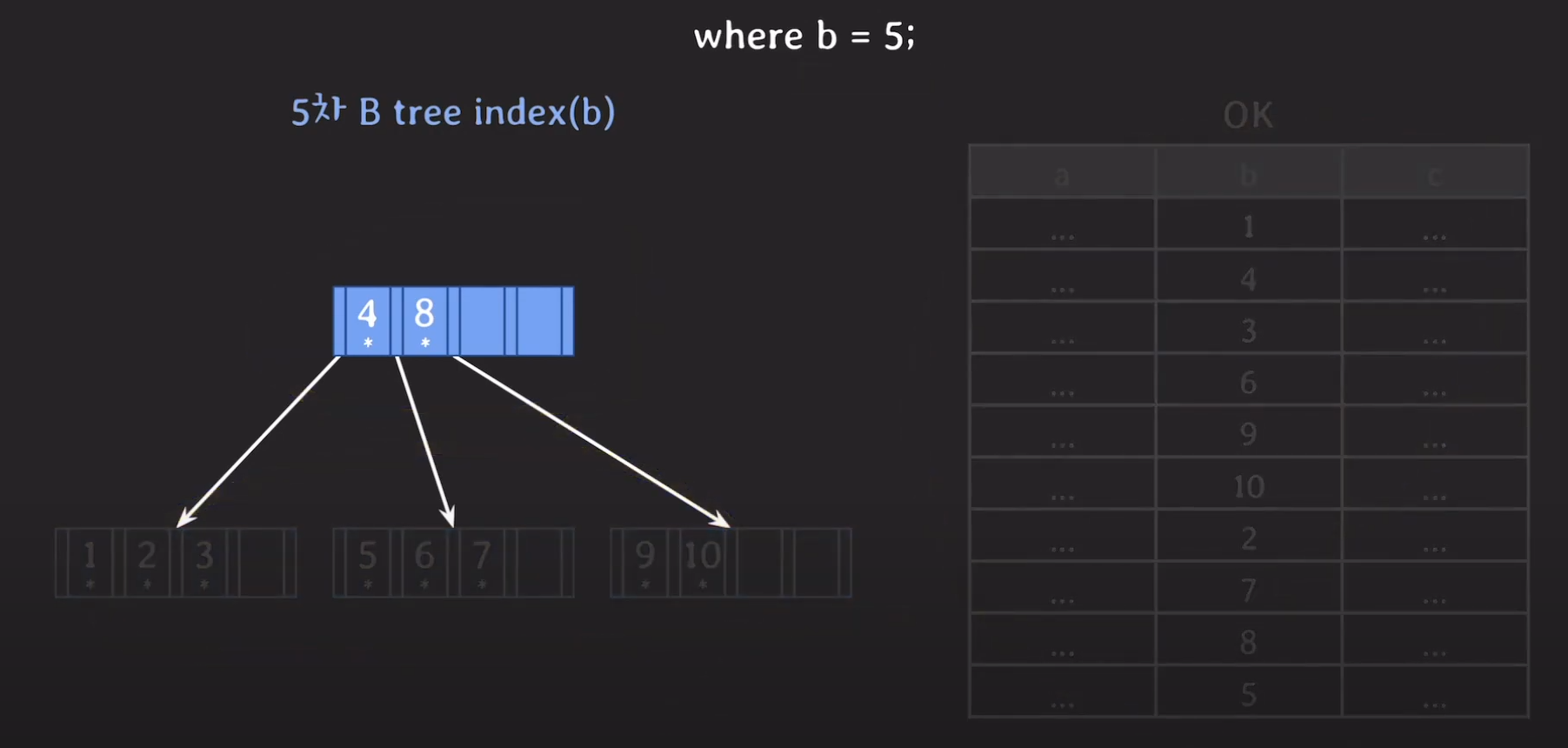
이 역시 루트 노드만 메인 메모리에 올라와 있고 다른 데이터들은 Secondary Storage에 저장되어 있다고 가정합시다.
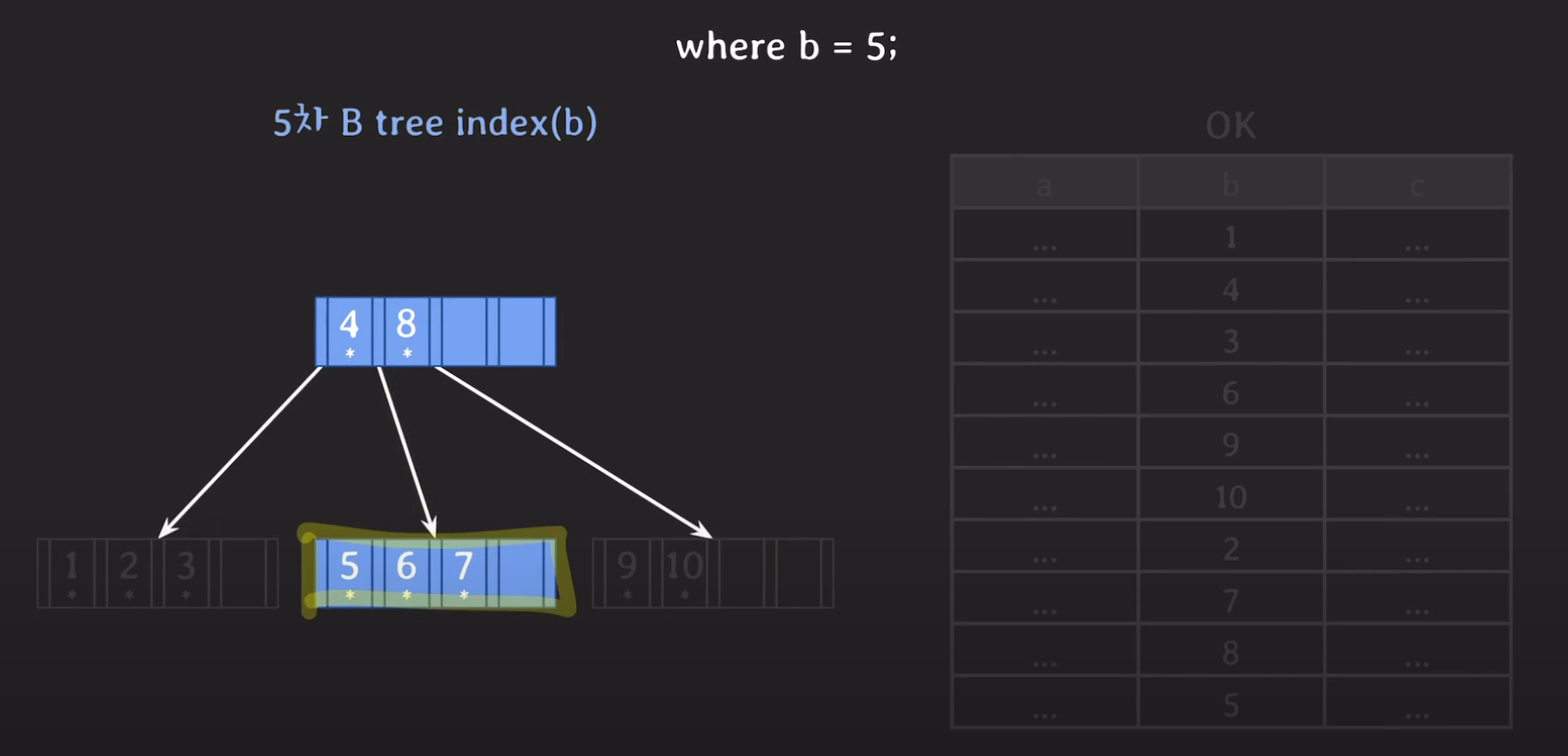
5는 4와 8 사이의 값이므로 중간에 있는 서브트리로 가고 Secondary Storage로 부터 데이터를 읽어옵니다.
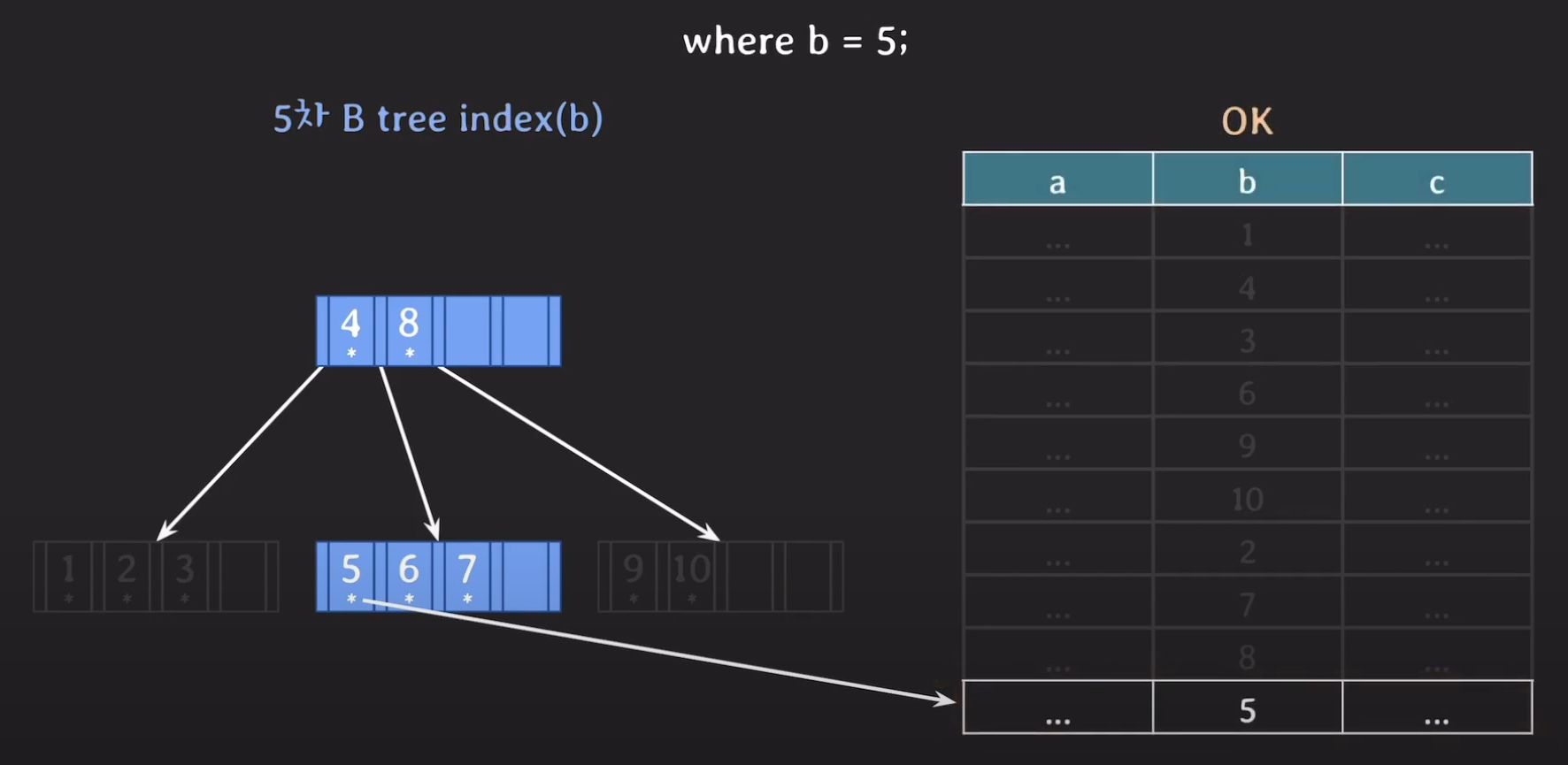
인덱스 5에 해당하는 데이터가 없으므로 Secondary Storage로 부터 데이터를 읽어오게 됩니다.
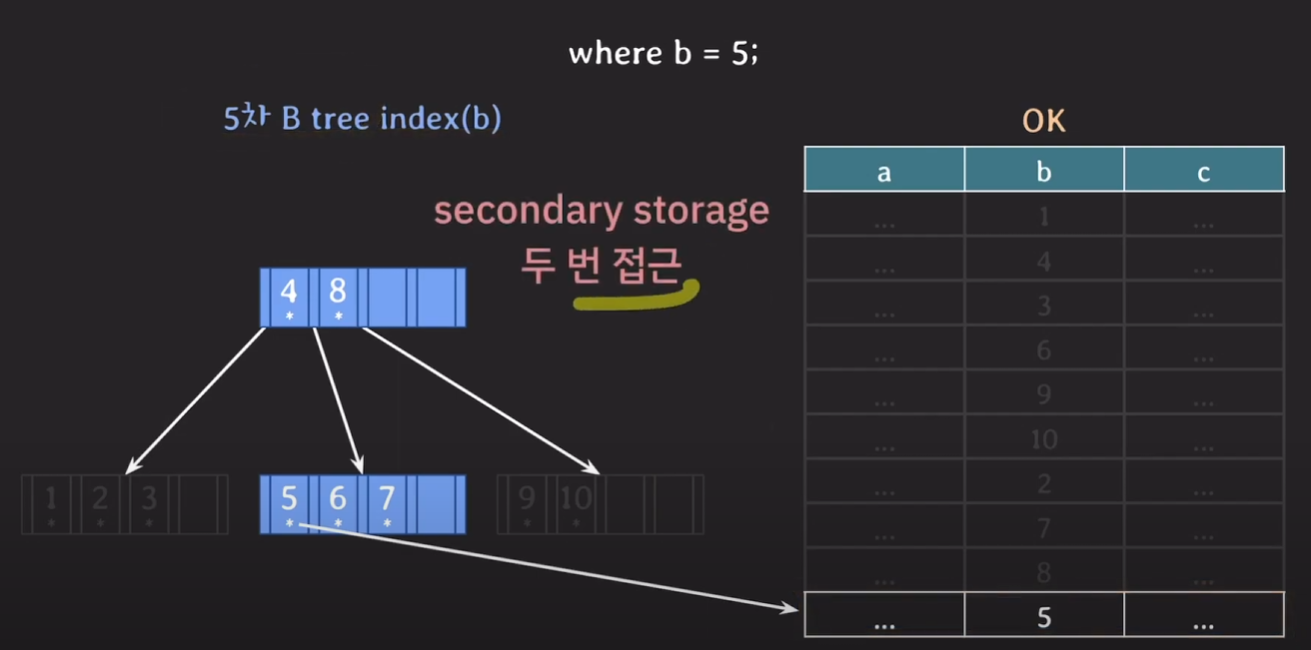
B tree 기반 인덱스는 최종적으로 Secondary Storage에 두 번 접근하게 됩니다.
B tree VS AVL Tree
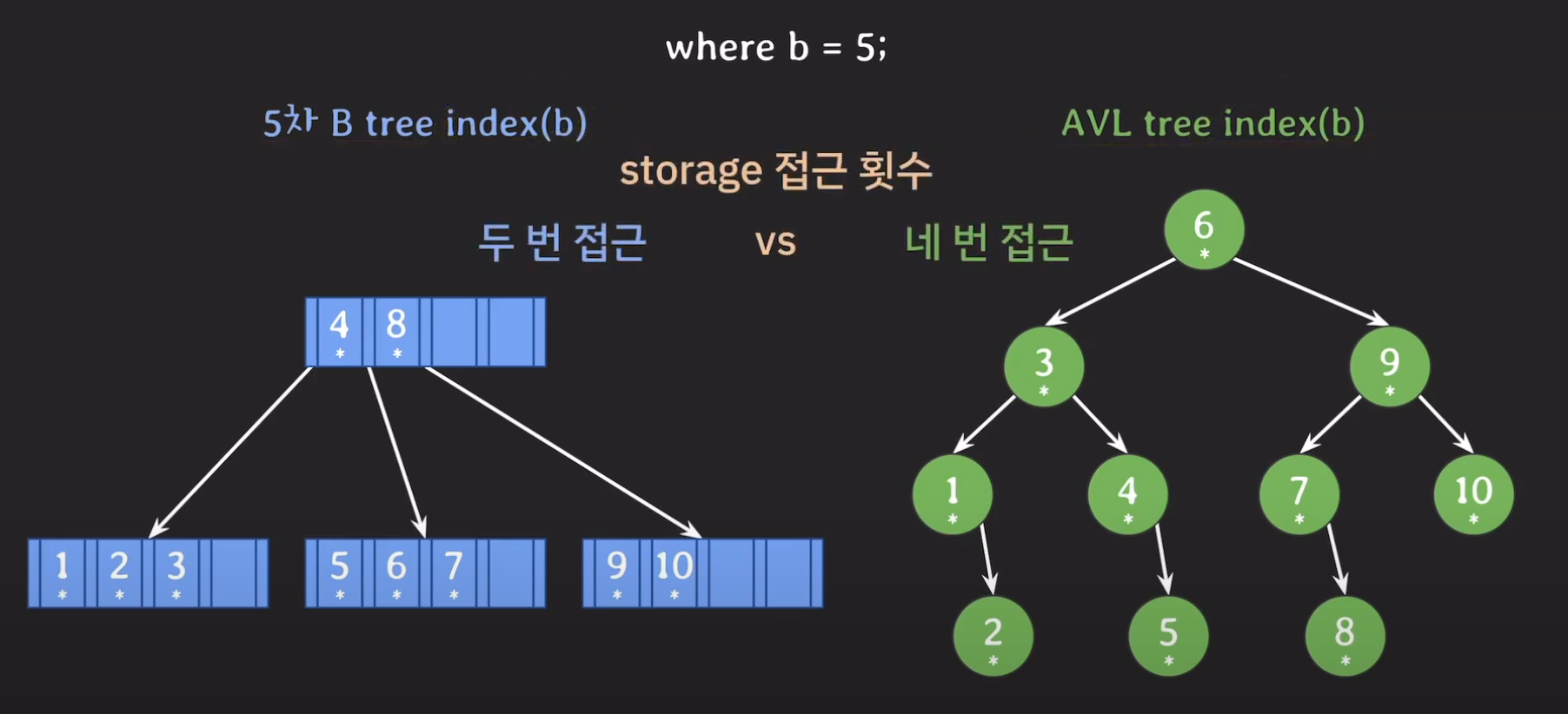
최종 비교를 해보면 B tree 기반의 인덱스가 Secondary Storage에 더 적게 접근하였으므로 속도가 더 빠르다는 것을 알 수 있게 됩니다.
그렇다면 왜 B tree가 더 적은 횟수로 디스크에 접근 할 수 있었을까요?
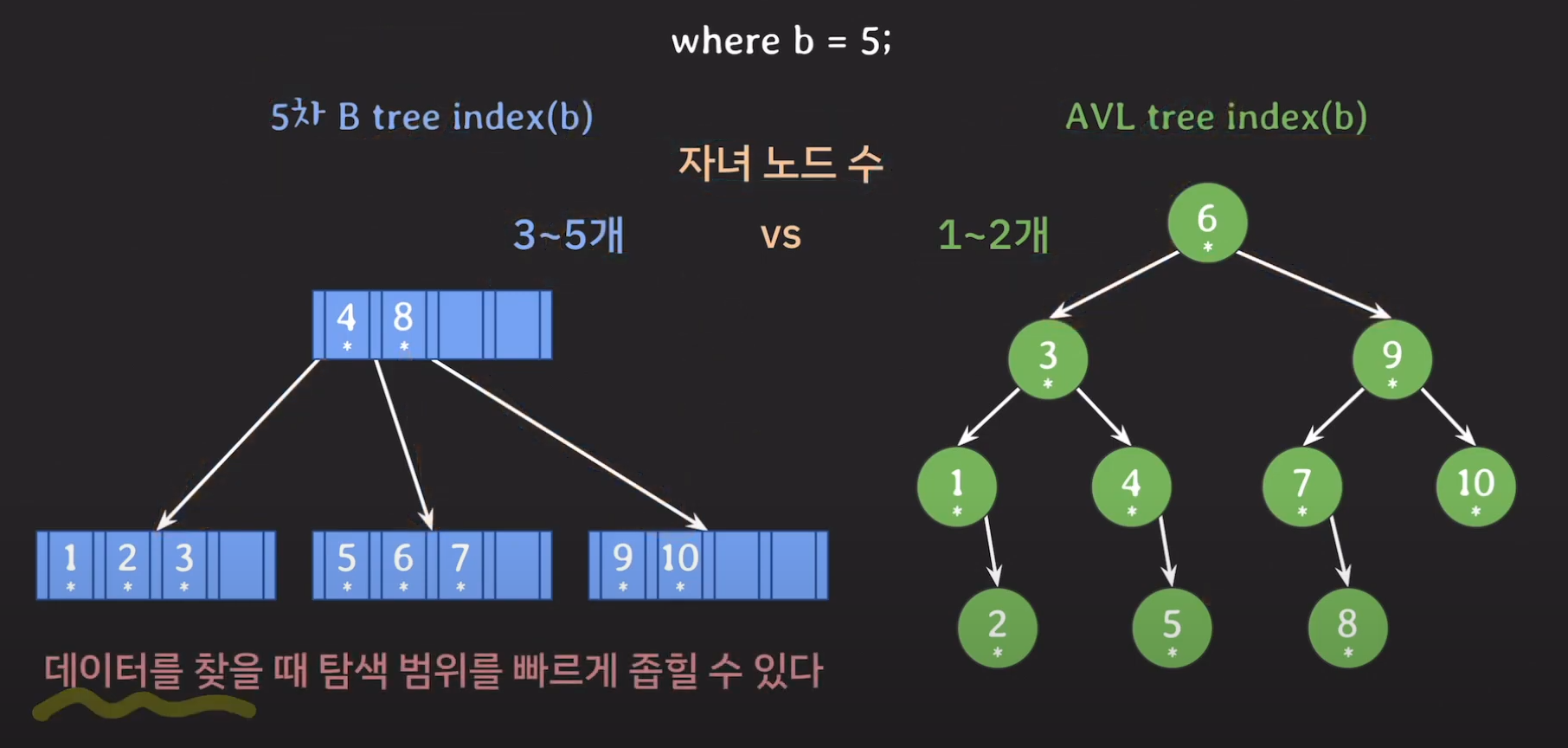
자녀 노드 수를 비교했을 때 B tree기반의 인덱스는 3~5개를 갖는 반면 AVL Tree는 1~2개의 자식만 갖게 됩니다. 따라서 AVL Tree의 경우 왼쪽 혹은 오른쪽으로 밖에 갈 수 없으므로 탐색 범위가 절반씩 줄어들게 됩니다.
반면에 B tree의 경우 최소 3개의 자식을 갖기 때문에 탐색의 범위를 1/3씩 줄여 나갈 수 있고 최대 1/5로 줄여 나갈 수 있게 됩니다.
결과적으로 B tree가 AVL tree에 비해 탐색 범위를 빠르게 좁힐 수 있습니다.
또한 B tree를 사용했을 경우 추가적인 장점이 존재합니다.
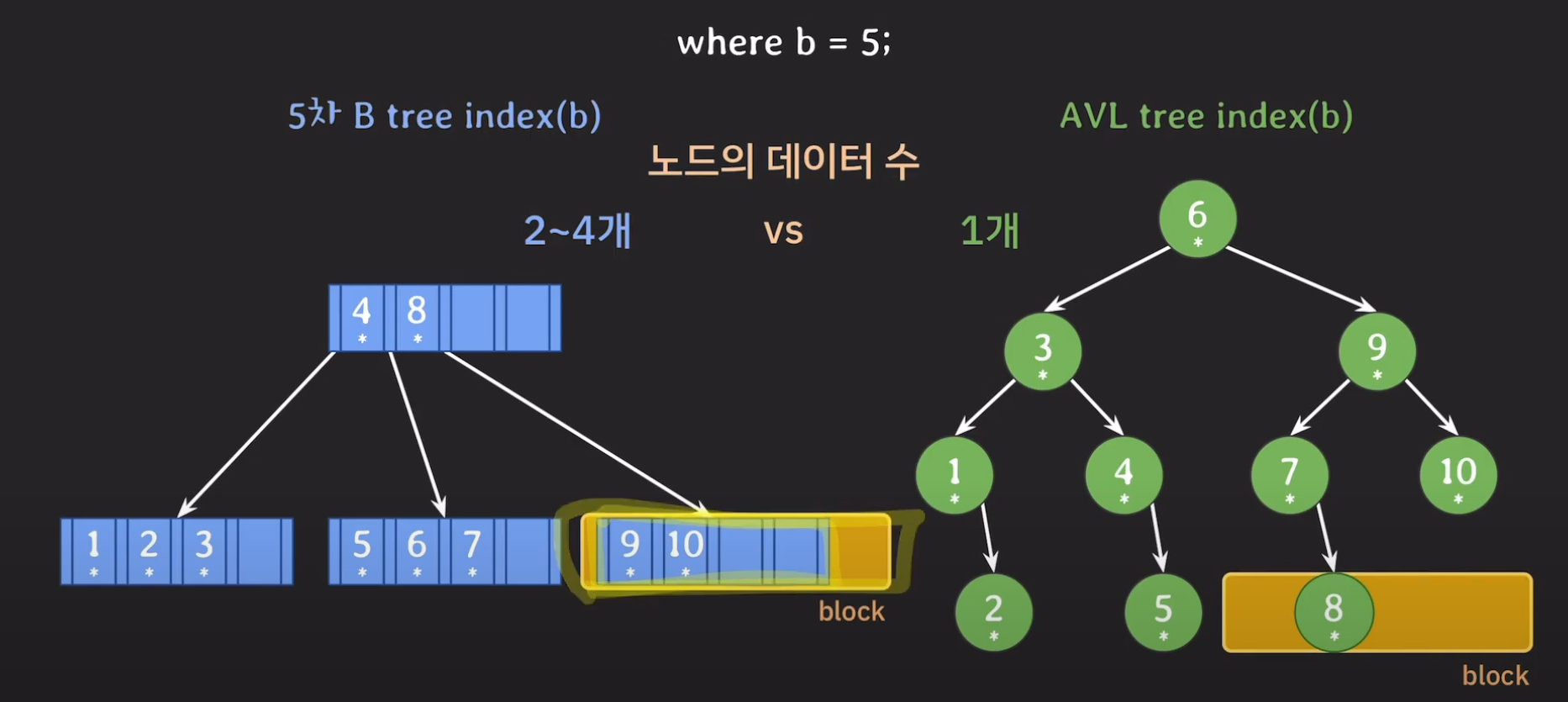
바로 노드의 데이터 수의 차이 때문입니다.
우리는 Secondary Storage에서 데이터를 block 단위로 읽어오는 것을 알고 있습니다.
AVL tree에 경우 8의 데이터를 읽어온다고 했을 때 필요없는 데이터를 함께 읽어오게 됩니다.
반면에 B tree에서는 한 노드에서 2~4개의 데이터를 가지고 있기 때문에 block 단위로 데이터를 읽어왔을 때 추가로 사용될 데이터도 미리 가져올 수 있게 됩니다.
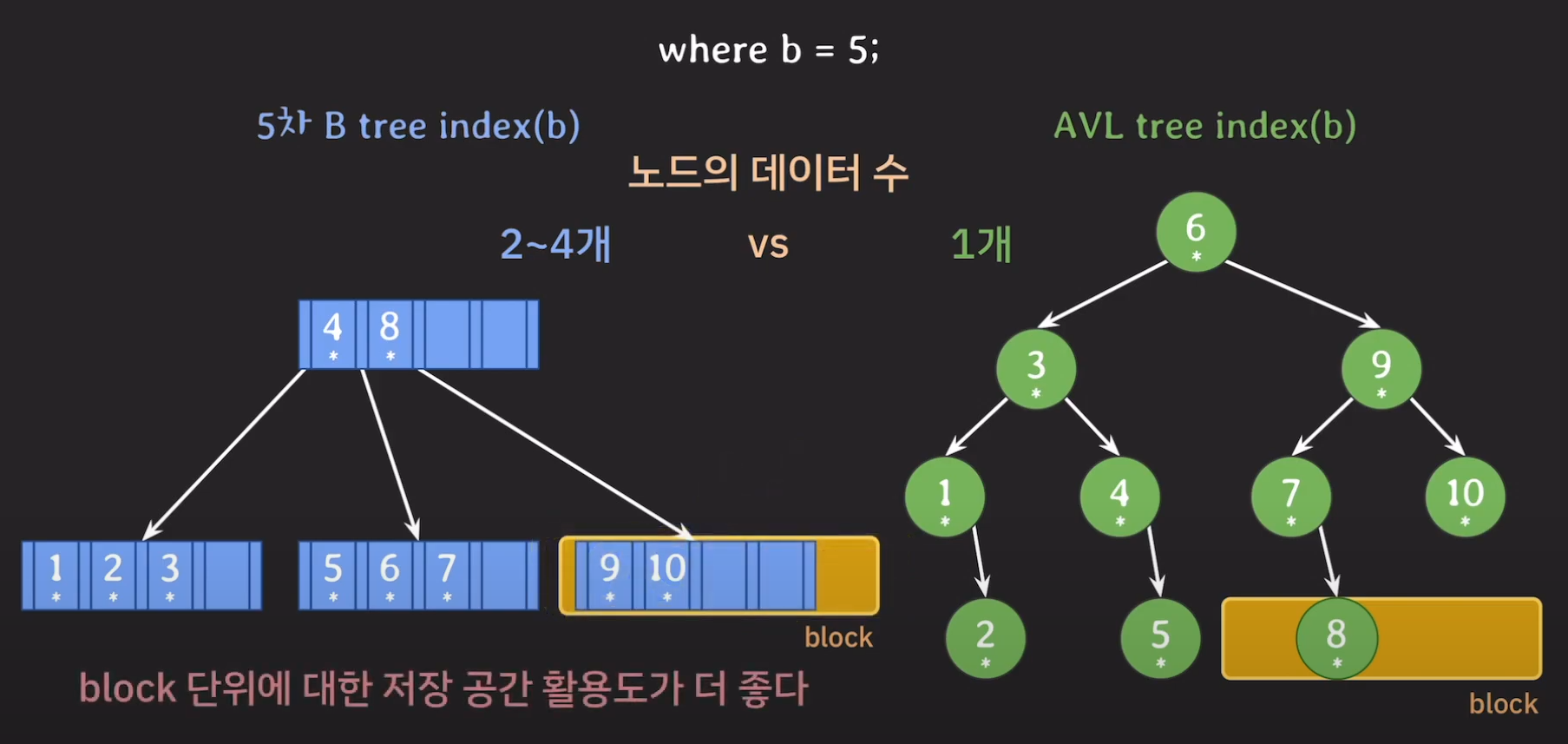
결론적으로 block 단위에 대한 저장 공간 활용도가 더 좋아집니다.
B tree의 강력함 With 101차 B tree

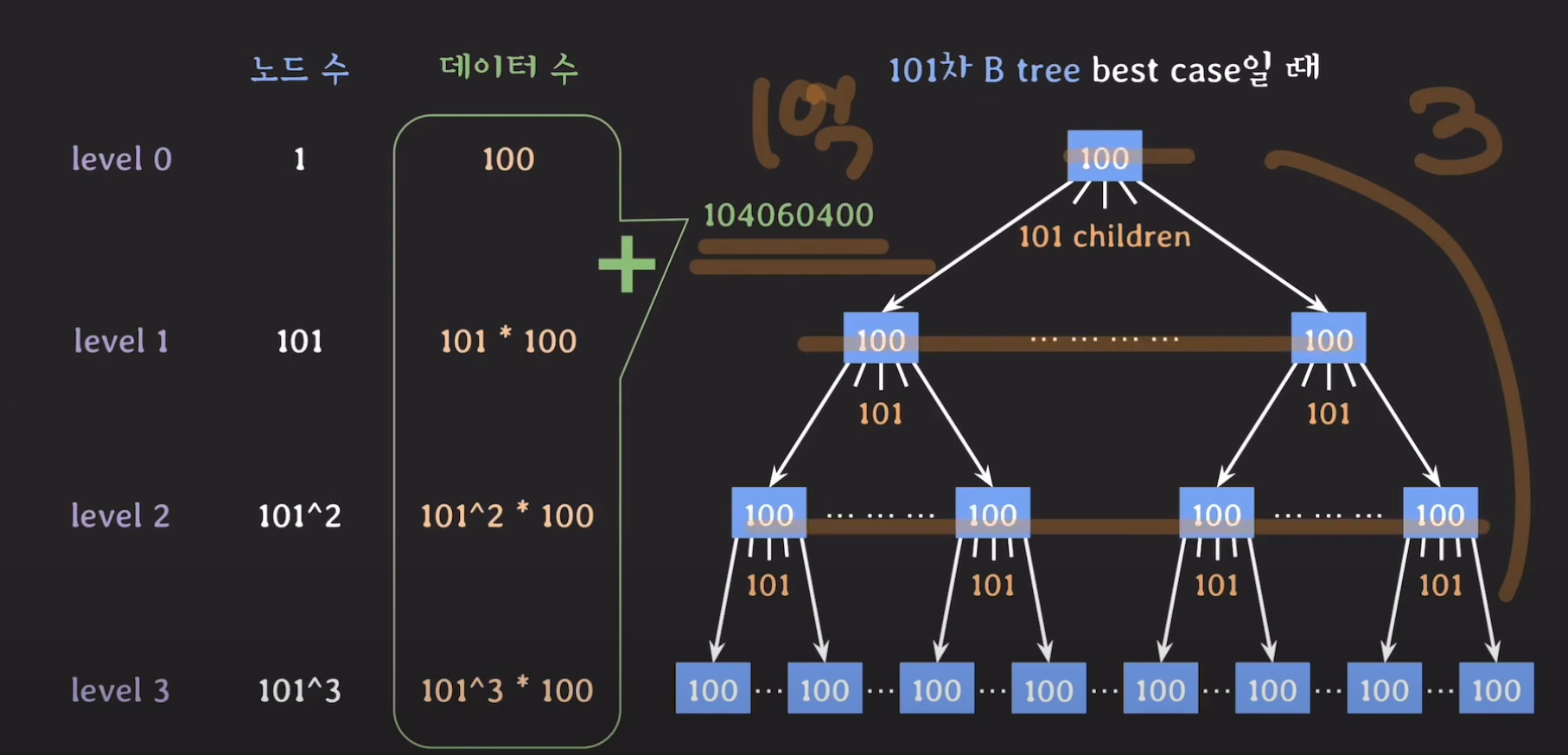
101차 B tree의 경우 높이가 3밖에 되지 않는데 1억개의 데이터를 저장할 수 있게 됩니다!

루트 노드는 최소 자녀수를 2개 가질 수 있으며 최소 key는 1개를 갖을 수 있습니다.
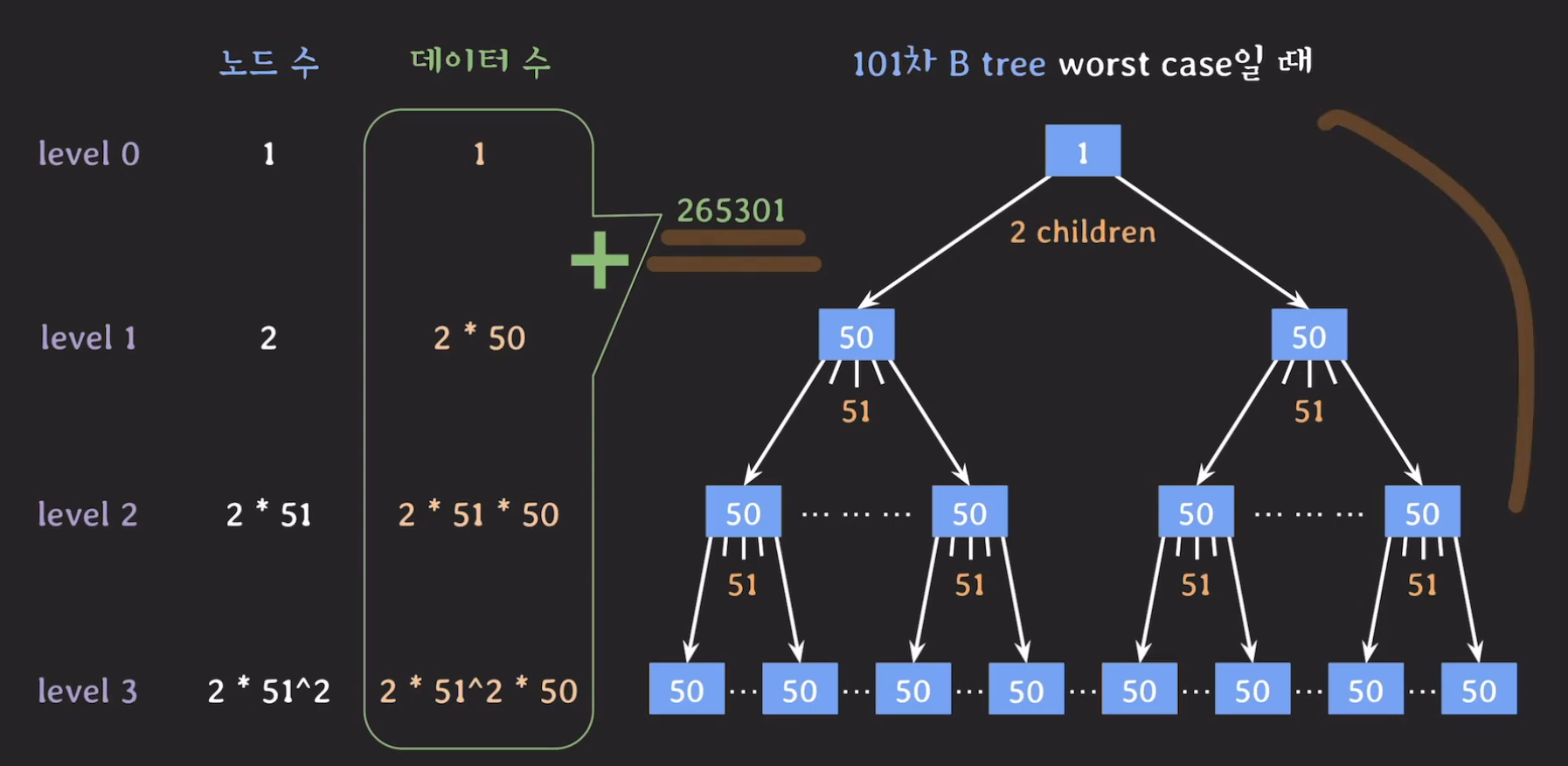
worst case의 경우에도 약 26만개의 데이터를 저장할 수 있습니다.
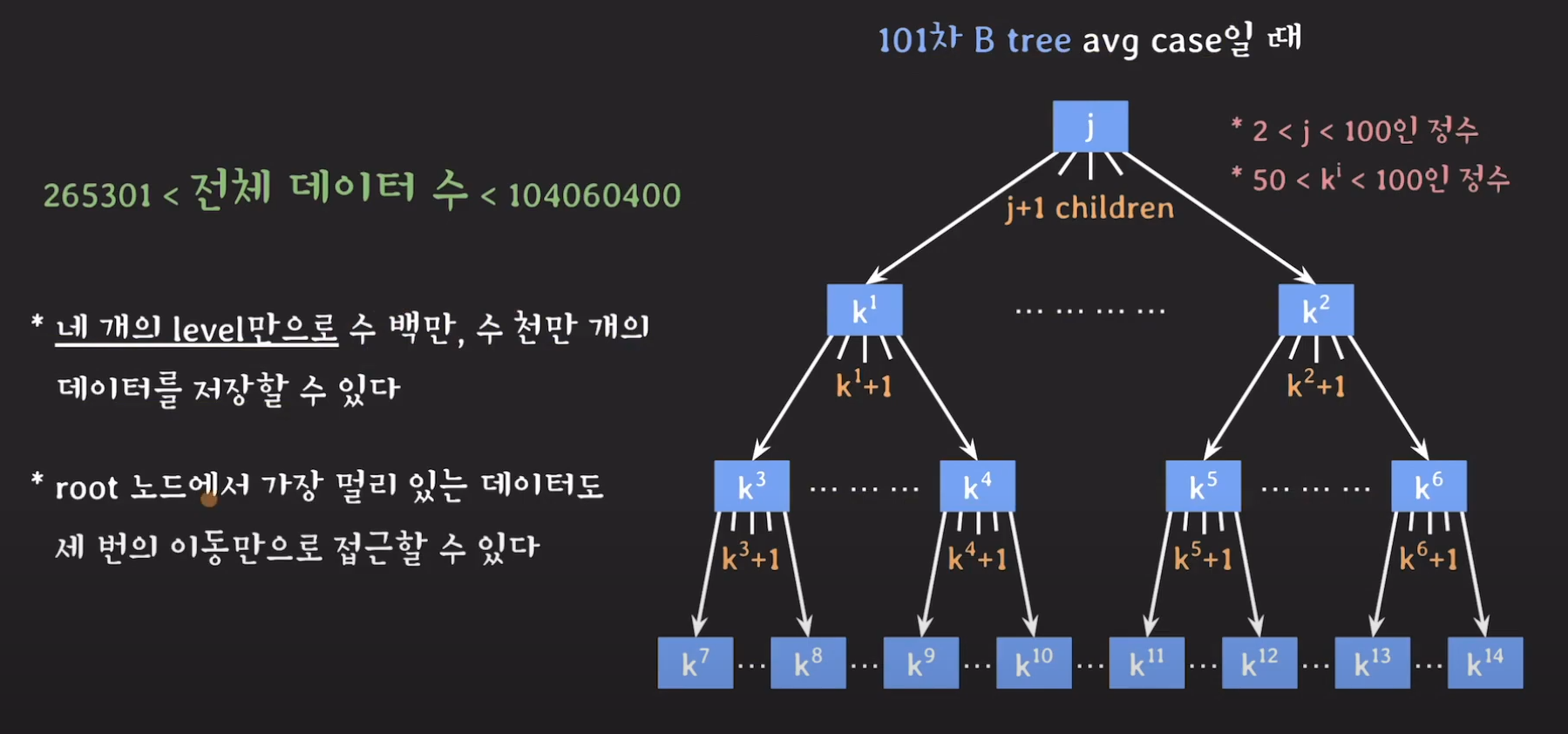
즉, 가장 멀리 있는 데이터를 3번의 Secondary Storage만 접근하면 되므로 성능상 큰 이점을 가져올 수 있습니다.
따라서 매무 많은 데이터를 저장하는 데이터베이스의 경우 B tree를 사용하는 것이 유리하단 사실을 유추할 수 있습니다.

DB는 기본적으로 Secondary Storage에 저장하므로 최소한으로 접근하는 것이 성능상으로 유리합니다.
두 번째와 세 번째 결론은 상호보완적이기도 합니다.
B tree 특성상 어떤 한 노드에 데이터를 x개 저장하면 자식의 수는 x+1개 저장할 수 있습니다. 즉, 한 노드에서 많은 데이터를 저장할 수 있다는 말은 한 노드에서 여러 자식을 가질 수 있다는 이야기며 데이터를 조회할 때 탐색 범위를 더 빠르게 줄일 수 있으니까 결국 Secondary Storage에 접근하는 횟수를 줄일 수 있게 됩니다.
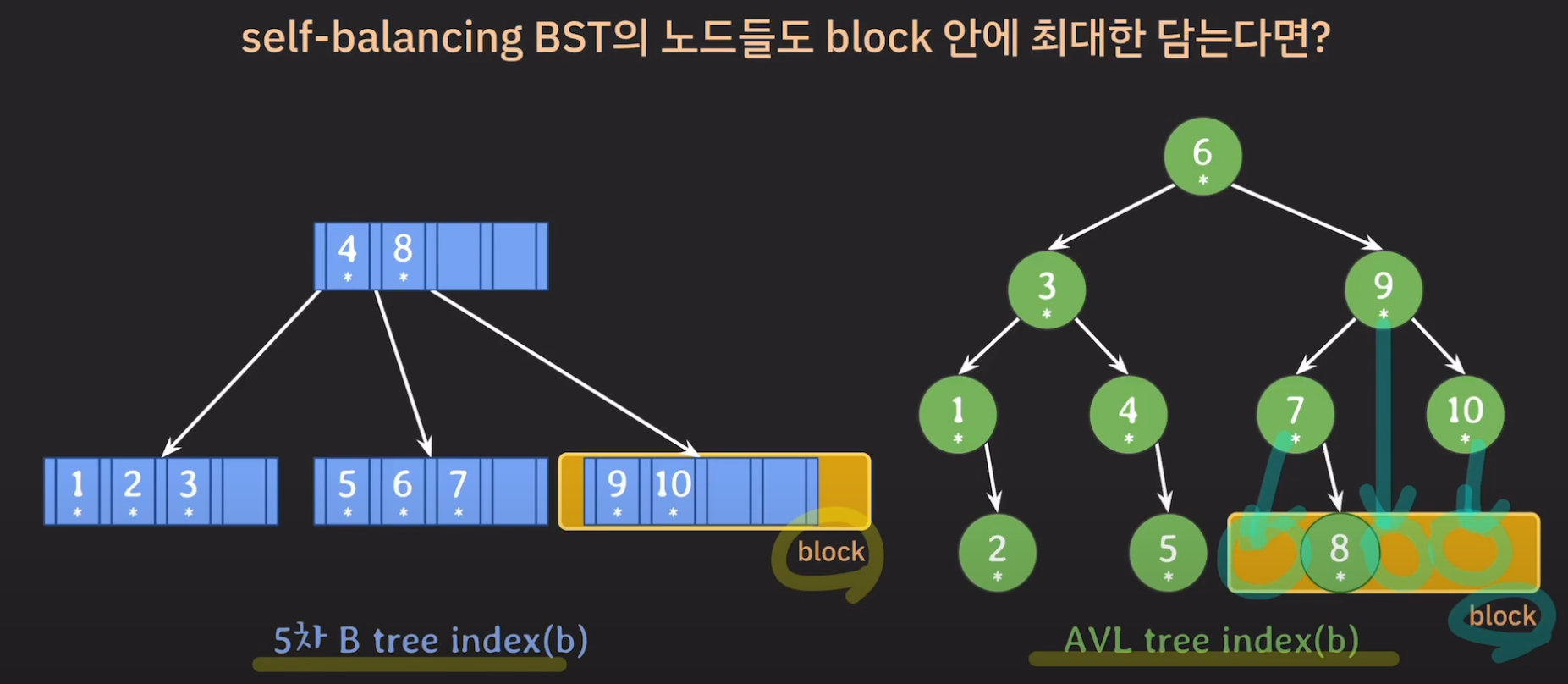
이런 고민을 할 수 있는데 이는 결국 B tree가 동작하는 방식이므로 굳이 밸런스 트리의 데이터를 한 block안에 담으려고 노력하지 말고 B tree를 사용하면 됩니다.

mysql에서도 실제로 hash index를 지원합니다. 만약 equality 조회만 하고 범위 검색이나 정렬에 사용할 일이 앞으로도 절대 없다라고 한다면 hash index를 사용하는 것이 성능상으로 좋습니다.
그러나 일반적으로 이런 일은 거의 없으므로 B tree를 사용한다고 생각하면 됩니다.
참고자료
쉬운코드 유튜브

