✏️ AVL Tree 개념
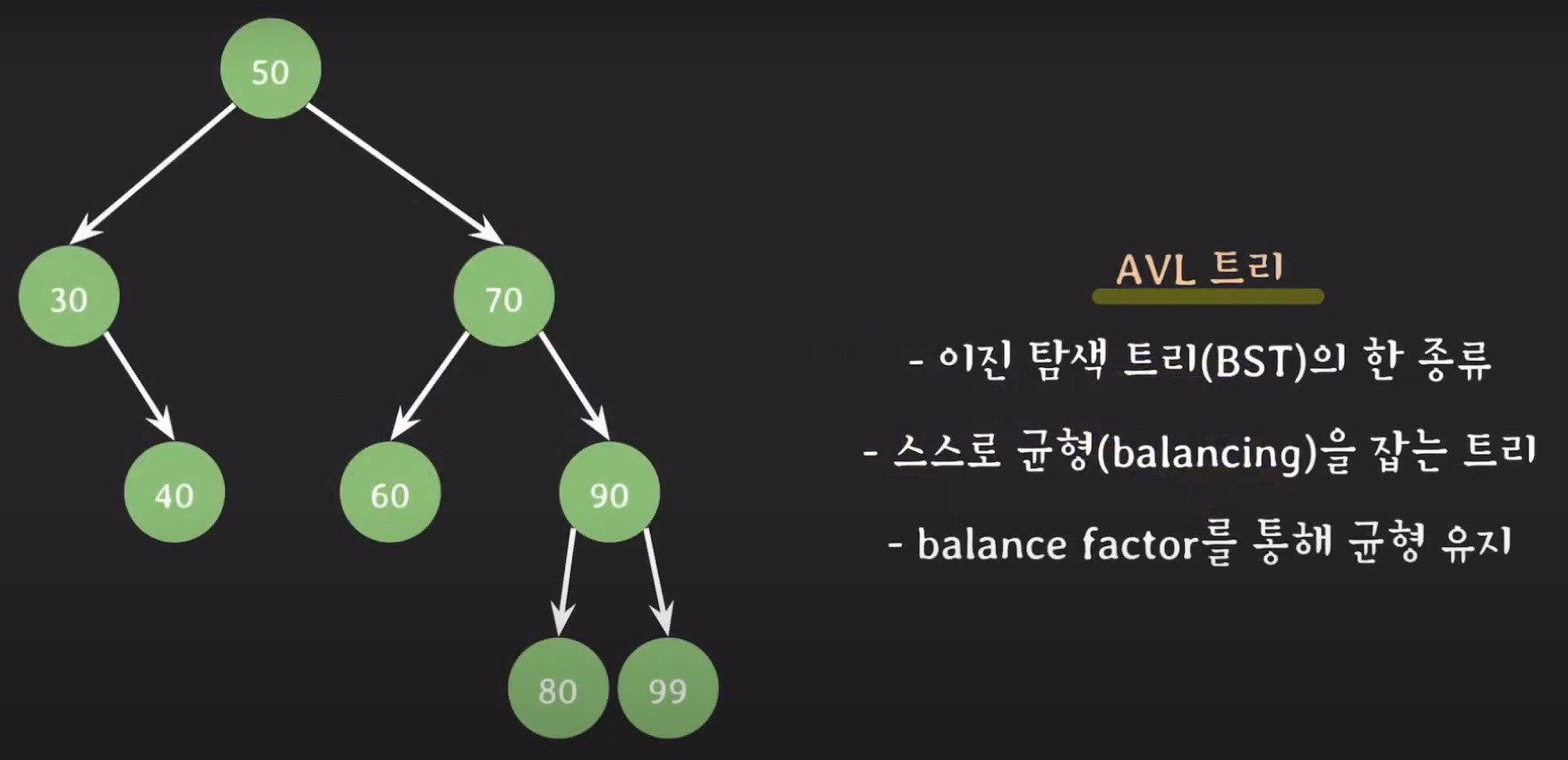
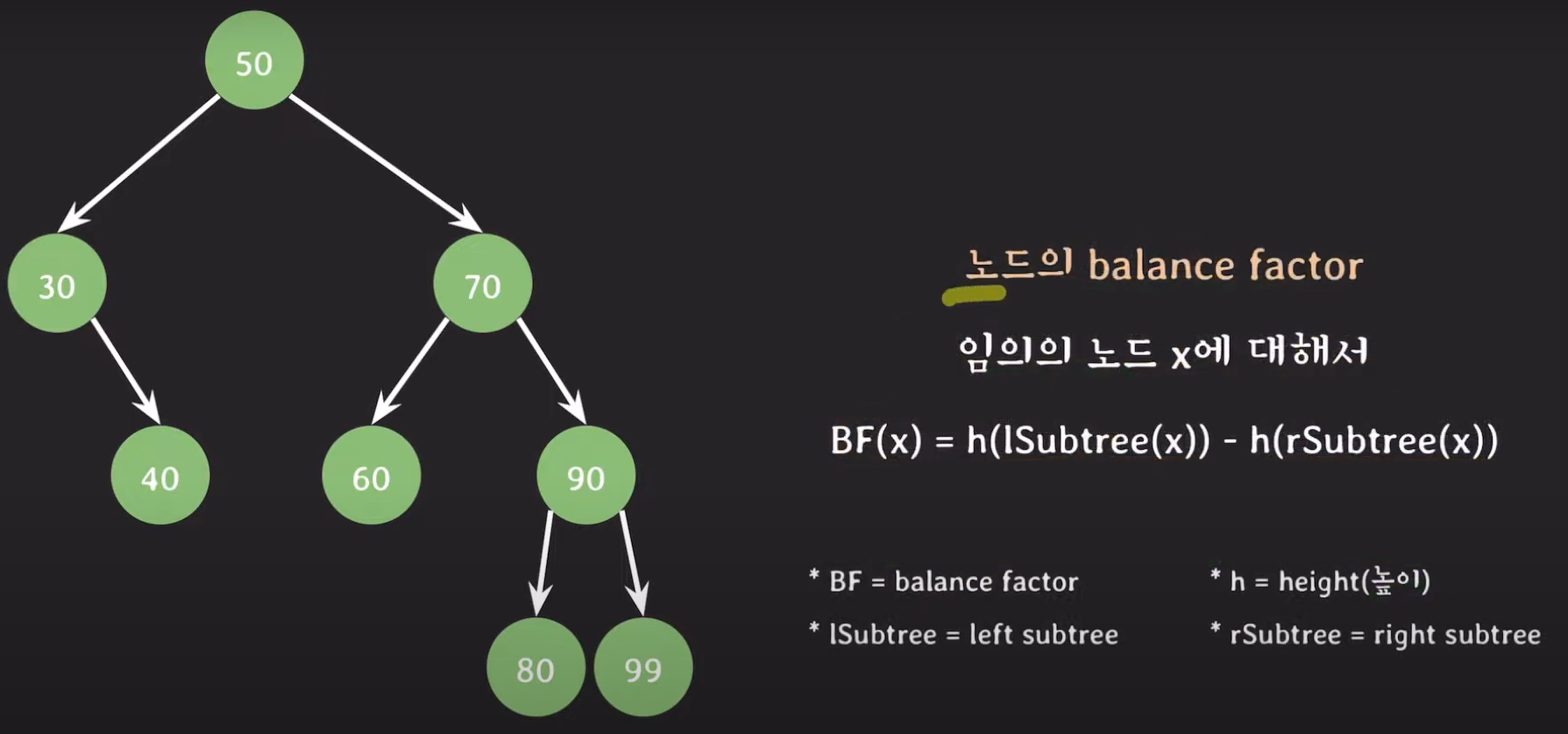
- balance factor란 오른쪽 서브 트리의 높이와 왼쪽 서브 트리의 높이차를 말합니다.
- 50을 기준으로 balance factor는 -1이 됩니다.
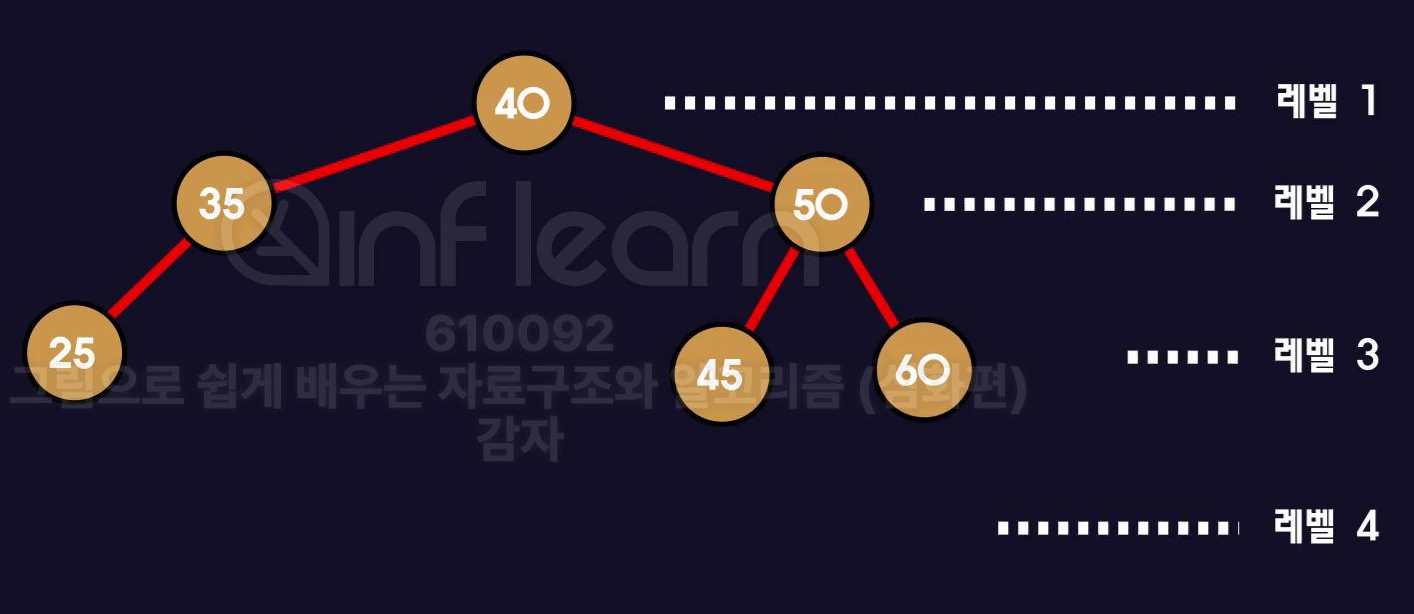
지난 시간에 Binary Tree의 시간 복잡도는 O(logn) 걸린다고 했지만 사실 아닙니다. 아래와 같은 상황이라면 logn이 아니라 O(n) 만큼의 시간복잡도를 가질 수 있다는 것을 생각해 볼 수 있습니다.
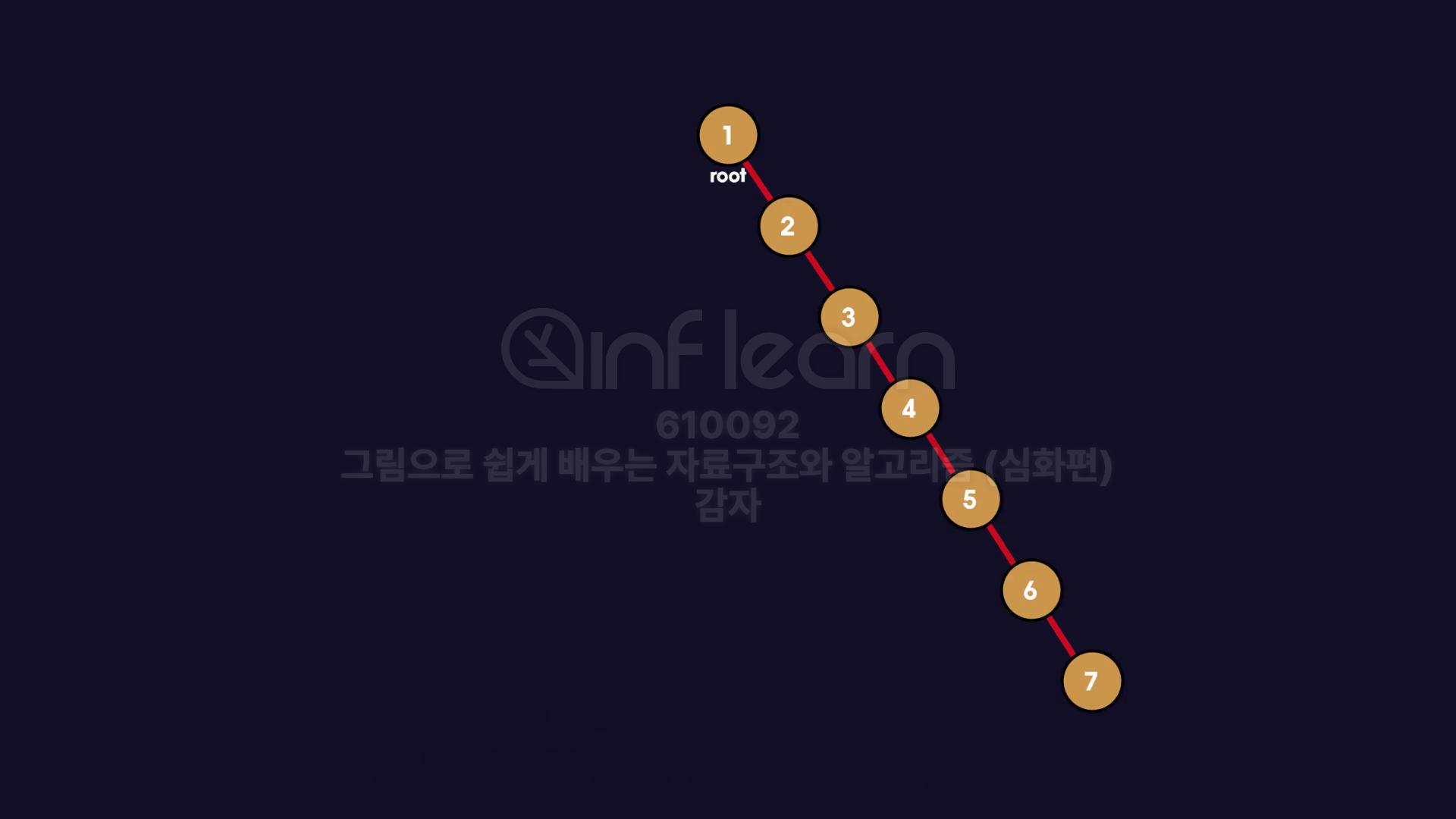
만약 균형 잡힌 이진 탐색 트리였다면 7을 검색하는데는 3번 즉 logn의 시간복잡도를 갖게 됩니다.
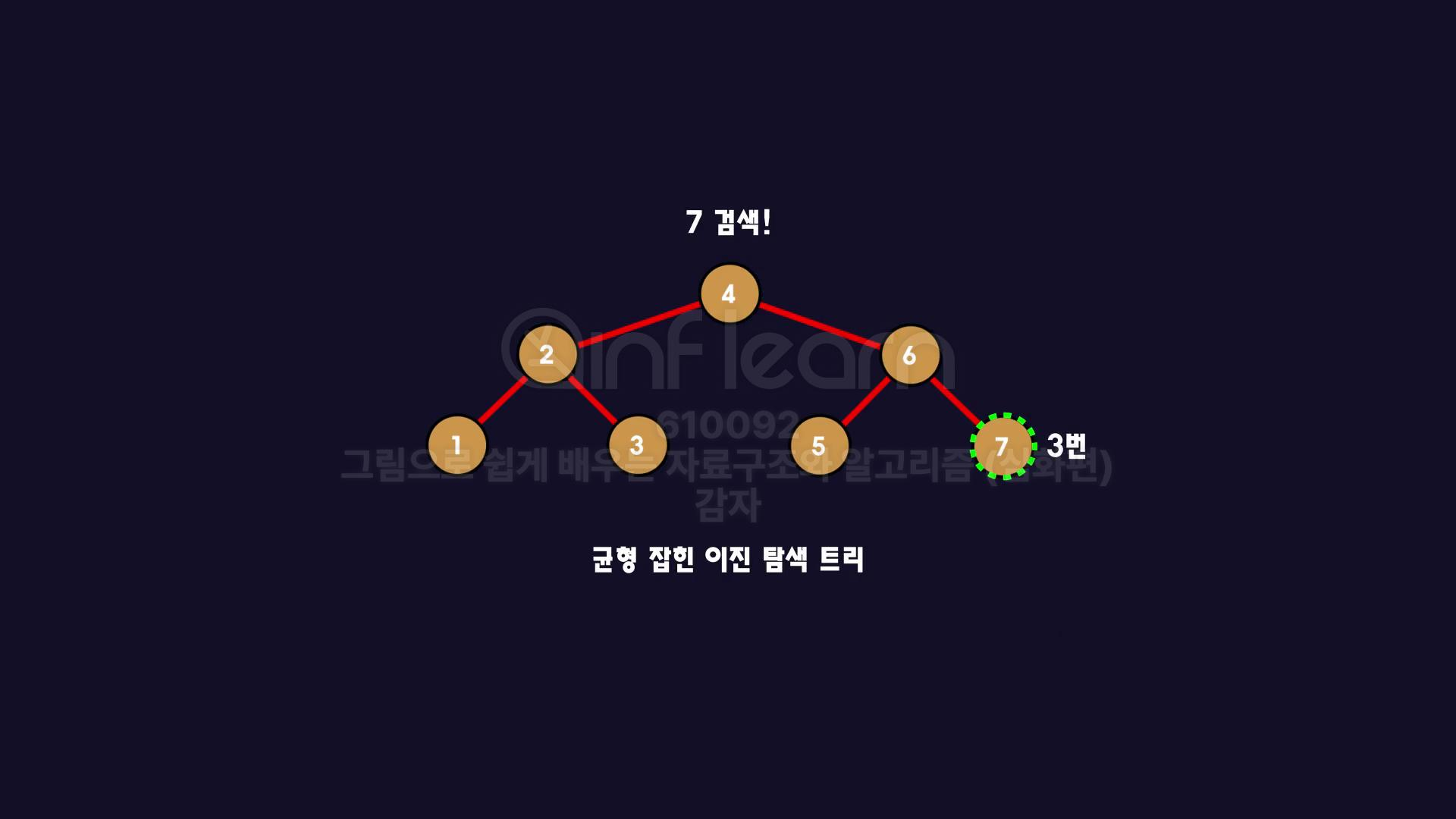
7번과 3번 별 차이 없는 것 같지만 데이터가 많이 늘어난다면 어떻게 될까요?
데이터가 40억개라고 가정하면 처음 상황에 경우 40억번을 검색해야 하고 균형 잡힌 경우라면 32번만에 찾을 수 있습니다.
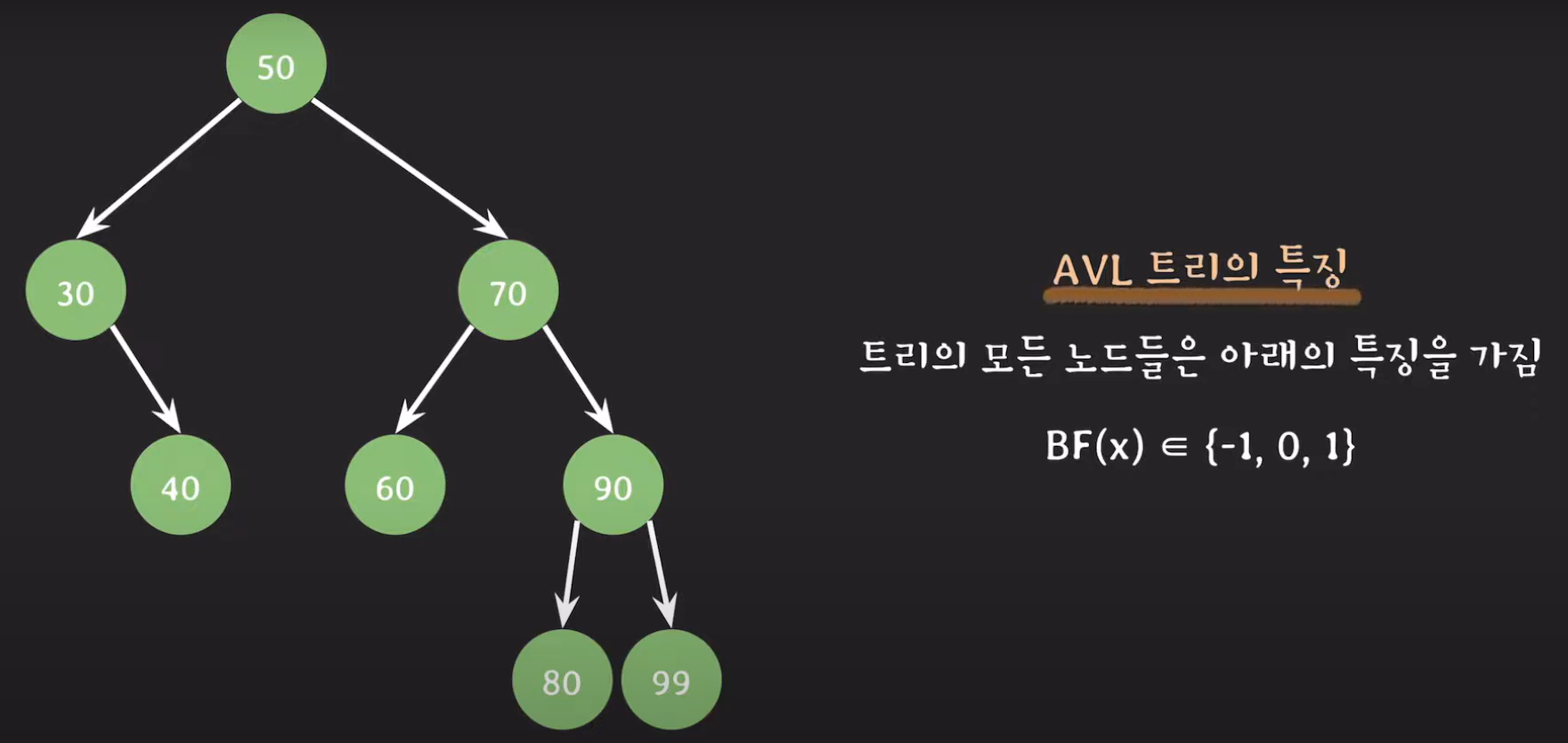
지난 시간에 배웠다시피 균형이 잡혔다는 것은 오른쪽 서브트리와 왼쪽 서브트리의 높이 차이가 1이하일 경우 균형 잡힌 트리였습니다.
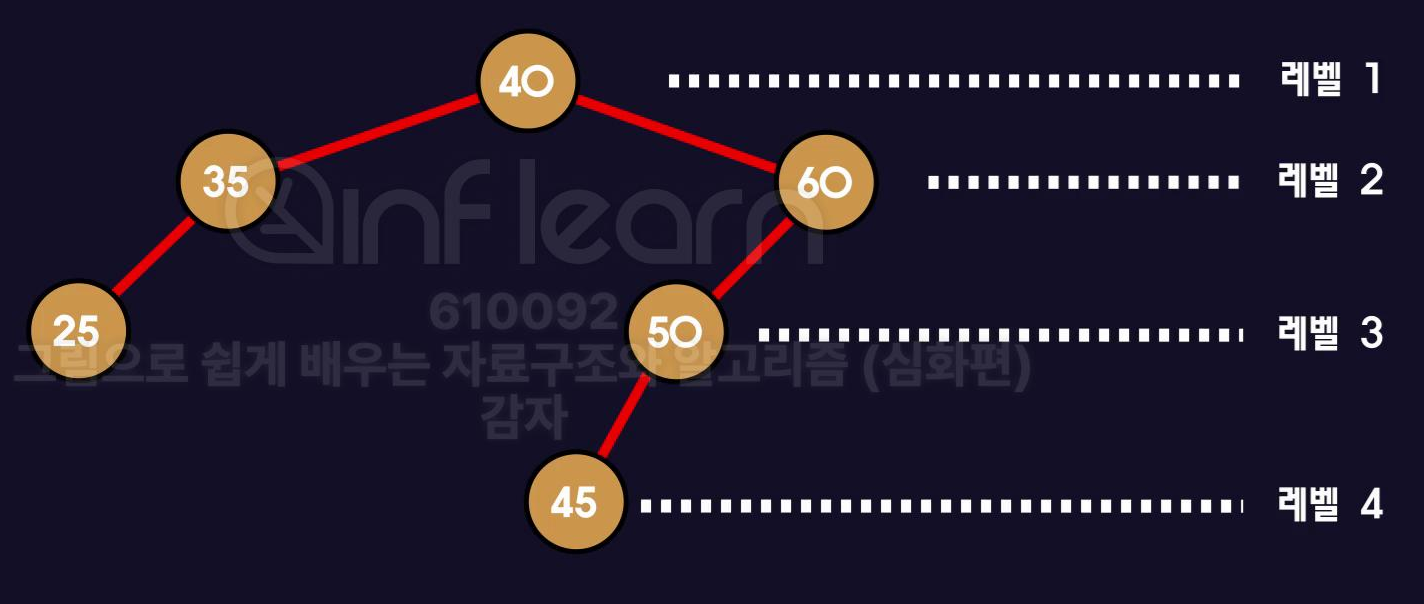
현재 이 트리는 균형이 맞지 않은 트리입니다.
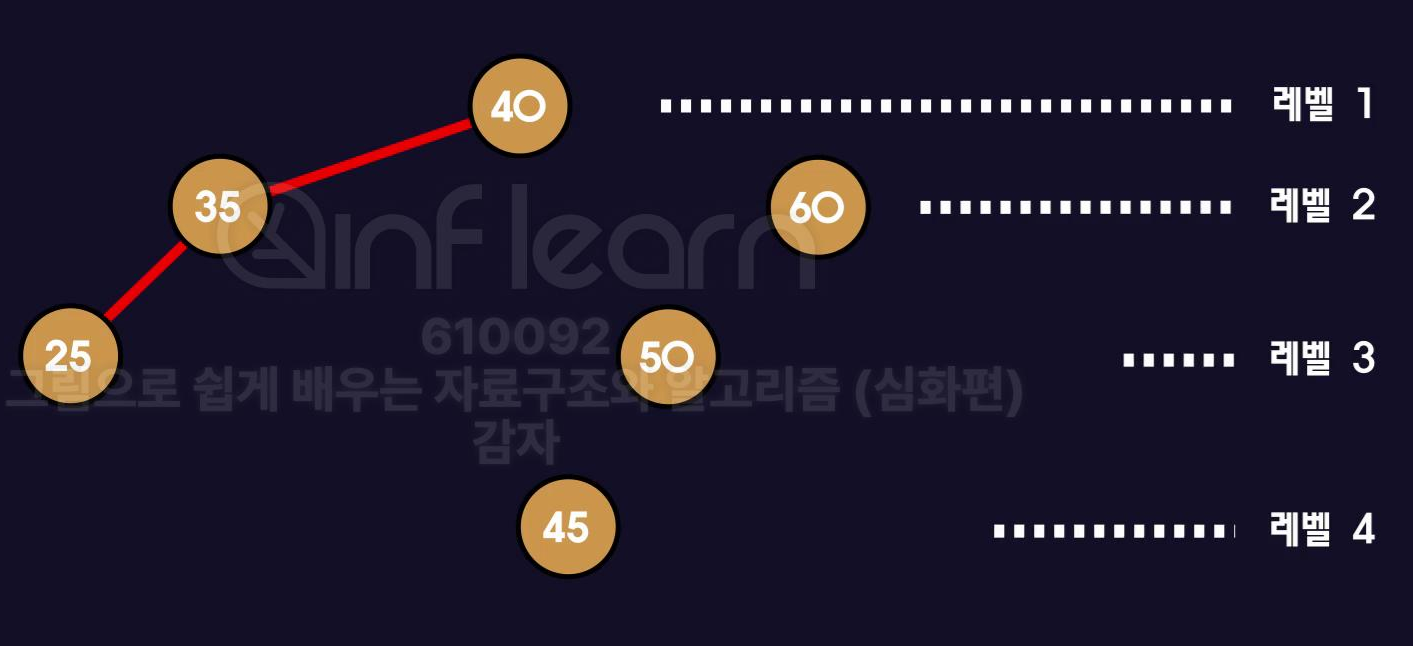
60을 다음과 같이 오른쪽으로 회전시켜주면 균형 잡힌 트리가 완성됩니다.
하지만 무조건 오른쪽으로 회전하면 되는 것은 아닙니다. 상황에 따라 여러 회전이 존재하며 이제부터 어떻게 회전해야 균형 잡힌 트리로 만들 수 있는지 알아보겠습니다.
회전의 종류
- LL 회전(Left Left Rotation)
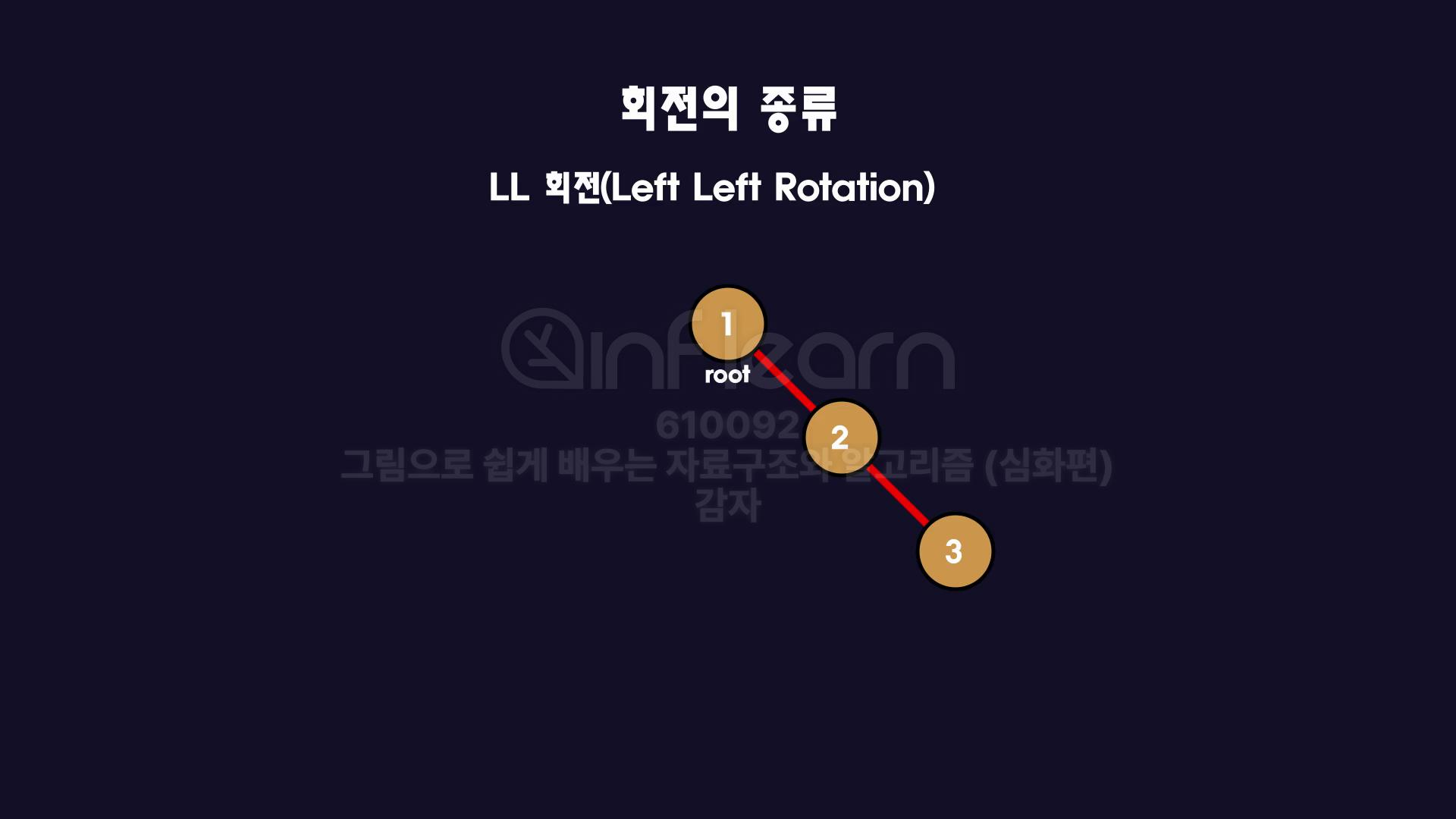
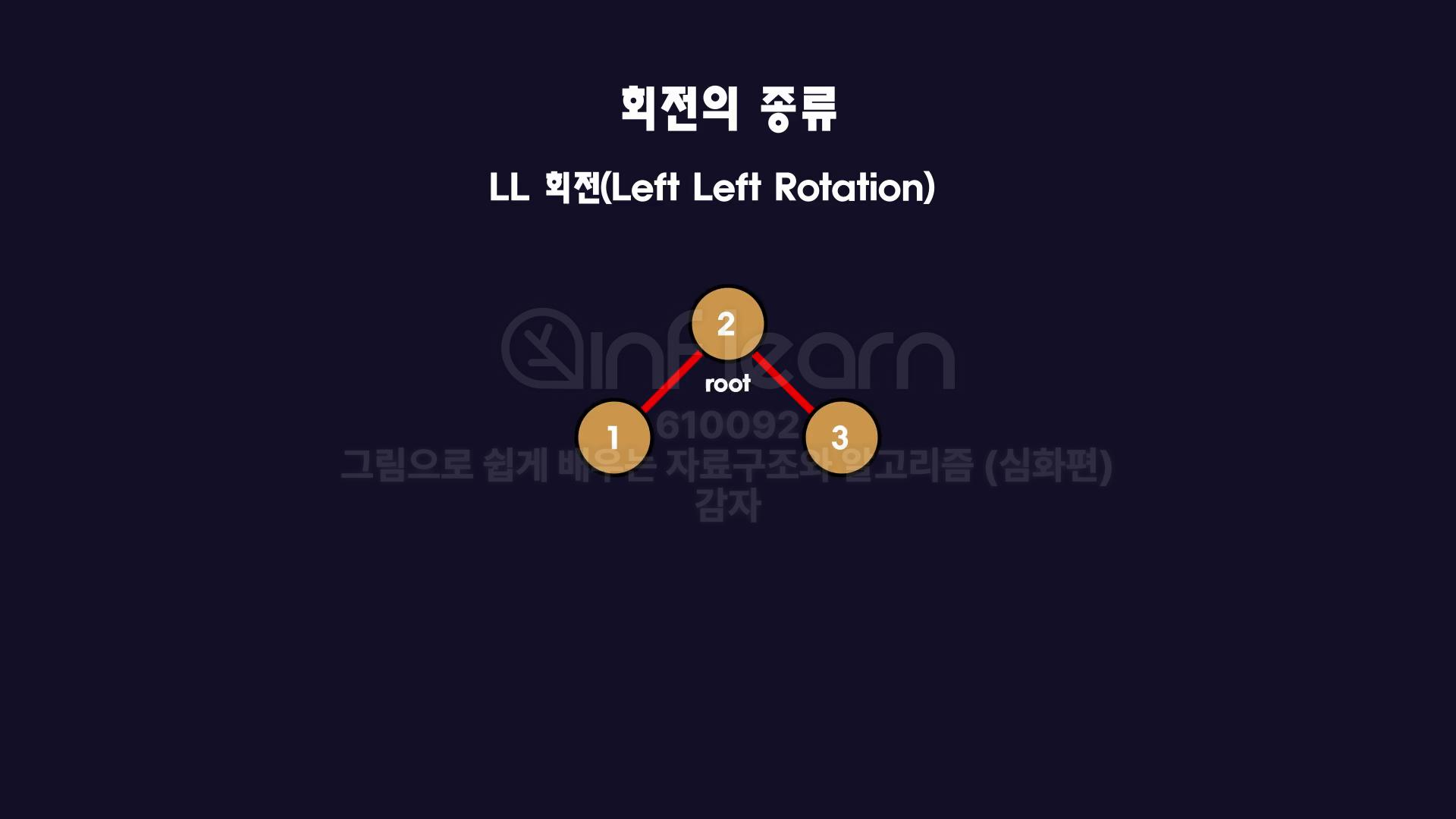
이런식으로 오른쪽으로 쭉 뻗은 상황이라면 root 노드를 반시계 방향, 즉 왼쪽으로 회전하게 되면 균형을 이룹니다.
- RR 회전 (Right Right Rotation)
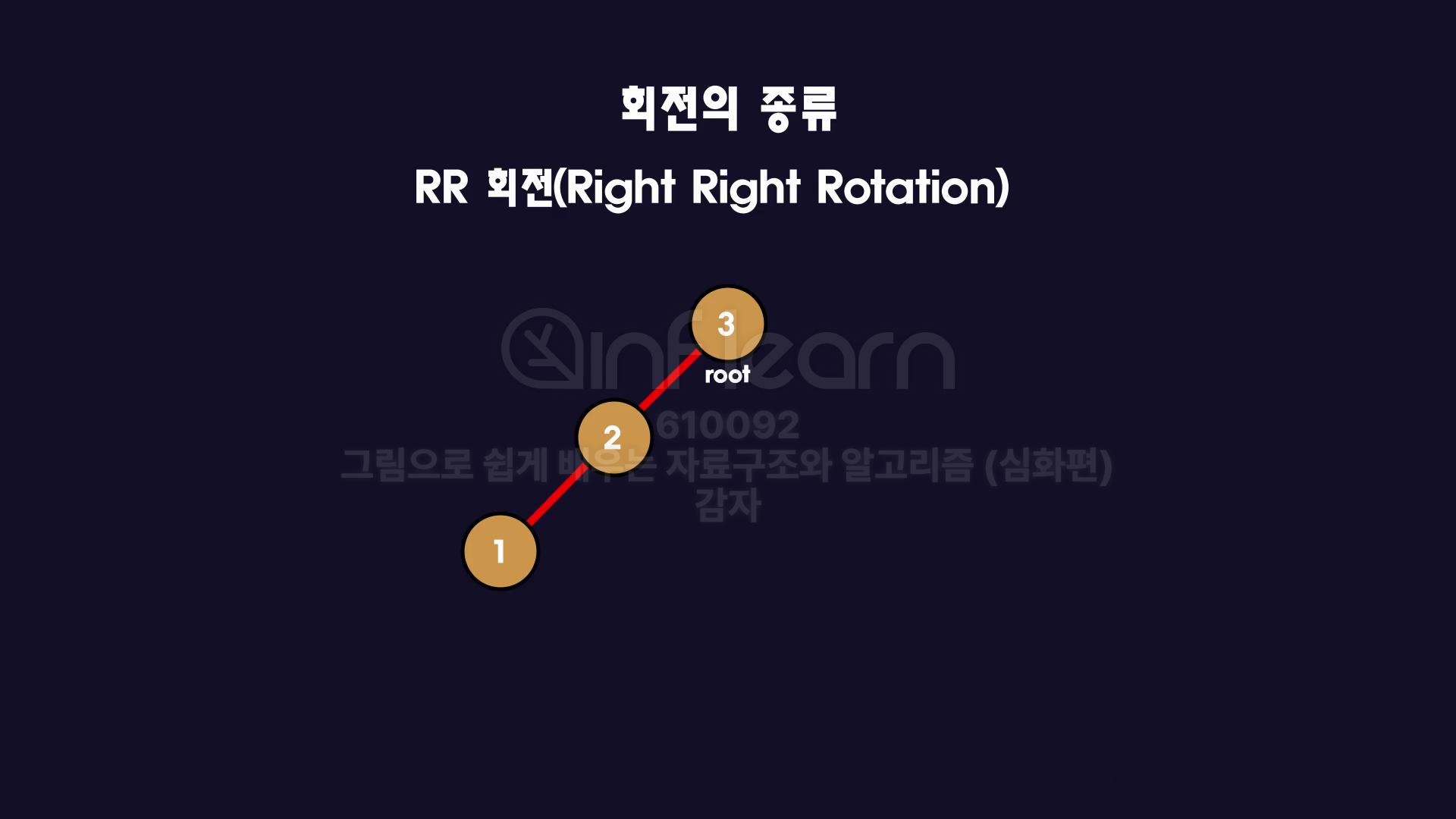
왼쪽으로 쭉 뻗은 경우 RR 회전이 필요합니다.
root 노드를 오른쪽으로 회전하게 되면 균형이 맞습니다.

- LR 회전 (Left Right Rotation)

중간에서 안쪽으로 꺾인 경우 LR 회전이 필요합니다.
이런 경우 1을 왼쪽으로 한 번 회전시켜 줍니다.


이 구조는 이전에 보았던 RR 회전이 필요한 경우이니 root를 오른쪽으로 한 번 회전시켜주면 됩니다.

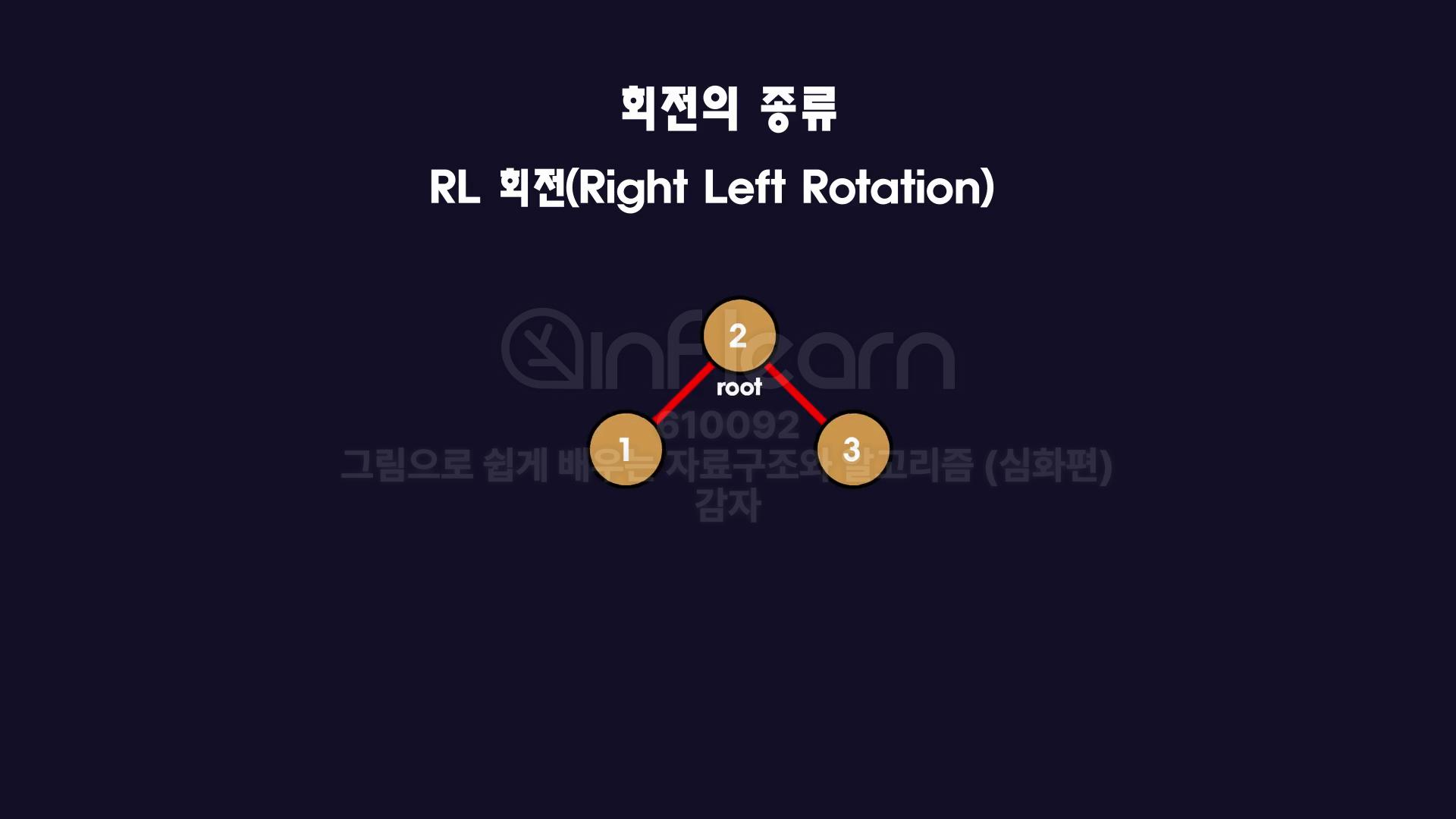
- RL 회전 (Right Left Rotation)
이번엔 오른쪽으로 꺾였다가 안쪽으로 꺾인 구조입니다.

이 경우 3을 오른쪽을 회전시켜줍니다.


첫 번째 상황과 같은 상황이므로 root를 왼쪽으로 회전시켜줍니다.
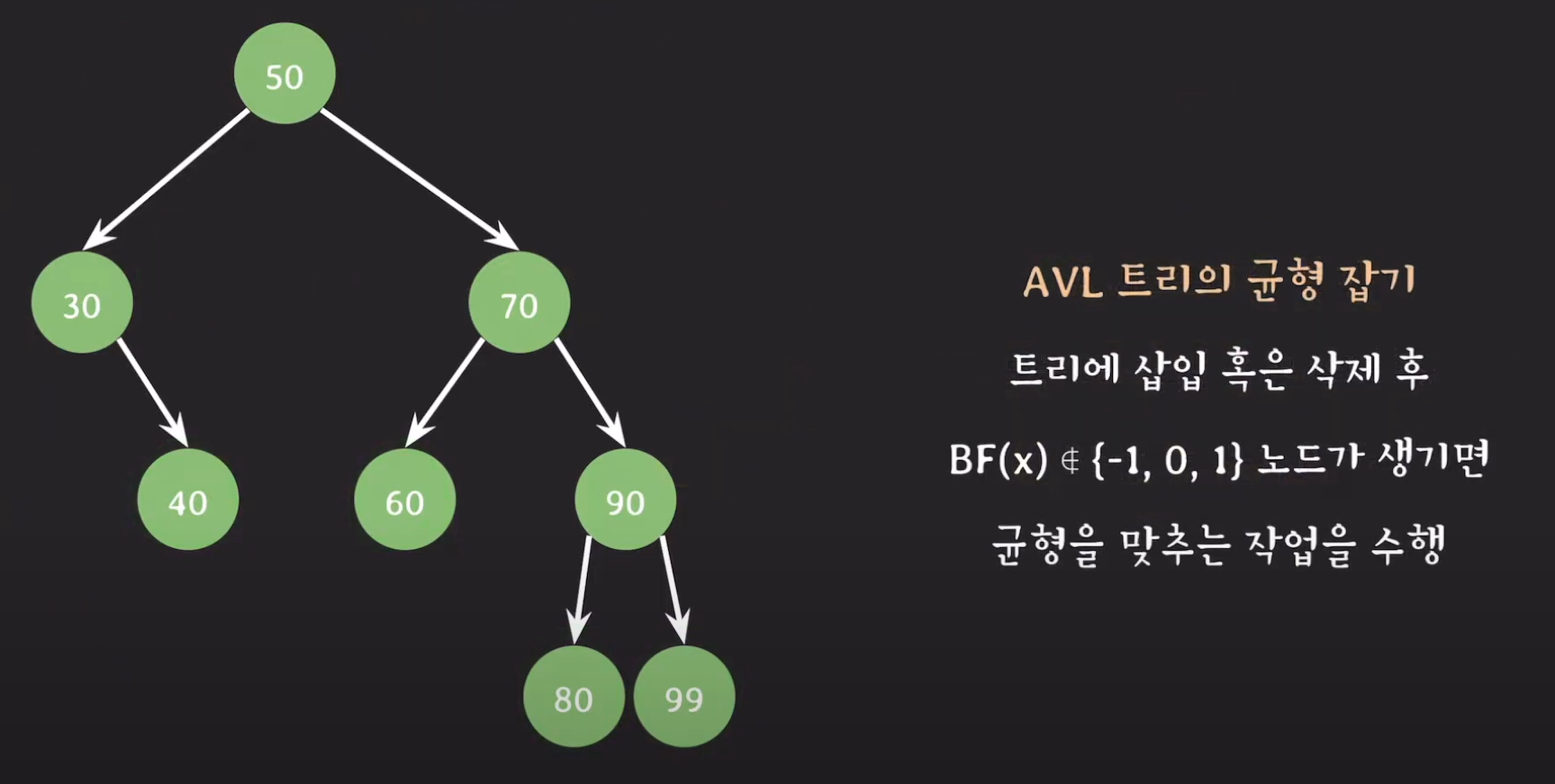
삽입/삭제가 발생한 위치에서 루트 노드로 거꾸로 올라오면서 BF를 확인하여 균형이 깨졌다면 재조정 해주어야 합니다.

최종적으로 AVL 트리는 위와 같은 시간복잡도를 갖습니다. 이전의 이진 탐색 트리의 경우 최악의 경우 O(n)이었지만 AVL 트리는 O(logN)으로 개선된 것을 확인할 수 있습니다.
그러나 엄격하게 균형을 유지하기 때문에 삽입/삭제 시 트리 균형을 확인하고 만약 균형이 깨졌다면 트리 구조를 재조정 하기 때문에 이 때 시간이 꽤 소요됩니다.
따라서 이 문제를 해결하는 것이 Red-Black Tree이다.
✏️ Trie Tree 개념
Trie는 자동완성 기능을 구현할 수 있는 최고의 자료구조라고 볼 수 있습니다.
Trie는 이진트리가 아닙니다. 따라서 자식노드의 수가 3 이상이 될 수 있습니다.
Trie는 저장하려는 단어를 한 글자씩 나눠서 해시 테이블을 사용해 키의 글자를 value에 자식노드를 저장합니다. 이때 자식노드는 다음 글자를 나타냅니다. 초기엔 루트 노드의 해시 테이블은 비어있습니다.
고등어라는 글자를 저장한다고 가정해보겠습니다.
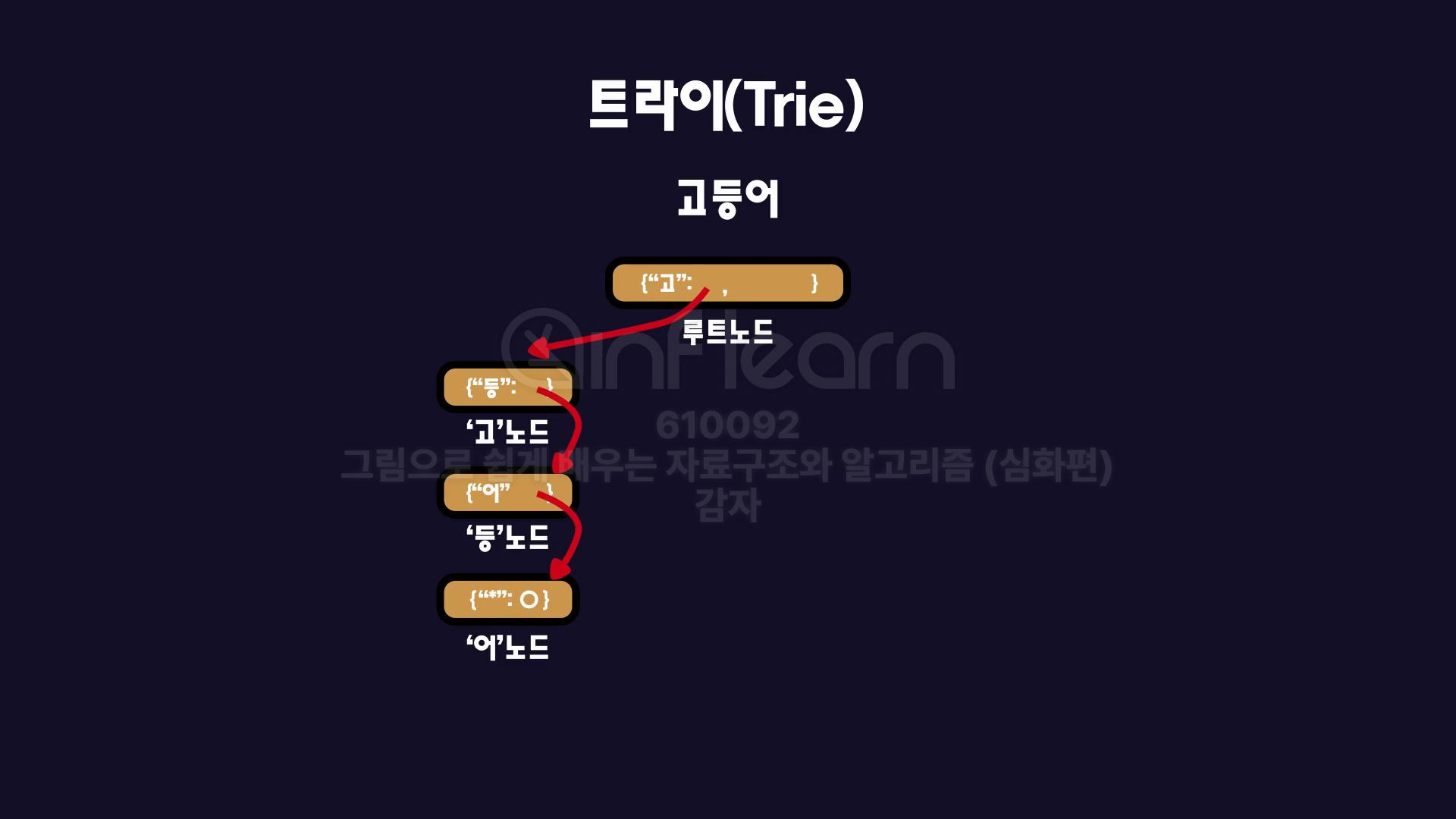
다음과 같이 각 노트에 key에는 글자를 value에는 자식 노드를 저장하는 것을 확인할 수 있습니다.
마지막에서는 Key에 Asterisk(에스타리스크)를 value에는 0을 저장합니다.
이때 Asterisk는 단어의 끝을 나타내며 value는 어떤값이든 저장하여도 상관없습니다.
같은 모습은로 '김치', '김치찜', '김치찌개'를 저장하면 다음과 같습니다.
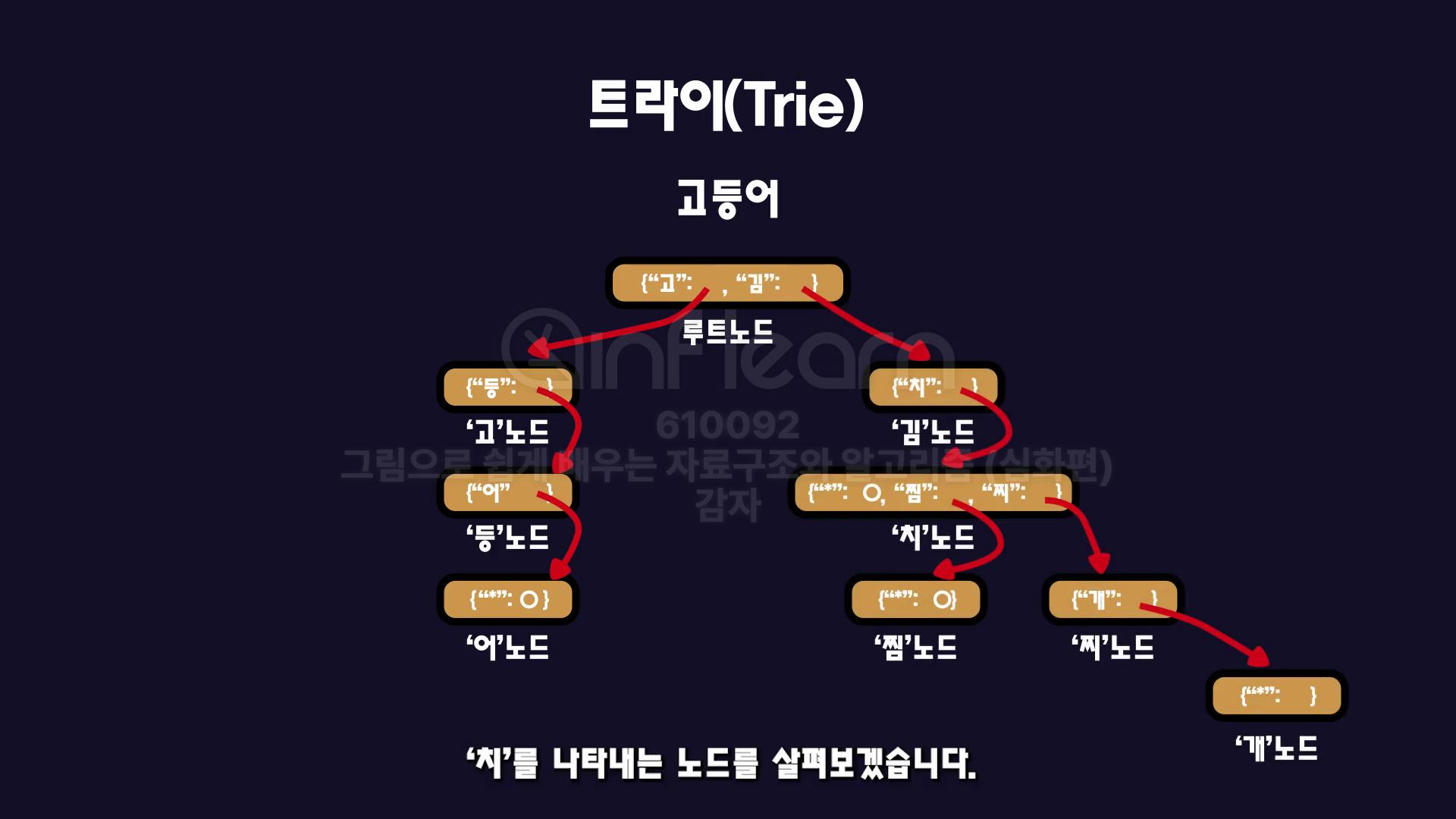
'치'노드에서 Asterisk가 존재하므로 치로 끝나는 단어가 존재한다는 것을 알 수 있습니다. 따라서 김치라는 단어가 존재함을 알 수 있습니다.
'찜' 노드에 Asterisk가 존재하므로 마찬가지로 김치찜이라는 단어가 존재함을 알 수 있습니다.
'개' 노드에는 Asterisk가 존재하지 않으므로 '개'로 끝나는 단어는 존재하지 않음을 알 수 있습니다.
이런식으로 저장된 Trie에서 김치를 검색하다고 가정해보겠습니다.
가장 먼저 루트 노드부터 순회하는데 루트노드에 김을 키로 가지고 있는지 알아봅니다. 만약 있다면 김에 해당하는 value로 이동합니다. 즉, '김' 노드로 이동합니다.
이제 '치'글자를 비교합니다. '김'노드에서 '치'를 키로 가지고 있는지 알아봅니다. 만약 있다면 '치'에 해당하는 value로 이동합니다.
이제 더 이상 비교할 글자가 없으니 마지막에 도착한 노드, 즉 '치' 노드에 Asterisk가 있는지 알아봅니다. 이 예시에서는 Asterisk가 존재하므로 '김치' 단어가 있다는 결론이 나옵니다.
Trie의 성능은 매우 우수합니다. 검색하려는 단어가 주어지면 한 글자를 하나씩 잘라서 해시테이블을 검색합니다. 이때 해시 테이블의 검색시간은 O(1)로 아주 빠릅니다. 그러므로 Trie의 단어가 수만가지 저장되어 있더라도 김치찌개를 검색했다면 단어의 수만큼인 4단계만에 찾을 수 있습니다.
하지만 그렇다고 해서 Trie의 검색 성능은 상수시간인 O(1)은 아닙니다. 글자수에 따라서 단계가 달라지기 때문이죠.
그럼 O(N)이라고 착각하기 쉽지만 여기서 N은 Trie의 저장된 노드수를 말합니다. 글자수와는 어면이 다릅니다.
따라서 글자수의 따라 성능이 결정된다고 해서 O(K)라는 표기를 사용합니다. 이때 K라는 문자 대신 N이 아닌 어떤 문자가 와도 상관없습니다.

