경사하강법은 머신러닝에서 가장 기본적인 최적화 알고리즘 중 하나다. 이 알고리즘은 비용 함수의 최솟값을 찾기 위해 모델의 가중치를 점진적으로 업데이트하는 방식으로 작동한다.
경사하강법을 사용하면 데이터를 표준화 또는 정규화하는 스케일링(scaling) 전처리가 중요하다. 이는 데이터의 크기를 일정한 스케일로 맞추는 작업을 말한다.
데이터를 정규화하면 경사하강법의 수렴 속도를 높이는 데 도움이 된다. 데이터가 정규화되지 않은 경우, 특정 특성의 크기가 다른 특성의 크기보다 훨씬 크면 그 특성이 경사하강법의 업데이트에 더 큰 영향을 미치게 된다. 이는 경사하강법이 최솟값에 도달하는 데 더 많은 시간을 소요하게 만든다.
데이터를 정규화하면 경사하강법의 수렴 속도를 높이는 데 도움이 되는 다음과 같은 이유들이 있다.
- 특성 스케일의 일관성: 데이터를 정규화하면 모든 특성의 크기가 일정한 스케일로 맞춰진다. 이렇게 하면 특정 특성의 크기가 다른 특성의 크기보다 훨씬 커서 경사하강법의 업데이트에 더 큰 영향을 미치는 것을 방지할 수 있다.
- 경사 분포의 개선: 데이터를 정규화하면 경사 분포가 더 균일해진다. 이렇게 하면 경사하강법이 모든 특성에 균등하게 업데이트를 적용할 수 있게 되어 수렴 속도를 높일 수 있다.
- 목적 함수의 매끄러움 증가: 데이터를 정규화하면 목적 함수가 더 매끄러워진다. 이렇게 하면 경사하강법이 목적 함수의 최솟값을 더 쉽게 찾을 수 있다.
- 초기 가중치에 대한 민감도 감소: 데이터를 정규화하면 초기 가중치에 대한 경사하강법의 민감도가 감소한다. 이렇게 하면 경사하강법이 초기 가중치의 선택에 덜 민감해져서 수렴 속도를 높일 수 있다.
다음의 그림을 보자.
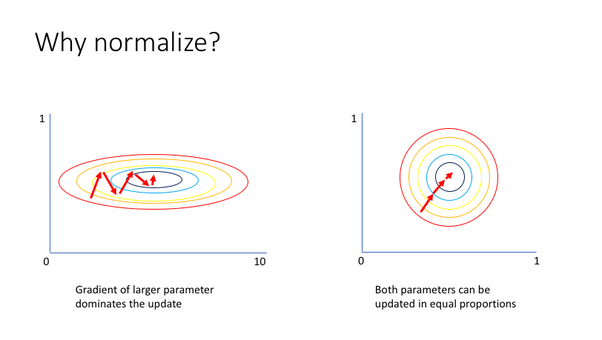
값이 큰 파라미터가 존재하면 왼쪽 그림과 같이 원의 커브(curvature)가 더욱 커져서 가중치의 업데이트 방향에 영향을 지나치게 많이 주게 된다. 반면 정규화를 한 데이터에서는 오른쪽 그림과 같이 모든 파라미터에 일정하게 가중치 업데이트가 이루어지기 때문에 더 효율적인 학습이 가능한 것이다.
다음은 numpy에서 정규화를 위해 사용되는 np.linalg.norm() 함수의 활용 예시다.
먼저, 다음과 같은 벡터 가 있다.
이때 아래의 함수를 활용해서...
벡터의 norm 값을 구할 수 있다.
또 하나의 스케일링 방법은 평균을 0으로 하고 표준 편차를 1로 맞추는 것이다. 이를 표준화(standardization)라고 한다.
다음은 데이터를 표준화하는 Python 코드의 예이다.
import numpy as np
# (가상의) 데이터를 로드한다.
data = np.loadtxt("data.csv", delimiter=",")
# 데이터의 평균값을 빼주고 표준편차로 나눠준다.
data = (data - data.mean(axis=0)) / data.std(axis=0)
# 데이터를 저장한다.
np.savetxt("data_normalized.csv", data, delimiter=",")이 코드는 data.csv 파일의 데이터를 읽어와 평균을 0으로 하고 표준 편차를 1로 맞춘 후 data_normalized.csv 파일에 저장한다.
데이터를 정규화하면 경사하강법의 수렴 속도를 높이는 데 도움이 될 수 있다. 따라서 머신러닝 모델을 학습할 때 데이터를 정규화하는 것을 고려하는 것이 좋다.
https://towardsdatascience.com/an-introduction-to-gradient-descent-c9cca5739307
https://www.quora.com/Why-does-mean-normalization-help-in-gradient-descent
