선형 모델만을 가지고는 복잡한 문제를 풀 수 없다.
신경망은 비선형 모델.
하지만 신경망을 수학적으로 뜯어보면 선형모델과 비선형모델의 결합들로 이루어져 있음.
오늘은 신경망을 수식으로 분해해보고, 선형 모델의 동작 방식, 신경망이 어떻게 선형 모델을 기반으로 비선형 모델과 결합할 수 있는지 알아보자!
신경망을 수식으로 분해해보기
가중치 행렬 W (다른 Data 벡터공간으로 보내주는 행렬)
아래는 전형적인 선형모델이다.
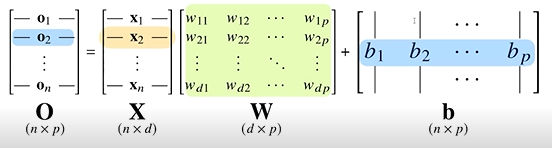
짧게 이야기하자면,
n x d, 즉 d차원에 존재하는 X라는 행벡터들을 W라는 가중치 행렬을 곱하고, b라는 행벡터들(y절편으로 이해하면 쉽다)더함으로써
n x p, 즉 p차원의 점들로 바꿔주는 모델이다.
Activation Function - 활성 함수
신경망은 선형모델과 활성함수를 합성한 함수이다.
활성함수를 이용해서 "선형모델"로 나온 출력물을 "비선형" 벡터로 바꿀 수 있고, 이렇게 변형시킨 벡터를 잠재벡터또는 히든벡터라고 한다.
활성함수는 실수값을 입력으로, 실수값을 출력으로 갖는 비선형 함수이다.
대표적으로 Softmax, Sigmoid, tanh(하이퍼볼릭탄젠트), ReLU가 있다.
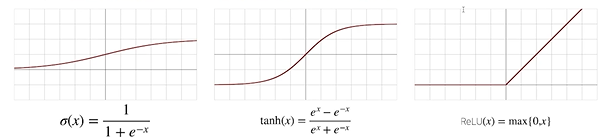
선형 모델과 활성함수를 반복적으로 사용하는 것이 오늘날의 대표적인 딥러닝 모델이다.
여러 층을 사용하는 이유
층이 깊을수록 목적함수를 근사하는데 필요한 뉴런의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능하다.
층이 얇으면(적으면) 필요한 뉴런의 숫자가 기하급수적으로 늘어나서 넓은 신경망이 되어야 한다.
하지만 층이 깊어지면 학습하기가 더 어려워짐! 나중에 CNN 공부할 때 자세히 공부.
여긴 더 공부해보자...📍증명해보고싶음
Softmax 함수
분류 문제를 풀 때 주로 사용하는 함수로,
모델의 출력을 확률 로 해석할 수 있게 변환해주는 연산이다.
순전파와 역전파
순전파
선형모델과 활성함수를 반복적으로 적용하는 과정.
역전파
경사하강법을 적용하여 parameter를 업데이트 하는 과정. (윗층부터 역순으로)
손실함수 L 사용.
역전파 알고리즘의 원리 - Chain Rule
