(1) 데이터의 표현

정보의 단위: bit

0과 1을 나타내는 가장 작은 정보 단위 📐
1bit는 0 또는 1, 두가지 정보를 표현할 수 있다.
∴ n비트는 2ⁿ가지 정보를 표현 할 수 있다.

💡 1byte == 8bit
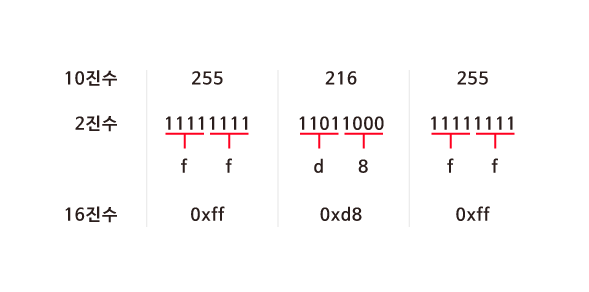
255 (10진수) = 1111 1111 (2진수) == 0xff (16진수)
4bit → 16진수 1문자

진법 변환

10진수	2진수	16진수
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

(ex) 1010(2) = 10(10) = A(16)

2진수: 0b1010 (b = binary)
10진수: 10
16진수: 0xA (x = hexadecimal)

Unsigned Integer

부호 없는 정수

모든 비트를 수의 크기를 나타내는 데 사용
범위: 0 ~ (2ⁿ - 1) (n = 비트 수)

(ex) 8비트라면 0~255 표현 가능

❓ 그렇다면 8비트 최대값인 255에서 1을 더하면?
1111 1111 + 0000 0001 = 0000 0000 (오버플로우)

Signed Integer

부호 있는 정수

• Sign-Magnitude 방식
  가장 왼쪽 비트(MSB, Most Significant Bit)를 부호 비트로 사용하고,
  나머지 비트는 크기를 나타낸다.

  +5 → 0000 0101
  -5 → 1000 0101

  👎🏻 단점
  +0과 -0이 따로 존재
  덧셈/뺄셈 등의 연산을 하려면 특별한 처리 로직이 필요

𝑟진법에서 정의되는 보수

𝑟진법에서 정의되는 보수는 𝑟 − 1의 보수와 진보수인 𝑟의 보수이다.

❓ 보수가 뭐야?

보수는 어떤 수를 더해서 특정 값을 만들기 위한 차이를 의미함
컴퓨터에서는 뺄셈을 덧셈으로 바꾸기 위해 보수를 사용

• r − 1의 보수
  각 자릿수를 r-1에서 뺀 수로 바꾼 것

  (ex) 10진법에서 (r=10)
  → 9의 보수 (r−1 = 9)
  652의 9의 보수는
  9-6=3, 9-5=4, 9-2=7 ⇒ 347

• r의 보수
  (r-1)의 보수에 1을 더한 것
  ∴ 진보수 = 감산보수 + 1

  (ex) 위에서 652의 9의 보수가 347이었으므로
  10의 보수는 347 + 1 = 348

2진수에서 보수는 1의 보수와 2의 보수가 있다.

1의 보수(1's complement)

음수를 나타낼 때, 양수의 모든 비트를 반전시킨다. (0 ↔ 1)
부호 비트도 함께 뒤집는다.

+5 = 0000 0101
→ -5 = 1111 1010 (모든 비트를 반전)

👎🏻 단점
여전히 +0 (0000 0000)과 -0 (1111 1111)이 존재
연산은 Sign-Magnitude보다 좀 더 편하지만, 여전히 복잡함

2의 보수(2's complement) : 가장 널리 사용

컴퓨터가 음수나 뺄셈을 편리하게 처리하기 위해 고안된 수 체계

음수 = 양수의 2의 보수 (mod 2n 관점)
2의 보수 = 1의 보수(비트를 반전) + 1

+5 = 0000 0101
-5 = 1111 1011 (1의 보수 1111 1010 + 1)

👍🏻 장점
음수와 양수를 같은 방식으로 더하고 빼기 가능
0은 오직 하나 (0000 0000)
덧셈/뺄셈 처리 시 carry로 자동 처리됨

💡 mod 2ⁿ
mod는 모듈로(Modulo) 연산으로, 어떤 수를 2ⁿ으로 나누었을 때의 나머지를 뜻한다.
n비트 시스템에서는 모든 연산이 2ⁿ을 기준으로 반복된다.
즉, 0부터 2ⁿ-1까지의 값만 사용 가능하고, 이 범위를 벗어나는 값은 2ⁿ으로 나눈 나머지(mod)만 사용한다.

두 정수 A와 B가 같은 나머지를 가지면 모듈러 합동 관계
→ A ≡ B (mod N)
A와 B를 N으로 나누었을 때 나머지가 같다는 뜻

💡 음수의 정의: 덧셈의 항등원
수학적으로 x + (-x) = 0 이 되어야 -x는 x의 음수이다.
컴퓨터는 감산(-)이 불편해서, 대신 덧셈만으로 모든 연산을 처리하려고 한다. 그래서 음수를 표현하기 위해 2의 보수를 사용한다.

x + (2ⁿ - x) = 2ⁿ ≡ 0 (mod 2ⁿ)
결국 음수 -x는 2ⁿ - x로 표현된다.

❓ 그럼 이게 2의 보수랑 어떻게 연결되는데?
음수는 양수를 2ⁿ에서 뺀 값으로 표현된다.

(ex) -1을 8비트로 표현하려면?
2⁸ = 256
256 - 1 = 255
255를 2진수로 표현하면? → 1111 1111
∴ -1 = 1111 1111 (2의 보수)

(ex) 8자리의 2진수 0100 1011 (10진수: 75)의 2의 보수는?
1 0000 0000 (256) - 100 1011 (75) = 1011 0101

p.s. 1 0000 0000을 8비트 연산에서 쓰면 overflow가 나서 0이 됨
→ 즉, 8비트에서는 256 = 0
∴ 0 - 75 = -75 (O), 256 - 75 = 181 (X)

💡 1의 보수를 이용하여 2의 보수 계산 가능

(ex) 0100 1011 (75)
→ (1의 보수 변환) 1011 0100
→ 1011 0100 + 1 = 1011 0101 (-75)

💡 2의 보수를 이용한 뺄셈
덧셈 회로만으로도 뺄셈과 음수 처리가 가능

(ex) 100 + (-75)
0110 0100 + 1011 0101 = 1 0001 1001

2의 보수에서 오버플로우가 발생

오버플로우(Overflow)

계산 결과가 표현할 수 있는 범위를 초과하면, 잘못된 결과가 나오는데, 이걸 오버플로우라고 한다.
특히 부호 있는 정수(Signed Integer) 연산에서 발생한다.

*Carry(자리 올림)와 다르다!

Carry	Overflow
무부호 연산에서 자릿수가 올라가는 현상 (덧셈 시)	부호 있는 연산에서 표현 범위를 넘는 오류

1️⃣ 덧셈에서 오버플로우 발생 조건

• 양수 + 양수 → 음수가 나올 때
  (ex) 127 + 1 → 128이 되어야 하지만 8비트에서는 표현 불가
  
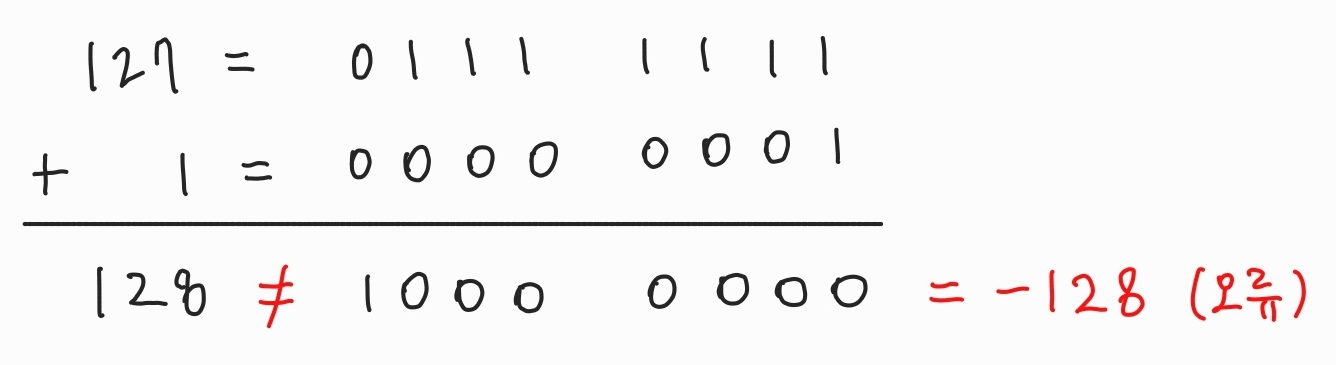
• 음수 + 음수 → 양수가 나올 때
  (ex) (-65) + (-70) → -135가 되어야 하지만 표현 불가
  

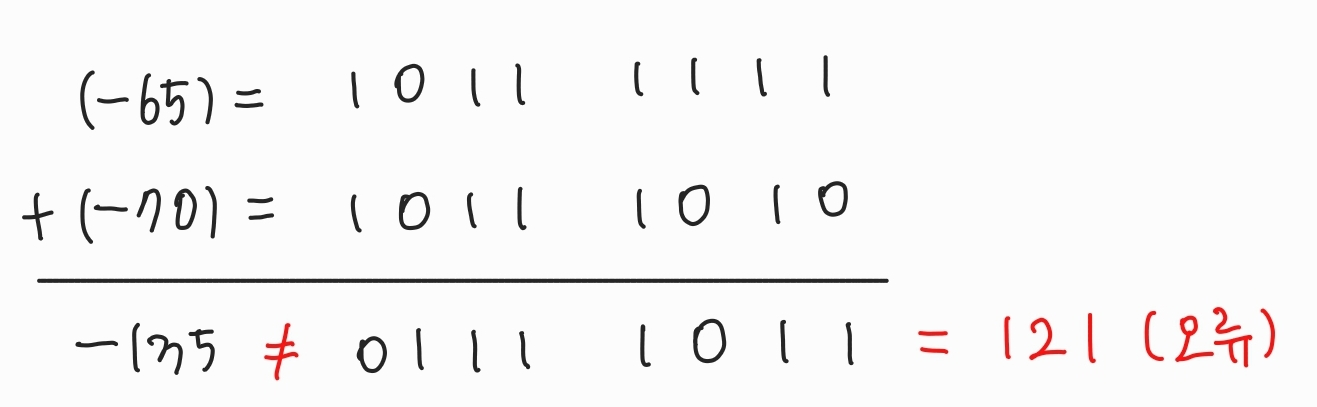
2️⃣ 뺄셈에서 오버플로우 발생 조건
뺄셈은 실제로 덧셈(A - B = A + (-B))으로 처리되므로,
"A + (-B)" 연산에서 오버플로우 발생 여부를 확인한다.

• 음수 - 양수
• 양수 - 음수

💡 오버플로우 검출 방법

• MSB(부호 비트)를 체크 (0 = 양수, 1 = 음수)
  덧셈 후 두 입력 값과 결과 값의 MSB가 다르면 오버플로우 발생
  MSB 자리에서의 자리올림(Carry) 여부로도 판단할 수 있음
  Carry_in ≠ Carry_out → 오버플로우 발생

• 연산 범위 초과 여부 확인
  부호 없는 정수 : 0 ~ 2ⁿ - 1
  부호 있는 정수 : −2ⁿ⁻¹ ~ 2ⁿ⁻¹ - 1
  (ex) 8비트 2의 보수에서는 -128 ~ 127의 범위를 초과하는지 확인

고정 소수점(Fixed-point)

실수를 표현할 때 정수부와 소수부의 비트(자릿수)가 미리 정해져 있다.

(ex) 16비트 중에서 정수부 8비트, 소수부 8비트로 나누어 사용한다면
정수부: -128 ~ 127 (부호가 있다면)
소수부: 2-1, 2-2, ⋯, 2-8

∴ 최대 정밀도(1/256)는 이미 결정되어 있으며, 범위와 정밀도가 고정되어 있다.

👍🏻 장점

• 연산이 단순해서 하드웨어 구현이 상대적으로 쉽다.
• 특정 응용(임베디드 등)에서 자릿수가 예측 가능하므로 오차 관리가 용이하다.

👎🏻 단점

• 표현 범위가 제한적이다. 소수부가 커지면 정수부가 작아지고, 정수부가 커지면 소수부가 줄어드는 트레이드오프가 크다.
• 아주 큰 수나 아주 작은 수 표현이 어렵다.

  ❓ 언더플로우

  컴퓨터는 0.000000000000000000000000000000123 같이, 표현할 수 있는 최소 값보다 작은 수를 0으로 처리함

(ex) 12.75를 고정소수점으로 표현

12 + 0.75 = 1100 + 0.11 = 1100.11

💡 소수 0.75를 2진수로 바꾸는 법
소수는 곱하기 2 해서 정수 부분만 따로 적어주는 방식으로 변환함

0.75 × 2 = 1.5 → 정수 부분: 1
0.5 × 2 = 1.0 → 정수 부분: 1
끝 (소수부가 0이 되면 멈춤)

∴ 0.75의 2진수 = 0.11

• 고정소수점 (16비트) 표현

만약 8비트 정수부 + 8비트 소수부 형식으로 저장한다고 가정하면,
정수부(8비트, 앞쪽 0으로 패딩) : 0000 1100
소수부(8비트, 뒤쪽 0으로 패딩) : 1100 0000
최종 고정소수점 표현 : 00001100.11000000

부동 소수점(Floating-point)

실수를 지수부(Exponent)와 가수부(Mantissa, Fraction)로 분리해 표현하는 방식이다.
일반적으로 2진수를 기반으로 부호(1bit) + 지수 + 가수 형태를 취한다.

• 지수(exponent)
  실제 지수가 아니라, 바이어스(Bias)가 적용된 값이 저장된다.

  (ex) 지수 비트가 10000011 (131)이라면
  → 실제 지수 = 131 - 127 = 4

IEEE 754 (전기 전자 기술자 협회(IEEE)에서 개발한 표준 부동소수점 방식이며 현재 컴퓨터에서 가장 널리 쓰이는 방식) 가 대표적인 부동소수점 표준이다.

• 단정도(Single Precision, 32bit)
  일반적으로 C언어 float

  4byte = sign(1bit) + exp(8bit) + mantissa(23bit)

  mantissa → 실제로는 숨겨진 1(hidden bit) 개념을 포함해, 실질적으로 24비트 정밀도

• 배정도(Double Precision, 64bit)
  일반적으로 C언어 double

🔗 -314.625를 부동소수점으로 변환해보자! (단정도)

부호부 → 가수부 → 지수부

1. 부호를 확인한다.
   음수니까 32비트의 맨 앞 자리는 1이 된다.

2. 숫자의 절댓값을 2진수로 표현한다.
   314.625 = 100111010.101

3. 이 2진수의 소수점을 왼쪽으로 이동시켜서 소수점 왼쪽에 1만 남도록 한다. 가수는 항상 1.XXXX 형태로 간주된다. (hidden 1)
   100111010.101 → 1.00111010101

4. 이제 이렇게 표현할 수 있다.
   **-314.625 = 1.00111010101 × 2⁸

5. 소수점의 오른쪽 부분 00111010101을 가수부 23비트의 앞에서부터 채운다. 남는 자리는 0으로 채운다.
   

6. 지수에 bias인 127을 더해준다.
   지수가 바이어스보다 클 경우 지수 - bias (예) 131-127=4
   8 + 127 = 135 = 1000 0111
   

   ❓ bias를 왜 써야 돼?

   부동소수점에서 지수는 음수도, 양수도 될 수 있다. 그런데 지수부는 2진수로만 표현해야 하니, 음수를 직접 표현할 수 없다.
   그래서 bias(편향) 값을 더해서 양수처럼 표현하는 방식이 사용된다.

   포맷	지수 비트 수	Bias 값
   단정도(float, 32비트)	8비트	127
   배정도(double, 64비트)	11비트	1023

   (참고) bias = 2ᵏ - 1 (k = 지수 비트 수)

7. 부동소수점 01000011 10011010 10100000 00000000를 16진수 0x439AA000로 변환한다.

👎🏻 부동소수점 계산 시 발생할 수 있는 문제점

• Rounding(반올림) 문제
  부동소수점 숫자는 한정된 비트로 표현되기 때문에, 어떤 숫자를 완전히 정확하게 표현할 수 없을 때가 많다. 특히 무한히 이어지는 2진 분수를 저장할 때 부정확성이 발생할 수 있다.
  (ex) 0.1 = 0.00011001100110011...(무한 반복)
float 타입으로 0.1을 표현하려고 하면 정확한 값이 저장되지 않고 근사값이 저장된다. 이로 인해 미세한 오차가 발생할 수 있다. 예를 들어 0.1을 반복해서 더하는 경우, 실제로는 9.9999999999처럼 근사치가 축적되어 최종적으로 오차가 발생할 수 있다.

• 오버플로우/언더플로우
  너무 큰 수 → 오버플로우 → Infinity
  너무 작은 수 → 언더플로우 → 0 혹은 Subnormal 형태로 표현