Amdahl’s Law
“전체 시스템에서 일부만 개선하면 전체 성능 향상에는 한계가 있다.”
➡️ 이것을 수식으로 표현한 것이 바로 암달의 법칙이다.
프로그램의 일부를 빠르게 만들었다고 해도, 나머지가 느리다면 전체 프로그램 속도는 그렇게 많이 향상되지 않을 것이다.
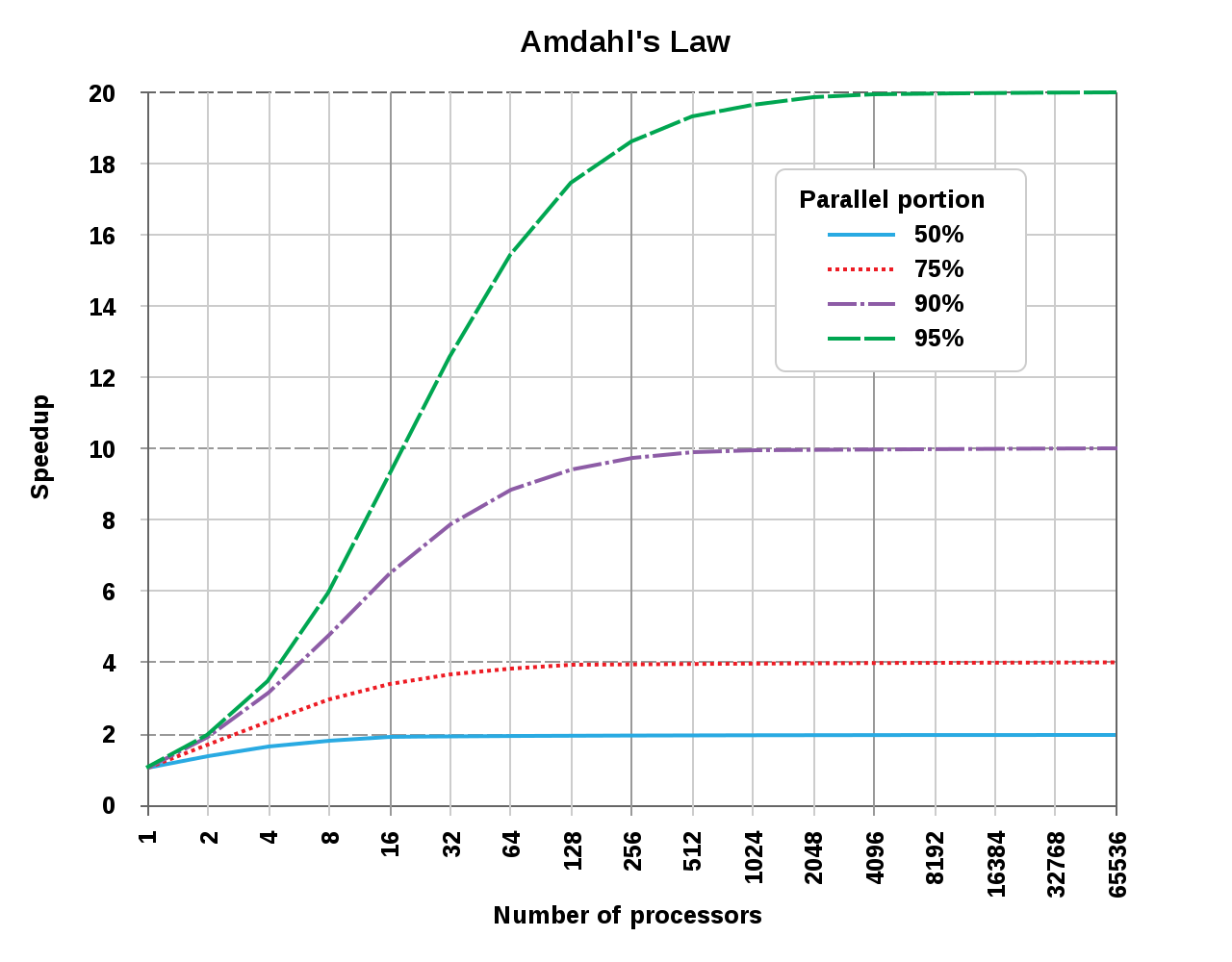
프로그램은 병렬 처리가 가능한 부분과 불가능한 순차적인 부분으로 구성되므로 프로세서를 아무리 병렬화 시켜도 더 이상 성능이 향상되지 않는 한계가 존재한다.
이 법칙은 성능 개선이 전체에 얼마나 영향을 줄 수 있는지를 계산할 때 사용된다.
"최적화를 통한 성능 향상 폭은?"
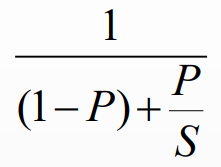
P = 최적화의 영향을 받는 실행 시간 비율 (개선 가능한(가속 가능한) 비율)
S = 속도 향상 배수 (그 부분을 얼마나 빠르게 만들 수 있는가)
Q. 만약 프로그램의 25%가 2배 빨라진다고 할 때, 속도 향상은?
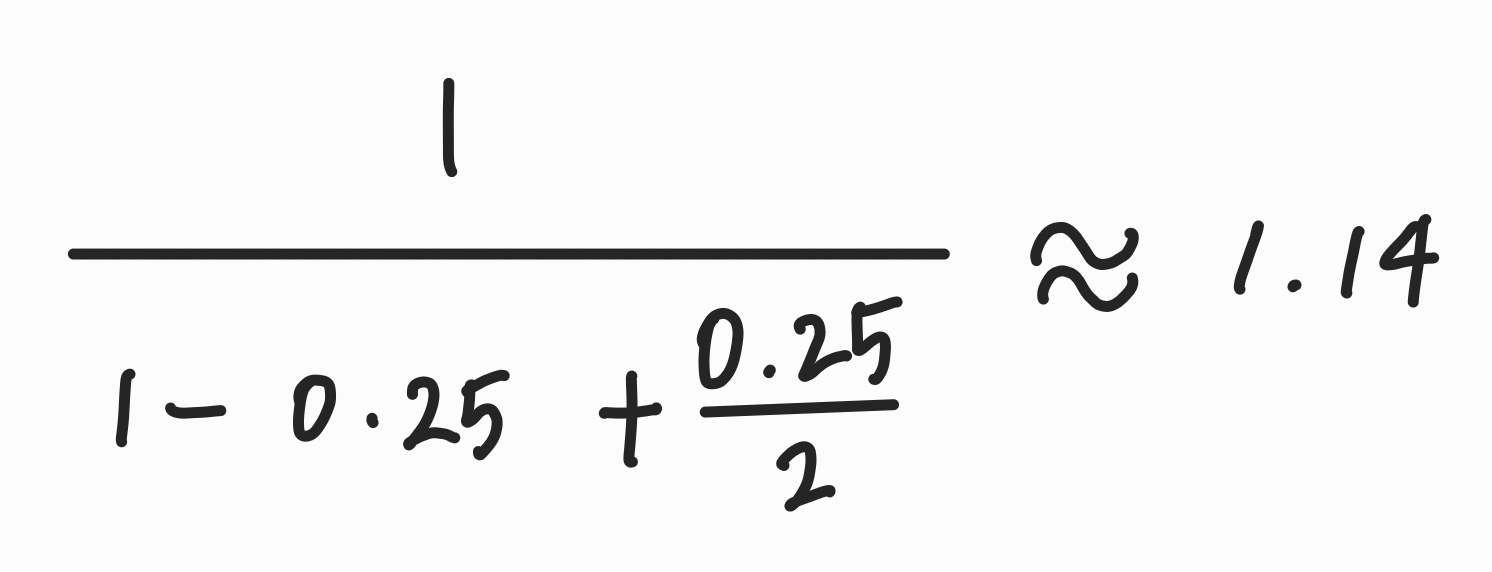
Q. 만약 프로그램의 25%가 무한대 빨라진다고 할 때, 속도 향상은?
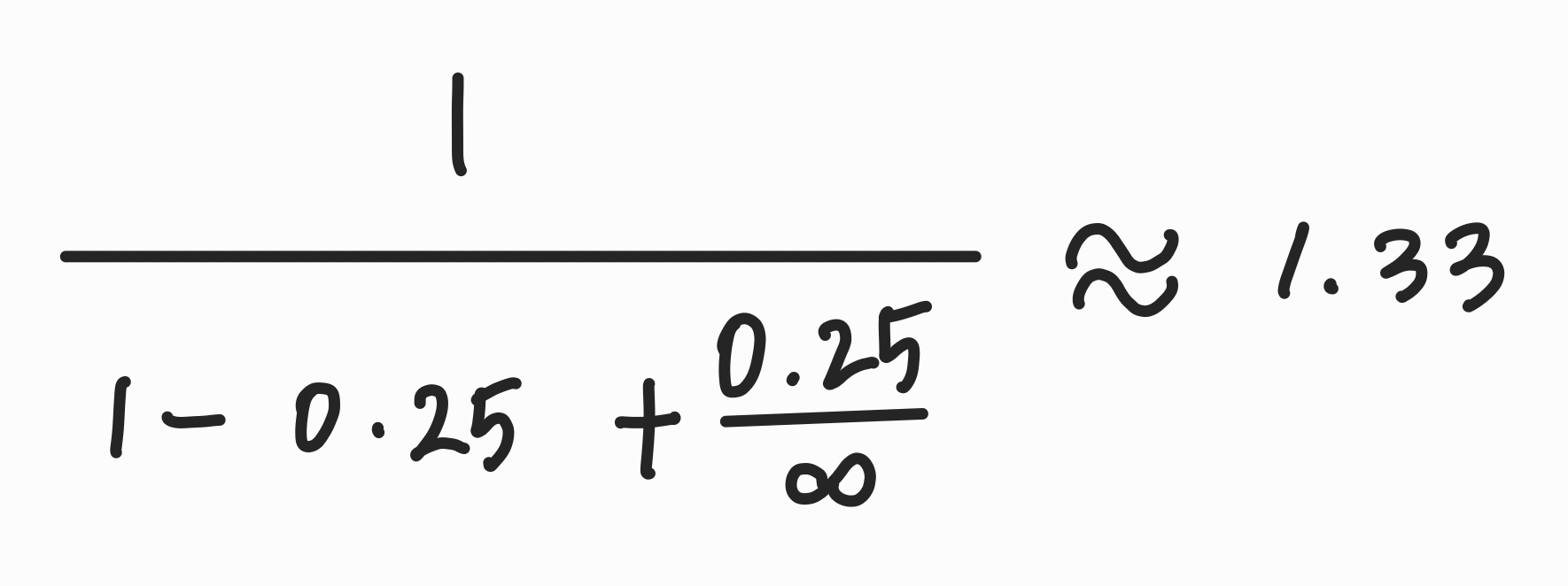
최대 약 1.33배에 불과
→ 프로그램의 75%는 여전히 원래 속도대로 실행되기 때문에, 속도 향상의 병목 지점이 되는 것
Amdahl’s Law for Parallelization
"병렬화가 성능을 얼마나 향상시킬 것인가?"
전체 프로그램 중 병렬화가 가능한 부분을 병렬로 처리할 경우, CPU 코어 수를 늘렸을 때 성능이 얼마나 향상되는지를 예측하는 법칙이다.
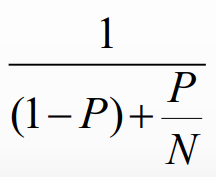
P = 병렬화 가능한 비율 (0 ≤ P ≤ 1)
N = 전체 쓰레드 (코어 수가 몇 개냐?)
Q. 10%가 시리얼(즉, 90% 병렬화 가능)일 때 최대 속도 향상은? (N = 2 or N = 무한대)
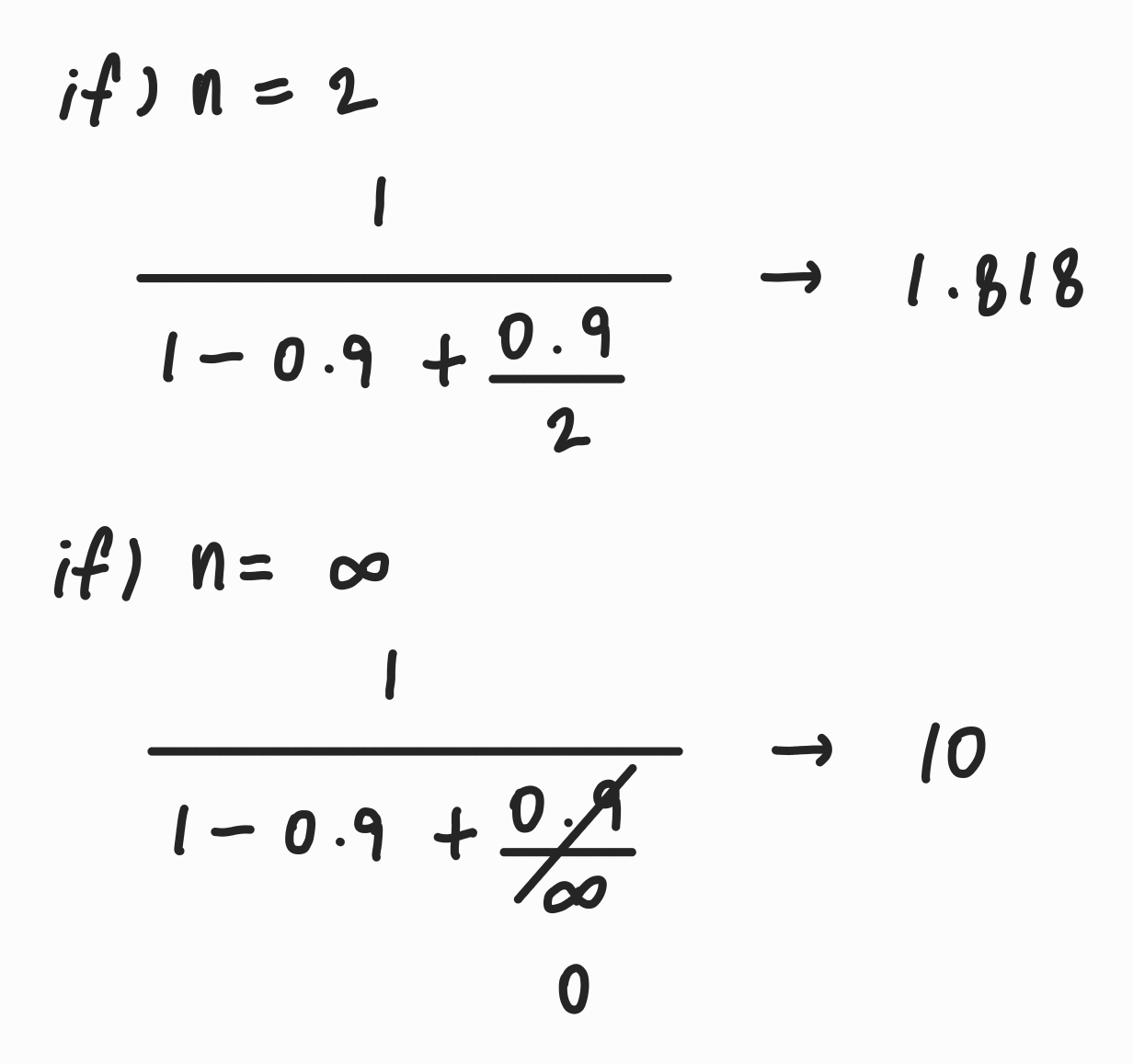
암달의 법칙은 대규모 멀티프로세서를 활용하기 위해 매우 병렬적인 코드를 요구한다.
암달의 법칙이 병렬 컴퓨팅의 한계를 설명하는 법칙이라면, 이를 극복하거나 효율적으로 활용하기 위한 두 가지 대표적인 접근 방식이 바로 ⬇️
-
Two approaches to Parallel Computing
-
강력한 스케일링 : 직렬 구성 요소 축소
👍🏻 같은 문제 크기로 더 짧은 시간에 문제를 푸는 전략
👎🏻 병렬화 난이도 증가
(ex) 1GB 이미지 처리 → 1초 안에 처리하려고 CPU 4개, 8개로 나눠 처리 -
약한 스케일링 : 문제 크기 증가
👍🏻 처리 시간을 고정한 상태에서 문제 크기를 늘리는 전략
👎🏻 모든 문제에 적용 불가 (문제 크기를 키울 수 있어야 함)
(ex) 1GB 이미지 1초 → CPU 2개면 2GB 이미지, 4개면 4GB 이미지 처리
-
