(5) 불 대수

탱구리·2025년 4월 21일

Computer System

목록 보기
5/10

1. 기본 법칙

교환 법칙

A⋅B=B⋅AA \cdot B = B \cdot A
A+B=B+AA + B = B + A

결합 법칙

A⋅(B⋅C)=(A⋅B)⋅CA \cdot (B \cdot C) = (A \cdot B) \cdot C
(A+B)+C=A+(B+C)(A + B) + C = A + (B + C)

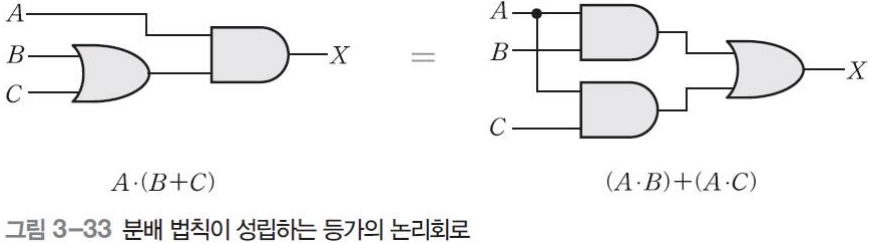
분배 법칙

A⋅(B+C)=(A⋅B)+(A⋅C)A \cdot (B + C) = (A \cdot B) + (A \cdot C)

다중 부정

Aˉˉ=A\bar{\bar{A}} = A

논리 부정을 두 번 연속으로 수행하면 원래의 자신이 된다.

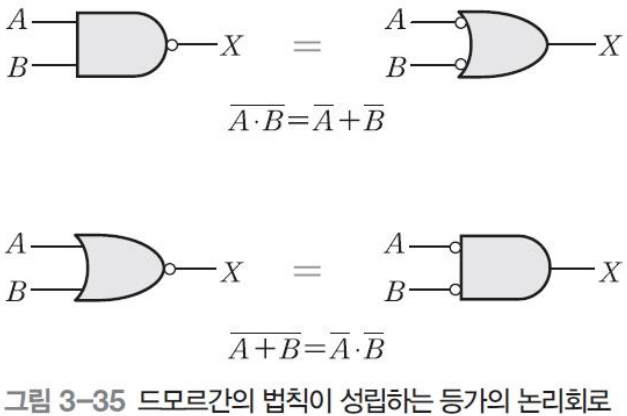
드모르간의 법칙

A⋅B‾=Aˉ+Bˉ\overline{A \cdot B} = \bar{A} + \bar{B}
A+B‾=Aˉ⋅Bˉ\overline{A + B} = \bar{A} \cdot \bar{B}

not (A or B) = (not A) and (not B)
not (A and B) =(not A) or (not B)

X1+X2+⋯+Xn‾=X1ˉX2ˉ⋯Xnˉ\overline{X_{1} + X_{2} + \cdots + X_{n}} = \bar{X_{1}}\bar{X_{2}}\cdots\bar{X_{n}}
X1X2⋯Xn‾=X1ˉ+X2ˉ+⋯+Xnˉ\overline{X_{1}X_{2}\cdots X_{n}} = \bar{X_{1}} + \bar{X_{2}} + \cdots + \bar{X_{n}}

2. 기본 정리

A+0=AA + 0 = A
A+1=1A + 1 = 1
A⋅0=0A \cdot 0 = 0
A⋅1=AA \cdot 1 = A
A+A=AA + A = A
A+Aˉ=1A + \bar{A} = 1
A⋅A=AA \cdot A = A
A⋅Aˉ=0A \cdot \bar{A} = 0
AAAˉ\bar{A}A⋅AˉA \cdot \bar{A}
010·1=0
101·0=0
A+A⋅B=A⋅(1+B)=A⋅1=AA + A \cdot B \newline = A \cdot (1 + B) \newline = A \cdot 1 \newline = A
A+Aˉ⋅B=(A+A⋅B)+Aˉ⋅B=(A⋅A)+(A⋅B)+Aˉ⋅B=A⋅A+A⋅B+A⋅Aˉ+Aˉ⋅B=(A+Aˉ)⋅(A+B)=1⋅(A+B)=A+BA + \bar{A} \cdot B \newline = (A + A\cdot B) + \bar{A} \cdot B \newline = (A \cdot A) + (A \cdot B) + \bar{A} \cdot B \newline = A \cdot A + A \cdot B + A \cdot \bar{A} + \bar{A} \cdot B \newline = (A + \bar{A}) \cdot (A + B) \newline = 1 \cdot (A + B) \newline = A + B
(A⋅B)⋅(A+C)=A⋅A+A⋅C+A⋅B+B⋅C=A+A⋅C+A⋅B+B⋅C=A⋅(1+C)+A⋅B+B⋅C=A⋅1+A⋅B+B⋅C=A⋅(1+B)+B⋅C=A⋅1+B⋅C=A+B⋅C(A \cdot B) \cdot (A + C) \newline = A \cdot A + A \cdot C + A \cdot B + B \cdot C \newline = A + A \cdot C + A \cdot B + B \cdot C \newline = A \cdot (1 + C) + A \cdot B + B \cdot C \newline = A \cdot 1 + A \cdot B + B \cdot C \newline = A \cdot (1 + B) + B \cdot C \newline = A \cdot 1 + B \cdot C \newline = A + B \cdot C

3. 불 대수의 표준형

최소항과 최대항

profile
탱구리
이전 포스트

(4) 논리 게이트

다음 포스트

(6) 운영체제(OS)

0개의 댓글