[백준] 1309번 동물원 in Java

📜 문제

문제 링크

💡 2차원 풀이

dynamic programming으로 풀었고, dp table을
dp[i][0]을 세로 기준 1번째 칸부터 i번째 칸까지 고려했을 때 i번째 칸에 사자가 0마리인 경우,
dp[i][1]을 세로 기준 1번째 칸부터 i번째 칸까지 고려했을 때 i번째 칸에 사자가 1마리인 경우로 정의했다.

1. 우선 dp[i][0]에 대해 설명하면,
   현재 칸을 세로 기준 i번째 칸이라고 했을 때 현재 칸에 사자가 0마리라는 것은 이전 칸(i-1)은 어떤 상태여도 상관없다. 즉, (i-1)번째 칸에는 사자가 1마리가 있든, 0마리가 있든 상관 없다는 것이다. 이를 식으로 표현하면 다음과 같다.

dp[i][0] = dp[i-1][0] + dp[i-1][1]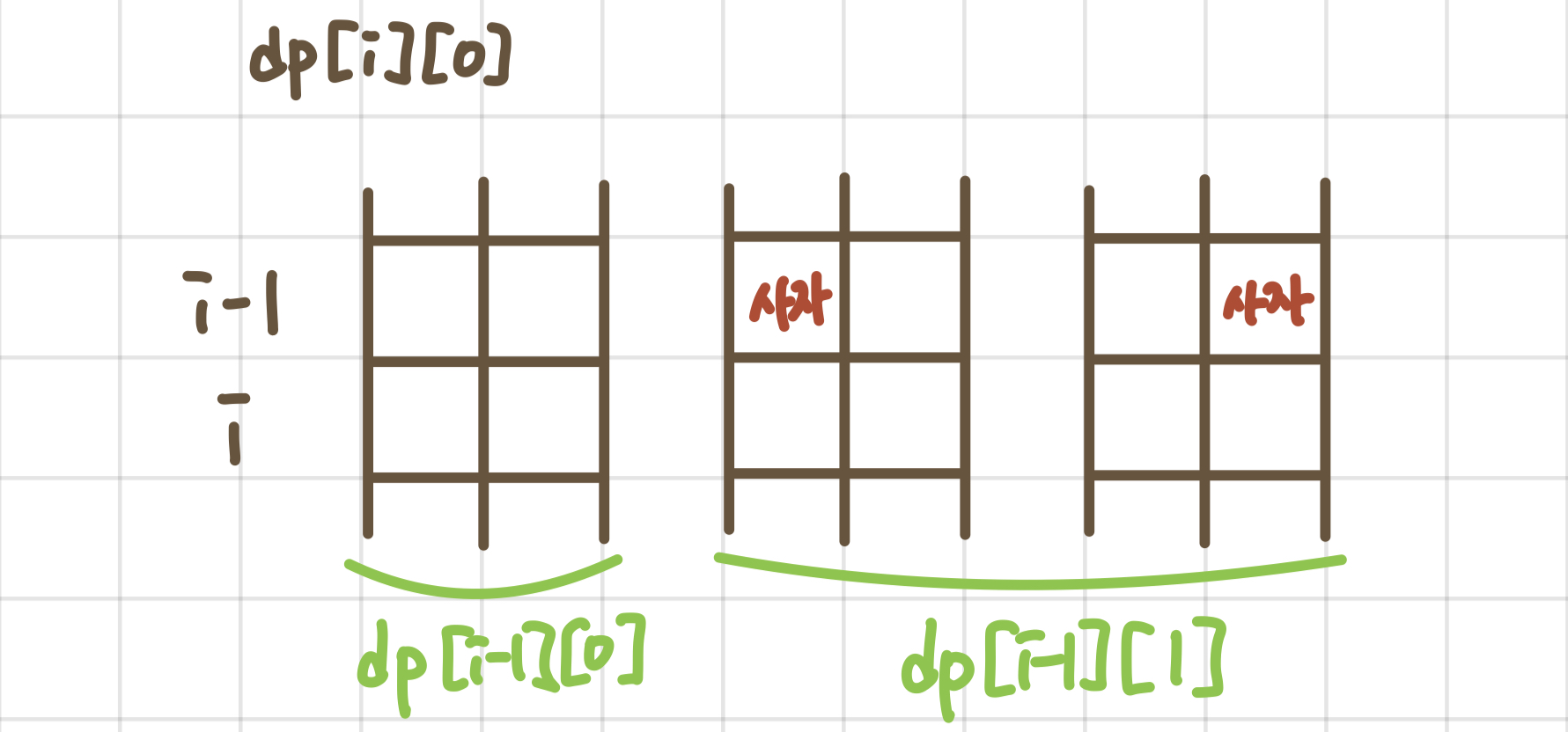

2. 다음으로 dp[i][1]은,
   이전 칸에는 사자가 없다면 현재칸에는 사자가 왼쪽에 들어가든 오른쪽에 들어가든 상관이 없다. 따라서 이전 칸에 사자가 없다면 현재 칸에 사자가 들어갈 수 있는 경우의 수가 두가지이다.
   이전 칸에 사자가 한마리 있다면, 현재 칸에 들어갈 수 있는 사자의 위치는 정해진다. 이를 식으로 나타내면 다음과 같다.

dp[i][1] = 2 * dp[i-1][0] + dp[i-1][1]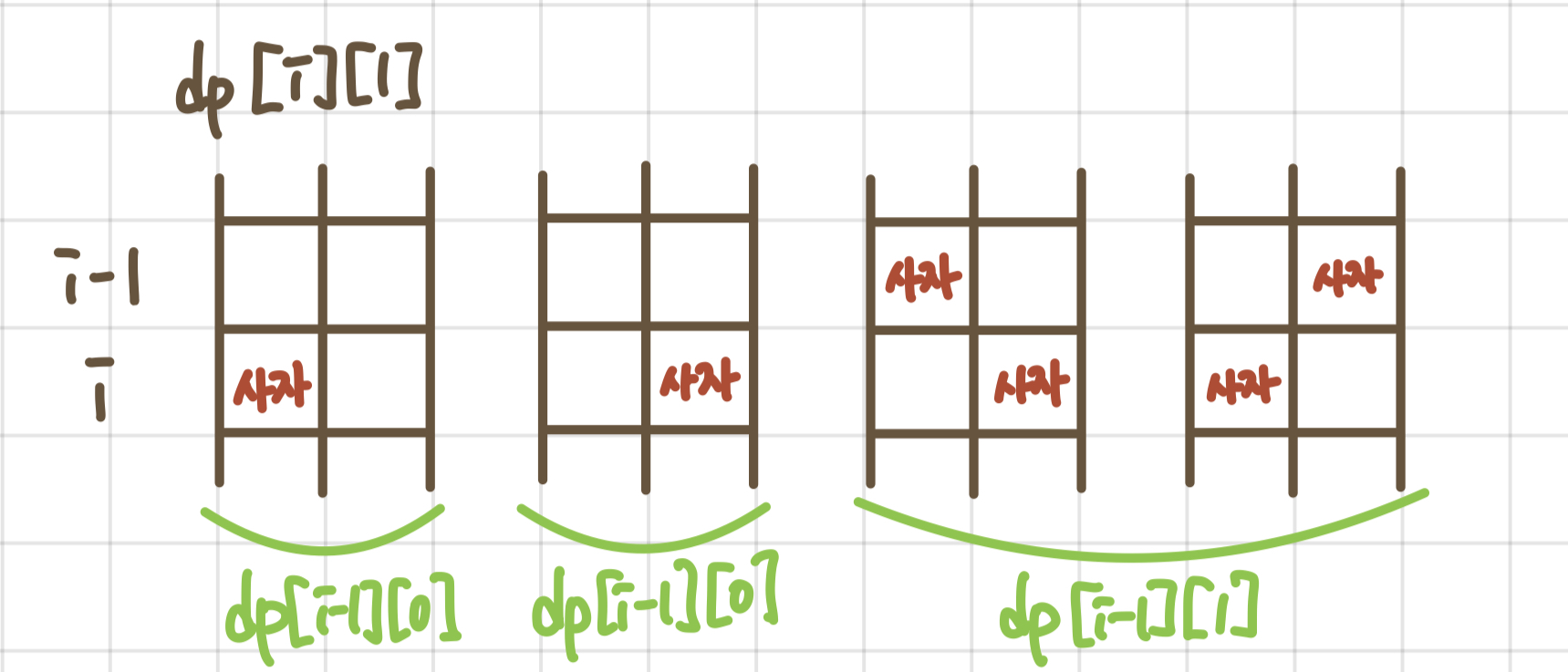

그런데 우리가 구하고자 하는 것은 N번째 칸까지 고려했을 때 사자를 배치하는 경우의 수를 구하는 것이기 때문에 dp[n][0] + dp[n][1]이 정답이 된다.

⌨️ 2차원 코드

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());

// dp[i][0]: 세로 i칸에 사자가 0마리인 경우, dp[i][1]: 세로 i칸에 사자가 1마리인 경우
int[][] dp = new int[n + 1][2]; 
dp[1][0] = 1; dp[1][1] = 2;

for (int i = 2; i <= n; i++) {
    dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % 9901;
    dp[i][1] = (dp[i - 1][1] + 2 * dp[i - 1][0]) % 9901;
}

System.out.print((dp[n][0] + dp[n][1]) % 9901);

💡 1차원 풀이

dp table을
d[i]를 세로 기준 1번째 칸부터 i번째 칸까지 고려했을 때 사자를 배치하는 경우의 수로 둔다.

1. i번째 칸에 사자를 배치하지 않는 경우를 생각해보면 2차원 배열로 풀었을 때의 dp[i][0]와 같이, (i-1)번째 칸은 어떤 상태여도 상관 없다. 즉 dp[i-1]의 경우의 수가 생긴다.

2. i번째 칸에 사자를 배치하는 경우를 생각해보자.
   - (i-1)번째 칸에 사자가 한마리도 없는 경우에는 사자를 왼쪽 또는 오른쪽에 둘 수 있다는 2가지의 경우의 수가 생긴다.
   이때 1.에 의해 (i-1)번째 칸에 사자를 배치하지 않는 경우의 수는 dp[i-2]로 나타낼 수 있다. 따라서 2 * dp[i-2]로 표현할 수 있다.
   - (i-1)번째 칸에 사자가 한마리 배치된 경우 에는 i번째 칸에 들어가는 사자의 위치가 자동으로 정해진다.
   이때 (i-1)번째 칸에 사자가 한마리 배치된 경우를 표현하려면 여집합의 성질을 이용해서 (i-1)번째 칸까지 고려했을 때 사자를 배치하는 경우의 수에서 (i-1)번째 칸에 사자가 없는 경우의 수를 빼면 된다.
   즉, dp[i-1] - dp[i-2]로 표현할 수 있다.

1.과 2.의 경우의 수를 합치면, dp[i] = dp[i-1] + 2 * dp[i-2] + dp[i-1] - dp[i-2]가 되고, 최종적으로 dp[i] = 2 * dp[i-1] + dp[i-2]로 표현할 수 있다.

⌨️ 1차원 코드

public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    int n = Integer.parseInt(br.readLine());

    int[] dp = new int[n + 1];
    dp[0] = 1; dp[1] = 3;

    for (int i = 2; i <= n; i++) {
        dp[i] = (2 * dp[i - 1] + dp[i - 2])  % 9901;
    }

    System.out.print(dp[n] % 9901);
}

😄 느낀 점

나는 2차원 배열로 dp 테이블을 만들어서 풀었는데, 다른 사람의 풀이를 보니까 1차원 배열로도 풀 수 있는 걸 보고 깜짝 놀랐다😲
문제를 풀 당시 2차원 배열로 풀면서도 식이 반복되는 게 보여서 1차원으로 줄일 수 있을까 엄청 고민했는데 끝끝내 찾지 못했었던 거라서 아쉽지만 이제라도 알았으니 괜찮아~
그나저나 dp는 실버문제도 점화식 세우는 게 아직 어려워서 오래 걸린다😅