[프로그래머스] 파괴되지 않은 건물 in Kotlin

📜 문제

문제 링크

💡 나의 풀이

2차원 배열을 1차원 배열로 나누어서, 1차원 배열의 누적합을 이용한 풀이이다.

예를 들어, 문제에서 주어진 board의 크기는 4 * 5이고, 현재 skill이 [1, 0, 1, 2, 3, 5]라고 하자.

이때 board에 있는 건물들의 내구도 변화량을 그림으로 나타내면 다음과 같다.

이 그림처럼 모든 skill 마다 내구도 변화를 board에 바로 반영시키도록 구현한다면, 시간복잡도가 어마무시해진다. (skill 횟수를 k라고 했을 때, O(knm)이 되어버린다.)

1. 먼저, 이 그림에서 행을 떼어서 1차원 배열로 봤을 때 문제를 푸는 방법을 설명해보려고 한다.

이 배열을 "누적합의 결과를 담은 배열"로 보면,

"누적합 하기 전 배열"은 바로 다음 사진과 같다.

그렇다면! 예제에서 주어진 skill의 범위의 모든 행에 대해 "누적합 하기 전 배열"을 만들어 보면, 다음 이미지와 같아진다.

이렇게 풀 경우 매 행마다 c1열과 (c2 + 1)열에 알맞는 숫자를 넣어주기만 하면 되기 때문에, 시간 복잡도가 O(kn)으로 줄어든다.
하지만 아직 아쉽다! k의 최댓값은 250000이고, n의 최댓값은 1000이기 때문에 1초 안에 문제를 해결하기에 간당간당하다. 좀 더 줄여보자!

2. 1.에 이어서 열을 떼서 만든 1차원 배열로 똑같이 누적합 방식을 적용해보자.

1.과 똑같은 방식이니까 간단하게 하나의 이미지로 나타내보면 다음과 같다.

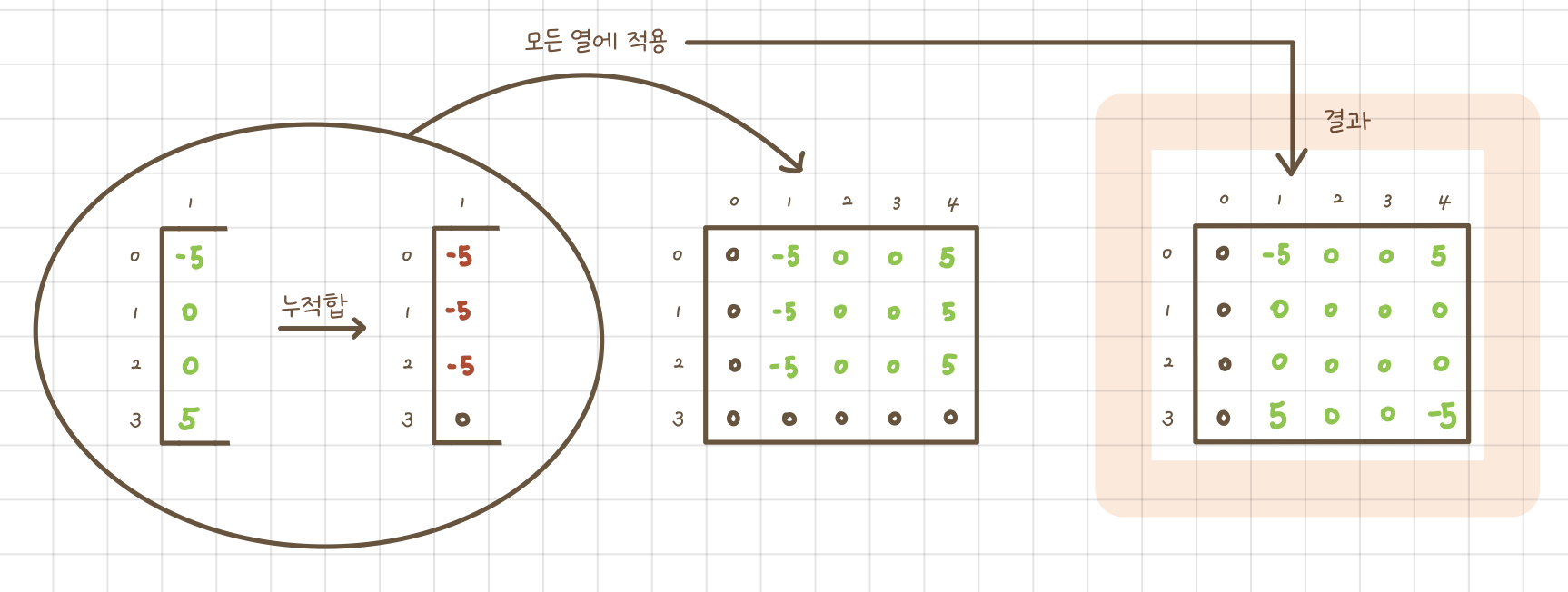
이 과정까지 마치면, 모든 skill에 대해 내구도 변화량을 표시하는데 4번의 연산만이 필요하기 때문에 시간 복잡도가 O(k)로 줄어든다.
아! 물론 정답을 내려면 skill을 모두 순회한 뒤에 이 내구도 변화량을 board에 반영하는 데에 O(nm)의 시간이 더 필요하기 때문에, 최종적으로 O(k + nm)의 시간복잡도로 문제를 해결하게 된다.

⌨️ 코드

class Solution {
    
    fun solution(board: Array<IntArray>, skills: Array<IntArray>): Int {
        var answer: Int = 0
        val n = board.size
        val m = board[0].size
        val degreeGraph = Array(n) {
            IntArray(m)
        }
        
        skills.forEach { skill ->
            val type = skill[0]
            val r1 = skill[1]; val c1 = skill[2]
            val r2 = skill[3]; val c2 = skill[4]
            val degree = skill[5]
            val d = if (type == 1) -1 * degree else degree
            
            degreeGraph[r1][c1] += d
            if (r2 + 1 in 0 until n) degreeGraph[r2 + 1][c1] -= d
            if (c2 + 1 in 0 until m) degreeGraph[r1][c2 + 1] -= d
            if (r2 + 1 in 0 until n && c2 + 1 in 0 until m) degreeGraph[r2 + 1][c2 + 1] += d
        }
        
        // 누적합 구하기 (행)
        for (r in 0 until n) {
            for (c in 1 until m) {
                degreeGraph[r][c] += degreeGraph[r][c - 1]
            }
        }
        // 누적합 구하기 (열)
        for (c in 0 until m) {
            for (r in 1 until n) {
                degreeGraph[r][c] += degreeGraph[r - 1][c]
            }
        }
        
        // 변경된 내구도 board에 반영하기
        for (r in 0 until n) {
            for (c in 0 until m) {
                board[r][c] += degreeGraph[r][c]
                if (1 <= board[r][c]) answer++ // 파괴되지 않은 건물 개수 세기
            }
        }
        
        return answer
    }
}

😄 느낀 점

1차원 배열의 누적합 문제만 풀어봤는데, 이번 기회에 2차원 배열의 누적합을 배울 수 있었다.
공부하면서 이 풀이방법은 꼭 기억하고 싶었기 때문에 오랜만에 블로그를 작성해봤다! 매우 뿌듯하다!😚