개요
스택과 큐는 프로그래밍이라는 개념이 탄생할 때부터 사용된 가장 고전적인 자료구조라고 한다.
간단히 두 자료구조를 설명하자면 스택은 후입선출 (늦게 들어간 놈이 먼저 꺼내짐) 큐는 선입선출 (먼저 들어간 놈이 먼저 꺼내짐)의 구조를 갖는다.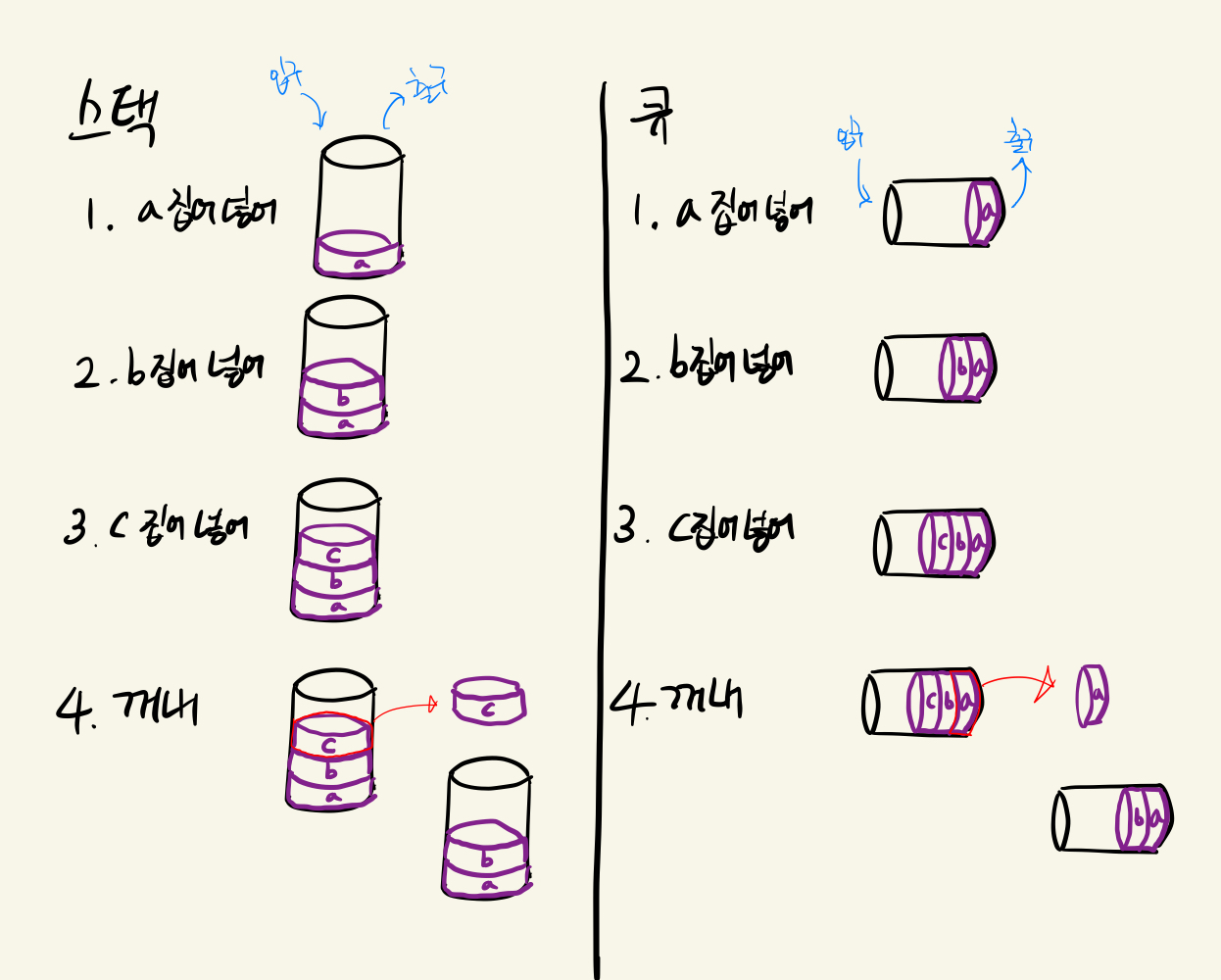
컴퓨터 운영체제나 네트워크 서버 등 다양한 환경에서 스택과 큐는 필수적인 자료구조라고 할 수 있다.
각 자료구조에 대해 좀 더 자세히 살펴보자.
스택
스택은 들어온 순서대로 쌓이게 되며, 꺼내서 쓸 때에는 가장 위에있는 것 (즉 가장 늦게 들어온 것)이 먼저 꺼내지게 된다. 이는 파이썬 built-in list 타입을 활용하여 쉽게 구현할 수 있는데, 파이썬 자체적으로 list의 가장 마지막에 새로운 원소를 추가하는 append, list의 가장 마지막 원소를 꺼내오는 pop 두 가지 메서드를 기본적으로 제공하기 때문이다.
큐
큐는 들어온 순서대로 쌓이지만, 꺼내서 쓸 때에는 가장 먼저 들어온 것이 먼저 꺼내지게 된다. 이 역시 built-in list 타입을 활용하여 구현할 수 있지만, 시간복잡도 측면에서 비효율성을 보일 수 있다.
큐에서 원소를 꺼내오는 연산을 deQueue라고 하는데, 만약 list에서 이 deQueue연산을 할 경우 O(n)의 시간 복잡도를 갖기 때문이다. 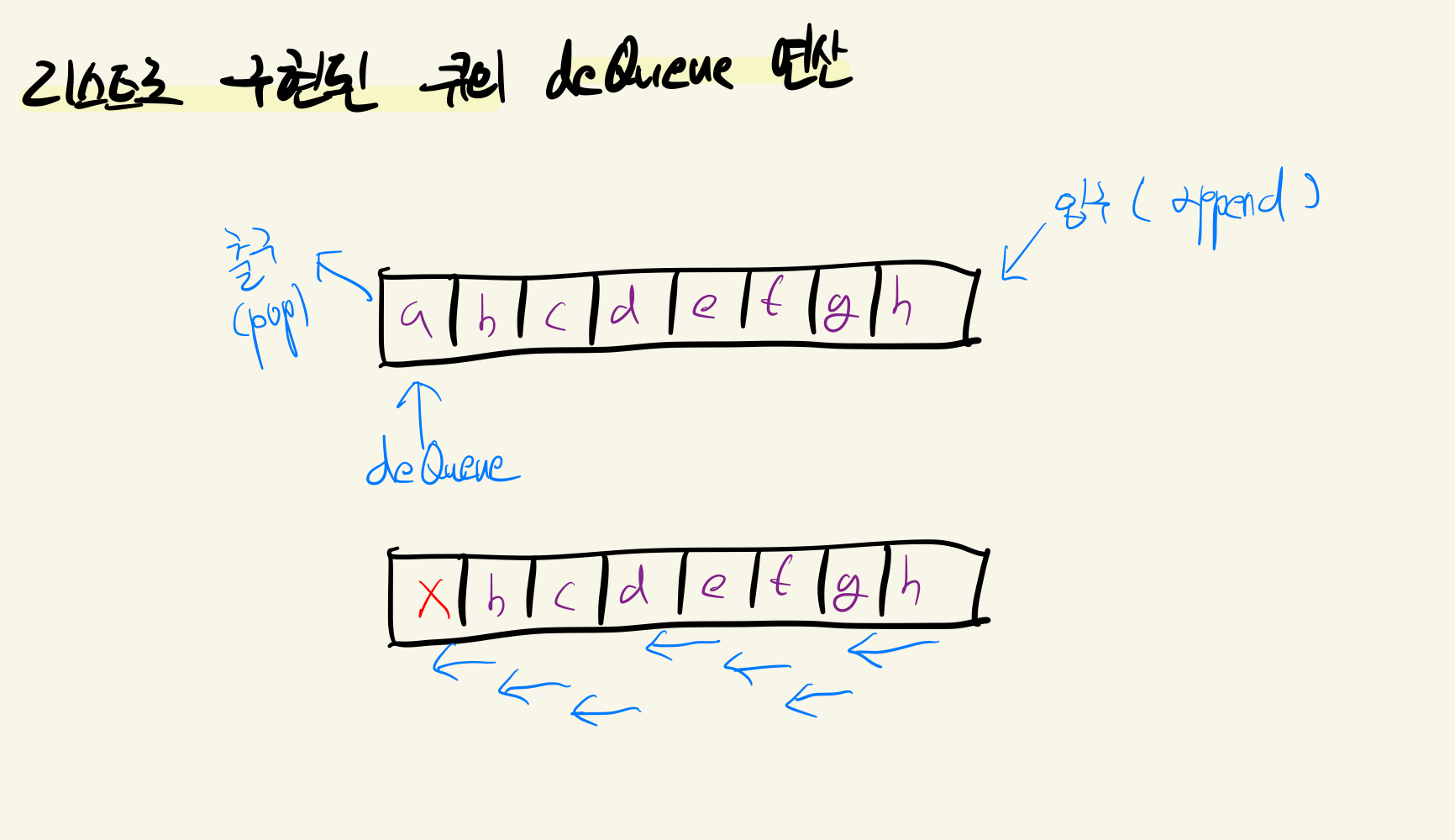 위의 사진에서 볼 수 있든 list로 구현된 큐의 경우, deQueue시
위의 사진에서 볼 수 있든 list로 구현된 큐의 경우, deQueue시 pop 메서드를 pop(0) 처럼 첫번째 인덱스를 꺼내오도록 구현해야 한다. 이렇게 될 경우 0번 인덱스가 비기 때문에 1번 ~ 마지막 까지의 인덱스에 위치한 원소들을 앞으로 한 칸 씩 땡겨와야 하는데, 이는 결국 모든 원소를 한번씩 방문해야 하는 연산이기 때문이다.
따라서 양 쪽 끝에서의 연산이 자유로은 "양방향 연결 리스트 (Doubly Linked List)"를 활용하여 큐를 구현하는 것이 효율성 측면에서 훨씬 효율적이라고 할 수 있다.
스택과 큐의 활용
스택과 큐가 어떤 상황에서 활용될 수 있는지 살펴보자.
스택
알고리즘 측면에서 스택은 다음과 같은 문제를 해결할 때 사용할 수 있다.
- 후위 계산법 수식 변경 및 문제 풀이
- 문자열 역순 출력 (
reverse()메서드가 더 효율적임) - 수식의 괄호 검사
또한 소프트웨어 개발의 다음과 같은 기능을 구현하는데 사용할 수 있다.
- 되돌리기 (일의 순서대로 스택에 쌓아두어 최근에 한 행동부터 하나하나 되돌릴 수 있다.)
큐
가장 대표적인 큐의 활용처는 생산자-소비자 패턴에서의 비동기적 작업 처리를 위한 태스크 파이프라인을 구축할 때를 들 수 있다. 파이썬의 대표적은 태스크 큐 라이브러리 celery 같은 것을 생각하면 이해가 쉽다.
한쪽에서 비동기적으로 해야할 일을 생산 하여 큐에 등록하고,
다른 한쪽에서는 비동기적으로 이러한 작업 목록을 가져와 소비(=작업) 한다.
웹 서비스에서 수 만명의 회원들에게 메일을 보낸다거나 하는 작업을 생각 예로 들 수 있다.
그 외에도 프린트 소프트웨어의 대기열 등에서 큐를 활용할 수 있을 것이다.
알고리즘 문제 풀이 측면에서는 큐를 통해 직접 문제를 해결하기보다는 큐를 기반으로 하는 문제풀이 기법들이 많은데, 너비 우선 탐색 (BFS)를 구현하는 등 의 상황에서 큐가 활용될 수 있다.
구현
스택
class Stack:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def is_empty(self):
return self.size() == 0
def push(self, item):
self.data.append(item)
def pop(self):
return self.data.pop()
def peek(self):
return self.data[-1]
큐
class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.node_count = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
def get_length(self):
return self.node_count
def traverse(self):
result = []
curr = self.head
while curr.next.next:
curr = curr.next
result.append(curr.data)
return result
def reverse(self):
result = []
curr = self.tail
while curr.prev.prev:
curr = curr.prev
result.append(curr.data)
return result
def get_at(self, pos):
if pos < 0 or pos > self.node_count:
return None
if pos > self.node_count // 2:
i = 0
curr = self.tail
while i < self.node_count - pos + 1:
curr = curr.prev
i += 1
else:
i = 0
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def __insert_after(self, prev, new_node):
next = prev.next
new_node.prev = prev
new_node.next = next
prev.next = new_node
next.prev = new_node
self.node_count += 1
return True
def insert_at(self, pos, new_node):
if pos < 1 or pos > self.node_count + 1:
return False
prev = self.get_at(pos - 1)
return self.__insert_after(prev, new_node)
def __pop_after(self, prev):
curr = prev.next
next = curr.next
prev.next = next
next.prev = prev
self.node_count -= 1
return curr.data
def pop_at(self, pos):
if pos < 1 or pos > self.node_count:
raise IndexError('Index out of range')
prev = self.get_at(pos - 1)
return self.__pop_after(prev)
class LinkedListQueue:
def __init__(self):
self.data = DoublyLinkedList()
def size(self):
return self.data.get_length()
def is_empty(self):
return self.size() == 0
def enqueue(self, item):
node = Node(item)
self.data.insert_at(self.size()+1, node)
def dequeue(self):
return self.data.pop_at(1)
def peek(self):
return self.data.get_at(1).data
기타
순환 큐
정해진 갯수의 저장공간을 갖는 큐이다. 큐의 입구 위치(rear)와 출구 위치(front)를 가리키는 포인터를 통해서 정해진 길이 내에서 원소들이 유연하게 입출력될 수 있다. 따라서 오버플로우가 발생하더라도, 큐의 길이에 원소가 가득 차있는게 아니라면 rear 포인터의 위치만 변화시킴으로 간단하게 대처할 수 있는 장점이 있다.
사전에 인덱스 길이를 정해두고 구현해야 하기 때문에 built-in list를 통해 구현해도 무방하다. 어차피 모든 인덱스가 이미 확보되어 있기 때문에 deQueue 연산후 원소들을 한칸 앞으로 땡길 필요가 없기 때문이다.
class CircularQueue:
def __init__(self, n):
self.max_count = n
self.data = [None] * n
self.count = 0
self.front = -1
self.rear = -1
def size(self):
return self.count
def isEmpty(self):
return self.count == 0
def isFull(self):
return self.count == self.max_count
def enqueue(self, x):
if self.is_full():
raise IndexError('Queue full')
self.rear = (self.rear + 1) % 3
self.data[self.rear] = x
self.count += 1
def dequeue(self):
if self.is_empty():
raise IndexError('Queue empty')
self.front = (self.front + 1) % 3
x = self.data[self.front]
self.count -= 1
return x
def peek(self):
if self.is_empty():
raise IndexError('Queue empty')
return self.data[(self.front + 1) % 3]
