GD / SGD

Gradient Descent

: 경사하강법

손실을 줄이는 알고리즘 !

미분값(기울기)이 최소 가 되는 점을 찾아 알맞은 weight(가중치 매개변수)를 찾아낸다.

1. w1에 대한 시작점을 선택

linear regression의 경우 매끈한 모양으로 시작점은 별로 중요하지 않다. ( 매끈한 모양이 아니라면, 시작점을 찾는 것은 중요 ! )
보통은 w1을 0으로 설정하거나, 임의의 값을 선택한다.

2. 시작점에서 손실 곡선의 기울기(Gradient)를 계산

3. 기울기의 보폭(Learning rate)를 통해 손실 곡선의 다음 지점으로 이동

4. 위의 과정을 반복해 최소값에 점점 접근

SGD (Stochastic Gardient Descent)

배치 크기가 1 인 경사하강법 알고리즘
= data set에서 무작위로 균일하게 선택한 하나의 예 에 의존하여 각 단계의 예측경사를 계산하는 방법

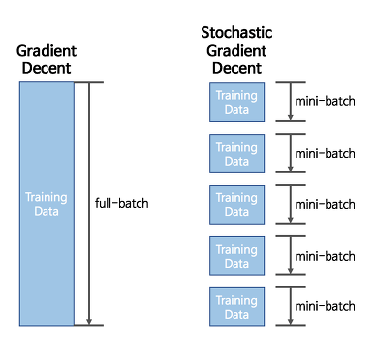
GD가 모든 데이터에 대한 손실함수를 구하고, 기울기를 구하는 과정이라면, SGD는 데이터를 mini-batch 단위 만큼 무작위로 추출하여 이 데이터만으로 학습을 하는 것 !

• 배치란 ?
  경사하강법에서 배치란 단일반복에서 기울기를 계산하는데 사용하는 data의 총 개수
  ( Gradient Descent 에서의 배치는 전체 데이터셋이라고 가정)

SGD 의 문제점

1. 비등방성 함수 문제

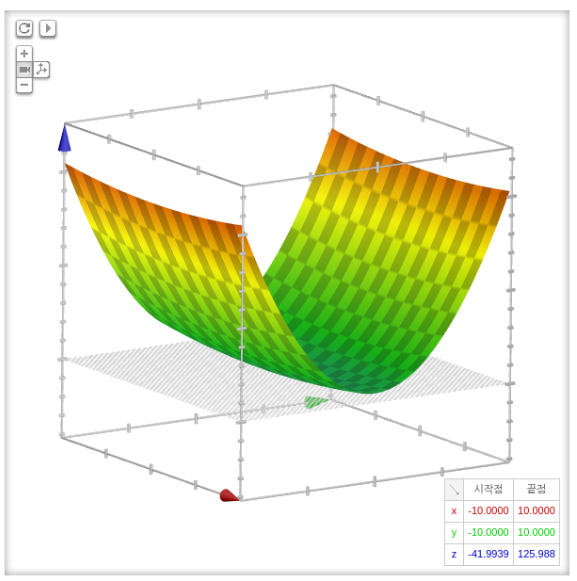
그래프를 보면, x축으로는 변화가 별로 없지만, y축은 U자를 그리며 격한 기울기의 변화를 보여준다.
위의 그래프와 같은 비등방성 함수(Anisotropy)에서 SGD를 수행하면, y축에 대해서는 지그재그로 움직여 최적해를 찾는데 시간이 더 소요되는 문제가 발생한다.

위와 같은 문제를 해결하기 위해, Momentum 과 AdaGrad 가 개발되었다.

2. Local minima 문제

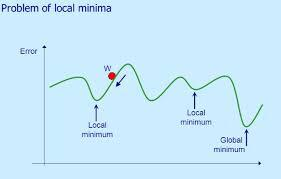
기울기가 0이 되는 지점이 손실함수의 최솟값이 아니라 극소값(Local minima)이라면 문제가 발생한다. 손실함수를 최소하지 못했는데, 더이상 매개변수가 갱신되지 않아 학습을 멈추는 것이다.

이 문제는 Momentum 에서 해결이 가능하다.