Abstract
현재 Contrastive Learning Framework는 Single Supervisory Signal을 활용한 Representation Learning에 중점
-
Representation Learning이란?
-
사용 가능한 모든 Supervised Signal을 활용하는 것이 중요
-
input 값들을 올바르게 classification 할 수 있도록 ‘new representation’을 뽑아 학습
-
모든 모델은 마지막에 선형으로 분류 → 데이터의 차원(특징)을 변형
-
Single Supervisory Signal의 사용은 unseen data와 downstream tasks에 대한 효과를 제한
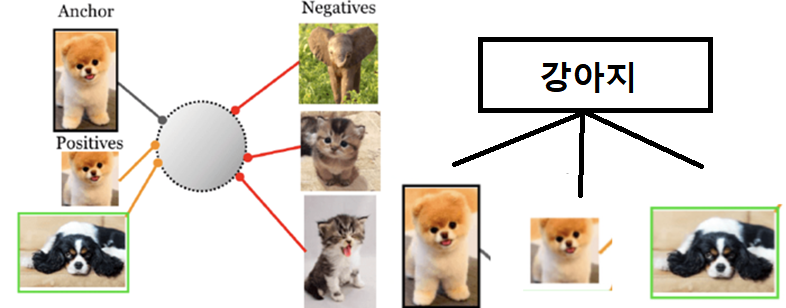
A Hierarchical Multi-Label Representation Learning Framework는 가능한 모든 label을 사용할 수 있고 class 사이의 Hierarchical Relationship을 보존
Hierarchy Preserving Losses
- apply a Hierarchy Penalty to the Constastive Loss
- enforce the Hierarchy Constraint
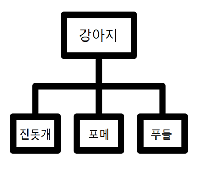
Introduction
실제 세계에서 Hierarchy Multi-Label은 매우 자연스러운 현상
Hierarchical Relationship은 class 간의 관계를 효율적으로 나타내는 역할

그러나, 이러한 관계는 learning task에서 거의 활용되지 않으며 기존의 supervised approach는 class를 flat list로 구성하는 것을 선호
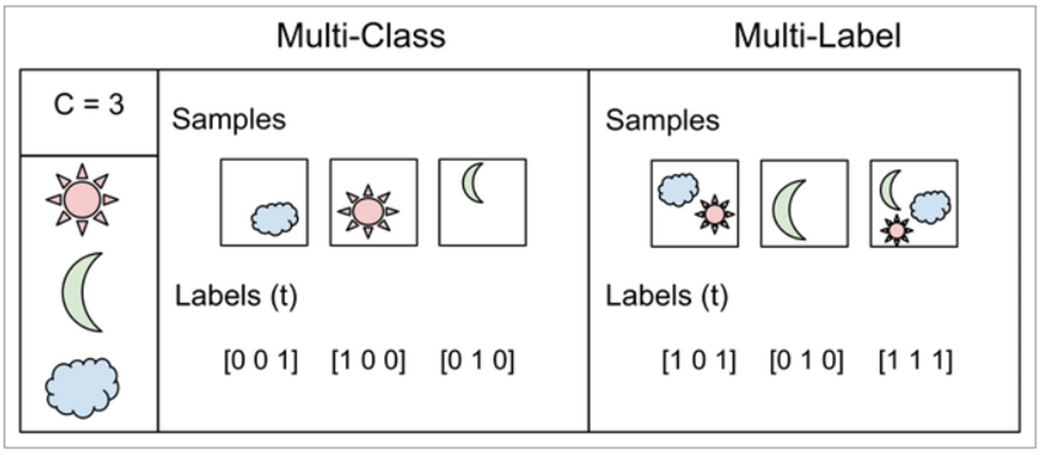
Unknown downstream task와 unseen data로 일반화 하기 위해 embedding function은 data를 간결하고 정확하게 표현해야 하며 hierarchical categorization 보존 필요
Multi-Label Learning을 통해 label 간의 관계 정보 활용
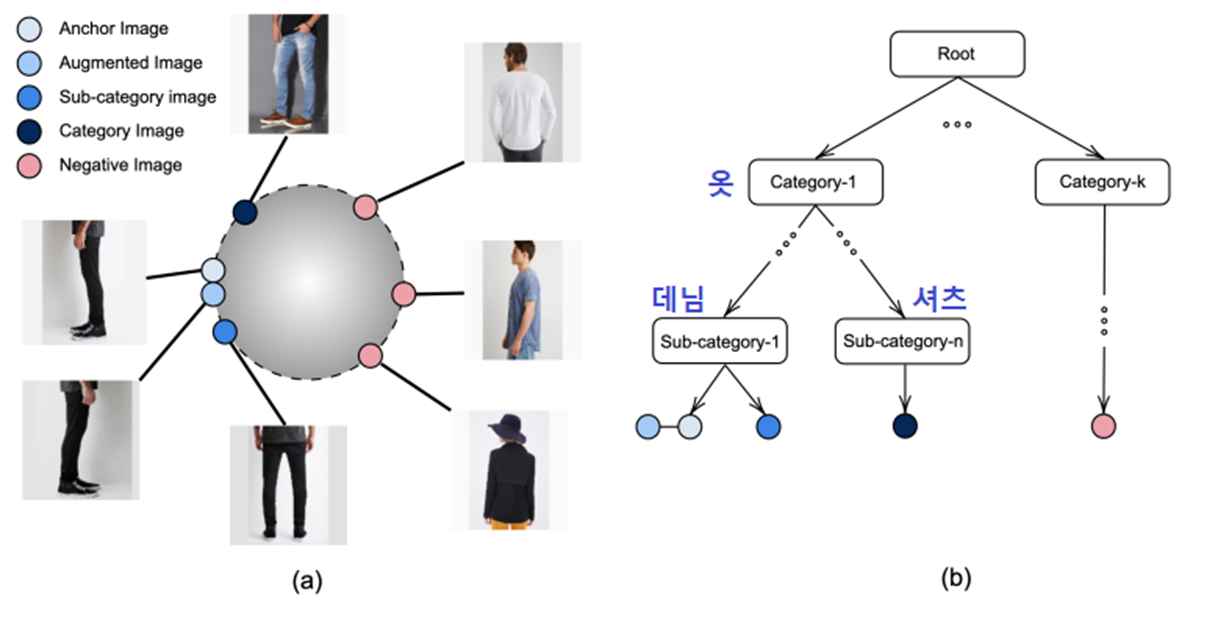
Hierarchical Multi-Label Setting에서 각 data point는 multiple dependent label을 가지고 label 간의 관계는 hierarchy 가장 표현
Hierarchy Structure을 활용하면 높은 분류 정확도를 가짐
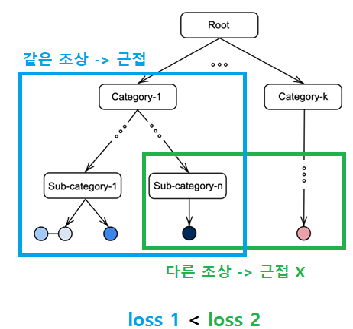
본 논문은 두 가지 새로운 loss를 제안 ( + 두 가지 loss 조합)
- Hierarchical Multi-Label 간의 관계를 활용
- Representation Space에서 label 관계를 유지할 수 있는 Representation 학습
Hierarchical Multi-Label Contrastive Loss는 label space에서 anchor 이미지와 일치하는 이미지 사이의 근접성에 따라 Penalty 적용
Hierarchical Contrastive Enforcing Loss는 Hierarchy Violation 방지
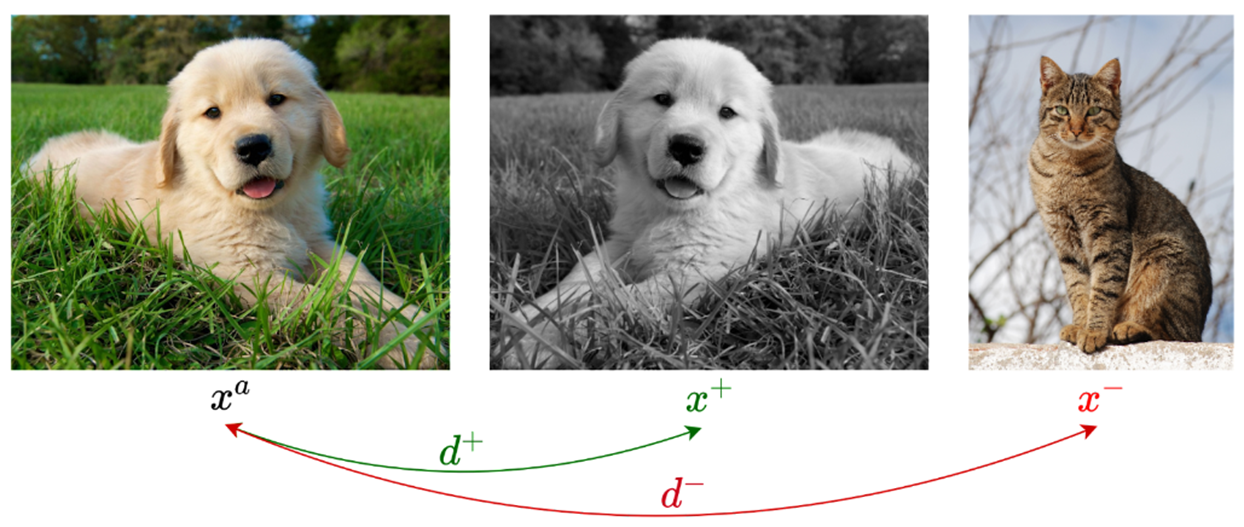
Contrastive Learning
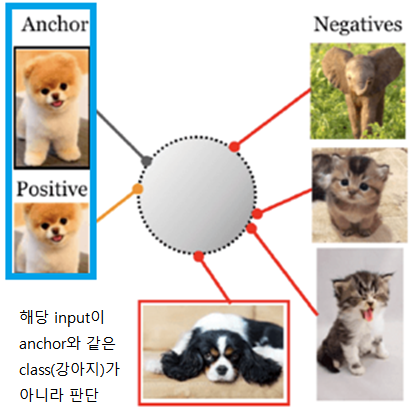
여러 이미지들 중 비슷한 이미지 pair (positive)를 서로 가깝게 하고 비슷하지 않은 이미지 pair (negative)는 멀리 떨어지게 함
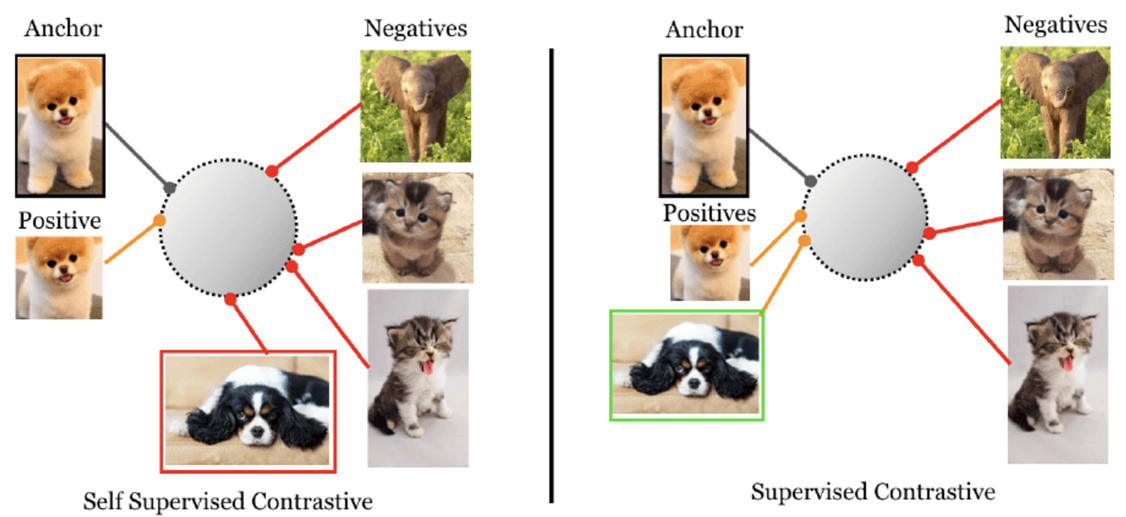
자기 자신에 의해 파생된 labeling data로 학습 → Self-Supervised Learning
Self-Supervised Contrastive Learning Loss
- i는 anchor image
- i는 A에 속해있고 A = {1,…, 2ㅜ} = 학습 데이터 N개 + 증강 데이터 N개 (multi-view data)
- k는 anchor를 제외한 모든 이미지, 2N-1개
- 분자는 anchor와 positive sample
- 분모는 anchor와 2N-2개의 negative + 1개의 positive
문제
: Self-Supervised Contrastive Learning은 같은 class도 negative sample로 인식
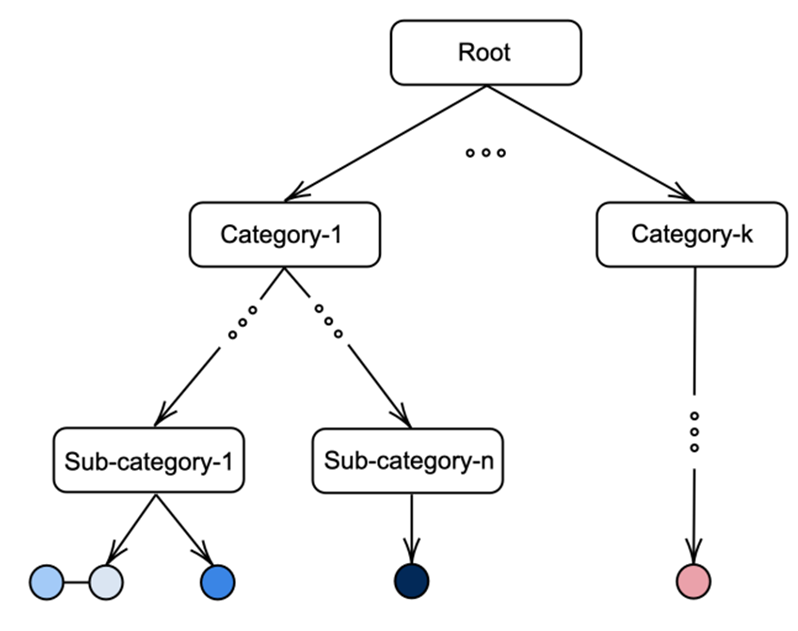
→ Supervised Contrastive Learning으로 해결
Supervised Contrastive Loss
- P는 i를 제외한 multi-view batch의 모든 positive samples (anchor의 증강 데이터)
- |P(i)|는 positive sample 개수
→ ‘나와 같은 class이냐’를 기준으로 Contrastive Loss를 줌
- 추가된 식, 여러 개의 positive
- Self-Supervisesd Contrastive Learning은 1개의 positive
문제
: Single Label에만 적용 가능
Hierarchical Multi-label Contrastive Learning
Level l에서 와 positive 이미지 쌍에 대한 loss
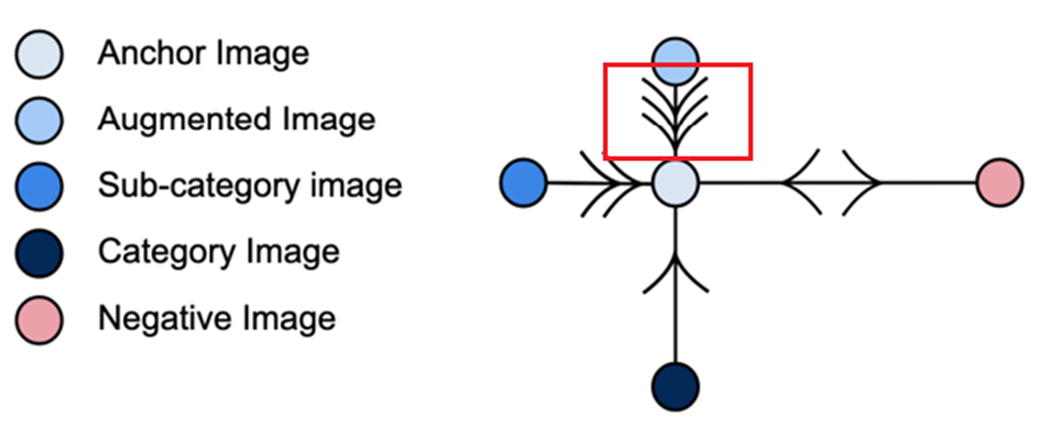
- L as the set of all label lavels, and l is a level in multi-label
- p is the set of positive images for anchor image indexed by i
Hierarchical Multu-label Contrastive Loss
높은 level에서 구성된 이미지 쌍에 더 높은 Penalty를 적용하여 가깝게 함
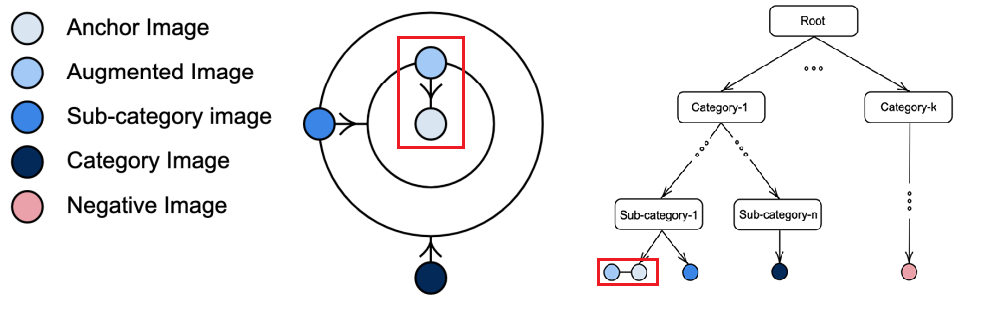
Hierarchical Constraint Enforcing Loss
-
Hierarchical Constraint Enforcing Loss는 Representation Learning Setting에서 Hierarchical Constraint를 시행
Hierarchical Constraint는 data point가 class에 속할 경우 상위 class에도 속해야 함을 보장
더 높은 Hierarchy의 confidence score > 더 낮은 Hierarchy의 confidence score

- Level l-1 에서의 pair loss > level l 에서 maximum loss
Hierarchical Multi-Level Constraint Enforcing Contrastive Loss
- 위 두 loss를 결합하여 Hierarchical Multi-Level Constraint Enforcing Contrastive Loss 형성
- HiconE 에 lambda term을 추가 → Hierarchical Constraint Enforcing term과 level penalty를 갖는 loss 제공
Hierarchical Batch Sampling Strategy
-
Sampling의 중요성 강조 : 유익하고 안정적인 example을 선택하는 것이 중요
많은 양의 Hard positive/negatives → 성능향상
Hierarchical Multi-level Setting에서는 모든 Hierarchy level에서 각 batch마다 anchor image에 대한 충분한 representation 필요
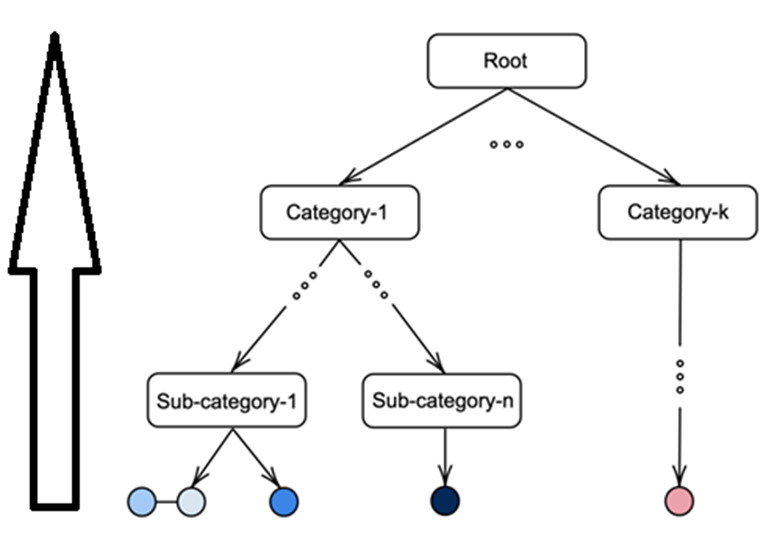
Experiments
세 가지 downstream task에서 loss 평가
- Image Classification
- Image Retrieval Accuracy on sub-category
- NMI for Clustering Quality
Datasets
seen/unseen으로 분리하여 seen sets으로 encoder network 학습
unseen sets에 대한 접근 방식과 관련 baseline의 성능 평가
-
DeepFashion Dataset
-
800K 이상
-
3 level
-
Category
-
ProductID
-
Variation(color, sub style…)

-
- ModelNet40
- 40 classes
- 3183개의 CAD 모델로 구성
- 2 level
- Category
- CAD Image ID
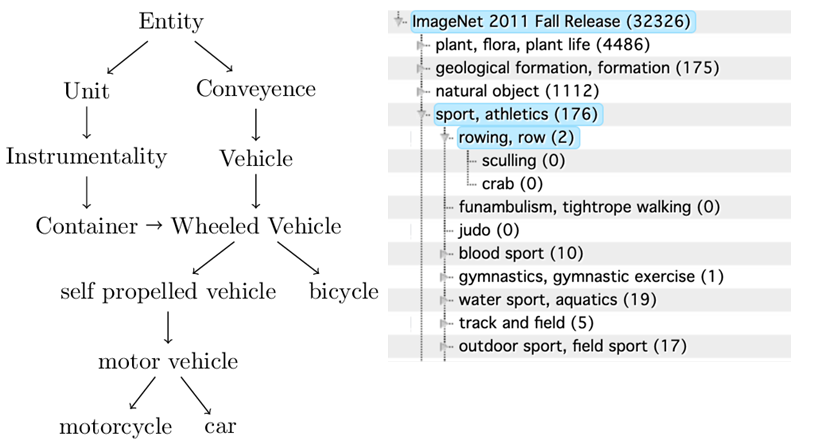
- ImageNet
-
WordNet 계층 구조
-
14,197,122 장
-
- iNaturalist
-
5,089 catefories
-
579,184 training images
-
95,986 validation image

-
Experiments Implementation Details
Pairing이 낮은 level에서 positive pair, 높은 level에서 negative pair 일 수 있으므로 Loss 계산은 가장 높은 level부터 계산
Classification Accuracy
- Unsupervised Contrastive Loss : SimCLR
- Two Supervised Learning Losses Function : Cross Entropy and Supervised Contrastive Loss(SupCon)
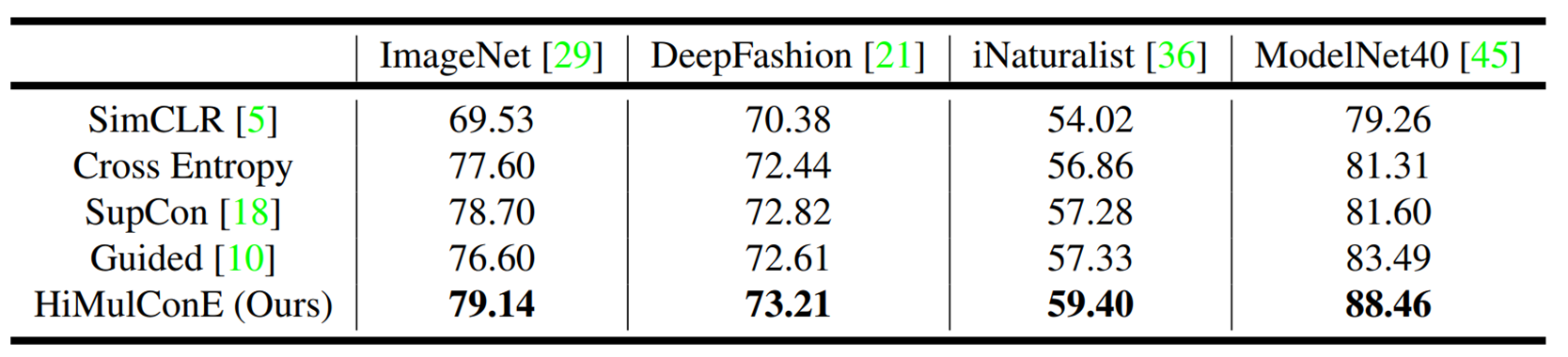
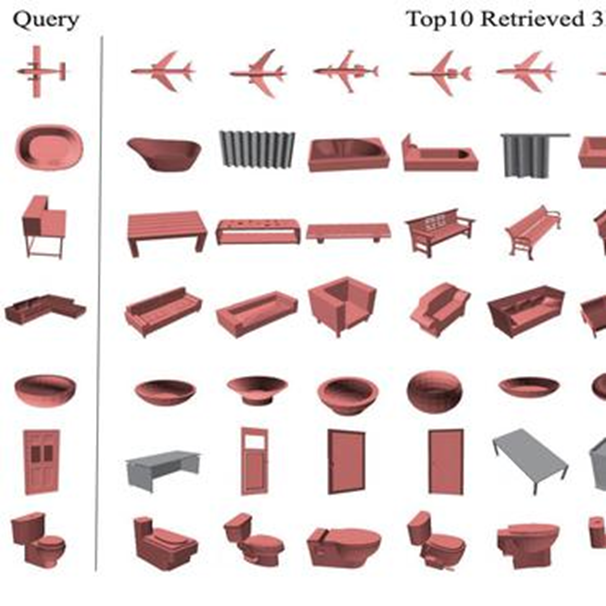
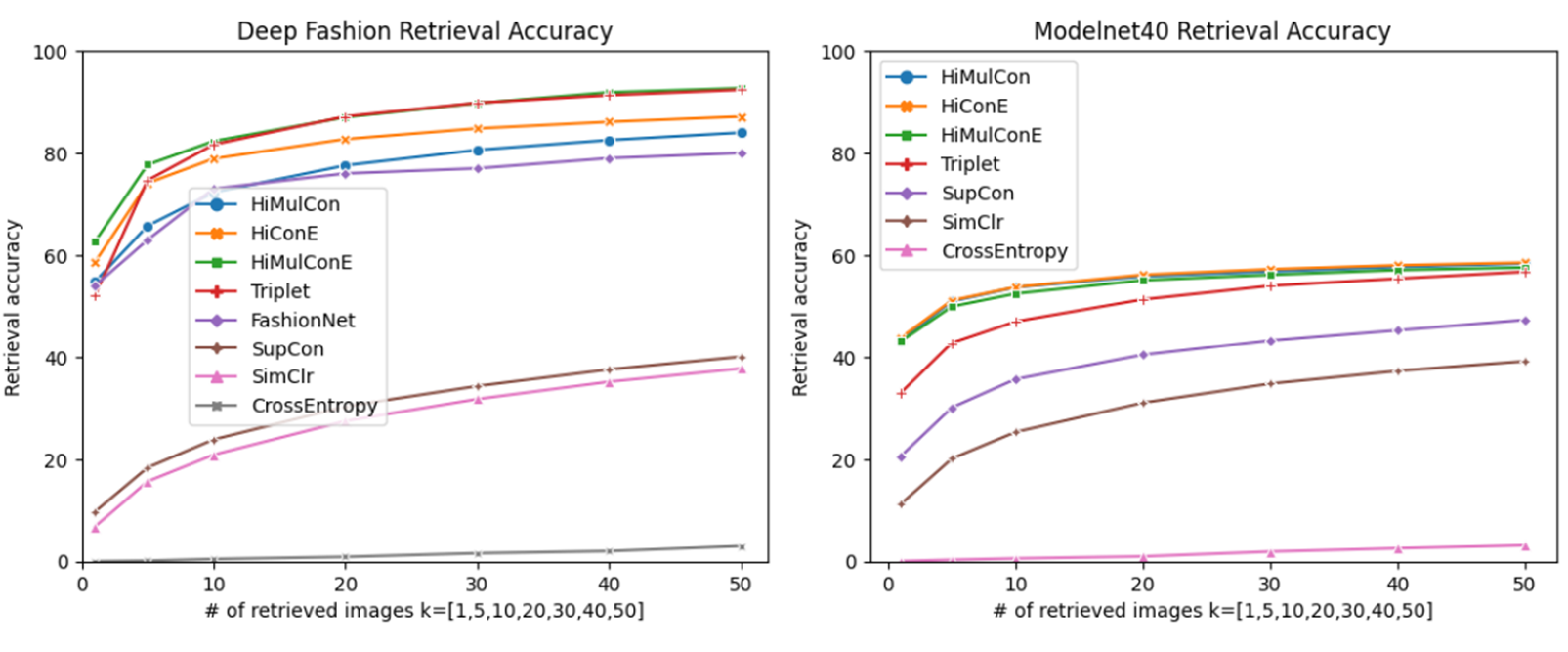
Image Retrieval Accuracy
해당 task는 쿼리 이미지와 동일한 class의 이미지를 검색
topK Accuracy는 쿼리 이미지 class가 검색된 topK 결과에서 동일한 class의 이미지를 찾을 수 있는지 여부를 측정하는 데에 사용
Full datasets
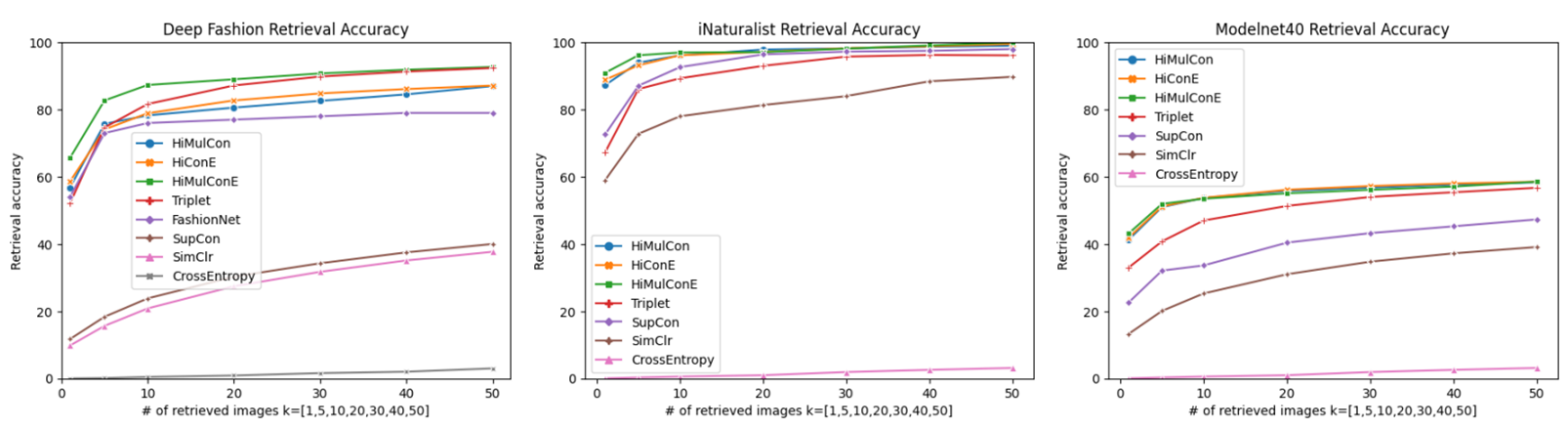
HiMulConE가 더 작은 k에서 더 큰 accuracy를 보임
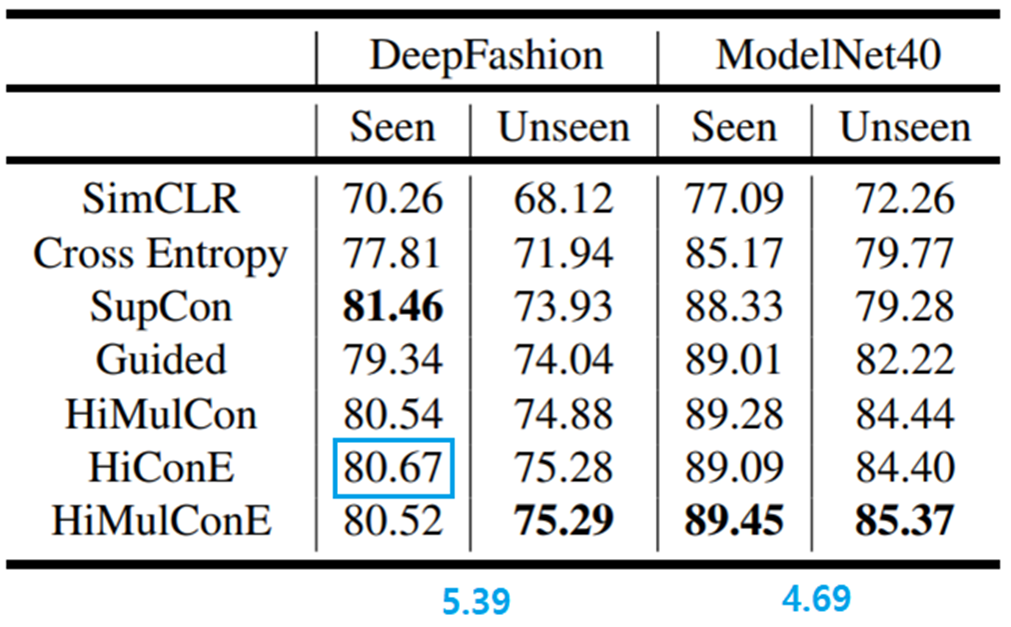
Unseen splits
Generalizability to Unseen Data - Classification
-
HiConE는 주변 level의 의미관계 exploit, 임베딩 공간에서 쌍 사이의 거리와 상관되는 크기로 Penalty 부여
HiMulCon은 level 차이에 기반한 고정된 Penalty로 label 공간에서 그들 사이의 거리에 대한 쌍을 Penalty로 만듦
HiMulConE는 level과 embedding space, 모든 차이 활용 가능
-
HiConE가 트리의 서로 다른 level에서 의미 중복이 있는 dataset(DeepFasion)에서 더 높은 성능
의미적으로 잘 분리된 dataset(M40)에서 격차가 작음
Generalizability to Unseen Data - Image Retrival
-
unseen data만 사용
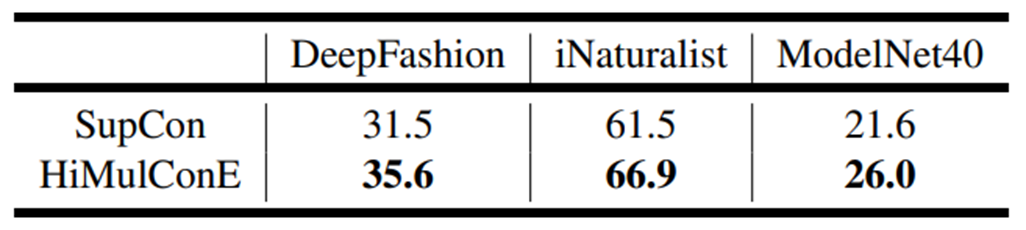
-
base line보다 더 나은 성능 → task의 Generalization
Embedding Space는 label-space hierarchy 보존
Generalizability to Unseen Data - Clustering
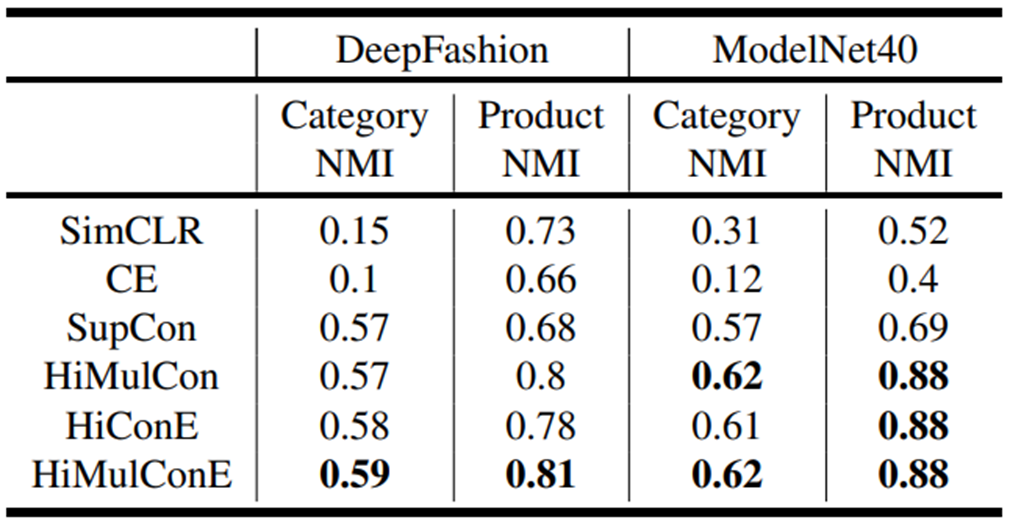
-
base line보다 나은 성능은 Category 내의 sub-category에 대한 separability
represenatation space에서 label 간의 Herarchical Realationship 보존
Conclusion
-
충분한 data가 없을 때 standard supervised나 self-supervised approach를 통해 사용 가능한 모든 label을 활용하기 위한 Framework 제안
-
Downstream task와 unseen data에 대한 Generalization
