[알고리즘] KMP 알고리즘

KMP 알고리즘이란?

KMP 알고리즘은 문자열에서 특정 문자열을 검색하는 (패턴 매칭) 알고리즘이다.

Brute Force 방식

가장 간단히 생각할 수 있는 방식은 Brute Force 알고리즘이다.
아래 상황에서 문자열 검색을 위해 필요한 시간 복잡도는 O(NxM)이 된다. (2중 for문 사용)

• 본문 문자열의 길이 : N
• 찾으려는 문자열 길이 : M

KMP 알고리즘

역시 Brute Force 방식은 대부분의 경우의 최선이 아니다. (매우 느림)
KMP 알고리즘을 한문장으로 정의하면 불일치가 발생하기 직전까지 같았던 부분을 활용하여 검색을 진행하자 라고 정의할 수 있다.
우선 KMP 알고리즘을 이해하기위해 4단계로 나눠 설명한다.

1. 접두부, 접미부, 경계

보통 KMP 알고리즘을 설명할때 3가지 용어를 많이 사용한다.
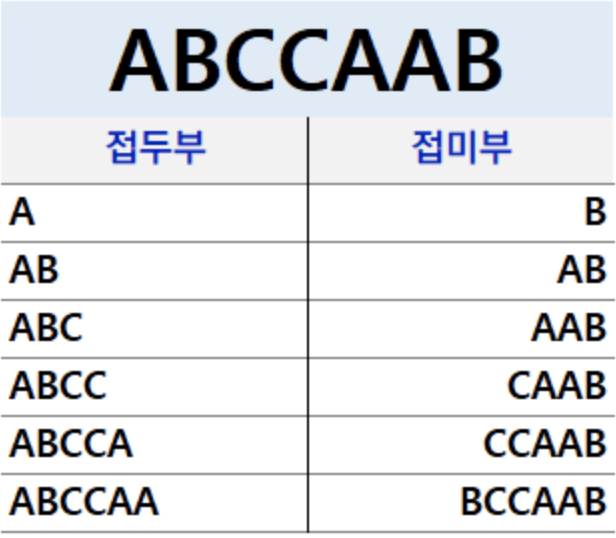
아래 그림을 보면 접두부, 접미부를 쉽게 이해할 수 있으며
경계란, 아래의 접두부와 접미부가 같을 때 그 접두부 혹은 접미부를 경계라고 한다.
KMP 알고리즘은 이러한 경계를 최적화하기 위한 지점으로 삼는다.

2. KMP 알고리즘의 개요

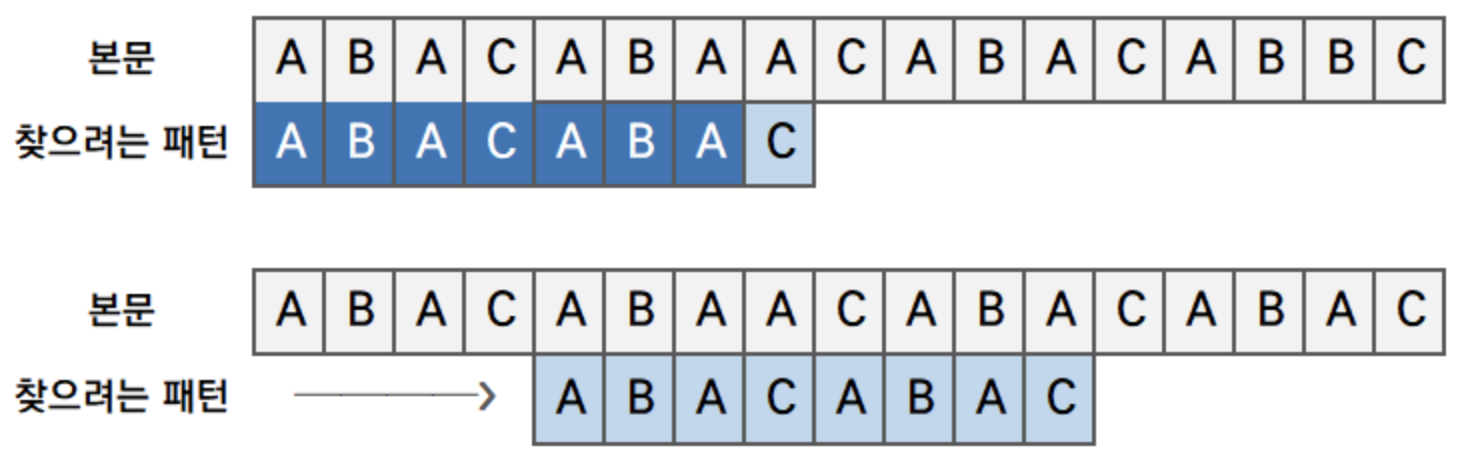
1. 본문이 되는 문자열에서 찾으려는 패턴을 특정 위치에 둔다.
2. 일부가 일치하지 않는다면, 불일치한 부분을 제외한 직접까지 일치하는 패턴에서 최대 길이의 경계를 찾는다.
3. 선택한 경계에서 접두부, 접미부를 파악하고 찾으려는 패턴을 접미부의 시작 문자열까지 이동시킨다. (경계가 없다면 처음 불일치했던 부분까지 패턴 이동)

하지만 매번 움직일 때마다 경계를 찾으려면 접두부, 접미부를 반복 분석해야하므로 이를 최적화 하기 위해
이동 경로 테이블을 만들어야 한다.

3. 이동경로 테이블 만들기

패턴 내에서 해당 인덱스까지의 패턴중 가장 큰 길이의 경계를 저장해둔다.
해당 위치에서 틀렸을 때 건너뛰어줄 크기를 뜻함

public static void getPi() {
	// j = 접두사 인덱스, i = 접미사 인덱스
    int j = 0;
    // 패턴을 처음부터 돌면서 체크 
    for (int i = 1; i < pattern.length(); i++) {
    	// 처음 접두사가 아니면서 일치하지 않으면, 반복되는 패턴의 앞부분으로 변경 
        // 만약 반복되는 패턴이 없으면, j = 0 까지 돌아감 
        while(j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
        	j = pi[j-1];
        }
        
        // 일치할때, 접두사의 길이 저장 
        // 현재 맞은 idx의 +1은 길이이자, 다음 체크할 idx가 됨
        if (pattern.charAt(i) == pattern.charAt(j)) {
        	pi[i] = ++j;
        }
    }
}

4. 전체 문자열에서 KMP 실행

일치했던 패턴에서의 경계를 이용해서 건너뛰는 방식으로 체크한다.

public static void kmp() {
	// 패턴 내 일치체크 idx
    int j = 0;
    // 전체 문자열 순회 
    for (int i = 0; i < all.length(); i++) {
    	// 맞는 위치가 나올 때까지 j-1칸의 공통 부분 위치로 이동 
        while(j > 0 && all.charAt(i) != pattern.charAt(j)) {
        	j = pi[j - 1];
        }
        // 맞는 경우 패턴의 끝까지 확인했으면 정답
        if (all.charAt(i) == pattern.charAt(j)) {
        	if (j == pattern.length() - 1) {
            	answer = 1;
                break;
            } else {
            	j++;
            }
        }	
    }
}