알고리즘
1.순열 (Permutation) 구현

순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다.예를들어 1,2,3 수열이 있을경우 이에 대한 순열은 다음과 같이 6가지가 있다.순열을 구현하는데는 다음과 같은 2가지 방식만 알아놓으면 좋을 것 같다. DFS + 방문처리를 이용한 방식으로 순열을 구하는 과정에
2.[알고리즘] 분할 정복(divide & conquer)
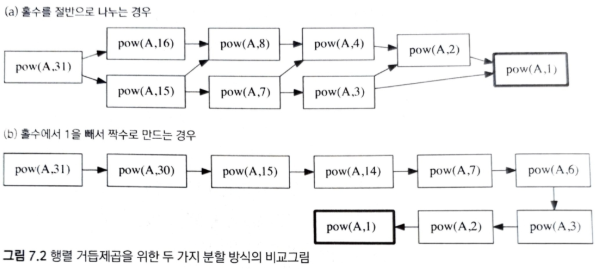
분할 정복이란 유명한 알고리즘 디자인 패러다임으로, 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산하고, 각 부분 문제의 답으로 전체 문제의 답을 계산해내는 방법이다. 분할 정복 알고리즘은 크게 아래 세가지 구성요소를 가진다
3.[알고리즘] 세그먼트 트리
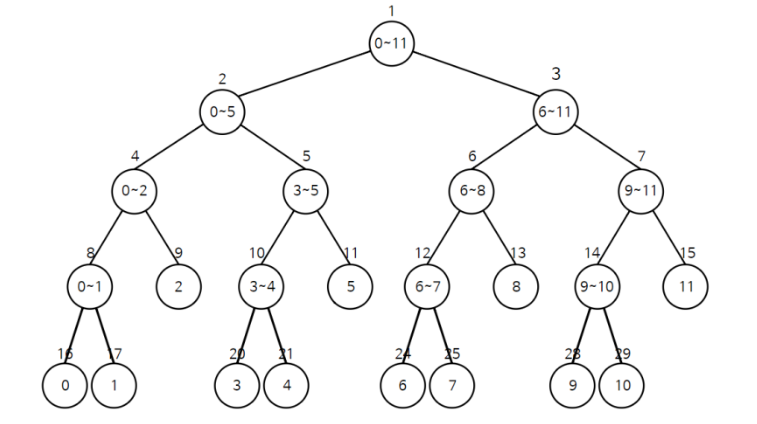
특정 구간합을 빠르게 구하기 위해 만들어진 자료구조이다.어떤 숫자 배열에 대해, 1.특정구간의 합 구하기 연산과 2.특정 위치의 값 바꾸기 연산이 있을 때 이를 배열로 구현하는 것과 세그먼트 트리로 구하는 방식의 시간 복잡도는 다음과 같다. 위의 특징처럼 세그먼트 트리
4.[알고리즘] 최대공약수, 최소공배수

유클리드 호제법은 최초의 알고리즘으로 불리며 최대공약수(Greatest Common Divider)를 구하기 위한 알고리즘이다. 유클리드 호제법은 다음과 같다. (증명은 위키참조..) a >= b일 때, GCD(a, b) = GCD(b, r) (r : a % b) 즉
5.[알고리즘] 외판원 순회 문제

외판원 순회 문제
6.[알고리즘] 투 포인터 알고리즘

리스트에 순차적으로 접근해야 할 때 2개의 점의 위치를 기록하면서 처리하는 알고리즘만약 투 포인터 알고리즘을 사용하지 않으면, 이중 반복문 때문에 시간 복잡도가 O(n^2)이 된다. 그러나 투 포인터 알고리즘을 사용하면 O(N)으로 줄일 수 있음투 포인터 알고리즘은 크
7.[알고리즘] 이분탐색, lower / upper bound
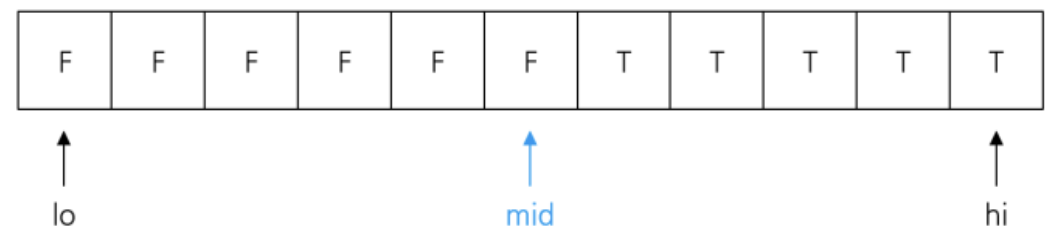
이분탐색이 정확히 원하는 값을 찾는 것이라면, lower/upper bound는 원하는 값의 경계 인덱스를 찾는 방법으로 중복된 요소나 타겟의 상한 하한을 찾는 경우 등 다양한 방식으로 활용될 수 있다. 이분탐색, lower bound, upper bound를 코드 예
8.[알고리즘] 가장 긴 공통 부분 문자열 (LCS - Longest Common SubString)

LCS는 가장 긴 공통 부분 문자열을 뜻한다. 문자열은 끊어지지 않는 문자들의 연속을 뜻한다. 기본적으로 O(n^2) 풀이가 일반적이다. 기본적인 점화식은 아래와 같다. DPi : (i,j)를 끝으로 하는 가장 긴 부분 문자열의 길이DPi = DPi-1 + 1 (Ai
9.[알고리즘] 그래프 알고리즘 1. 다익스트라 알고리즘

하나의 정점에서 다른 모든 정점까지의 최단 거리를 구할 때 사용. 음수 가중치 있을 때는 사용불가능. (현실 세계에서 사용하기 적합)Greedy한 접근법을 보인다. (특정 상황에서 최적 판단)코스트(출발 노드와 거리) 테이블을 초기화 한다. (INF로 초기화)출발 노드
10.[알고리즘] 위상 정렬(Topology Sort)

순서가 정해져있는 작업을 차례로 수행해야할 때 그 순서를 결정해주기 위해 사용하는 알고리즘방향 그래프, 사이클이 없는 그래프에서만 적용이 가능하다 (DAG : Directed Acyclic Graph)모든 원소를 방문하기 전에 큐가 빈다면 사이클 존재 그래프에 사이클이
11.[알고리즘] Trie 자료구조
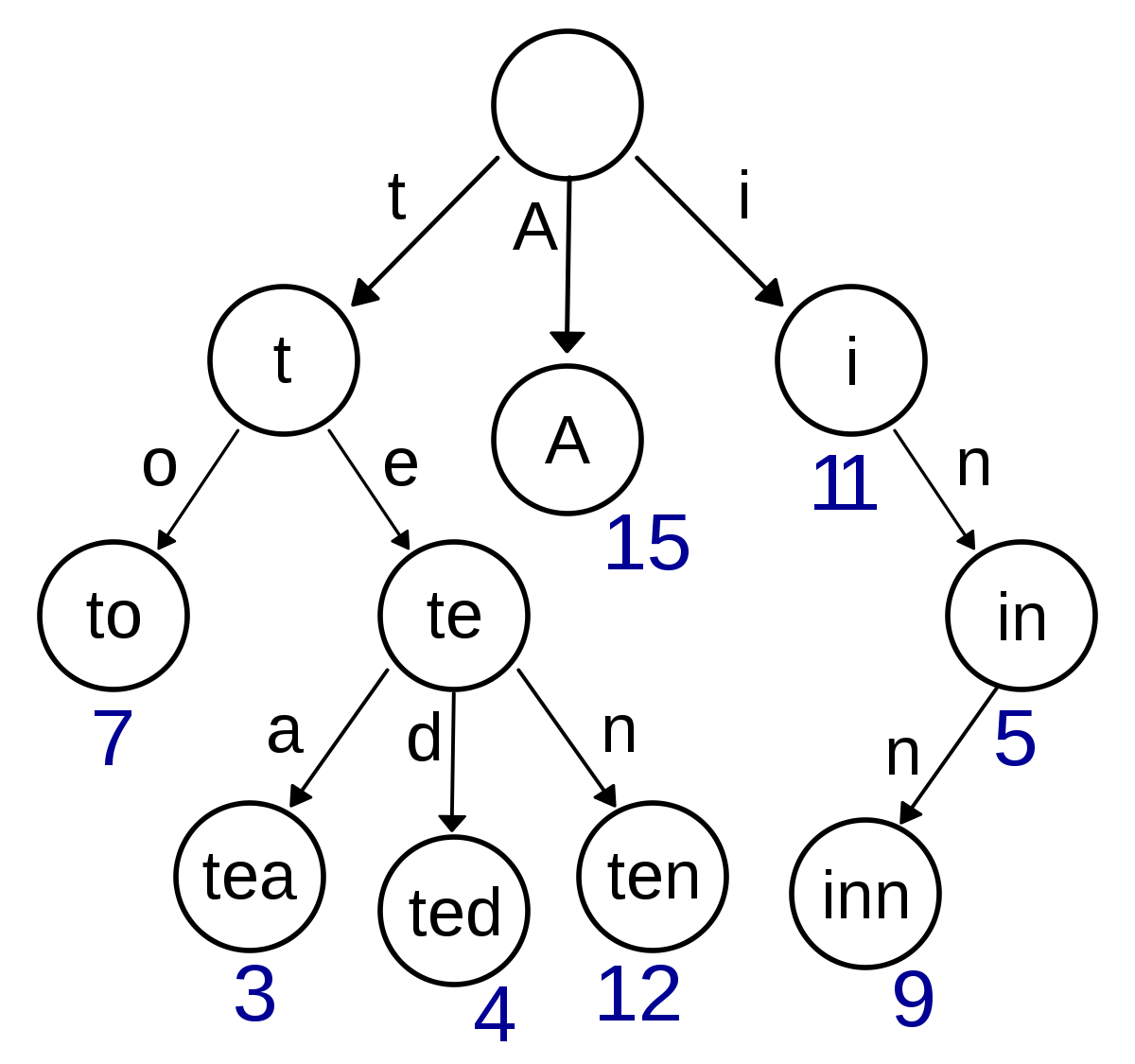
일반적인 이진트리에서 검색시에 O(logN)의 시간 복잡도를 가지게 된다. 하지만 이진트리 형태이더라도 문자열을 저장하고 있다면 문자열 최대 길이가 M일 때, O(M\*logN)의 시간 복잡도를 가지게 된다. 이러한 문제를 해결하기 위해 O(M)의 시간복잡도를 가지는
12.[알고리즘] UNION-FIND 자료구조

UNION-FIND 유니온 파인드 자료구조는 '합집합 찾기'로 번역할 수 있다. 해당 자료구조에는 2가지 메서드가 있는데 기능은 아래와 같다. > 1. Void UNION(int a, int b) > - 원소 a, b를 하나의 집합으로 합침 > 2. int FIND(i
13.[알고리즘] 최소 신장 트리 (Kruskal, Prim 알고리즘)

그래프 내의 모든 정점을 포함하며 최소 간선을 가지는 트리n개의 정점을 가지는 그래프에서 최소 간선 수는 n-1개가 된다사이클이 존재하지 않는다.하나의 그래프에서 여러 신장 트리가 존재할 수 있다신장 트리 중에서 가중치의 합이 가장 적은 신장 트리를 뜻한다. 네트워크에
14.[알고리즘] KMP 알고리즘
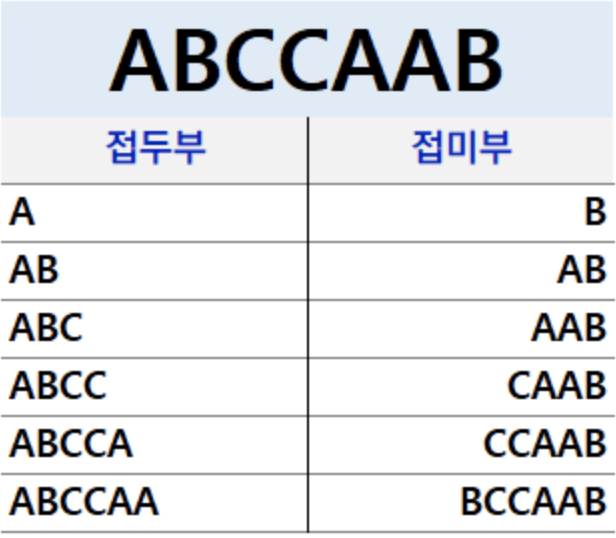
KMP 알고리즘은 문자열에서 특정 문자열을 검색하는 (패턴 매칭) 알고리즘이다.가장 간단히 생각할 수 있는 방식은 Brute Force 알고리즘이다.아래 상황에서 문자열 검색을 위해 필요한 시간 복잡도는 O(NxM)이 된다. (2중 for문 사용) 본문 문자열의 길이
15.[알고리즘] LCA 알고리즘
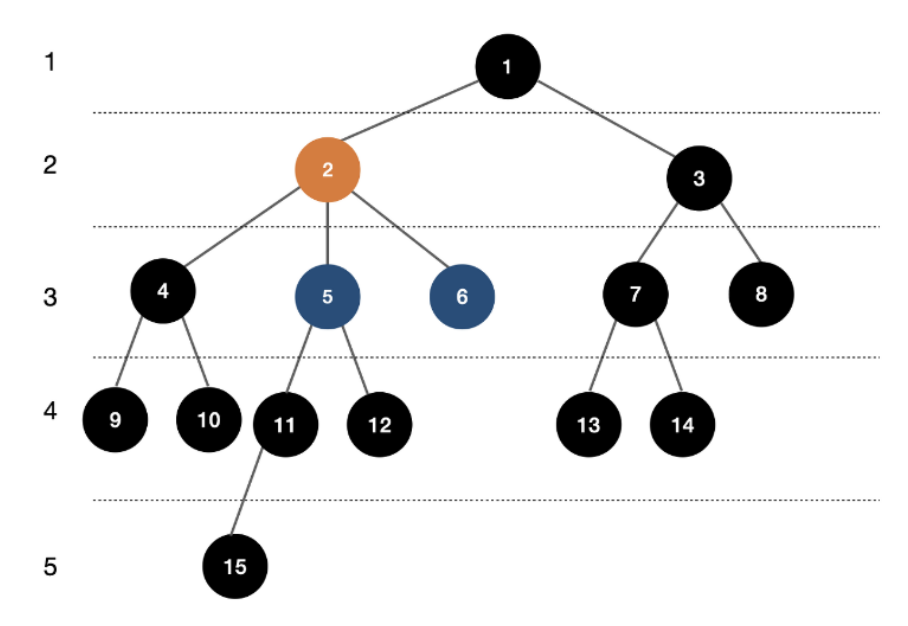
LCA 알고리즘은 트리에서 주어진 두개의 노드의 최소 공통 조상을 찾는 알고리즘이다. 예를 들어 아래 그림에서 5,6번 노드의 LCA는 2번 노드이다. 간단히 생각해볼 수 있는 LCA 알고리즘은 다음과 같다. 루트 노드를 기준으로 DFS를 통해 각 노드의 트리 높이와
16.[알고리즘] 타잔(tarjan) 알고리즘
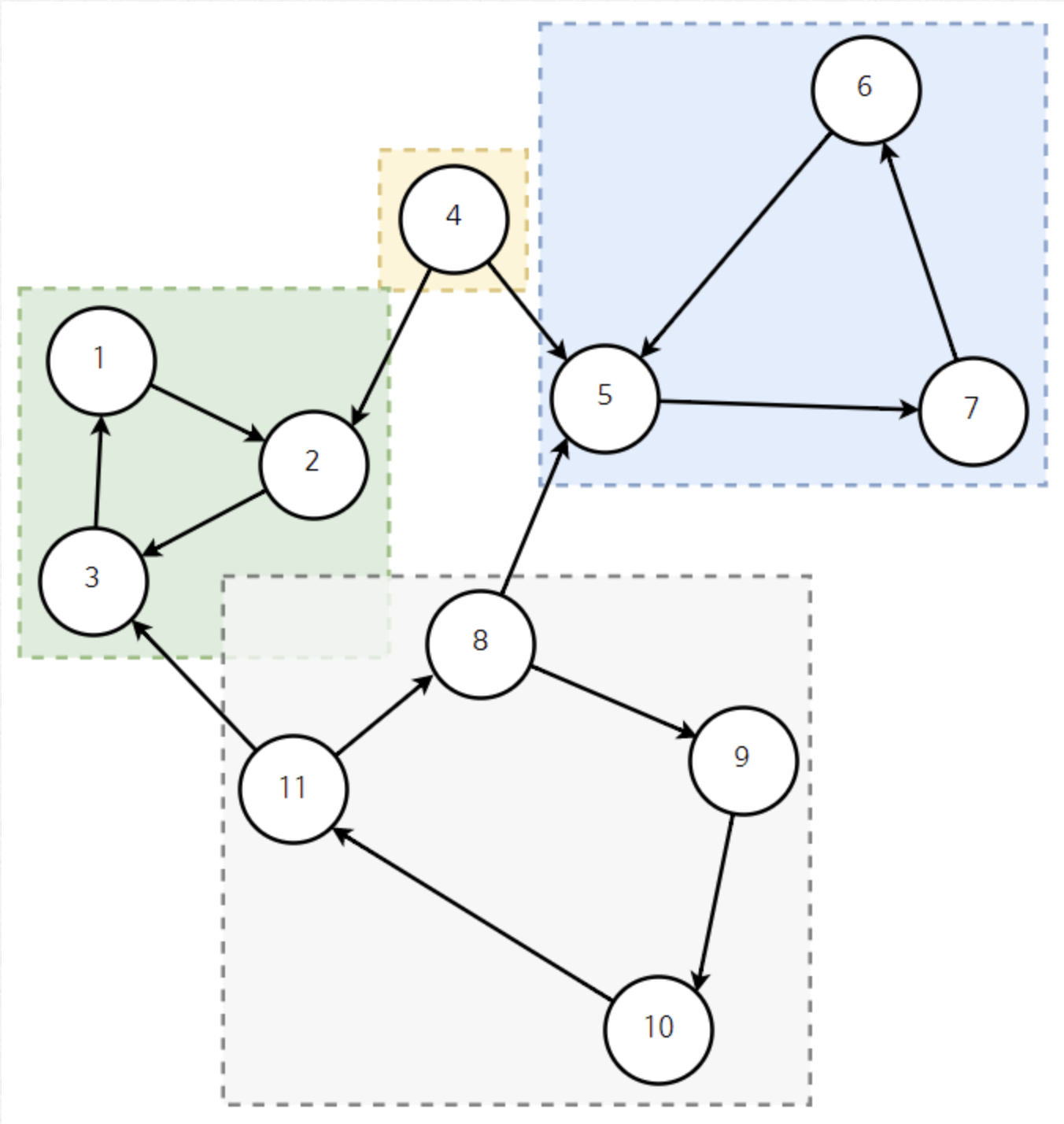
SCC (강한 결합 요소)란 그래프 내에서 강하게 결합된 정점들의 집합 이다.강하게 결합되었다는 뜻은 같은 SCC 내의 두 정점은 서로 도달이 가능하다는 뜻이다.SCC를 추출하는 알고리즘은 크게 코사라주 알고리즘, 타잔 알고리즘이 존재한다.그 중에 타잔 알고리즘은 구현
17.[알고리즘] 그래프 알고리즘 1. 벨만-포드 알고리즘

하나의 정점에서 다른 모든 정점까지의 최단 거리를 구할 때 사용. 다익스트라 알고리즘과 다르게 음의 가중치를 갖는 간선이 있어도 사용 가능하다.다익스트라 알고리즘은 매번 방문하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택해 나가는 반면(Greedy한 방식) 벨만-
18.[알고리즘] 가장 긴 증가하는 부분 수열 (LIS)

가장 긴 증가하는 부분 수열을 찾는 문제는 유명한 다이나믹 프로그래밍 문제이다.직관적인 O(N^2) 알고리즘과 좀 더 복잡한 O(NLogN) 알고리즘으로 나뉜다. O(N^2) 알고리즘은 다음과 같은 점화식을 통해 구할 수 있다.DPi : i번째 원소를 마지막으로 하는
19.[알고리즘] knapsack 알고리즘

knapsack 알고리즘은 제한된자원으로 최대의 이득을 얻는 유명한 다이나믹 프로그래밍 문제이다.knapsack 알고리즘은 크게 3가지 방식으로 나뉜다.Fractional knapsack : 물건을 분할해서 가방에 담을 수 있음 \-> 단순히 무게당 가치가 높은 것을