[알고리즘] 이분탐색, lower / upper bound

이분 탐색이란?

결정 문제에서 답이 i가 증가함에 따라 F, F, F .... F, T, T .., T 와 같이 경계를 가지고 분포하는 경우 처음으로 결정 문제가 T가 되는 i값을 찾는 것이다.

구현 방법

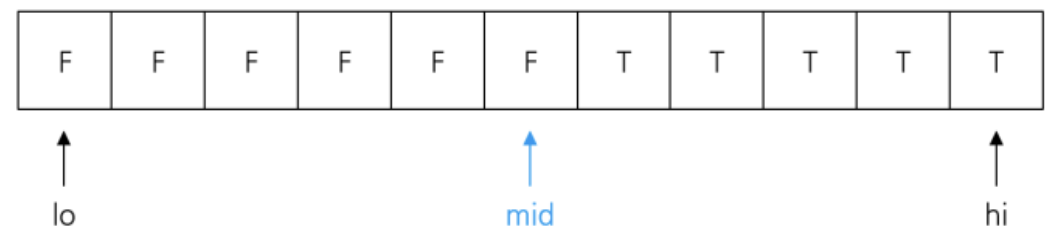
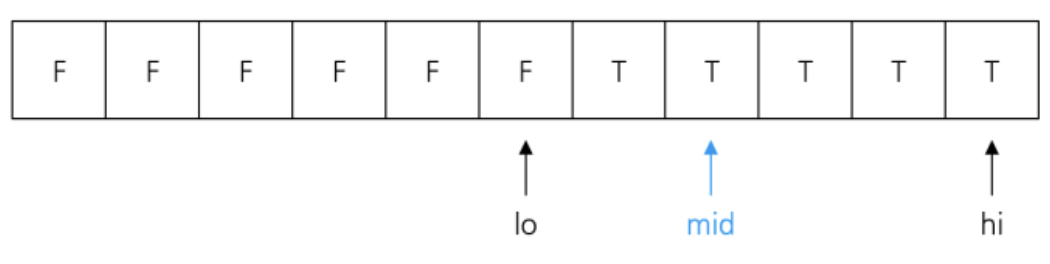
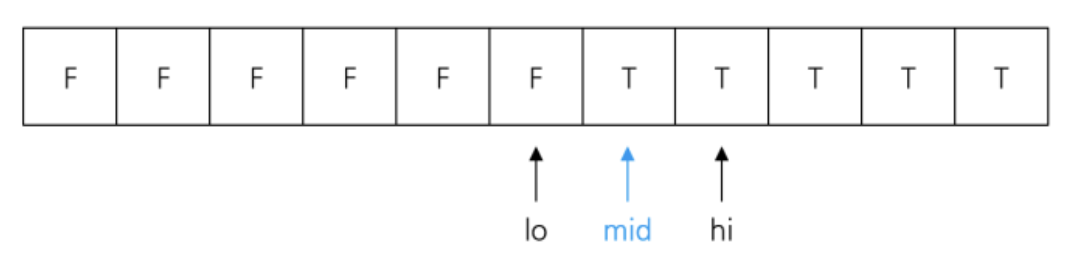
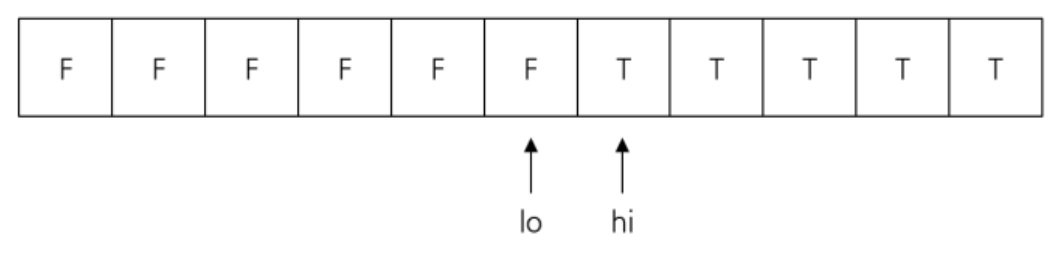
이분 탐색의 구현은 Check(lo) != Check(hi)가 되도록 초기 lo, hi 값을 설정해준 뒤 lo + 1 < hi인 동안 mid = (lo + hi) / 2를 구해서 Check(lo) == Check(mid)라면 lo = mid를, Check(hi) == Check(mid)라면 hi = mid를 해주면 된다.
이분 탐색이 끝나면 lo, hi는 결정 문제의 답이 바뀌는 경계에 위치하게 되며, 만약 결정 문제의 답의 분포가 F~T인테 정답이 가장 큰 F라면 lo를, 가장 작은 F라면 hi를 출력해주면 된다.

구현

public static int binarySearch() {
	int lo = 0, hi = maxVal;
    //CheckList
    //1. Check(lo) = T, Check(hi) = F를 만족하는가?
    //2. lo는 정답이 될 수 있는 모든 범위를 나타낼 수 있는가?
    
   	while(lo + 1 < hi)
    	int mid = (lo + hi) / 2;
        if (Check(mid)) lo = mid;
        else hi = mid;
    }
    return lo; //뭘 리턴할지는 조건에 따라 다르게 
}

lower/upper bound

이분 탐색의 대표적인 예시로는 lower bound / upper bound가 있다.
lower bound는 정렬된 배열에서 특정값 이상인 원소가 처음 등장하는 위치를 찾고
upper bound는 정렬된 배열에서 특정값 초과인 원소가 처음 등장하는 위치를 찾는다.
lower bound는 k <= v[i]인 i의 최솟값을 반환한다. 만약 v의 모든 원소가 k보다 작으면 v의 마지막 다음칸의 위치를 반환한다.
upper bound는 k < v[i]인 i의 최솟값을 반환한다. 이 경우도 v의 모든 원소가 k보다 작거나 같다면 v의 마지막 다음칸의 위치를 반환한다.

구현 (Lower Bound)

public static int lowerBound(int[] arr, int x) {
	int n = arr.length;
    int lo = -1, hi = n;
    while(lo + 1 < hi) {
    	int mid = (lo + hi) / 2;
        if (arr[mid] < x) lo = mid;
        else hi = mid;
    }
    return hi;
}

• 종료되었을 때, arr[lo] < x, arr[hi] >= x 를 만족하므로 hi값을 return한다.

구현 (Upper Bound)

public static int upperBound(int[] arr, int x) {
	int n = arr.length;
    int lo = -1, hi = n;
    while(lo + 1 < hi) {
    	int mid = (lo + hi) / 2;
        if (arr[mid] <= x) lo = mid;
        else hi = mid;
    }
    return hi;
}

• 종료되었을 때, arr[lo] <= x, arr[hi] > x를 만족하므로 hi값을 return한다.