
Brute-force: 카펫 [Lv2]
문제 설명
Leo는 카펫을 사러 갔다가 아래 그림과 같이 중앙에는 노란색으로 칠해져 있고 테두리 1줄은 갈색으로 칠해져 있는 격자 모양 카펫을 봤습니다.

Leo는 집으로 돌아와서 아까 본 카펫의 노란색과 갈색으로 색칠된 격자의 개수는 기억했지만, 전체 카펫의 크기는 기억하지 못했습니다.
Leo가 본 카펫에서 갈색 격자의 수 brown, 노란색 격자의 수 yellow가 매개변수로 주어질 때 카펫의 가로, 세로 크기를 순서대로 배열에 담아 return 하도록 solution 함수를 작성해주세요.
제한사항
- 갈색 격자의 수 brown은 8 이상 5,000 이하인 자연수입니다.
- 노란색 격자의 수 yellow는 1 이상 2,000,000 이하인 자연수입니다.
- 카펫의 가로 길이는 세로 길이와 같거나, 세로 길이보다 깁니다.
입출력 예
| brown | yellow | return |
|---|---|---|
| 10 | 2 | [4, 3] |
| 8 | 1 | [3, 3] |
| 24 | 24 | [8, 6] |
Solution
내 풀이
def solution(brown, yellow):
answer = []
yellow_area = set()
for i in range(1, yellow // 2 + 2):
if yellow % i == 0:
a, b = i, yellow // i
tmp = tuple(sorted([a, b]))
yellow_area.add(tmp)
yellow_area = list(yellow_area)
for aliquots in yellow_area:
len_col = aliquots[0] + 2
len_row = aliquots[1] + 2
if len_col * len_row - yellow == brown:
answer = [len_row, len_col]
break
return answer
yellow를 1부터 yellow // 2 + 1까지의 수로 나눠보면서 나머지가 0이 되면 나눈 수와 값을 오름차순 순서로 튜플로 만들어 yellow_area에 추가한다. 즉, yellow의 약수들을 저장하는 것이다.
그 다음 for문에서 yellow_area에 저장된 값들을 가져와서 이 값들로 카펫 가운데의 영역을 지정한다면, 그 때 생기는 borwn의 영역이 주어진 값과 동일한지 비교한다.
결과
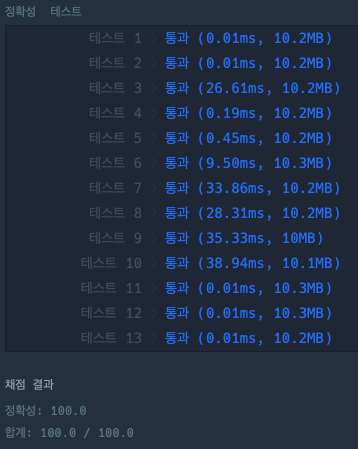
Best Code
def solution(brown, yellow):
for i in range(1, int(yellow**(1/2))+1):
if yellow % i == 0:
if 2*(i + yellow//i) == brown-4:
return [yellow//i+2, i+2]
원리 자체는 내가 만든 코드와 비슷하다. 하지만 내 코드에 비해서 더 효율적이고 길이가 압축적이다.
내가 for문에서 범위를 yellow // 2 + 2까지 했던 것을 이 코드에서는 yellow * (1/2) + 1까지이다.
그리고 내가 (yellow 영역의 가로길이 + 2) (yellow 영역의 세로길이 + 2) - yellow == brown 이라고 만든 것을 이 코드는
2*(i + yellow // i ) == brown - 4로 검증했다.
결과
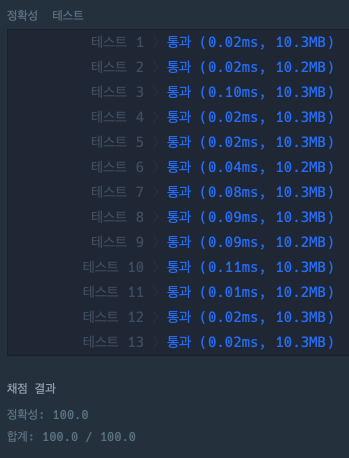
내 코드에 비해 결과 속도도 확실히 빠르다.
