다익스트라
- 다익스트라 알고리즘은 그래프에서
최단 거리를 구하는 알고리즘이다. 엣지는 항상 양수여야 한다는 제약 조건이 있다.

특정 노드에서 다른 노드들의 최단 거리를 구하는 문제가 주어졌을 때 다익스트라 알고리즘을 사용하면 문제를 해결할 수 있다.
다익스트라 알고리즘의 핵심 이론
1. 인접 리스트로 그래프 구현하기
- 먼저 다음과 같이 주어진 그래프를 인접 리스트로 구현한다. → 데이터를 자료 구조에 저장
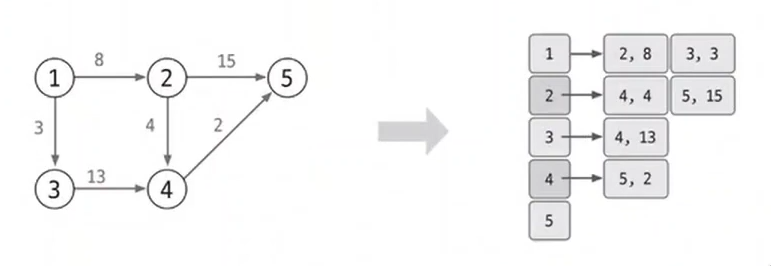
다익스트라 알고리즘은 인접 행렬에 구현해도 좋지만 시간 복잡도 측면, N의 크기가 클 것을 대비에 인접 리스트를 선택하여 구현하는 것이 좋다. 그래프의 연결을 표현하기 위해 인접 리스트에 연결한 배열의 자료형은 (노드, 가중치)와 같은 형태로 선언하여 연결한 점도 눈여겨보면 좋다.
2. 최단 거리 배열 초기화하기
- 최단 거리 배열을 만들고, 출발 노드는 0, 이외의 노드는 무한으로 초기화한다. 이때 무한은 적당히 큰 값을 사용하면 된다.
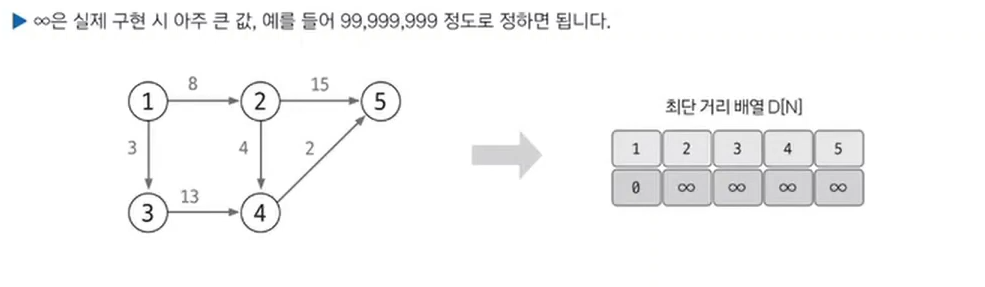
3. 값이 가장 작은 노드 고르기
- 최단 거리 배열에서 현재 값이 가장 작은 노드를 고른다. 여기서는 값이 0인 출발 노드에서 시작하면 된다.

4. 최단 거리 배열 업데이트하기
- 선택된 노드에 연결된 엣지의 값을 바탕으로 다른 노드의 값을 업데이트한다. 1단계에서 저장해 놓은 연결 리스트를 이용해 현재 선택된 노드의 엣지들을 탐색하고 업데이트하면 된다. 연결 노드의 최단 거리는 다음과 같이 두 값 중 더 작은 값으로 업데이트 한다.

5. 과정 3~4를 반복해 최단 거리 배열 완성하기
- 모든 노드가 처리될 때 까지 과정 3~4를 반복한다. 과정 4에서 선택 노드가 될 때마다 다시 선택되지 않도록 방문 배열을 만들어 처리하고, 모든 노드가 선택될 때까지 반복하면 최단 거리 배열이 완성된다.

출처 - 하루코딩

