벨만 포드

• 벨만-포드 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘이다.
• 음수 가중치 엣지가 있어도 수행할 수 있다는 특징이 있다.
• 전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있다.

벨만-포드의 핵심 이론

• 벨만-포드 알고리즘은 다음 3가지 단계의 원리로 동작한다.

1. 엣지 리스트로 그래프를 구현하고 최단 경로 리스트 초기화하기

• 벨만-포드 알고리즘은 엣지를 중심으로 동작하므로 그래프를 엣지 리스트로 구현한다.
• 또한, 최단 경로 리스트를 출발 노드는 0, 나머지 노드는 무한대로 초기화한다.

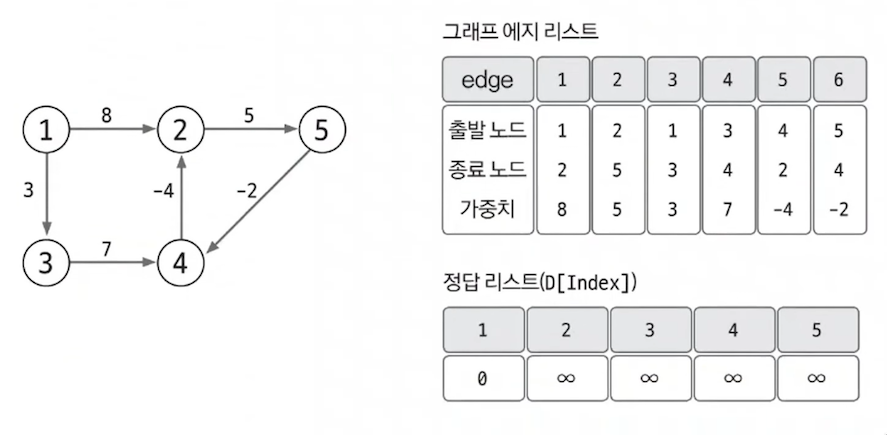
edge 클래스는 일반적으로 노드 변수 2개와 가중치 변수로 구성되어 있다.

2. 모든 엣지를 확인해 정답 리스트 업데이트하기

• 최단 거리 리스트에서 업데이트 반복 횟수는 노드 갯수 -1이다. 노드 갯수가 N이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 엣지의 최대 갯수는 N - 1이기 때문이다. 모든 엣지 E = (s, e, w)에서 다음 조건을 만족하면 업데이트를 실행한다.
• 업데이트 반복 횟수가 K번이라면 해당 시점에 정답 리스트의 값은 시작점에서 K개의 엣지를 사용했을 때 각 노드에 대한 최단 거리이다.

🌸 업데이트 조건과 방법

• D[s] ≠ ∞이며 D[e] > D[s] + w일 때 D[e] = D[s] + w로 리스트의 값을 업데이트 한다.

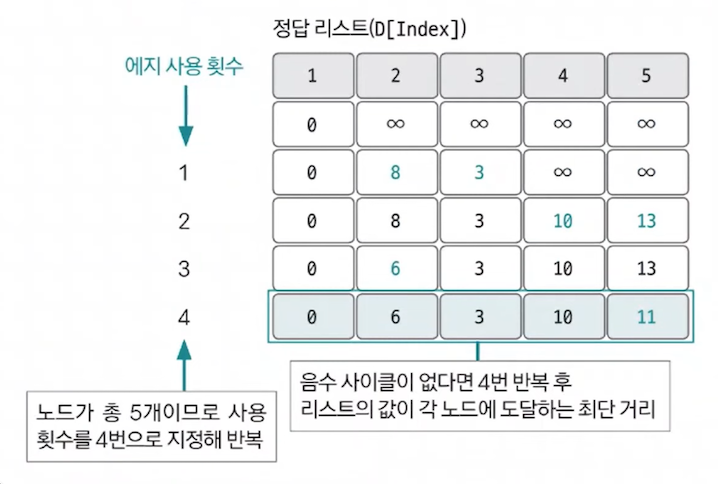
음수 사이클이 없을 때 최대 엣지 갯수가 나오려면 사향 트리 형태에서 양 도착 노드를 선택해야 한다.

• 음수 사이클이 없을 때 N - 1번 엣지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 리스트가 완성된다. 이렇게 완성 후 마지막으로 이 그래프에 음수 사이클이 존재하는지 확인해야 한다.

3. 음수 사이클 유무 확인하기

• 음수 사이클 유무를 확인하기 위해 모든 엣지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하는지 확인한다. 만약 업데이트되는 노드가 있다면 음수 사이클이 있다는 뜻 이되고, 2단계에서 도출한 정답 리스트가 무의미하고 최단 거리를 찾을 수 없는 그래프라는 뜻이 된다. 음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하므로 최단 거리를 구할 수 없다.

---

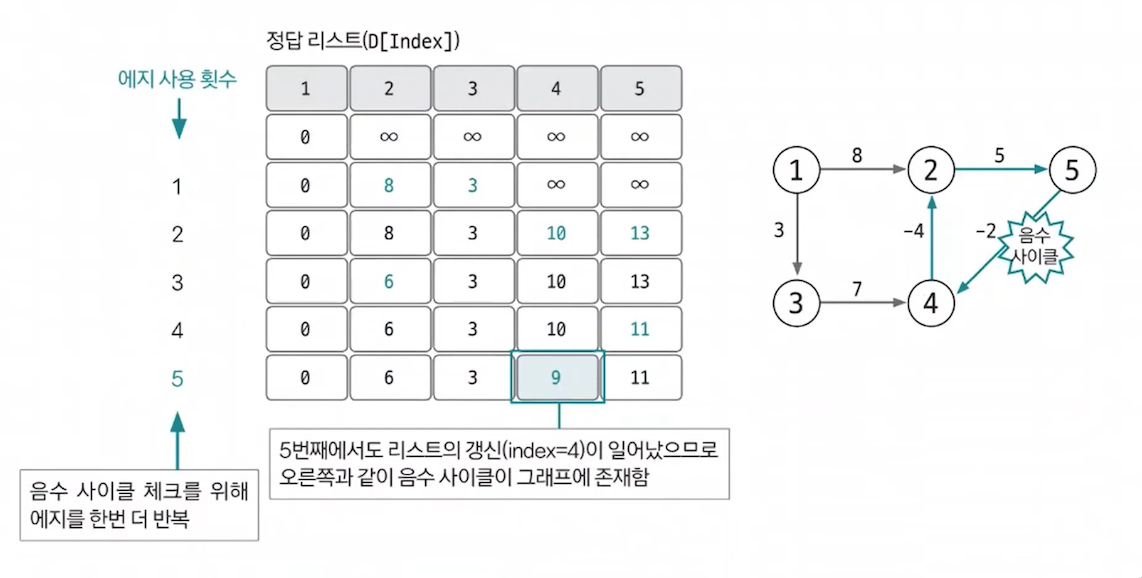
결론

1. 최단거리 N - 1 엣지로 업데이트
2. 이후 한 번 더 업데이트 시도해서 업데이트가 된다면 최단거리를 구할 수 없고, 음수 사이클이 존재한다는 것을 판별할 수 있다.

→실제 코테에서도 벨만-포드 알고리즘을 사용해 최단 거리를 구하는 문제보다 음수 사이클을 판별하는 문제가 더 빈번하게 출제된다. 따라서 마지막에 한 번 더 모든 엣지를 사용해 업데이트되는 노드가 존재하는지 확인해야 한다.

---

출처 - 하루코딩