1. 자료구조와 알고리즘의 이해

이 내용은 윤성우의 열혈 자료구조를 학습한 내용입니다.

1. 자료구조(Data Structure)에 대한 기본적인 이해

1-1. 자료구조란 무엇인가?

프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다.

• 데이터의 표현 ⊃ 데이터의 저장
• ‘데이터의 저장’을 담당하는 것이 바로 자료구조이다.

🚩 자료구조는 ‘데이터의 표현 및 저장방법’을 뜻한다.

🔻 자료구조의 분류

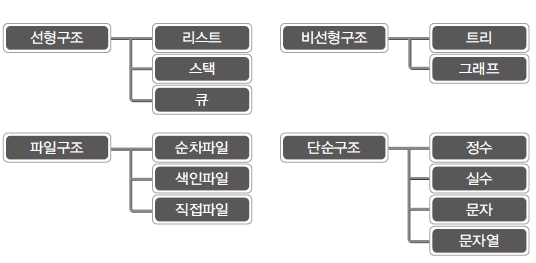
• 파일도 데이터를 저장하는 도구이기 때문에 파일의 구조도 자료구조에 포함이 된다.

• 선형구조(linear)
  • 데이터를 선의 형태로 나란히 혹은 일렬로 저장하는 방식
• 비선형구조
  • 데이터를 나란히 저장하지 않는 구조

1-2. 자료구조와 알고리즘

알고리즘은 자료구조에 의존적이다.

• 자료구조: 데이터의 표현 및 저장방법
• 알고리즘: 표현 및 저장된 데이터를 대상으로 하는 ‘문제의 해결 방법’을 뜻한다.

2. 알고리즘의 성능분석 방법

2-1. 시간 복잡도와 공간 복잡도

• 시간 복잡도(Time Complexity)
  • 알고리즘의 수행시간
• 공간 복잡도(Space Complexity)
  • 메모리 사용량

일반적으로 알고리즘을 평가할 때는 메모리의 사용량보다 실행속도에 초점을 둔다.

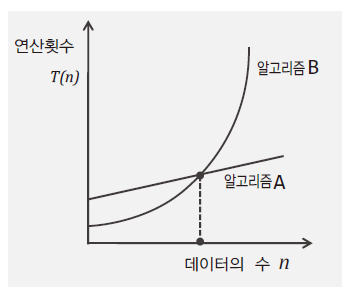
🔻 시간 복잡도의 평가 방법: 연산의 횟수

• 중심이 되는 특정 연산의 횟수를 세어서 평가
• 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성한다.
  • 식을 구성하면 데이터 수의 변화에 따른 연산횟수의 변화 정도를 한눈에 파악할 수 있다.(비교 용이)

2-2. 순차 탐색 알고리즘과 시간 복잡도

• 순차 탐색 알고리즘(Linear Search)
  • 알고리즘에 사용된 연산자는 다음과 같다. <, ++, ==
    • 이 중 동등(==) 연산자를 적게 수행하는 탐색 알고리즘이 좋은 탐색 알고리즘이다. (다른 연산은 의존적이다.)
    • 따라서 == 연산 횟수를 대상으로 시간 복잡도를 분석하면 된다.

     for(i=0; i<len; i++)
     {
    		 if(ar[i] == target)
    				 return i; // 찾은 대상의 인덱스 값 반환
     }

일반적인 알고리즘의 평가에는 ‘최악의 경우(worst case)’를 선택한다.

• 다만 ‘평균적인 경우(average case)’를 계산할 수 있다면 최적이지만 보통 계산이 어렵기에 사용하지 않는다.

✔️ 순차 탐색 알고리즘의 시간 복잡도

• 최악: $T(n)=n$
• 평균: $T(n)= n ×\frac{1}{2}\ +\ \frac{n}{2}×\frac{1}{2}=\frac{3}{4}n$
  • 탐색 대상이 배열에 존재하지 않을 확률을 50 %라고 가정했을 때, 앞 부분(n)은 탐색대상이 존재하지 않을 경우 연산횟수, 뒷 부분(n/2)은 존재하는 연산횟수(근사값)이다.
  • 뒷 부분은 실제로는 (n + 1)/2 이다.
    ⇒ 모든 것은 가정하에 진행됐으므로 신뢰성이 높은 알고리즘은 아니다.

2-3. 이진 탐색 알고리즘

이진 탐색을 사용하기 위해서는 배열에 저장된 데이터는 정렬되어 있어야 한다.

• 탐색 시도 과정
  1. 시작, 끝 인덱스를 합하여 2로 나눈다.
  2. 해당 인덱스(mid)에 해당하는 배열 값이 target인지 확인한다.
     • 맞다면 인덱스(mid)를 반환
     • 다르다면 대소 비교(정렬됨)를 통해 범위를 줄인다.

✔️ 이진 탐색 알고리즘의 탐색 범위 감소 형태

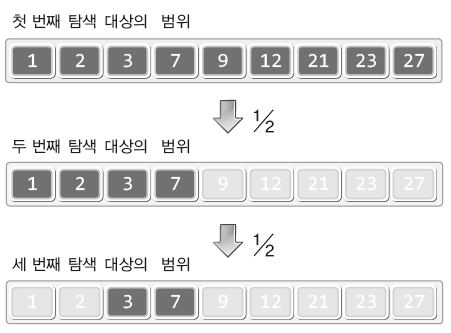
• 이진 탐색의 매 과정마다 탐색의 대상을 반씩 줄여나가기 때문에 순차 탐색보다 좋은 성능을 보인다.

🔻 구현

• 종료조건: first > last → 탐색 실패
  • 탐색의 시작 인덱스: first
  • 탐색의 마지막 인덱스: last
  • first == last
    • 중간값인 mid는 first와 last 같은 값이며, 아직 탐색하지 못한 대상임을 의미한다.

    while(first <= last)
    {
    		// 이진 탐색 알고리즘의 진행
    }

• 알고리즘의 진행

    mid = (first+last) / 2; // 탐색 대상의 중앙을 찾는다.
    if(target == ar[mid]) // 중앙에 저장된 것이 타겟이라면
    {
    	 return mid; // 탐색 완료
    }
    else // 타겟이 아니라면 탐색 대상을 반으로 줄인다.
    {
    	 if(target < ar[mid])
    			 last = mid-1; // -1
    	 else
    				first = mid+1; // +1
    }

✅ 왜 -1, +1을 추가할까?

• ar[mid] 는 타겟이 아니라는 것을 이미 확인했으므로 범위에 포함할 필요가 없다.
• 추가하지 않는다면, first <= mid <=last가 항상 성립한다.
  • 만약 탐색 대상이 존재하지 않는 경우, while 문을 벗어날 수 없다.(first <= last)

✔️ 이진 탐색 알고리즘의 시간복잡도

• 핵심 연산: == 연산자(타겟 적중)
• 최악: $T(n)=log_2n$
  • $T(n) = k + 1$; 최악의 경우 n이 1이 될 때까지 2로 나눈 횟수 k와 탐색 실패 1번
  • $n×(\frac{1}{2})^k = 1$

2-4. 빅-오 표기법(Big-Oh Notation)

빅-오는 함수 T(n) 에서 가장 영향력이 큰 부분이 어딘가를 따지는 것이다.

• T(n) 이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅-오가 된다.
  • $T(n)=a_mn^m+a_{m-1}n^{m-1}+a_1n^1+a_0\ →\ O(n^m)$

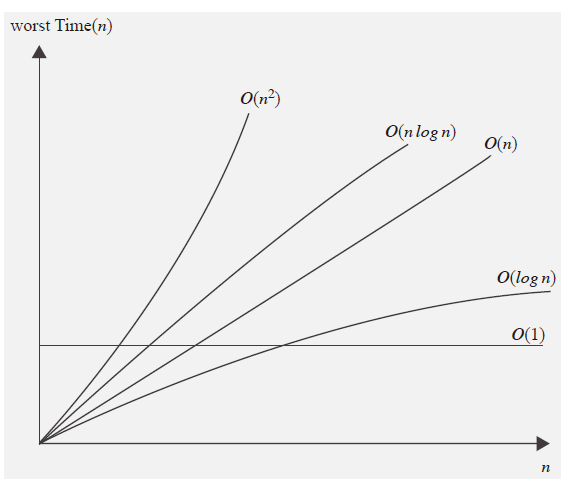
✔️ 대표적인 빅-오

• 성능 대소 비교 $O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)$
  • O(logn): O(n)에 비해서 성능이 월등하다.(n이 커질수록)
  • O(nlogn): 데이터의 수가 n배 늘 때, 연산횟수는 n배를 조금 넘게 증가한다.
  • O(n^2), O(n^3): 2중, 3중 중첩 반복문; 알고리즘 디자인에서 바람직하지는 않다.

✅ 빅-오 구하기

• $3n+2 → O(n)$
• $7n^3+3n^2+2 → O(n^3)$
• $2^n+n^2 → O(2^n)$
• $n+logn → O(n)$
• $n+nlogn → O(nlogn)$
• $2^n+n^3 → O(2^n)$

참고: 윤성우의 열혈 자료구조