이 내용은 윤성우의 열혈 자료구조를 학습한 내용입니다.1. 함수의 재귀적 호출의 이해
1-1. 재귀함수의 기본적인 이해
재귀함수란 함수 내에서 자기 자신을 다시 호출하는 함수를 의미한다.
- 재귀함수의 흐름
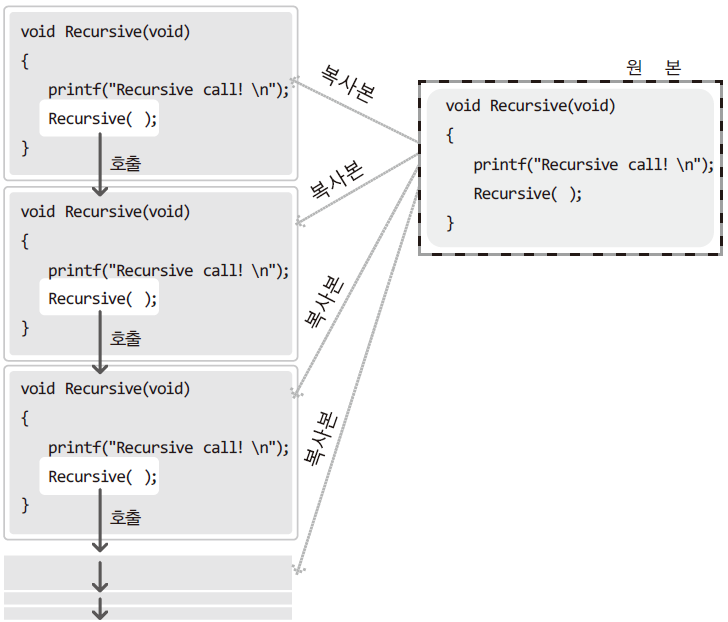
- 원본
Recursive함수의 복사본이 만들어져서 복사본이 실행되는 구조로 재귀함수가 호출된다. - 실제로 함수를 구성하는 명령문은 CPU로 이동이 되어서(복사가 되어서) 실행된다.
- 원본
1-2. 재귀함수의 디자인 사례
🚩 재귀함수는 반복되는 구조(패턴)를 찾는 것이 중요하다.
✔️ 수학적 표현
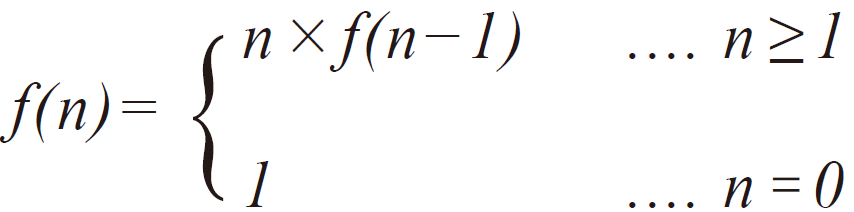
f(0)에 해당하는0!이 재귀함수의 탈출조건이 된다.
#include <stdio.h>
int Factorial(int n)
{
if(n==0) // 탈출조건
return 1;
else // 재귀함수 호출
return n * Factorial(n-1);
}2. 재귀의 활용
2-1. 피보나치 수열: Fibonacci Sequence
이전의 두 수를 더해서 현재 수를 만들어가는 수열
수열의 n번째 값=수열의 n-1번째 값+수열의 n-2번째 값
✔️ 수학적 표현
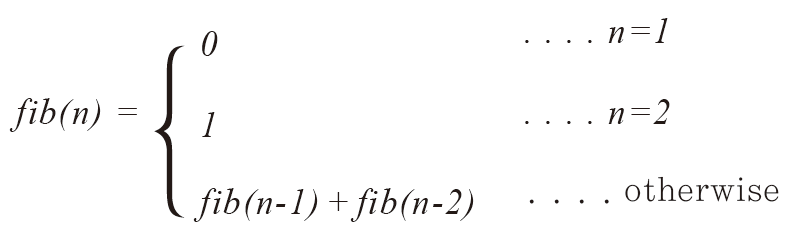
#include <stdio.h>
int Fibo(int n)
{
if(n==1)
return 0;
else if(n==2)
return 1;
else
return Fibo(n-1)+Fibo(n-2);
}- 함수의 호출순서
- 만약,
Fibo(7)을 실행했다고 한다면return Fibo(6) + Fibo(5);가 실행된다.- 이때,
+연산자 왼편에 있는 Fibo 함수호출이 완료되어야 비로소 오른편에 있는 Fibo 함수호출이 진행된다.
- 이때,
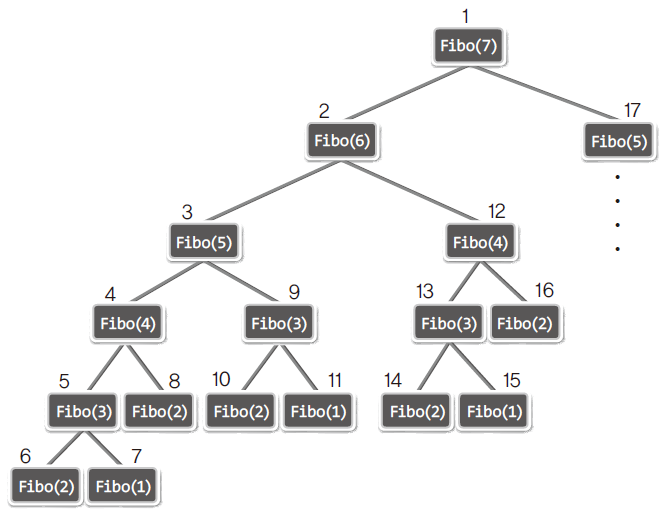
- 만약,
2-2. 이진 탐색 알고리즘의 재귀적 구현
이진 탐색의 두 번째 시도 이후부터는 탐색 대상을 찾을 때까지 동일한 패턴을 반복할 뿐이다.
- 이진 탐색 알고리즘의 반복 패턴
-
탐색 범위의 중앙에 목표 값이 저장되었는지 확인
-
저장되지 않았다면 탐색 범위를 반으로 줄여서 다시 탐색 시작
✅ 종료 조건
- 탐색 대상을 찾았다.
- 탐색 실패:
first > last
-
🔻 구현
- 탈출조건 삽입
int BSearchRecur(int ar[], int first, int last, int target)
{
int mid;
if(first > last)
return -1; // -1의 반환은 탐색의 실패를 의미
}- 반복배턴 삽입
- “탐색 범위의 중앙에 목표 값이 저장되었는지 확인”
int BSearchRecur(int ar[], int first, int last, int target)
{
int mid;
// if(first > last)
// return -1;
mid = (first+last) / 2; // 탐색 대상의 중앙을 찾는다.
if(ar[mid] == target)
return mid; // 탐색된 타겟의 인덱스 값 반환
}- “저장되지 않았다면 탐색 범위를 반으로 줄여서 다시 탐색 시작”
#include <stdio.h>
int BSearchRecur(int ar[], int first, int last, int target)
{
int mid;
// if(first > last)
// return -1;
// mid = (first+last) / 2;
// if(ar[mid] == target)
// return mid;
else if(target < ar[mid])
return BSearchRecur(ar, first, mid-1, target);
else
return BSearchRecur(ar, mid+1, last, target);
}📌 탐색의 범위를 반으로 줄여서 다시 BSearchRecur 함수를 호출하는 것이 핵심이다.
🚩 재귀함수를 구현하기 위해서는 탈출조건과 반복패턴을 잘 정리하는 것이 중요하다.
3. 하노이 타워
‘하나의 막대에 쌓여 있는 원반을 다른 하나의 원반에 그대로 옮기는 방법’에 관한 것이다.
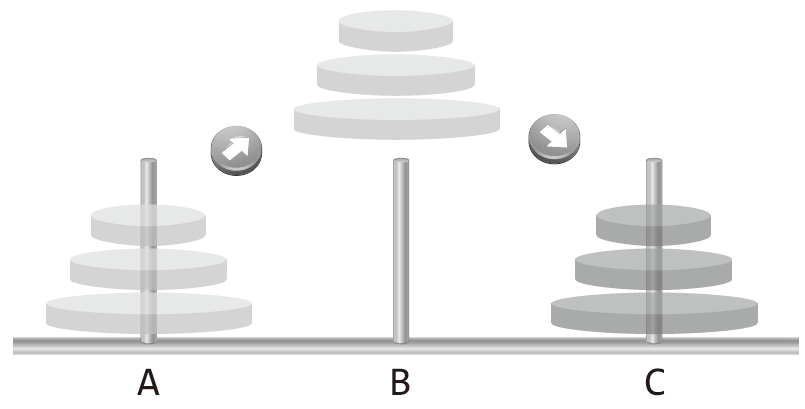
- 제약사항
- 원반은 한 번에 하나씩만 옮길 수 있다.
- 옮기는 과정에서 작은 원반의 위에 큰 원반이 올려져서는 안된다.
→ 하노이 타워 문제는 위 제약사항을 만족하면서 A의 모든 원반을 C로 옮기는 문제이다.
3-1. 하노이 타워의 반복패턴
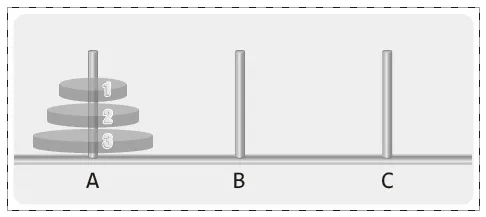
- A의 세 원반을 C로 옮기기 위해서는 원반 3을 C로 옮겨야 한다.(제약 사항)
- 이를 위해서는 원반 1과 2를 우선 원반 B로 옮겨야 한다.
위와 같은 패턴을 확장시켜 일반화하게 된다면 다음과 같다.
- 작은 원반
n-1개(맨 아래 원반을 제외한 나머지 원반)를 A에서 B로 이동 - 큰 원반(맨 아래 원반) 1개를 A에서 C로 이동
- 작은 원반(위의 1단계에서 옮겨진 원반)
n-1개를 B에서 C로 이동
⇒ 원반 n 개를 이동하는 문제는 원반 n-1 개를 이동하는 문제로 세분화되고, 결국 원반 1개를 이동하는 문제로 세분화된다.
3-2. 하노이 타워 문제의 해결
- 기본 골격
// from에 꽂혀있는 num개의 원반을 by를 거쳐서 to로 이동
void HanoiTowerMove(int num, char from, char by, char to)
{
}- 탈출 조건: 이동해야 할 원반의 수가 1개인 경우
void HanoiTowerMove(int num, char from, char by, char to)
{
if(num==1) // 이동할 원반의 수가 1개라면
{
printf("원반1을 %c에서 %c로 이동 \n", from, to);
}
else
{
....
}
}- 반복 패턴
- 작은 원반
n-1개(맨 아래 원반을 제외한 나머지 원반)를 A에서 B로 이동
void HanoiTowerMove(int num, char from, char by, char to)
{
if(num==1) // 이동할 원반의 수가 1개라면
{
printf("원반1을 %c에서 %c로 이동 \n", from, to);
}
else
{
HanoiTowerMove(num-1, from, to, by); // 3단계 중 1단계
}
}- 큰 원반(맨 아래 원반) 1개를 A에서 C로 이동 + 작은 원반(위의 1단계에서 옮겨진 원반)
n-1개를 B에서 C로 이동
void HanoiTowerMove(int num, char from, char by, char to)
{
if(num==1) // 이동할 원반의 수가 1개라면
{
printf("원반1을 %c에서 %c로 이동 \n", from, to);
}
else
{
HanoiTowerMove(num-1, from, to, by); // 3단계 중 1단계
printf("원반%d를 %c에서 %c로 이동 \n", num, from, to); // 2단계
HanoiTowerMove(num-1, by, from, to); // 3단계
}
}참고: 윤성우의 열혈 자료구조
