이 내용은 윤성우의 열혈 자료구조를 학습한 내용입니다.1. 그래프의 이해와 종류
1-1. 그래프의 이해와 종류
그래프는 정점과 간선의 집합이다.
- 정점(vertex): 연결의 대상이 되는 개체 또는 위치
- 간선(edge): 정점 사이의 연결
🔻 그래프의 종류
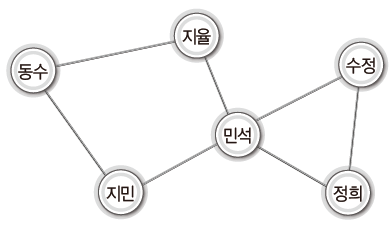
- 무방향 그래프(undirected graph)
-
연결 관계에 있어 방향성이 없는 그래프
-
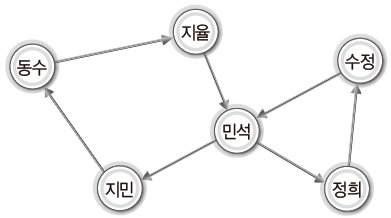
- 방향 그래프(directed graph)
-
간선에 방향정보가 포함된 그래프
-
- 완전 그래프(complete graph)
-
각각의 정점에서 다른 모든 정점을 연결한 그래프
-
방향 그래프의 간선의 수=무방향 그래프의 간선의 수 × 2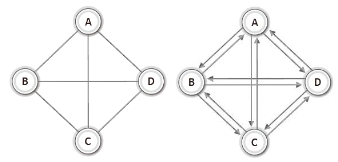
-
1-2. 가중치 그래프와 부분 그래프
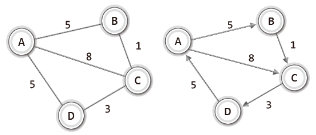
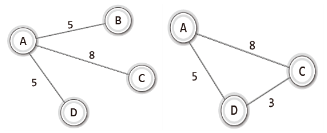
- 가중치 그래프(Weight Graph)
-
간선에 가중치 정보를 두어 구성한 그래프
-
가중치
- 두 정점 사이의 거리 혹은 두 정점을 이동하는데 걸리는 시간 등의 정보가 될 수 있다.
-
- 부분 그래프(Sub Graph)
-
원래의 그래프의 일부 정점 및 간선으로 이뤄진 그래프
-
1-3. 그래프의 집합 표현
🔻 표현
- 그래프
G의 정점 집합:V(G)V(G1) = {A, B, C, D}
- 그래프
G의 간선 집합:E(G)E(G1) = {(A, B), (A, C)}- 무방향 그래프:
(A, B) - 방향 그래프:
<A, B>(정점A가 정점B를 가리킨다.)
1-4. 그래프의 ADT
void GraphInit(ALGraph * pg, int nv);- 그래프의 초기화를 진행한다.
- 두 번째 인자로 정점의 수(
nv)를 전달한다.
void GraphDestroy(ALGraph * pg);- 그래프 초기화 과정에서 할당한 리소스를 반환한다.
void AddEdge(ALGraph * pg, int fromV, int toV);- 매개변수
fromV와toV로 전달된 정점을 연결하는 간선을 그래프에 추가한다.
- 매개변수
void ShowGraphEdgeInfo(ALGraph * pg);- 그래프의 간선정보를 출력한다.
1-5. 그래프를 구현하는 두 가지 방법
✔️ 인접 행렬 기반 그래프(adjacent matrix) : 정방 행렬을 활용
- 정방 행렬: 가로세로의 길이가 같은 행렬 (2차원 배열)
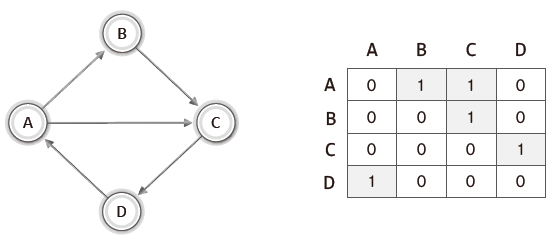
- 정점이
N개면N × N크기의 2차원 배열을 선언한다. 행(A)→열(B)로 향하는 간선의 표시를 위해 [0][1] 인 위치를 1로 표시했다.
✔️ 인접 리스트 기반 그래프(adjacent list): 연결 리스트를 활용
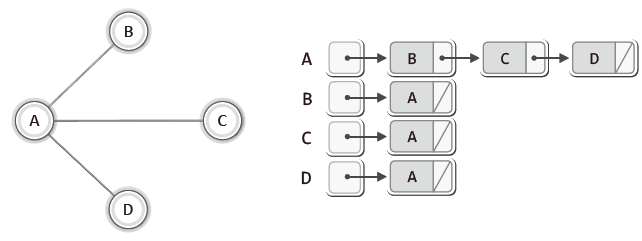
- 각각의 정점은 자신과 연결된 정점의 정보를 담기 위해서 하나의 연결 리스트를 갖는다.
- 각각의 정점에 연결된 간선의 정보는 각각의 연결 리스트에 담는다.
2. 인접 리스트 기반의 그래프 구현
2-1. 헤더파일의 정의
#ifndef __AL_GRAPH__
#define __AL_GRAPH__
// 연결 리스트를 활용한다.
#include "DLinkedList.h"
// 정점의 이름을 상수화
enum {A, B, C, D, E, F, G, H, I, J};
typedef struct _ual
{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
} ALGraph;
// 그래프의 초기화
void GraphInit(ALGraph * pg, int nv);
// 그래프의 리소스 해제
void GraphDestroy(ALGraph * pg);
// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV);
// 간선의 정보 출력
void ShowGraphEdgeInfo(ALGraph * pg);
#endif- 정점/간선의 수 정보와 인접리스트로 간선의 정보를 관리한다.
2-2. 그래프의 구현
무방향 그래프를 기준으로 구현해보자.
- 초기화
// 그래프의 초기화 void GraphInit(ALGraph * pg, int nv) { int i; // 정점의 수에 해당하는 길이의 리스트 배열을 생성한다. pg->adjList = (List*)malloc(sizeof(List)*nv); // 간선 정보를 저장할 리스트 생성 pg->numV = nv; // 정점의 수 nv pg->numE = 0; // 초기의 간선 수는 0개 // 정점의 수만큼 생성된 리스트들을 초기화한다. for(i=0; i<nv; i++) { ListInit(&(pg->adjList[i])); SetSortRule(&(pg->adjList[i]), WhoIsPrecede); // 리스트의 정렬기준을 설정 } }SetSortRule()은 그래프와 연관성이 없지만, 연결 리스트가 요구하므로 적당한 함수를 등록했다.
- 소멸
// 그래프의 리소스 해제 void GraphDestroy(ALGraph * pg) { if(pg->adjList != NULL) free(pg->adjList); // 동적으로 할당된 연결 리스트의 소멸 }
- 간선의 추가
// fromV, toV 연결하는 간선 추가 void AddEdge(ALGraph * pg, int fromV, int toV) { LInsert(&(pg->adjList[fromV]), toV); // 정점 fromV의 연결 리스트에 정점 toV의 정보 추가 LInsert(&(pg->adjList[toV]), fromV); // 정점 toV의 연결 리스트에 정점 fromV의 정보 추가 pg->numE += 1; // 간선 수 증가 }- 헤더파일 기준으로 정점의 이름이 의미하는 바는 상수이다. 그리고 그 값은 0에서부터 시작해서 1씩 증가한다.
- 간선의 정보 출력
// 간선의 정보 출력 void ShowGraphEdgeInfo(ALGraph * pg) { int i; int vx; for(i=0; i<pg->numV; i++) { printf("%c와 연결된 정점: ", i + 65); // ASCII 코드 if(LFirst(&(pg->adjList[i]), &vx)) { printf("%c ", vx + 65); while(LNext(&(pg->adjList[i]), &vx)) printf("%c ", vx + 65); } printf("\n"); } }
3. 그래프의 탐색
그래프의 모든 정점을 탐색하기 위한 알고리즘은 깊이 우선 탐색과 너비 우선 탐색 두 가지가 있다.
3-1. 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)
- 깊이 우선 탐색(DFS: Depth First Search)
-
자신과 연결된 한 정점으로만 탐색한다.
-
탐색할 정점이 없다면, 자신을 탐색한 정점에게 이를 알린다.
- 역으로 되돌아 가면서 탐색할 곳을 찾는다.
-
처음 탐색을 시작한 정점의 위치에서 탐색은 끝난다.
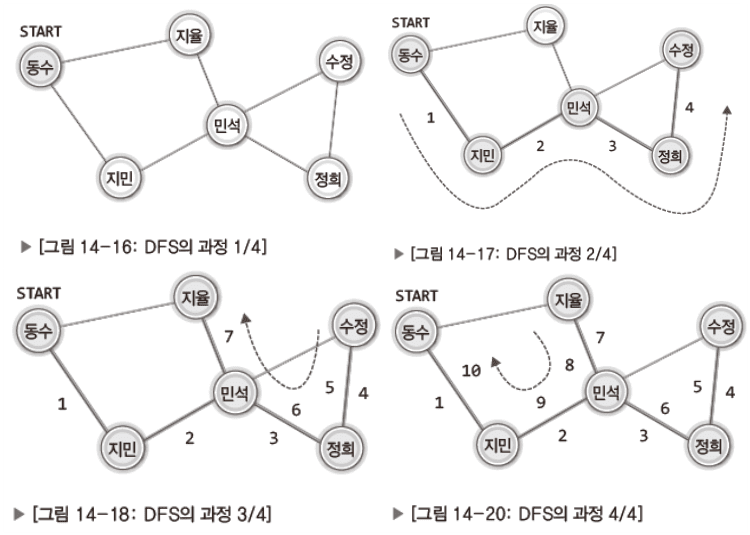
-
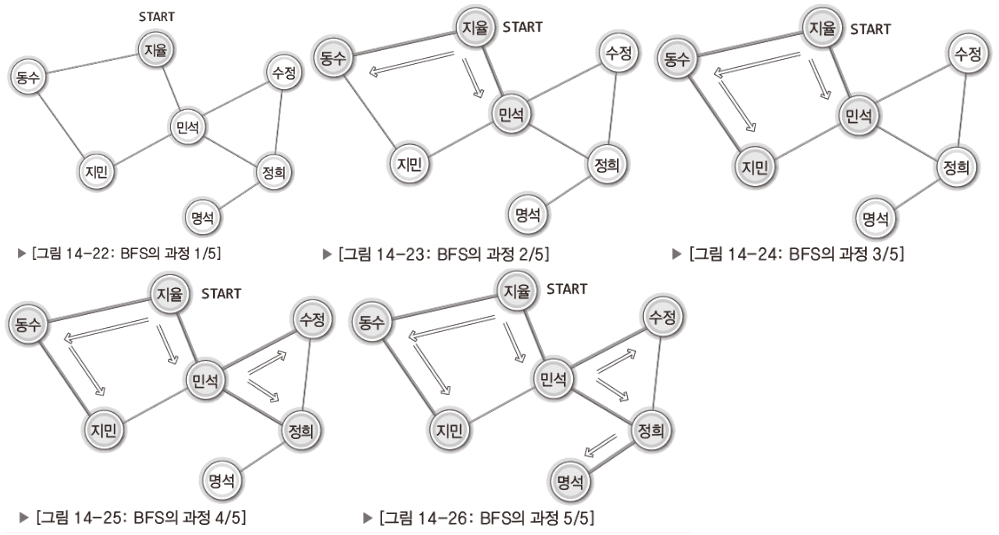
- 너비 우선 탐색(BFS: Breadth First Search)
-
한 정점을 기준으로 자신에게 연결된 모든 정점을 탐색한다.
-
이미 방문한 정점을 제외하고 탐색을 이어 나간다.
-
3-2. 깊이 우선 탐색의 구현 모델
🔻 필요 요소
- 스택: 경로 정보의 추적
- 갔던 길을 되돌아올 때 사용한다.
- 방문한 정점을 떠날 때에는 떠나는 정점의 정보가 스택에 저장된다.
- 배열: 방문 정보의 기록
- 헤더 파일
#ifndef __AL_GRAPH_DFS__ #define __AL_GRAPH_DFS__ // 연결 리스트를 활용한다. #include "DLinkedList.h" // 정점 이름들의 상수화 enum {A, B, C, D, E, F, G, H, I, J}; typedef struct _ual { int numV; // 정점의 수 int numE; // 간선의 수 List * adjList; // 간선의 정보 int * visitInfo; } ALGraph; // 그래프의 초기화 void GraphInit(ALGraph * pg, int nv); // 그래프의 리소스 해제 void GraphDestroy(ALGraph * pg); // 간선의 추가 void AddEdge(ALGraph * pg, int fromV, int toV); // 간선의 정보 출력 void ShowGraphEdgeInfo(ALGraph * pg); // 정점의 모든 정점 정보 출력: DFS 기반 void DFShowGraphVertex(ALGraph * pg, int startV); #endif- 구조체에
visitInfo라는 멤버가 추가 되었다.-
탐색이 진행된 정점의 정보를 담는 배열
// 정점의 수를 길이로 하여 배열을 할당 pg->visitInfo= (int *)malloc(sizeof(int) * pg->numV); // 배열의 모든 요소를 0으로 초기화 memset(pg->visitInfo, 0, sizeof(int) * pg->numV);
-
- 구조체에
- 초기화와 소멸
- 초기화
void GraphInit(ALGraph * pg, int nv) // 그래프의 초기화 { .... // 정점의 수를 길이로 하여 배열을 할당 pg->visitInfo= (int *)malloc(sizeof(int) * pg->numV); // 배열의 모든 요소를 0으로 초기화 memset(pg->visitInfo, 0, sizeof(int) * pg->numV); } - 소멸
void GraphDestroy(ALGraph * pg) // 그래프의 리소스 해제 { .... // 할당된 배열의 소멸 if(pg->visitInfo != NULL) free(pg->visitInfo); } visitInfo와 관련한 배열 할당과 소멸 코드가 추가되었다.
- 초기화
- 정점의 방문 기록
// 방문한 점의 정보를 기록 및 출력 int VisitVertex(ALGraph * pg, int visitV) { if(pg->visitInfo[visitV] == 0) // visitV에 처음 방문이라면 { pg->visitInfo[visitV] = 1; // 방문 기록 printf("%c ", visitV + 65); return TRUE; // 방문 성공 } return FALSE; // 이미 방문한 정점이라면 FALSE 반환 }DFShowGraphVertex함수의 구현에 필요한,DFShowGraphVertex함수 내에서 호출이 되는 함수
- 모든 정점의 정보 출력: DFS
// 그래프의 정점 정보 출력 void DFShowGraphVertex(ALGraph * pg, int startV) { Stack stack; int visitV = startV; int nextV; StackInit(&stack); // 스택 초기화 VisitVertex(pg, visitV); // 시작 정점 방문 SPush(&stack, visitV); // 시작 정점의 정보를 스택에 저장 while(LFirst(&(pg->adjList[visitV]), &nextV) == TRUE) { int visitFlag = FALSE; if(VisitVertex(pg, nextV) == TRUE) // 방문 성공 { SPush(&stack, visitV); // visitV에 담긴 정점의 정보를 push visitV = nextV; // 다음 정점으로 이동 visitFlag = TRUE; } else // 방문 실패 시 연결된 다른 정점들을 찾는다. { while(LNext(&(pg->adjList[visitV]), &nextV) == TRUE) { if(VisitVertex(pg, nextV) == TRUE) { SPush(&stack, visitV); visitV = nextV; visitFlag = TRUE; break; } } } if(visitFlag == FALSE) // 추가로 방문한 정점이 없었다면 { // 스택이 비면 탐색의 시작점으로 돌아온 것 if(SIsEmpty(&stack) == TRUE) break; else visitV = SPop(&stack); // 이전 탐색 정점을 살펴봄 } } // 이후의 탐색을 위해 탐색 정보 초기화 memset(pg->visitInfo, 0, sizeof(int) * pg->numV); }
3-3. 너비 우선 탐색의 구현 모델
🔻 필요 요소
- 큐: 방문 차례의 기록
- 배열: 방문 정보의 기록
- 헤더파일
#ifndef __AL_GRAPH_BFS__ #define __AL_GRAPH_BFS__ // 연결 리스트를 활용한다. #include "DLinkedList.h" // 정점 이름들의 상수화 enum {A, B, C, D, E, F, G, H, I, J}; typedef struct _ual { int numV; // 정점의 수 int numE; // 간선의 수 List * adjList; // 간선의 정보 int * visitInfo; } ALGraph; // 그래프의 초기화 void GraphInit(ALGraph * pg, int nv); // 그래프의 리소스 해제 void GraphDestroy(ALGraph * pg); // 간선의 추가 void AddEdge(ALGraph * pg, int fromV, int toV); // 간선의 정보 출력 void ShowGraphEdgeInfo(ALGraph * pg); // 정점의 정보 출력: BFS 기반 void BFShowGraphVertex(ALGraph * pg, int startV); #endif- DFS 구현인 경우와 비교하여 정점 출력 함수를 제외하고 다른 것은 없다.
- 모든 정점의 정보 출력: BFS
void BFShowGraphVertex(ALGraph * pg, int startV) { Queue queue; int visitV = startV; int nextV; QueueInit(&queue); VisitVertex(pg, visitV); // 시작 정점을 탐색한다. // visitV와 연결된 모든 정점에 방문 while(LFirst(&(pg->adjList[visitV]), &nextV) == TRUE) { if(VisitVertex(pg, nextV) == TRUE) Enqueue(&queue, nextV); // nextV에 방문했으니 큐에 저장 while(LNext(&(pg->adjList[visitV]), &nextV) == TRUE) { if(VisitVertex(pg, nextV) == TRUE) Enqueue(&queue, nextV); } if(QIsEmpty(&queue) == TRUE) // 큐가 비면 BFS 종료 break; else visitV = Dequeue(&queue); // 큐에서 하나 꺼내어 while문 반복 } // 이후의 탐색을 위해 탐색 정보 초기화 memset(pg->visitInfo, 0, sizeof(int) * pg->numV); }
4. 최소 비용 신장 트리
4-1. 사이클을 형성하지 않는 그래프
- 경로: 두 개의 정점을 잇는 간선을 순서대로 나열한 것
- 단순 경로(simple path)
- 동일한 간선을 중복하여 포함하지 않는 경로(
B-A-C-D)
- 동일한 간선을 중복하여 포함하지 않는 경로(
- 단순 경로(simple path)
- 사이클(cycle)
- 단순 경로이면서 시작과 끝이 같은 경로 (
A-B-C-A)
- 단순 경로이면서 시작과 끝이 같은 경로 (
✔️ 신장 트리(spanning tree)
- 사이클을 형성하지 않는 그래프
- 이는 그래프이자 트리이다.
- 가중치 그래프와 방향 그래프를 대상으로도 신장 트리를 구성할 수 있다.
4-2. 최소 비용 신장 트리의 이해와 적용
🔻 신장 트리의 특징
- 그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다.
- 그래프 내에서 사이클을 형성하지 않는다.
✔️ 최소 비용 신장 트리(Minimum cost Spanning Tree)/최소 신장 트리(MST)
- 신장 트리의 모든 간선의 가중치 합이 최소인 그래프
4-3. 최소 비용 신장 트리의 구성을 위한 크루스칼 알고리즘
최소 비용 신장 트리의 구성에 사용되는 대표적인 알고리즘은 두 가지이다.
- 크루스칼(Kruskal) 알고리즘
- 가중치를 기준으로 간선을 정렬한 후에 MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식
- 프림(Prim) 알고리즘
- 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식
🔻 과정1 (오름차순)
-
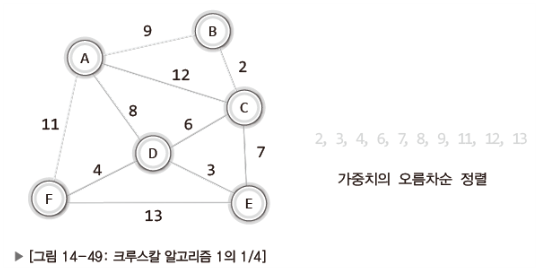
가중치를 기준으로 간선을 오름차순으로 정렬한다.
-
낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가한다.
- 단, 사이클을 형성하는 간선은 추가하지 않는다.
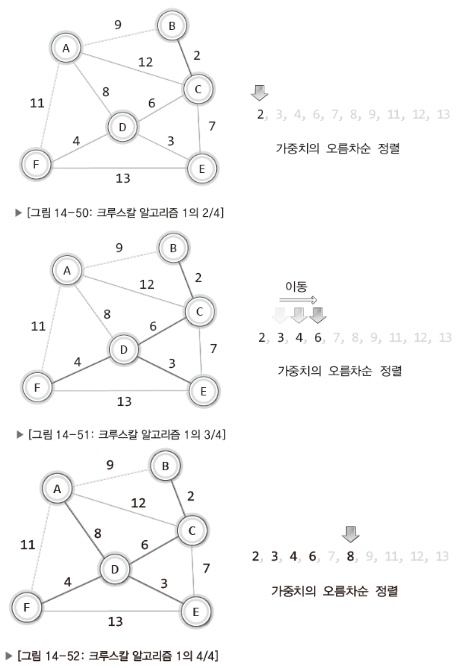
-
간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
🔻 과정2 (내림차순)
-
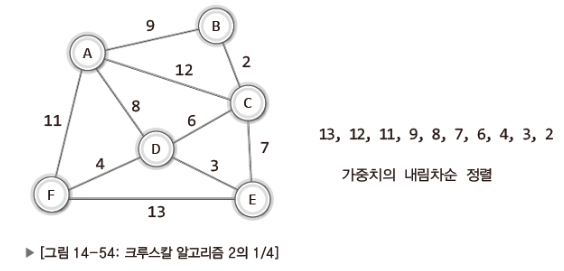
가중치를 기준으로 간선을 내림차순으로 정렬한다.
-
높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거한다.
- 단, 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않는다.
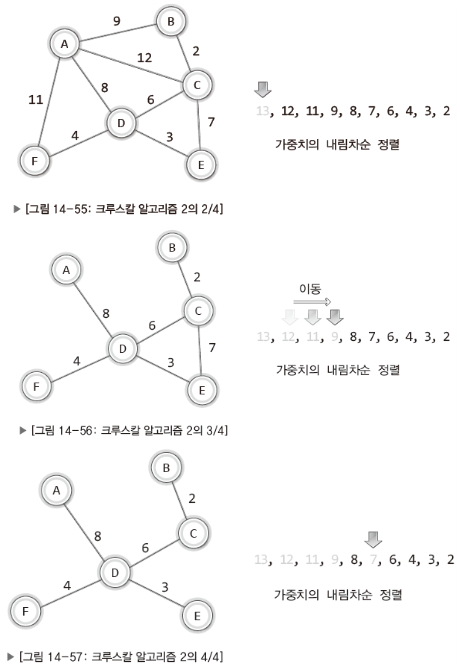
-
간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
4-4. 크루스칼 알고리즘의 구현을 위한 계획
가중치를 기준으로 간선을 내림차순으로 정렬한 다음 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거하는 방식으로 구현하고자 한다.
✔️ 구현에 사용할 도구
- 연결 리스트
- 배열 기반 스택
- 깊이 우선 탐색을 포함하는 그래프 → 크루스칼 알고리즘 기반의 그래프로 변경
📝 간선 삭제 시 이 간선에 의해 연결된 두 정점을 연결하는 대체 경로가 있는가?
- DFS 알고리즘 활용
📝 가중치를 기준으로 간선을 어떻게 정렬할 것인가?
- 우선순위 큐를 활용
- 헤더 파일(ALEdege.h)
#ifndef __AL_EDGE__ #define __AL_EDGE__ typedef struct _edge { int v1; // 간선이 연결하는 첫 번째 정점 int v2; // 간선이 연결하는 두 번째 정점 int weight; // 간선의 가중치 } Edge; #endif- 간선의 가중치 정보를 저장하는 구조체
- 가중치 기반의 정렬을 진행하기 위해 구현한다.
- 헤더 파일(ALGraphKruskal.h)
#ifndef __AL_GRAPH_KRUSKAL__ #define __AL_GRAPH_KRUSKAL__ #include "DLinkedList.h" #include "PriorityQueue.h" #include "ALEdge.h" enum {A, B, C, D, E, F, G, H, I, J}; typedef struct _ual { int numV; int numE; List * adjList; int * visitInfo; PQueue pqueue; // 간선의 가중치 정보 저장 } ALGraph; // 이전 함수의 정의와 차이가 있음 void GraphInit(ALGraph * pg, int nv); // 이전 함수와 동일 void GraphDestroy(ALGraph * pg); // 이전 함수의 선언 및 정의와 차이가 있음 void AddEdge(ALGraph * pg, int fromV, int toV, int weight); // 이전과 동일 void ShowGraphEdgeInfo(ALGraph * pg); // 이전과 동일 void DFShowGraphVertex(ALGraph * pg, int startV); void ConKruskalMST(ALGraph * pg); // 최소 비용 신장 트리의 구성 void ShowGraphEdgeWeightInfo(ALGraph * pg); // 가중치 정보 출력 #endif- 우선순위 큐가 그래프의 멤버로 추가되었다.
- 가중치 정보를 나타내는 구조체인 Edge의 변수를 저장한다.
- 우선순위 큐가 그래프의 멤버로 추가되었다.
- 초기화
void GraphInit(ALGraph * pg, int nv) { .... // 우선순위 큐의 초기화 PQueueInit(&(pg->pqueue), PQWeightComp); }
- 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV, int weight) { Edge edge = {fromV, toV, weight}; // 간선의 가중치 정보를 담음 LInsert(&(pg->adjList[fromV]), toV); LInsert(&(pg->adjList[toV]), fromV); pg->numE += 1; // 간선의 가중치 정보를 우선순위 큐에 저장 PEnqueue(&(pg->pqueue), edge); }
- MST 구성
// 크루스칼 알고리즘 기반 MST의 구성 void ConKruskalMST(ALGraph * pg) { Edge recvEdge[20]; // 복원할 간선의 정보 저장 Edge edge; int eidx = 0; int i; // MST를 형성할 때까지 while문을 반복 while(pg->numE+1 > pg->numV) // MST 간선의 수 + 1 == 정점의 수 { // 우선순위 큐에서 가중치가 제일 높은 간선의 정보를 꺼냄 edge = PDequeue(&(pg->pqueue)); RemoveEdge(pg, edge.v1, edge.v2); // 간선 제거 // 간선을 삭제해도 두 정점을 연결하는 경로가 있는지 확인 if(!IsConnVertex(pg, edge.v1, edge.v2)) { RecoverEdge(pg, edge.v1, edge.v2, edge.weight); // 없다면 복원 recvEdge[eidx++] = edge; // 복원한 간선의 정보를 별도로 저장 } } // 우선순위 큐에서 삭제된 간선의 정보를 회복 for(i=0; i<eidx; i++) PEnqueue(&(pg->pqueue), recvEdge[i]); }RemoveEdge: 그래프에서 간선을 삭제한다.IsConnVertex: 두 정점이 연결되어 있는지 확인한다.RecoverEdge: 삭제된 간선을 다시 삽입한다.- 복원한 간선의 정보를 별도로 저장하는 이유
- 우선순위 큐에 다시 넣으면 해당 간선 정보를
dequeue과정에서 다시 꺼냄
- 우선순위 큐에 다시 넣으면 해당 간선 정보를
- 간선의 가중치 정보 출력
// 간선의 가중치 정보 출력 void ShowGraphEdgeWeightInfo(ALGraph * pg) { PQueue copyPQ = pg->pqueue; Edge edge; while(!PQIsEmpty(©PQ)) { edge = PDequeue(©PQ); printf("(%c-%c), w:%d \n", edge.v1+65, edge.v2+65, edge.weight); } }
✔️ Helper Function
- 간선의 삭제
// 간선의 소멸 void RemoveEdge(ALGraph * pg, int fromV, int toV) { RemoveWayEdge(pg, fromV, toV); RemoveWayEdge(pg, toV, fromV); (pg->numE)--; }// 한쪽 방향의 간선 소멸 void RemoveWayEdge(ALGraph * pg, int fromV, int toV) { int edge; if(LFirst(&(pg->adjList[fromV]), &edge)) { if(edge == toV) { LRemove(&(pg->adjList[fromV])); return; } while(LNext(&(pg->adjList[fromV]), &edge)) { if(edge == toV) { LRemove(&(pg->adjList[fromV])); return; } } } }- 무방향 그래프이므로
RemoveWayEdge를 두 번 호출한다.
- 무방향 그래프이므로
- 간선 복원
void RecoverEdge(ALGraph * pg, int fromV, int toV, int weight) { LInsert(&(pg->adjList[fromV]), toV); LInsert(&(pg->adjList[toV]), fromV); (pg->numE)++; }
- 두 정점의 연결 확인
// 인자로 전달된 두 정점이 연결되면 TRUE, 아니면 FALSE 반환 int IsConnVertex(ALGraph * pg, int v1, int v2) { Stack stack; int visitV = v1; int nextV; StackInit(&stack); VisitVertex(pg, visitV); SPush(&stack, visitV); while(LFirst(&(pg->adjList[visitV]), &nextV) == TRUE) { int visitFlag = FALSE; // 목표를 찾음 if(nextV == v2) { // 반환 전 초기화 진행 memset(pg->visitInfo, 0, sizeof(int) * pg->numV); return TRUE; } if(VisitVertex(pg, nextV) == TRUE) { SPush(&stack, visitV); visitV = nextV; visitFlag = TRUE; } else { while(LNext(&(pg->adjList[visitV]), &nextV) == TRUE) { if(nextV == v2) { memset(pg->visitInfo, 0, sizeof(int) * pg->numV); return TRUE; } if(VisitVertex(pg, nextV) == TRUE) { SPush(&stack, visitV); visitV = nextV; visitFlag = TRUE; break; } } } if(visitFlag == FALSE) { if(SIsEmpty(&stack) == TRUE) break; else visitV = SPop(&stack); } } memset(pg->visitInfo, 0, sizeof(int) * pg->numV); return FALSE; }- DFS의 정점 탐색과 유사한 형태를 가진다.
참고: 윤성우의 열혈 자료구조
