전기화학임피던스 분광법(EIS)

이번 포스트에서는 전기화학 임피던스 분광법(EIS)를 통해 배터리 파라미터(R1,R2)를 구해보겠다.

EIS란?

EIS란 전기화학 시료에 여러 주파수의 교류신호를 주어 나오는 전류, 전압을 이용하여 임피던스(Z)를 뽑아내고 해당 값들을 가지고 시료를 분석하는 방법이다.

임피던스란?

복소평면에 존재하는 저항이라고 보면 된다. 전류와 저항의 위상이 다를 떄 임피던스의 크기는 저항과 위상 진폭의 비 이고, 위상차이가 실수축과 이루는 각이 된다.
따라서 임피던스는 2차원상에 표시 가능하고 배터리에 다양한 주파수의 교류신호를 투입하면 그에따른 여러 점들(임피던스 지점)이 2차원 평면에 찍히게 된다. 이를 나이키스트 선도(Nyquist plot)이라고 한다.

다음은 각 소자별로 임피던스를 나타낸 표이다.

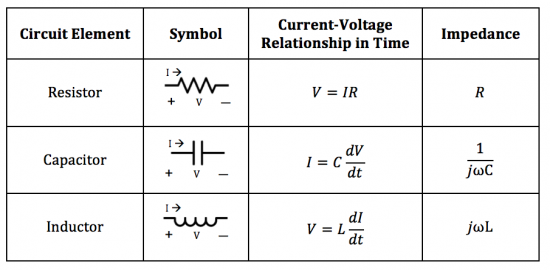
각 소자들이 복잡하게 합쳐있는 등가회로에 대해 전체 임피던스는 해당 소자의 임피던스 값을 직렬, 병렬 합을 해주어서 구할 수 있다.
가령 다음과같은 1차 테브난 등가회로모델의 임피던스를 계산해보자.

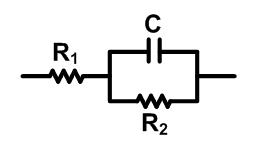
해당 등가회로의 임피던스는 $Z_{R1}+\frac{1}{\frac{1}{Z_{c}}+\frac{1}{Z_{R2}}}$이다.
$Z=Z_{R1}+\frac{1}{\frac{1}{Z_{c}}+\frac{1}{Z_{R2}}}$

$=R1+\frac{1}{iwc+\frac{1}{R2}}$

$=R1+\frac{-iwcR2^2+R2}{w^2C^2R2^2+1}$

여기서 실수부를 x, 허수부를 y좌표로 보면

$(\frac{x-R1}{R2}^2+(\frac{y}{R2})^2)=1$

을 만족한다.
따라서 해당 배터리모델의 nyquist plot은 2차원 평면에서 원을 그리게 되고, x축 절편 각각이 R1+-R2가 된다.

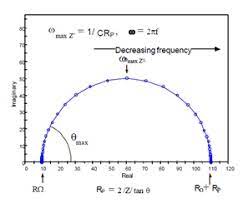
이런 식으로 임의의 등가회로에 대해 nyquist 선도를 구할 수 있다. 그럼 거꾸로 임의의 nyquist선도를 가지고 등가회로 모델을 구할 수 있지 않을까?

이것이 정확히 BMS에서의 EIS의 목적이다.

배터리에 교류신호를 주어서 나온 저항(임피던스,ACIR)를 가지고 배터리 상태를 진단할 수 있다.

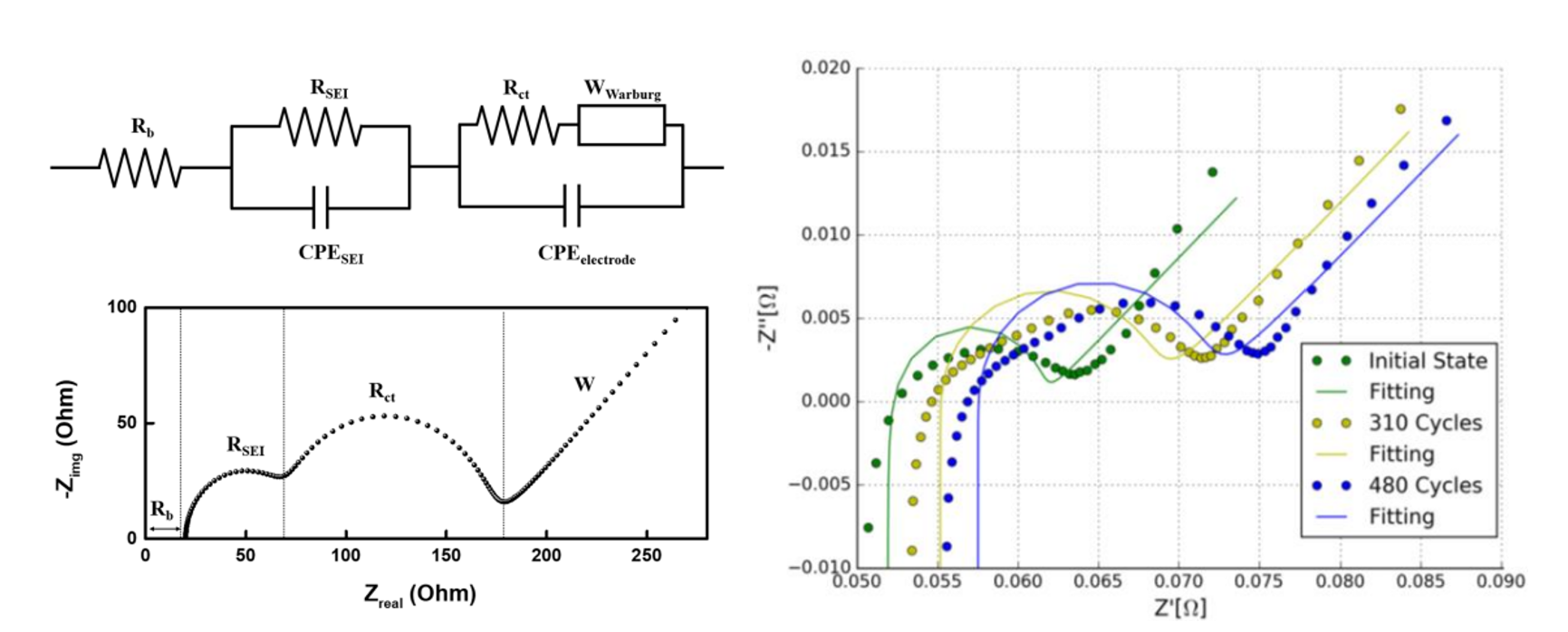
위 사진의 왼쪽은 배터리등가회로의 nyquist선도이고 오른쪽 nyquist선도상의 점선은 실제 배터리의 임피던스이고 실선은 배터리 모델에 맞게 fitting한 곡선이다. 왼쪽의 배터리 모델은 실제 배터리 모델과 경향성이 어느정도 비슷한데 이에맞게 피팅을 해 주어 배터리 내부 파라미터들을 구할 수 있는 것이다.

이 방식이 좋은 이유는 배터리 내부 파라미터를 매우 짧은 시간 안에 구할 수 있기 떄문이다. 실제로 내부저항을 구할 떄 단기간에 생기는 전압변동에 의한 전류변동을 이용해 구하는데 이는 순식간에 변하는 값이기에 내부 화학현상에 의한 비선형적인 항들은 구할 수 없다. 또한 내부저항(Rb)만 정확하게 구할 수 있다.
아무튼 이렇게 EIS를 통해 배터리 모델 파라미터를 구할 수 있고 학계에서 피팅은 zview라는 프로그램을 많이 이용하는 것 같다.

하지만 이를 파이썬으로 구현해보았고, 1차 테브난 회로에 대해서만 진행하였다. 이는 단순히 원적합 문제이며 피팅된 원의 x절편을 뽑아내어 R1,R2를 구할 수 있다. R1은 내부저항으로 배터리 SOH 추출에 이용되는 파라미터이고 R2는 분극저항으로 배터리 SOH추출에 이용되는 파라미터이다.

회사의 배터리검사 db데이터를 이용하여 데이터 분석을 진행하였다.
원 적합 알고리즘같은 경우 선형피팅이기 때문에 비교적 쉽게 구할 수 있었다
원 적합 알고리즘

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rcParams
rcParams['figure.figsize']=5000*(0.0065-0.0045),5000*(0.001+0.0001)
#%%
def return_circle(c): #설명필요..
    x_c = c[1] / 2
    y_c = c[2] / 2
    r = c[0] + x_c ** 2 + y_c ** 2  
    return x_c, y_c, np.sqrt(r) 

def make_circle(c, r):  #중심(c), 반지름(r)을 받아서 원위의 등간격의 256개의 점을 2차원 배열 형식으로 반환하는 함수
    theta = np.linspace(0, 2 * np.pi, 256)  
    x = r * np.cos(theta) 
    y = r * np.sin(theta) 
    return np.vstack((x, y)).T + c
#%% 전처리
#df = pd.read_csv('C:/Users/pmgrow/OneDrive - 피엠/바탕 화면/eis.csv')
df = pd.read_csv('eis.csv')
df=df[df.insp_sq==2302071552191401]
df0=df
df=df[4:18]
df.im=-df.im
plt.scatter(df['re'],df['im'],c=df['hz'])
plt.show()
df=df[['im','re']]


A=df.to_numpy()
ones = np.ones((A.shape[0], 1))
A = np.concatenate((ones, A), axis = 1)
b = A[:,1] ** 2 + A[:,2] ** 2
c = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(b)
x_c, y_c, r_c = return_circle(c)
fitted_circle = make_circle(np.array([x_c, y_c]), r_c)
#%%

plt.plot( fitted_circle[:, 1], fitted_circle[:,0],'r-', label = 'fitted_circle')

plt.scatter(x=df0.re,y=-df0.im)
plt.xlim(0.0045,0.0065)
plt.ylim(-0.0001,0.001)
plt.show()

코드 중간에df=df[4:18]를 넣은 이유는 와버그 임피던스가 강해지는 지점을 무시하기 위해서이다. 원에 최대한 가깝게 나타나는 지점들만 피팅해주었다.

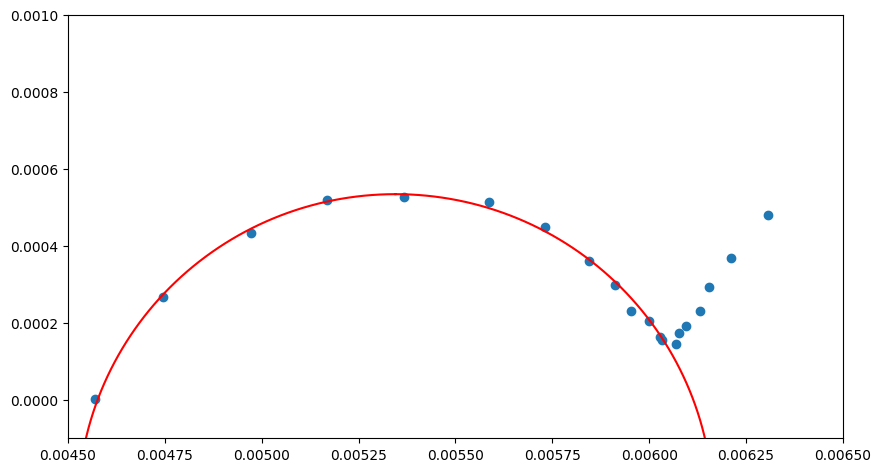
피팅 결과는 다음과 같으며 절편으로 구한 저항값은 실제 검사장비에서 뽑아내는 저항값과 매우 같았는데 정확한 수치는 기억이 안난다.