Introduction
- background
- generative model
- diffusion model
- 1) 이미지가 주어지면 노이지를 줄여가는 diffusion process
- 2) noise 가지고 생성하는 sampling process
- 변분추론?
- Gan 은 둘다 학습인데, difussion은 sampling만 학습. 마르코브 체인 활용
- diffusion model
- Diffusion (2015,NIPS)
- 노이즈를 점차 주입해가고, 그다음에 노이즈를 복구해가는 리버스
- 미리 정의된 가우시안 노이즈 쪼끔씩 주입해나감. 고정해놔서 복원이 쉬운거구나!
- 스텝마다 천번 진행 오호
- objective: vae랑 다른 점은, difussion에서 denoising term이 추가되었다. 오호
- DDPM (2020, NIPS)
- diffusion이랑 비슷한데, loss만 간단하게 해서 성능 향상을 한다.
- mse term이랑 비슷하다.
- 분산을 상수화해서 평균함수만 예측하도록 재구성
- 생략을 하는데, 저게 어떻게 간단하게 생략하는거지??? MSE loss 형태로 simplification을 했다? 우리도 그럼 task를 간단하게 하면 이런식으로 바꿀 수 있는건가?
- generative model
DDIM
- key idea:
- DDPM 원하는 이미지를 생성하기 위해서 천번 스텝을 진행해야하는데 시간이 너무 많이 소요.
- 이미지 질은 똑같지만, 시간은 줄이고 싶다! minor modification으로!
- Approach
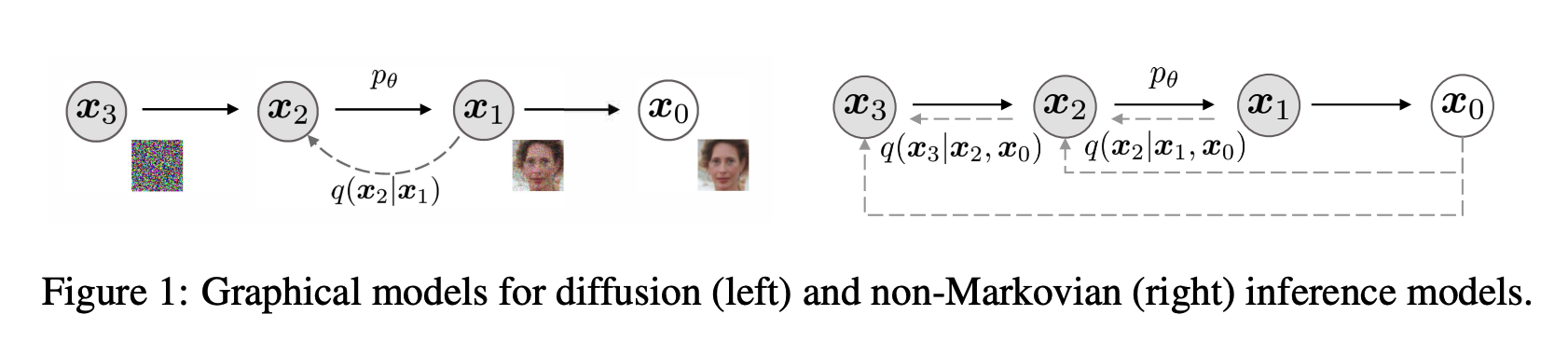
- DDPM: 마르코브 체인
- DDIM: non-마르코브 체인! 이전 스텝에만 의존하는 것이 아니라서 초기화도 같이 보기때문에 non-마르코브다. 오??? 우리도 이렇게 해볼 수 있지 않을까??? 처음 내용을 계속 유지하면서.... 새로운 것만 업데이트 하는 것...!!!!!!!!!!!
- 주변 분포에는 의존하는데 joint에는 영향을 미치 X. 근처에서 유사한 joint 정의하자??????? 1. DDPM의 일반화! 이게 왜 영향 미치고 안미치고 이게 어떤 의미인가????
- 초기 값을 계속 같이 주는 건가! 이게 얼마나 차이가 있는거지..!!!!!!그래도 여전히 전단계를 보긴 본다는 거 아니얌?
- 내가 실제로 알고 싶은 분포하고, 근사하는 분포 차이간을 학습한다. 그래서 대입만 한다. 그래서 joint를 정의를 한건가???
- 시그마 조절해서 DDPM인지, DDIM인지
- sampling
- 노이즈 복원 작업인거겠지?
- 둘차이는 non-markov. 일일이 할 필요가 없어서 가속화 할 수 있다? 모든 스텝을 정의하는게 아니라 첫번째랑 세번째만 한다. 어째서?? 왜???? 갑자기 이게 왜??????
- DDIM 값을 인코딩해서 사용할 수 있다. 확률적으로 이미지 생성하니까, DDIM은 deteministic 하니까 인코딩이 가능하다. 이미 정의되어 있으니까.... 아하아하아하앟아하아하
- gan 보다 vae보다 퀄리티있는 결과물
- 장점은 학습을 안해도 되서 그러는거 아냥?
DDPM은 그 전단계를 기반으로 계속 업데이트를 하기 때문에 새로운 학습이 필요한데, DDIM은 기존에 있던거를 기반으로 다음단계가 얼마나 차이가 있냐 이것만 보기 때문에 모든 스텝 학습할 필요가 없다!!!! 오키도키
실험결과