💡문제
엔토피아는 기억력을 강화하기 위해 게임을 하나 하려고 한다.
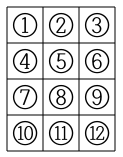
위의 그림과 같이 3×4 칸에 정수가 하나씩 있는 게임판이 하나 있다. 그리고 각 칸을 눌러야 하는 순서가 적혀있는 종이를 엔토피아에게 준다. 그리고 3초 후에 원숭이가 종이를 뻇어간다. 이제 엔토피아는 그걸 잘 기억해서 순서대로 정수를 눌러야 한다.
게임판의 정수를 누를 때는 왼손 엄지나 오른손 엄지를 이용한다. 하나의 칸에 왼손 엄지와 오른손 엄지를 동시에 둘 수도 있다. 그러나, 두 손가락을 동시에 움직일 수는 없다.
엔토피아는 손가락을 움직일 때와 정수를 누를 때마다 체력을 사용한다. 엄지손가락을 어떤 칸에서 다른 칸으로 움직일 때는 두 칸 사이의 거리만큼 체력을 쓴다. 두 칸 사이의 거리는 동서방향 거리 + 남북방향 거리로 정의한다. 어떤 칸을 왼손 엄지로 누를 때는 A의 체력을 사용하고, 오른손 엄지로 누를 때는 B의 체력을 사용한다.
가장 처음에 왼손 엄지는 1번 칸에, 오른손 엄지는 3번 칸에 있다. 정수를 눌러야하는 순서가 입력으로 주어질 때, 엔토피아가 사용하는 최소의 체력을 구해보자.
- 1 ≤ N ≤ 10,000
- 1 ≤ A, B ≤ 100
- 게임판에 존재하는 정수만 순서에 있다.
입력
첫째 줄에 세 정수 N, A, B가 주어진다. 둘째 줄에는 N개의 정수가 주어지는데, 눌러야하는 정수의 순서를 의미한다.
출력
게임을 마치는데 사용한 체력의 최솟값을 출력한다.
예제입력
4 2 3
1 4 6 2예제출력
13📖내가 작성한 Code
import sys
"""
3*4칸에 1~12 번호가 있음
정수 누를때 왼손은 A 체력 사용, 오른손은 B 체력 사용, 이동할 때 체력 사용(동서방향 거리 + 남북뱡향거리)
왼손 엄지 1번칸, 오른손 엄지 3번 칸
"""
INF = 1050001
def find_min_power(array):
n, a, b, *lst = array
dp = {(1, 3): 0}
distance = {
1: '0012123234345',
2: '0101212323434',
3: '0210321432543',
4: '0123012123234',
5: '0212101212323',
6: '0321210321432',
7: '0234123012123',
8: '0323212101212',
9: '0432321210321',
10: '0345234123012',
11: '0434323212101',
12: '0543432321210',
}
for i in lst:
temp = {}
for (l, r), cost in dp.items():
if temp.get((i, r), INF) > (new_cost := cost + a + int(distance[l][i])):
temp[(i, r)] = new_cost
if temp.get((l, i), INF) > (new_cost := cost + b + int(distance[r][i])):
temp[(l, i)] = new_cost
dp = temp
return min(dp.values())
def main():
inputs = list(map(int, sys.stdin.read().split()))
print(find_min_power(inputs))
if __name__ == "__main__":
main()
✍️풀이과정
처음에는 어떻게 풀어야 할까 고민하다가, N이 10000개 뿐이고 상태가 12*12개 뿐이니까 dict로 풀어야겠다고 생각하였다.
O(N) 정도이므로 dict의 오버헤드보다 리스트 전부 탐색하는게 더 부담 될꺼라 생각하고 dict 선택(이후에 리스트로도 풀어보니까 더 늦어짐)
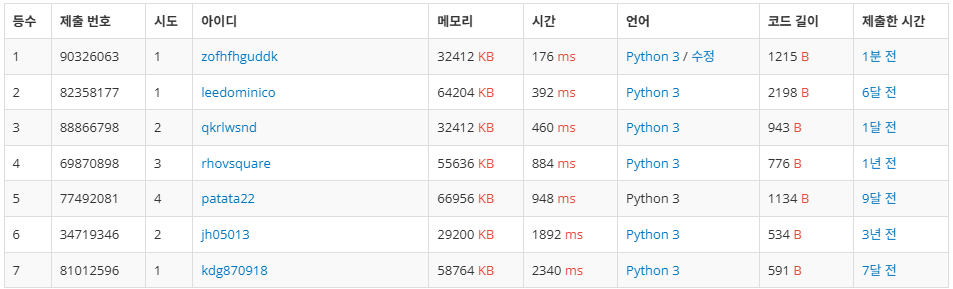
푸는 사람이 없어서 달달하게 1등 먹고 감. 토탐정 랜덤 디펜스로 풀고 있는데 너무 마이너한 문제만 주는 거 같음.
🧠 코드 리뷰
-
거리 계산: 문자열 대신 좌표 기반 맨해튼 거리 계산을 사용하면 가독성과 유지보수성이 향상됩니다.
-
변수 명명: 좀 더 의미 있는 변수명을 사용하면 코드를 읽는 동료나 미래의 자신에게 도움이 됩니다.
-
코드 스타일: PEP8 가이드에 맞추어 일부 변수 및 주석 정리를 고려할 수 있습니다.
🛠️AI 개선 코드
import sys
INF = 1050001
def find_min_power(inputs):
n, left_cost, right_cost, *sequence = inputs
# dp[(l, r)] = 현재 왼손이 l, 오른손이 r에 있을 때까지의 최소 체력 소모량
dp = {(1, 3): 0}
# 3x4 격자: 1번부터 12번 칸의 좌표 (행, 열)
coords = {i: ((i - 1) // 4, (i - 1) % 4) for i in range(1, 13)}
def manhattan(u, v):
r1, c1 = coords[u]
r2, c2 = coords[v]
return abs(r1 - r2) + abs(c1 - c2)
# 각 순서대로 숫자를 누르며 상태 전이
for target in sequence:
new_dp = {}
for (left_pos, right_pos), cost in dp.items():
# 왼손으로 target을 누르는 경우
new_cost_left = cost + left_cost + manhattan(left_pos, target)
state_left = (target, right_pos)
if new_dp.get(state_left, INF) > new_cost_left:
new_dp[state_left] = new_cost_left
# 오른손으로 target을 누르는 경우
new_cost_right = cost + right_cost + manhattan(right_pos, target)
state_right = (left_pos, target)
if new_dp.get(state_right, INF) > new_cost_right:
new_dp[state_right] = new_cost_right
dp = new_dp
return min(dp.values())
def main():
inputs = list(map(int, sys.stdin.read().split()))
print(find_min_power(inputs))
if __name__ == "__main__":
main()
💻결과


