📄문제
이 공간이동 장치는 이동 거리를 급격하게 늘릴 경우 기계에 심각한 결함이 발생하는 단점이 있어서, 이전 작동시기에 k광년을 이동하였을 때는 k-1 , k 혹은 k+1 광년만을 다시 이동할 수 있다. 예를 들어, 이 장치를 처음 작동시킬 경우 -1 , 0 , 1 광년을 이론상 이동할 수 있으나 사실상 음수 혹은 0 거리만큼의 이동은 의미가 없으므로 1 광년을 이동할 수 있으며, 그 다음에는 0 , 1 , 2 광년을 이동할 수 있는 것이다. ( 여기서 다시 2광년을 이동한다면 다음 시기엔 1, 2, 3 광년을 이동할 수 있다. )
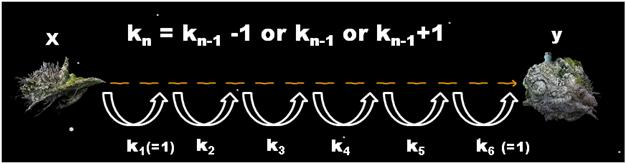
김우현은 공간이동 장치 작동시의 에너지 소모가 크다는 점을 잘 알고 있기 때문에 x지점에서 y지점을 향해 최소한의 작동 횟수로 이동하려 한다. 하지만 y지점에 도착해서도 공간 이동장치의 안전성을 위하여 y지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.
김우현을 위해 x지점부터 정확히 y지점으로 이동하는데 필요한 공간 이동 장치 작동 횟수의 최솟값을 구하는 프로그램을 작성하라.
예제 입력1
3 0 3 1 5 45 50
예제 출력1
3 3 4
🖋️코드
def counting(distance):
i = 0
while i <= distance:
if(distance > i*i and distance <= i*i + i):
return 2*i
elif(distance <=(i + 1)*(i + 1)):
return i*2+1
i+=1
n= int(input())
for _ in range(n):
a,b = map(int,input().split())
print(counting(b-a))🧷(나만 알아듣는) 추가설명
Count(n) Distance Equation 1 1 1**2 2 2 1**2 + 1 3 3~4 2**2 4 5~6 2**2 + 2 5 7~9 3**2 6 10~12 3**2 + 3 7 13~16 4**2 8 17~20 4**2 + 4 패턴을 찾아보자면 이렇다.
짝수일때는 Distance가 (n//2)**2 부터 (n//2)**2+n 까지
홀수일때는 Distance가 (n//2)**2+(n+1) 부터 ((n+1)//2)**2까지
홀수의 n+1인 이유는 짝수가 n까지라서 그렇다.
