AI 기술통계학 추정(estimation) 09-12

alert("april");·2023년 9월 12일

모수 신뢰구간 신뢰수준 오차범위 추정 통계량

AI-PM

목록 보기

11/19

출처 https://www.scalablepath.com/project-management/software-project-estimation

기술 통계 실습

car.xlsx를 이용해서

std(표준편차)

IQR 사분위간 범위(InterQuartile Range)
제3사분위수 제1사분위수
극단값은 최소값 또는 최대값 근처에 있으므로 극단값의 영향이 적음

커널 밀도 추정(Kernel density estimation)
데이터의 밀도를 추정하여 그린 곡선

자주 쓰는 kde
sns.histplot
(x='price', df , kde=True)

표집

모집단과 표본

모집단(population): 연구의 관ㅅ미이 되는 집단 전체
표본(sample): 특정 연구에서 선택된 모집단의 부분 집합
표집(sampling): 모집단에서 표본을 추출하는 절차."표본 추출"이라고도 함
대부분의 경우 집단 전체를 전수조사하기는 어려우므로 무작위로 표본을 추출하여 모집단에 대해 추론

모수(popluation parameter) = 모집단의 특성치

파라미터(parameter): 어떤 시스템의 특성을 나타내는 값
모수: 모집단(population)의 파라미터 -> 모집단의 특성을 나타내는 값
예시:
모집단의 평균(모평균)
모집단의 분산(모분산)
주의!
"표본의 크기"를 "모수"라고 하는 경우도 있으나 잘못된 표현
ex) 국민연금 모수개혁안 (바르게 쓴것)
~~고신용자의 모수 증가~~(틀리게 쓴것) 모수 -> 숫자

통계량(sample statistic)

표본에서 얻어진 수로 계산한 값(통계치)
예시:
표본의 평균 표본평균
표본의 분산 표본분산
주의!!
"모집단의 통계량" 이라는 표현은 없음(통계량은 표본에서 구한 값)
"표본의 모수" 같은 말도 없음(모수는 모집단에서 구한 값)
추론 통계 inferential statistics : 표본 통계량을 일반화하여 모집단에 대해 추론 하는 것

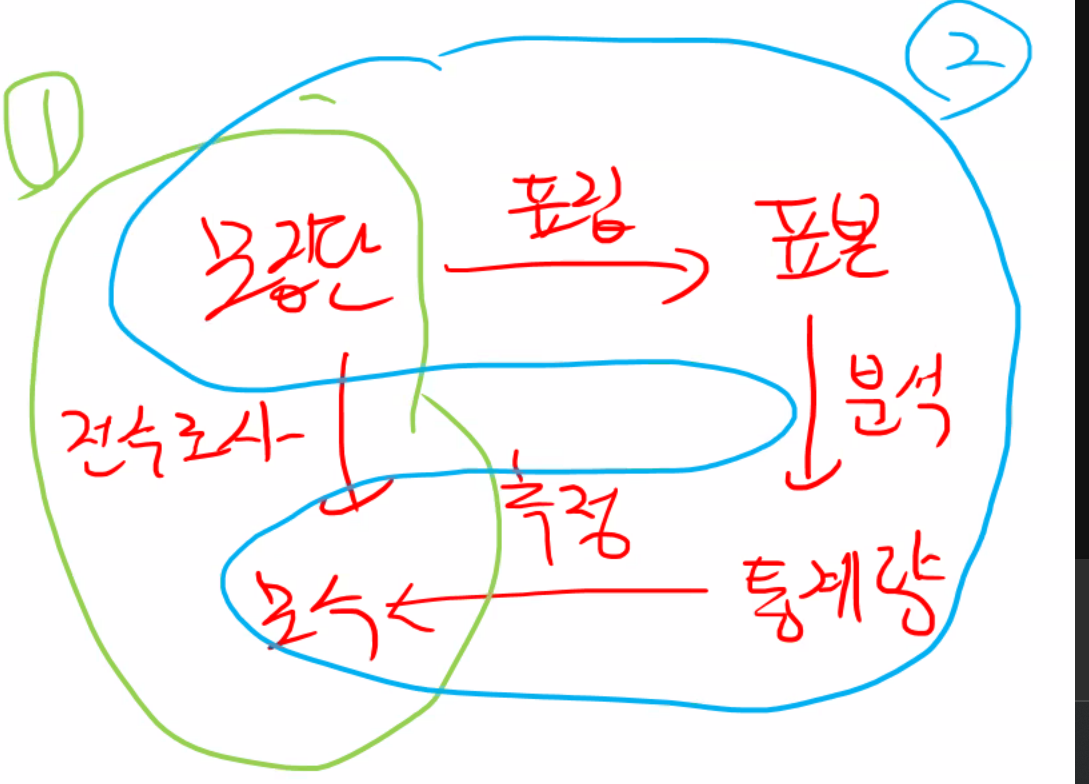
추정 estimation

통계량으로부터 모수를 추측하는 절차
점 추정(point estimate): 하나의 수치로 추정
구간 추정(interval estimate): 구간으로 추정

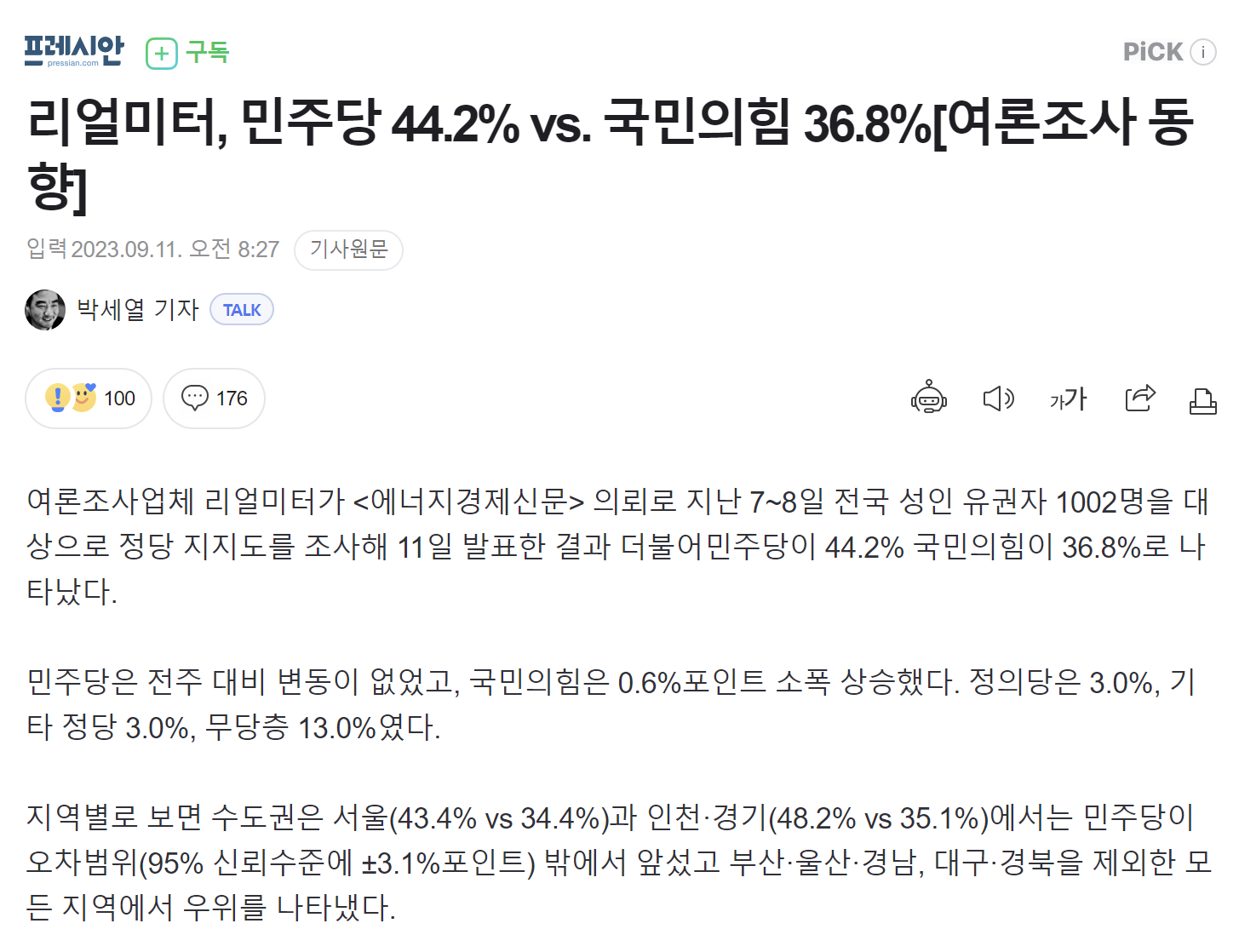
출처https://n.news.naver.com/mnews/article/002/0002300017?sid=100
ex) 뉴스 기사
'지지율이 43.4% 정도 나왔습니다.'(점 추정 같으나)
±3.1%
40.3% ~ 46.5%(실제로는 구간 추정)
사람들은 애매하게 얘기하면 싫어하기때문에 입맛에 맞춰주는 거임

신뢰 구간(confidence interval)

대표적인 구간 추정 방법
신뢰구간 = 통계량±오차범위
신뢰해도 된다는 뜻은 아니고 만든 사람이 그렇게 이름을 지어놓은 것
모집단에서 표본을 추출하면, 약간의 차이가 발생할 수 있음 (=표집오차)
오차 범위(=표집 오차가 발생할 범위)를 추정
통계량이 모수의 일정 오차 범위 내에서 관찰 → 역으로 관찰된 통계량에서 해당 오차 범위 내에 모수가 있을 것으로 추정

신뢰수준(confidence level)

이론적으로 나올 수 있는 최대의 오차는 매우 큼
실제로는 모수와 가까운 일부에서 대부분의 결과가 나옴
무한히 다양한 가능성을 모두 고려할 경우 현실적으로 의사결정이 불가능하므로 흔히 나오는 범위로 제한
신뢰수준: 모수가 추정된 신뢰구간에 포함되는 표본의 비율

ex) 여론조사 100번을 하면 몇 번 정도 신뢰구간 안에 진짜 지지율이 들어가느냐
95% 신뢰수준 = 여론조사를 100번하면 신뢰구간 안에 진짜 지지율이 95번은 들어간다 (5번은 안 들어간다)
40.3% ~ 46.5%
100% 신뢰수준 0% ~ 100% => 아무 의미가 없음(하나마나한 이야기) 쓰지 않는다

신뢰 수준과 신뢰 구간의 관계

높은 신뢰수준 → 많은 표본을 포함 → 넓은 오차범위 → 적은 정보
낮은 신뢰수준 → 적은 표본을 포함 → 좁은 오차범위 → 많은 정보
*오차범위(여유를 주는것)
"적은 정보"의 의미: 신뢰수준이 높다는 것은 다양한 가능성을 고려한다는 의미이므로, 의사결정을 내리기가 어려워짐
신뢰수준은 적절한 수준에서 타협이 필요
의사결정에 필요할 만큼의 정보를 담고 있으면서
충분히 많은 표본을 포함해야 함
교과서적으로는 95%, 99% 등을 추천하나 절대적 기준은 없음

신뢰수준 != 믿을 수 있는 수준

± Window 기준(ㄷ + 한자 -> 6)

※ 데이터를 왜 많이 모아야하는가?

같은 신뢰수준에서라도 데이터가 많으면 오차범위가 작다

반대로 말하면 얼마나 데이터를 많이 모아야하나?

-> 의사결정에 필요한만큼만 모으면 된다..

T라는 값이 처음 나온 논문을 보면
예로 드는 데이터 개수가 4건
이론적으로는 데이터 개수가 2건만 있어도 통계적으로 올바른 추정은 됨

의사결정할 기준이 불분명 -> 많으면 많을 수록 좋다...(그러나 데이터가 많다는 것은 대체로 돈이 많이 들던지 시간이 든다는 이야기)

부트스트래핑(bootstrapping)

평균과 달리 중간값 최빈값 등의 통계량은 표집분포의 형태를 간단히 알기 어려움
표본이 충분히 크면 부트스트래핑이라는 시뮬레이션 기법을 사용해서 신뢰구간을 추정
import

여론조사의 "표본오차" 항목

오차범위 수준 ±3.1% 틀렸음(저건 전체 1000명일때고...)
대충 서울에서 인원수 200명 정도 조사했을텐데 오차범위는 7% 정도, 인천.경기 따로 표시해줘야 맞는거임

1.96 * 50 / np.sqrt(n)이디어에 지지율이 30%는

(1) 내 사업 아이디어에 지지율이 30%는
나와야 사업을 해볼만하겠다
(2) 10명한테 물어보니까 4명이 지지
(3) 지지율 40% ± 오차범위 30%
= 10% ~ 70%
(4) 몇 명은 더 조사를 해봐야할까?
-> 오차범위를 얼마나 좁혀야하나?
(5) 나는 오차범위가 ±10%까지는 줄어야
결론이 난다
(6) n = 100일 때 오차범위 ±9.8%니까
그 정되면 되겠군

실제로 대통령 선거는
1% 안쪽에서 승패가 결정
9000명은 조사해야함..
여론조사 회사도 영세, 언론사도 경영이 어려움

그냥 1000명 조사하자..(돈과 시간이 없기때문에)
500명은 너무 작아보이고ㅋㅋ