
코딩테스트 문제를 풀다가 문득 .count의 시간복잡도에 대한 의문이 생겨서 파헤쳐봤습니다.
입력값을 거르는 과정에서 .count를 이용해 걸러줄 것인가?
거르지 않아도 함수 내부 로직에서 O(n)의 시간복잡도로 걸러지는 구조이다.
즉, 다른 말로 하자면?.count가 O(n)의 시간복잡도를 가진다면 손해, O(1)라면 이득인 구조.
그래서 찾아보니, collection이 RandomAccessCollection 프로토콜에 부합하면,
instance property인 count가 O(1)의 시간복잡도를 가진다고 하네요?
부합 안 하면 O(n) 이래요.
제가 뭐 어떻게 지어낸 말이 아니라 애플이 그렇대요.
Complexity
O(1) if the collection conforms to RandomAccessCollection; otherwise, O(n), where n is the length of the collection.
Source: Apple Developer Documentation
그래서...
RandomAccessColletion
은 또 뭔지 찾아봤습니다.
오호... 흥미롭네요...
이 프로토콜에 대해선 나중에 따로 글을 써 보도록 하고,
일단은 요점만 쓰자면, Array의 경우 Array의 Element가 Copyable과 Escapable 프로토콜을 따르는 경우, RandomAccessColletion 프로토콜에 부합한다고 하네요.
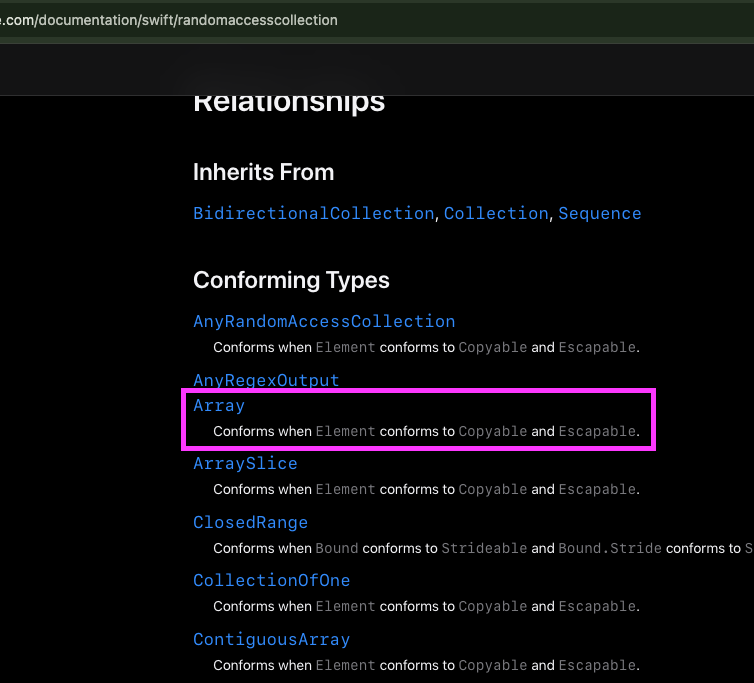
일단 Character는 Copyable 프로토콜을 따릅니다.
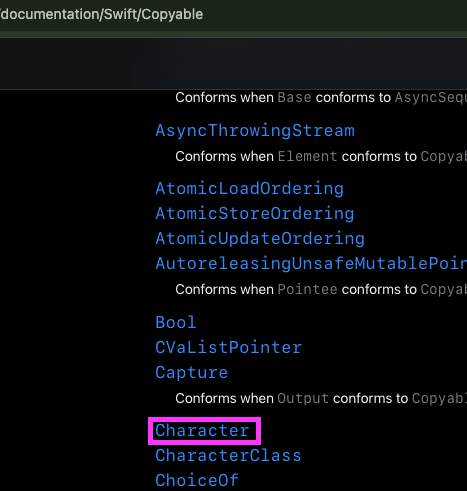
그럼 Escapable은?
공식문서에서 찾아봐도 안 나오네요?
Swift 6에서 새롭게 도입된 프로토콜인 것 같은데... 일해라 애플
일단은 여기선 String과 Character가 Escapable 프로토콜을 준수한다고 하니,
참이라고 간주하고 이어가자면,
지금처럼 [Character]를 쓰는 케이스에선 RandomAccessCollection 프로토콜에 부합하는 Collection이니, O(1)의 시간복잡도로 count를 활용할 수 있을 것으로 추론했습니만...!
뻘짓이었습니다
그 문제가요...
사실 입력으로 String을 받는 경우였고...
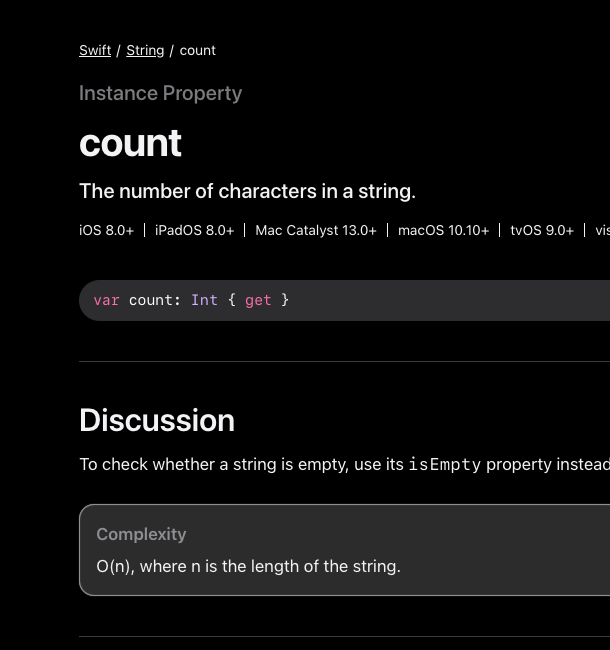
String의 인스턴스 프로퍼티 count는 O(n)의 시간복잡도를 가진다고 공식문서에 명시되어 있네요.

그래도 지식이 늘었잖습니까?
한 잔 합시다.

그래도 오늘까지 배운 지식으로 추론해보면,
나중에 공식문서에서 String의 .count가 O(1)의 시간복잡도로 변경될 수도 있지 않을까? 하는 추측을 남겨놓습니다.
하지만 추론 과정 중, Array == Collection이지만 Collection != Array 이기에, 왠지 틀린 추측일 것 같아
수정합니다, 대신 위에 추측했던 것에 대한 논리 흐름을 남겨놓습니다:
- RandomAccessCollection 프로토콜에 부합하는 Array의 count는 O(1)의 시간복잡도를 가진다.
- Copyalbe과 Escapable 프로토콜에 부합하는 element로 이루어진 Array는 RandomAccessCollection이다.
- String은 Collection 프로토콜을 따르며, String.element는 Character이다.
- Character는 Copyable과 Escapable 프로토콜을 준수한다.
따라서, [Character]의 .count는 O(1)의 시간복잡도를 가질 것이다.
졸려서 내일 확인해봐야겠네요.
