[PS] 그래프

1) 그래프

그래프란?
: 점과 선으로 관계를 나타낸 것

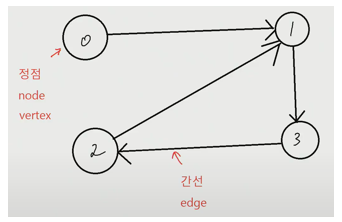
인접행렬(2차원 배열)

arr[form][to]로 표현가능 하며, arr[A][B] = 1 의 의미는 A -> B로 가는 간선이 있다는 의미이고, arr[A][B] = 0는 A -> B로 가는 간선이 없다는 것을 의미한다.
인접행렬의 특징

• 모든 관계가 표현된다.
• 메모리 공간 낭비가 심하다. (메모리 수 = node개수의 제곱)

메모리 공간 낭비를 해결하기 위해서는 인접 리스트 방식을 사용할 수 있다.

인접 행렬		그래프
	=>

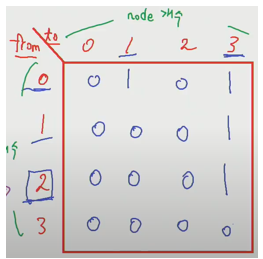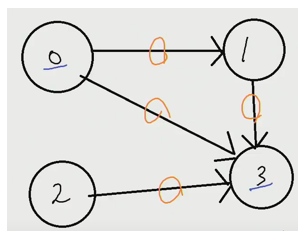인접행렬 코드

	int arr[5][5] = { 0 };
	int nodeCnt, edgeCnt;
    // 첫줄에는 node 갯수와 edge 갯수 입력
	cin >> nodeCnt >> edgeCnt;
    // 다음줄 부터는 간선 정보 입력
	for (int i = 0; i < edgeCnt; i++) {
		int from, to;
		cin >> from >> to;
		// 입력된 행렬에 간선 넣기
		arr[from][to] = 1;
	}
	// 3에서 어디로 가는 간선이 있는지 찾기 위해
	int from = 3;
	for (int to = 0; to < nodeCnt; to++) {
		if (arr[from][to] == 0) continue;
		cout << to << " ";
	}
	// 3에서 4로 가는 간선이 있기 때문에 출력은 4

입력	인접 행렬	출력

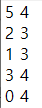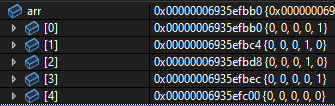인접리스트

인접리스트는 vector<vector<int>>로 표현할 수 있다.

인접리스트의 특징

• 메모리가 작다. (메모리 수 = edge 갯수)
• 특정 간선을 찾을 때 효율이 좋지 않다.

인접 리스트		그래프
	=>

인접리스트 코드

vector<int> v[5];

	int nodeCnt, edgeCnt;
	// 첫줄에는 node 갯수와 edge 갯수 입력
	cin >> nodeCnt >> edgeCnt;
	// 다음줄 부터는 간선 정보 입력
	for (int i = 0; i < edgeCnt; i++) {
		int from, to;
		cin >> from >> to;
		// 입력된 리스트에 간선 넣기
		v[from].push_back(to);
	}
	// 3에서 어디로 가는 간선이 있는지 찾기 위해
	int from = 3;
	for (int i = 0; i < v[from].size(); i++) {
		int to = v[from][i];
		cout << to << " ";
	}
	// 3에서 4로 가는 간선이 있기 때문에 출력은 4

입력	인접 리스트	출력
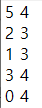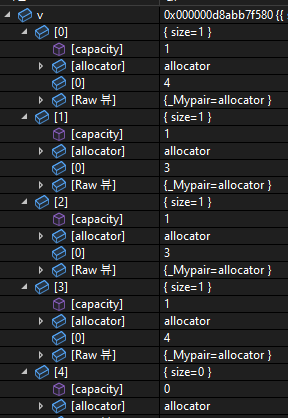