[PS] DFS(Depth First Searching)

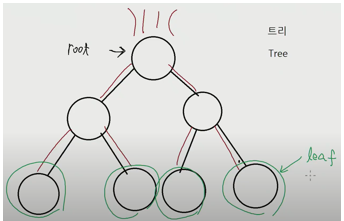
1) 트리

트리의 특징

• 노드 개수 : n개 이면 간선 개수 : n-1개가 된다.
• Cycle를 이루지 않는다.
• 두 Node간의 경로가 유일하게 나온다.

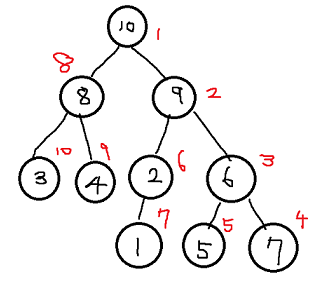
Binary Tree(2진 트리)

2진트리의 특징

• 트리의 왼쪽 자손은 현재 node의 2배랑 같다.
• 트리의 오른쪽 자손은 현재 node의 2배 + 1과 같다.

2) DFS

인접 행렬 방식

#include <iostream>
using namespace std;

int arr[100][100] = { 0 };
int nodeCnt;
int used[100];

void func(int now) {

	cout << now << " ";

	// 한 Node에서 갈 수 있는 node가 2개 이상일 경우 작은 번호의 node 부터
	for (int to = 1; to <= nodeCnt; to++) {
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
        if(used[to] != 0) continue;
        // now -> to로 갈 수 없으면 무시
		if (arr[now][to] == 0) continue;
        used[to] = 1; // 도착한 node 기록
		func(to);
	}
}

int main() {
	
	// Node 개수
	cin >> nodeCnt;
	// Node 개수만큼의 Node 정보
	// 트리의 간선 수 : 노드 - 1
	for (int i = 0; i < nodeCnt - 1; i++) {
		int from, to;
		cin >> from >> to;
		// 인접행렬 방식
		arr[from][to] = 1;
	}
	
    used[10] = 1;
	// root를 10으로 설정
	func(10);

	return 0;
}

입력	그래프	출력(경로)

인접 리스트 방식

#include <iostream>
#include <vector>
using namespace std;

vector<int> v[100];
int nodeCnt;
int used[100];

void func(int now) {

	cout << now << " ";

	// 한 Node에서 갈 수 있는 node가 2개 이상일 경우 먼저 입력받은 node 부터
	for (int i = 0; i < v[now].size(); i++) {
		int to = v[now][i];
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
		if (used[to] != 0) continue;
		used[i] = 1; // 도착한 node 기록
		func(to);
	}
}

int main() {
	
	// Node 개수
	cin >> nodeCnt;
	// Node 개수만큼의 Node 정보
	// 트리의 간선 수 : 노드 - 1
	for (int i = 0; i < nodeCnt - 1; i++) {
		int from, to;
		cin >> from >> to;
		// 인접리스트 방식
		v[from].push_back(to);
	}

	used[10] = 1;
	// root를 10으로 설정
	func(10);

	return 0;
}

입력	그래프	출력(경로)

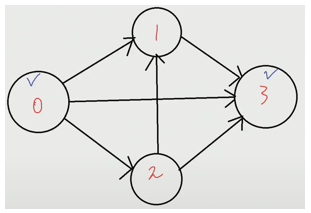
3) 특정 목적지까지 가는 방법의 수

인접 행렬 방식

0번에서 출발하여 3번까지 가는 경로의 개수 구하기

#include <iostream>
using namespace std;

int arr[100][100] = { 0 };
int nodeCnt,edgeCnt;
int used[100];
int cnt;

void func(int now) {

	// 3에 도착하게 되면 카운트
	if (now == 3) {
		cnt++;
		return;
	}

	for (int to = 0; to <= nodeCnt; to++) {
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
		if (used[to] != 0) continue;
		// now -> to로 갈 수 없으면 무시
		if (arr[now][to] == 0) continue;
		used[to] = 1; // 도착한 node 기록
		func(to);
		used[to] = 0; // 다양한 경로로 이동이 가능토록 하기 위해
	}
}

int main() {

	// Node 개수 와 간선 개수
	cin >> nodeCnt >> edgeCnt;
	// 간선 개수만큼의 Node 정보
	for (int i = 0; i < edgeCnt; i++) {
		int from, to;
		cin >> from >> to;
		// 인접행렬 방식
		arr[from][to] = 1;
	}

	used[0] = 1;
	// root를 0으로 설정
	func(0);
	// 경로 개수
	cout << cnt;

	return 0;
}

인접 리스트 방식

#include <iostream>
#include <vector>
using namespace std;

vector<int> v[100];
int nodeCnt,edgeCnt;
int used[100];
int cnt;

void func(int now) {

	// 3에 도착하게 되면 카운트
	if (now == 3) {
		cnt++;
		return;
	}

	for (int i = 0; i < v[now].size(); i++) {
		int to = v[now][i];
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
		if (used[to] != 0) continue;

		used[to] = 1; // 도착한 node 기록
		func(to);
		used[to] = 0; // 다양한 경로로 이동이 가능토록 하기 위해
	}
}

int main() {

	// Node 개수 와 간선 개수
	cin >> nodeCnt >> edgeCnt;
	// 간선 개수만큼의 Node 정보
	for (int i = 0; i < edgeCnt; i++) {
		int from, to;
		cin >> from >> to;
		// 인접리스트 방식
		v[from].push_back(to);
	}

	used[0] = 1;
	// root를 0으로 설정
	func(0);
	// 경로 개수
	cout << cnt;

	return 0;
}

입력	그래프	출력(경로)
		4

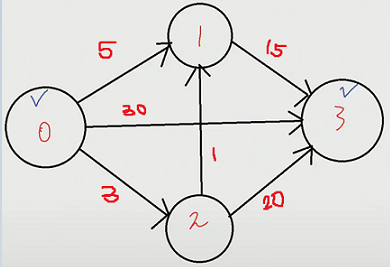
3) 최대 거리 / 최소 거리

0번에서 출발하여 3번까지 가는 최대 / 최소 거리 구하기

인접 행렬 방식

#include <iostream>
using namespace std;

int arr[100][100] = { 0 };
int nodeCnt, edgeCnt;
int used[100];
int sum;
int minCost = 21e8;
int maxCost = -21e8;

void func(int now) {

	// 3에 도착하게 되면 최대,최소 거리 구하기
	if (now == 3) {
		if (minCost > sum) minCost = sum;
		if (maxCost < sum) maxCost = sum;
		return;
	}

	for (int to = 0; to < nodeCnt; to++) {
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
		if (used[to] != 0) continue;
		// now -> to로 갈 수 없으면 무시
		if (arr[now][to] == 0) continue;
		used[to] = 1; // 도착한 node 기록
		sum += arr[now][to];
		func(to);
		used[to] = 0; // 다양한 경로로 이동이 가능토록 하기 위해
		sum -= arr[now][to];
	}
}

int main() {

	// Node 개수 와 간선 개수
	cin >> nodeCnt >> edgeCnt;
	// 간선 개수만큼의 Node 정보
	for (int i = 0; i < edgeCnt; i++) {
		int from, to, cost;
		// 출발 , 목적지 , 거리
		cin >> from >> to >> cost;
		// 인접행렬 방식
		arr[from][to] = cost;
	}

	used[0] = 1;
	// root를 0으로 설정
	func(0);
	// 최소 최대 거리
	cout << minCost << " " << maxCost << endl;

	return 0;
}

인접 리스트 방식

#include <iostream>
#include <vector>
using namespace std;

// 구조체 생성
struct Edge {
	// 목적지 , 거리
	int to;
	int cost;
};
vector<Edge> v[100];
int nodeCnt,edgeCnt;
int used[100];
int sum;
int minCost = 21e8;
int maxCost = -21e8;

void func(int now) {

	// 3에 도착하게 되면 최대,최소 거리 구하기
	if (now == 3) {
		if (minCost > sum) minCost = sum;
		if (maxCost < sum) maxCost = sum;
		return;
	}

	for (int i = 0; i < v[now].size(); i++) {
		Edge edge = v[now][i];
		int to = edge.to;
		int cost = edge.cost;
		// 이미 node에 왔었다면 무시 -> 중복(Cycle) 피하기
		if (used[to] != 0) continue;

		used[to] = 1; // 도착한 node 기록
		sum += cost;
		func(to);
		used[to] = 0; // 다양한 경로로 이동이 가능토록 하기 위해
		sum -= cost;
	}
}

int main() {

	// Node 개수 와 간선 개수
	cin >> nodeCnt >> edgeCnt;
	// 간선 개수만큼의 Node 정보
	for (int i = 0; i < edgeCnt; i++) {
		int from, to, cost;
		cin >> from >> to >> cost;
		// 인접리스트 방식
		v[from].push_back({to,cost}); // 목적지, 거리 입력
	}

	used[0] = 1;
	// root를 0으로 설정
	func(0);
	// 최소 최대 거리
	cout << minCost << " " << maxCost << endl;

	return 0;
}

입력	그래프	출력(경로)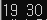