Solving Questions With Brainpower

문제설명

You are given a 0-indexed 2D integer array questions where questions[i] = [pointsi, brainpoweri].

The array describes the questions of an exam, where you have to process the questions in order (i.e., starting from question 0) and make a decision whether to solve or skip each question. Solving question i will earn you pointsi points but you will be unable to solve each of the next brainpoweri questions. If you skip question i, you get to make the decision on the next question.

• For example, given questions = [[3, 2], [4, 3], [4, 4], [2, 5]]:
  • If question 0 is solved, you will earn 3 points but you will be unable to solve questions 1 and 2.
  • If instead, question 0 is skipped and question 1 is solved, you will earn 4points but you will be unable to solve questions 2 and 3.

Return the maximum points you can earn for the exam.

제한사항

• 1 <= questions.length <= 105
• questions[i].length == 2
• 1 <= pointsi, brainpoweri <= 105

입출력 예

Example 1:

Input: questions = [[3,2],[4,3],[4,4],[2,5]]
Output: 5
Explanation: The maximum points can be earned by solving questions 0 and 3.
- Solve question 0: Earn 3 points, will be unable to solve the next 2 questions
- Unable to solve questions 1 and 2
- Solve question 3: Earn 2 points
Total points earned: 3 + 2 = 5. There is no other way to earn 5 or more points.

Example 2:

Input: questions = [[1,1],[2,2],[3,3],[4,4],[5,5]]
Output: 7
Explanation: The maximum points can be earned by solving questions 1 and 4.
- Skip question 0
- Solve question 1: Earn 2 points, will be unable to solve the next 2 questions
- Unable to solve questions 2 and 3
- Solve question 4: Earn 5 points
Total points earned: 2 + 5 = 7. There is no other way to earn 7 or more points.

행동영역(알고리즘을 설계하는 사고과정)

1. 규칙 파악하기

• 2차원 배열에서 요소 하나를 선택하여 문제를 풀었을때, 그 배열의 첫번째 요소만큼 건너뛰어야 다음 문제를 풀 수 있다.
• 문제를 한개 건너뛴다면 다음 문제로 넘어간다.
  
  

2. 알고리즘 설계하기

• 반복문으로 순회하며 총합을 저장하는 배열을 만든 후, 그 배열에서 가장 큰 값을 찾는 식으로 생각했다.

답

/**
 * @param {number[][]} questions
 * @return {number}
 */

// Recursion
var mostPoints = function(questions) {
    const n = questions.length;

    function dp(i) {
        if (i >= n) return 0;

        let take = questions[i][0] + dp(i + questions[i][1] + 1);
        let notTake = dp(i + 1);
        return Math.max(take, notTake);
    }
    return dp(0);
};
// TC: Exponential
// SC: O(n)

속도 백분위

Runtime: 156 ms
Memory Usage: 81.6 MB

피드백

재귀 알고리즘과 동적 프로그래밍에 대한 지식이 있어야 풀 수 있는 문제였다.

동적 프로그래밍

동적 프로그래밍이란, 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 현재 상태가 어디서 오는지 관찰해야한다.
주로 최소, 최대, 경우의 수 문제는 DP 문제일 확률이 높다.

예시

[피보나치 수열]

① DP식 정의 : d[i] = i번째 피보나치 수
② DP식 세우기 : d[i] = d[i-1] + d[i-2]
③ DP식 초기화 : d[0] = d[1] = 1

중복의 문제를 해결하기 위해서는 중복된 값을 여러번 계산하지 않도록 값을 기억해둘 수 있는데, 이를 Memoization 이라고 한다.
d라는 배열에 index값은 n번째 피보나치수와 같기 때문에 d 배열에서 n번째 피보나치수를 요청할 때 꺼내오기만하면 된다.

function f(n) {
    let d = Array(n + 1).fill(0); // 👈 Memoization
    d[0] = 0;
    d[1] = 1;
    for (let i = 2; i <= n; i++) {
        d[i] = d[i - 1] + d[i - 2];
    }
    return d[n];
}
console.log(f(4)); // 3

재귀 알고리즘

재귀함수란, 자기 자신을 다시 호출하는 함수를 말한다.

위의 코드에서 factorial(n)은 n * factorial(n - 1);을 반환한다.
이때, factorial(n - 1)을 계산하기 위해 factorial(n - 1)를 호출한다. 그러면 factorial(n - 1)의 결과 값으로 (n - 1)factorial(n - 2)이 나오며, 이는 n의 값이 종료조건에 도달할때까지 함수가 반복된다.

이는 함수가 자기 자신을 호출하면 이 호출은 호출한 함수의 실행을 일시 중단하고 새로운 함수 호출을 처리하는 원리를 가지고 있기 때문이다.

특징

재귀함수는 스택처럼 호출한 함수를 쌓았다가 종료조건을 만나면 위에서부터 하나씩 꺼래 처리하는 방식이다.

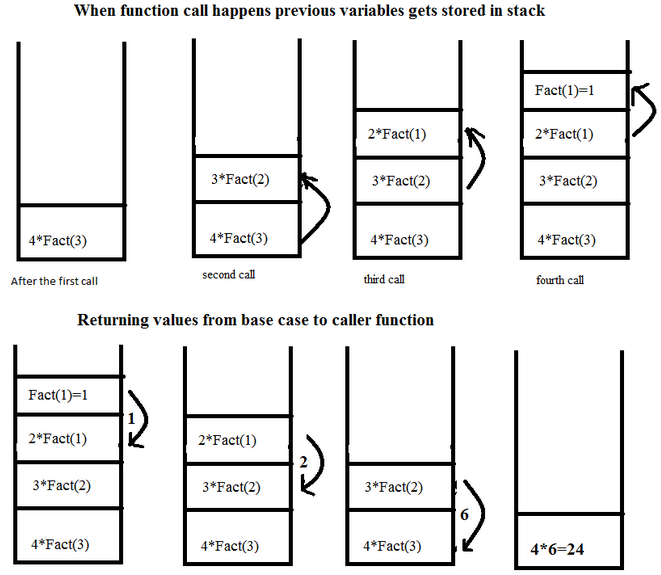
• 재귀 호출은 점화식과 종료조건만 구현하면 만들 수 있기 때문에 가시성이 높고, 구현하기 쉽다는 장점이 있다.

• 단, 1000번(약 997번) 정도까지만 재귀호출이 가능하기 때문에 많은 호출이 필요할 때에는 사용이 불가하다.

• 재귀호출과 반복문 구현은 시간 복잡도는 같으나, 실제 Call Stack에 과정에서 재귀호출이 속도가 느리고, 메모리를 크게 차지한다.
  즉, 반복문 구현은 전체 과정을 서술해야하기 때문에 재귀호출 보다 구현이 복잡하나 속도가 빠르고 호출의 제한이 없다는 장점이 있다.

---

좀 더 깊이 공부해보면, 함수가 호출될때 그 함수의 실행 컨텍스트가 생성된다. 이 컨텍스트에는 함수의 매개변수, 지역 변수 등 함수 실행에 필요한 정보가 포함된다. 그런 다음 함수의 본문이 실행되며, 만약 함수 본문에서 다른 함수를 호출하면 현재 실행 중인 함수의 실행은 일시 중단되고 새로운 함수의 실행 컨텍스트가 생성되어 그 함수가 실행된다.

• 실행 컨텍스트란, 실행할 코드에 제공할 환경 정보들을 모아놓은 객체를 말한다. 모든 JavaScript 코드는 실행 컨텍스트 내부에서 실행되기 때문에 실행 컨텍스트는 자바스크립트 코드가 실행되는 환경이라고 할 수 있다.

자세한건 여기를 참고하자.

https://velog.io/@jewon119/01.알고리즘-기초-재귀-호출Recursive-Call
https://velog.io/@edie_ko/js-execution-context

재귀적 동적 프로그래밍을 이용한 문제분석

이 문제를 처음 봤을때, 동적프로그래밍에 대한 개념이 제대로 잡혀있다면 규칙을 통해 문제의 최적 해결책이 부분 문제의 최적 해결책으로부터 도출될 수 있다는 것을 파악하여, 재귀적 동적 프로그래밍으로 문제를 풀 수 있을 것 같다는 생각이 떠오를 수 있어야한다.

왜냐하면 이 문제의 경우, 하나의 문제를 풀거나 건너뛸 때 그 결정이 다른 문제를 푸는 데에 영향을 미치지 않기 때문에 각 문제를 독립적으로 생각하고 접근할 수 있다. 또한 문제를 풀거나 건너뛰는 선택은 문제의 순서에 따라 달라지므로, 각 문제를 리스트의 인덱스를 기준으로 하여 하위 문제로 정의할 수 있다.
(최적 부분 구조를 파악하고 문제를 작은 하위 문제로 분해한다는 것을 볼 수 있다. 이 뜻은 곧 작은 부분 문제에서 구한 최적의 답을 구한다면, 큰 문제의 최적의 답을 구할 수 있다는 뜻과 같다)

이렇게 되기 위해서는 먼저 동적 프로그래밍을 작성하기 위한 원칙이 무엇인지 개념부터 잡혀 있어야한다. 만약에 잡혀있다면, 파악한 규칙을 동적프로그래밍을 통해 단계적으로 작성하며 문제를 해결할 수 있다.

지금 이 문제의 경우, 규칙을 본다면 "questions" 리스트의 각 항목은 특정 문제를 나타낸다. 그리고 그 문제란, 문제를 풀었을때 얻는 점수와 그 문제를 풀기 위해 건너뛰어야 하는 문제의 수가 주어지는 것을 말하며, 이는 questions의 요소라고 할 수 있다. 예를 들어 questions[0]에서 문제를 풀건지 풀지 않을건지 선택이 두가지로 나뉜다. 만약 문제를 푼다면 questions[0][1]만큼 건너뛰어야한다. 그리고 questions[0][1]만큼 건너 뛰었다면, 다음에 풀 문제는 questions[questions[0][1]+1]가 될 것이고, questions[questions[0][1]+1]에서도 questions[0]과 마찬가지로 문제를 풀건지 말건지를 정하는 문제가 될 것이다. 따라서 questions[0]의 문제는 questions[0]에서 구할 수 있는 값의 경우의 수에서 가장 큰 값을 고르는 문제라고 볼 수 있다. 이 작업을 questions[0]부터 questions[n-1]까지 재귀함수를 이용하여 수행한다.

후기

분명 최대 공약수 알고리즘 문제를 풀때 재귀함수에 대한 공부를 했지만 문제를 풀때 떠오르지 않았다. 기초를 좀 더 다져야겠다.