[Algorithm] 10844. 쉬운 계단 수

10844: 쉬운 계단 수(DP)

https://www.acmicpc.net/problem/10844

• 문제 티어 : S1
• 풀이 여부 : Solved
• 소요 시간 : 41:27

정답 코드

import sys
input = sys.stdin.readline

N = int(input())
dp = [[0 for _ in range(10)] for _ in range(N+1)] # N의 최댓값 100
for i in range(1, 10):
  dp[1][i] = 1 # N=1 -> [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]

for i in range(2, N+1):
  for j in range(10):
    if j == 0:
      dp[i][j] = dp[i-1][1]
    elif j == 9:
      dp[i][j] = dp[i-1][8]
    else:
      dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]

print(sum(dp[N]) % 1000000000)

접근 방식

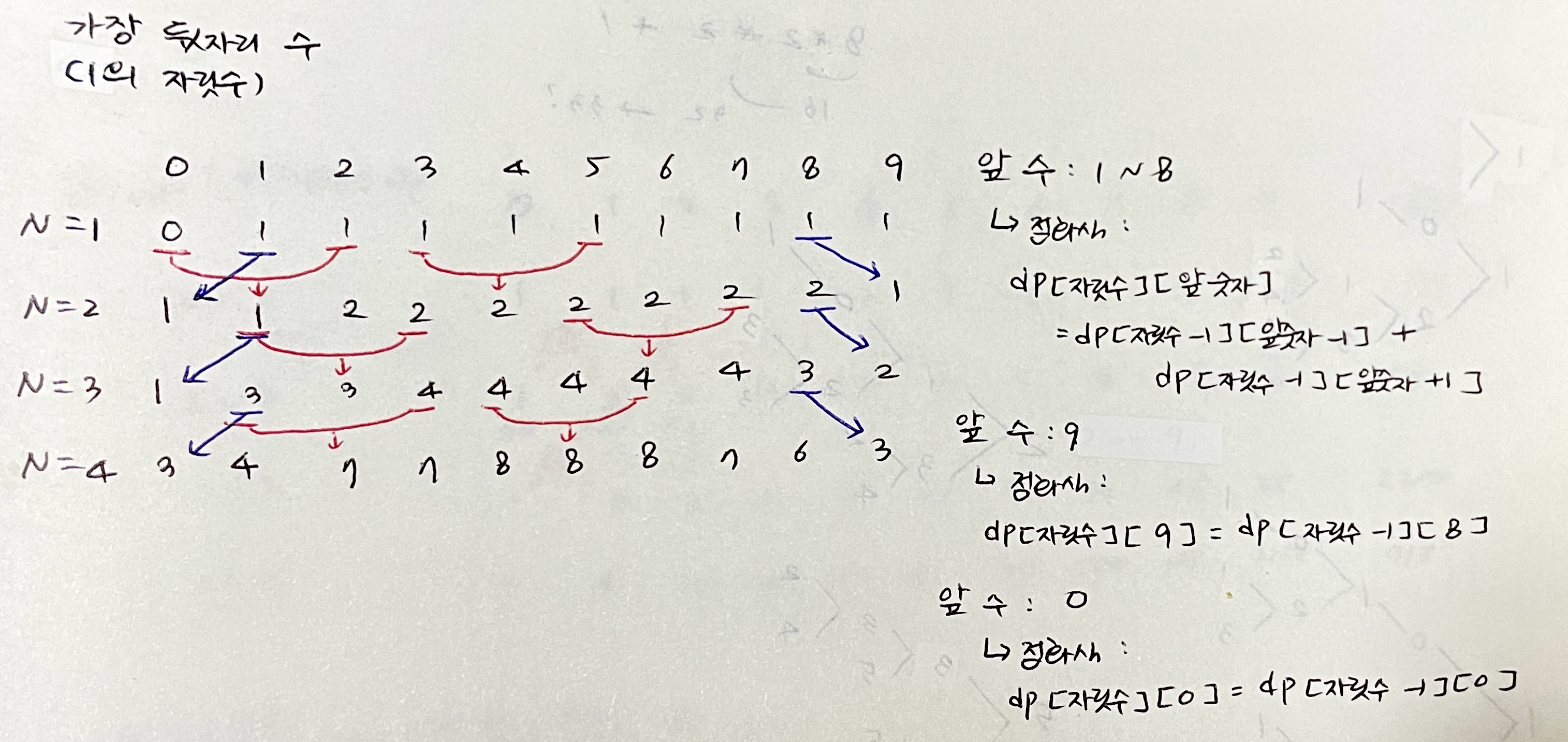
계단수를 이루기 위한 경우의 수 (뒷자리 기준)

0 : 1 → 1가지

1 : 0, 2 → 2가지

2: 1, 3 → 2가지

3: 2, 4 → 2가지

4: 3, 5 → 2가지

5: 4, 6 → 2가지

6: 5, 7 → 2가지

7: 6, 8 → 2가지

8: 7, 9 → 2가지

9: 8 → 1가지

→ 0, 9: 1가지, 1~8 : 2가지 경우의 수 존재

바텀업 방식의 DP를 사용해 가장 뒷자리수를 기준으로 가능한 경우의 수를 구하는 방식은 아래와 같이 점화식으로 표현할 수 있다.

1. 앞 수가 1~8의 경우

$dp[자릿수][앞숫자] = dp[자릿수-1][앞숫자-1] + dp[자릿수-1][앞숫자+1]$

1. 앞 수가 0인 경우

$dp[자릿수][0] = dp[자릿수-1][1]$

1. 앞 수가 9인 경우

$dp[자릿수][9] = dp[자릿수-1][8]$

배운점 또는 느낀점

점화식을 세우기 위해 N=1, N=2, N=3 정도의 경우의 수를 직접 나열해보면서 사이의 관계 파악하기