📚 BST

이번 게시글에는 BST(Binary Search Tree)에 대해서 정리 해보도록 하겠다.

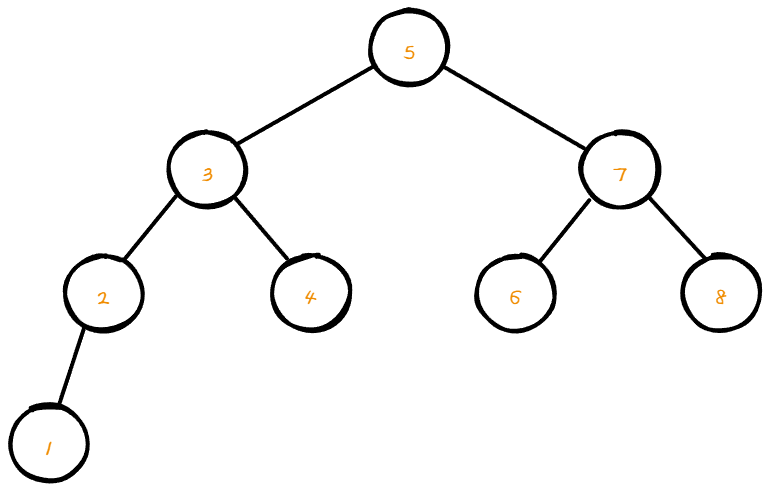
BST는 저장과 동시에 정렬이 이루어지고 자식 노드의 개수가 2 이하인 이진트리이다.
어느 노드를 선택하든 해당 노드의 왼쪽 서브트리 node들은 해당 노드의 값보다 작은 값으로 이루어져 있다.
노드의 왼쪽 서브트리 node들은 해당 노드의 값보다 큰 값들을 지닌 노드들로만 이루어져있다.
위 그림은 root node를 기준으로 하였다.

검색, 저장, 삭제의 시간복잡도는 O(logN)이며 한쪽으로 치우쳐진 불균형한 트리의 경우 O(n)의 시간 복잡도를 가질 수 있다.

📝 높이 계산

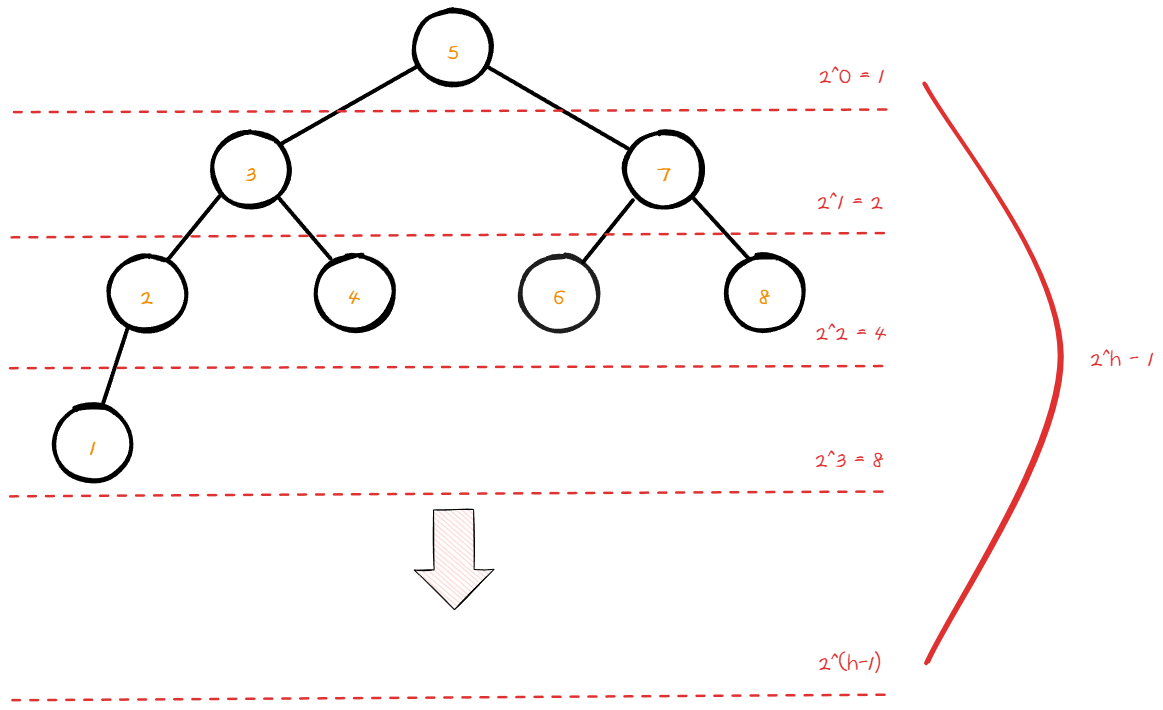
h를 높이라고 가정한다.

a * (r^h - 1) / (r - 1) 는 등비수열의 합 계산 공식이다.
여기서 a는 첫 번째 항 (2^0 = 1), r은 공비(2), h는 항의 개수이다.

S = 1 * (2^h - 1) / (2 - 1) = 2^h - 1

즉, 2^0 부터 2^(h-1) 까지의 합은 2^h - 1

총 개수 n = 2^h - 1를 변환하면 n+1 = 2^h

n+1 = 2^h => log_2(n+1) = log_2(2^h) => log_2(n+1) = hlog_2(2)

log_2(n+1) = h이다.

해당 값을 어림추산 하여 logn과 동일하다고 본다.

🔍 탐색

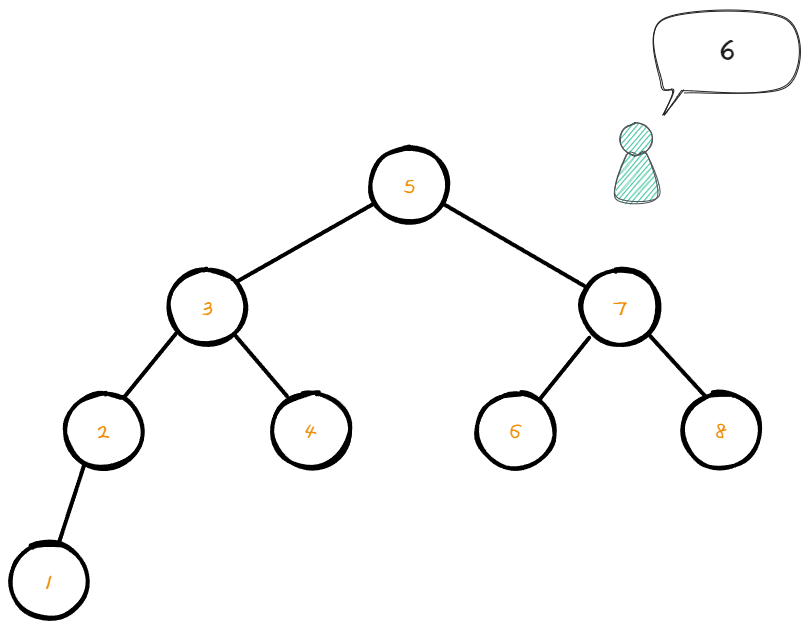
만약 6의 데이터를 가지고 있는 node를 찾고 싶다면 어떻게 탐색 해야 할지 알아보자.
먼저 현재 root node의 data값은 5이다.
이 뜻은 root node의 왼쪽 서브트리는 5의 값보다 작아야 한다는 것 이다.
탐색할 숫자는 6으로 5보다 크기 때문에 오른쪽 서브트리를 탐색 해야 할 것이다.

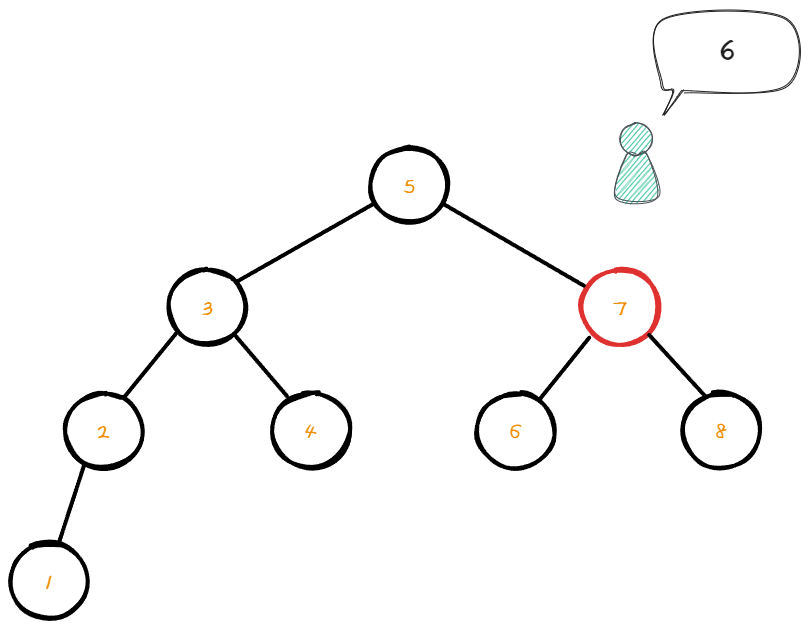
오른쪽 서브트리로 이동해서 node의 데이터 값을 확인 해 보았다.
해당 node의 데이터 값은 7이므로 현재 찾아야 할 6보다 값이 크다.
7보다 작은 값을 찾기 위해선 왼쪽의 서브트리로 이동해야한다.

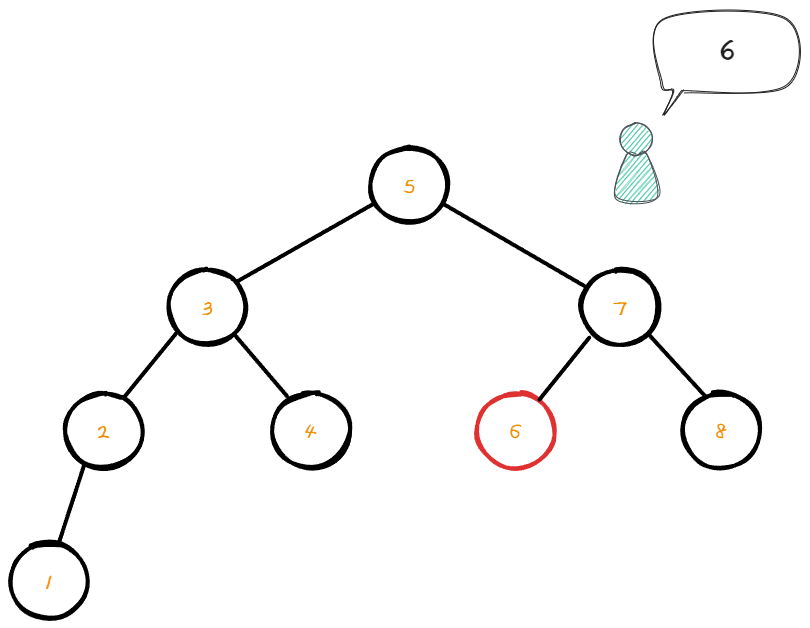
왼쪽의 서브트리로 이동한후 데이터를 확인해보니 6이 나온다.

위 그림의 트리 높이는 logn이다 따라서 시간복잡도 역시 O(logn)이다.

🤔 worst case

그렇다면 worst case역시 시간복잡도가 O(logn)일까?

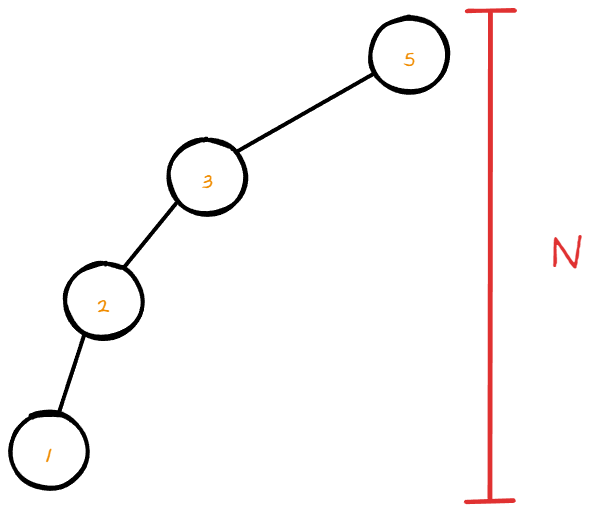
위 그림에서는 오른쪽 서브트리가 존재하지 않고 왼쪽 서브트리만 존재한다.
연결리스트와 다를 바 없는 형태이다.
트리의 높이가 n이기 때문에 worst case의 시간복잡도 역시 O(n)이다.

편향 트리를 해결 하기 위해 자가 균형 이진 탐색 트리가 존재 한다.
대표적으로 AVL트리와 Red-black 트리가 있으며 Java에서는 hashmap의 seperate chaning으로써 Linked list와 Red-black tree를 병행하여 저장 하기도 한다.

🧩 삽입

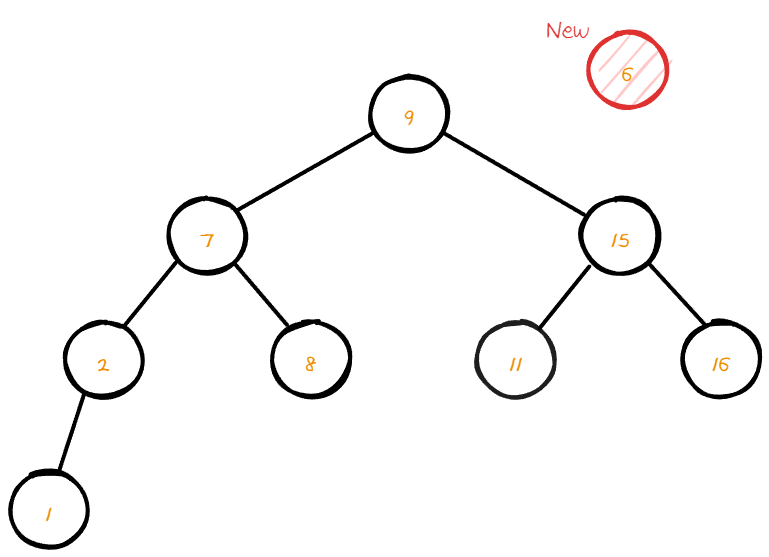
위 그림처럼 BST에 6의 데이터 값을 가지고 있는 node가 삽입 된다고 가정 해보자.
해당 node를 삽입하기 위해 root node부터 탐색을 시작 할 것이다.

탐색을 시작하며 데이터를 비교 후 자리를 찾아갈때 까지 반복한다.

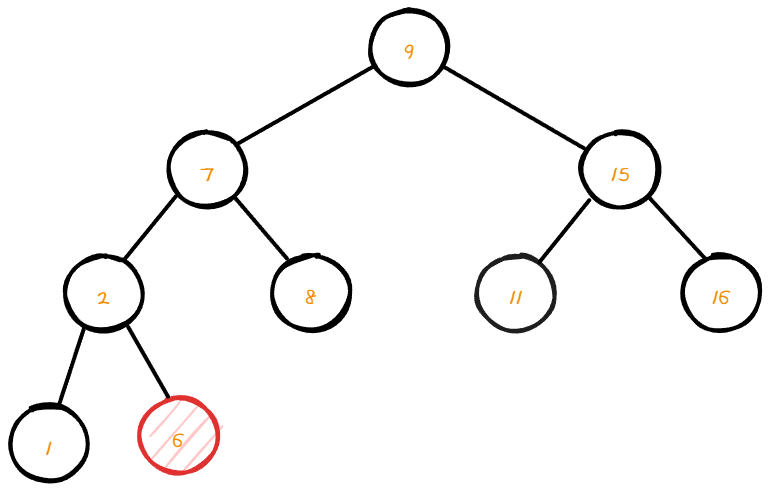
1. 데이터 9와 비교 후 좌측 노드로 이동
2. 데이터 7과 비교 후 좌측 노드로 이동
3. 데이터 2와 비교 후 우측 노드로 이동
4. 우측 노드가 존재하지 않으니 해당 자리로 삽입

📦 삭제

📌 리프 노드 삭제

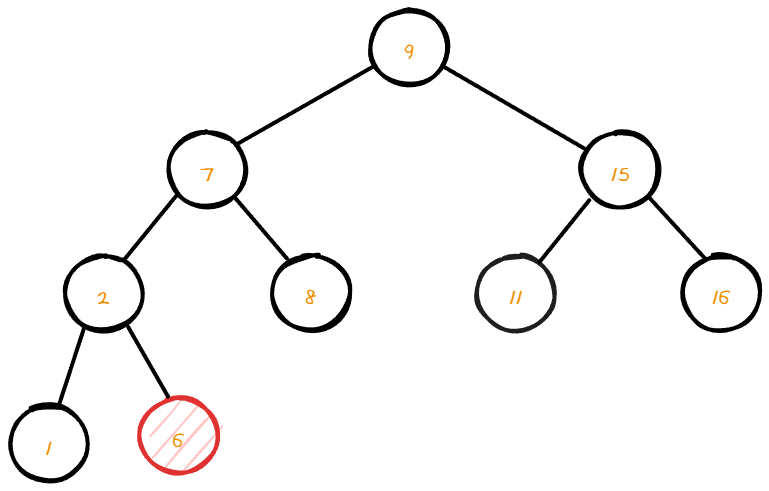
리프 노드는 트리의 끝에 삽입 되어 있는 node이며 리프 노드를 삭제 하기 위해서는 별 다른 과정 없이 해당 노드를 지워 주면 된다.

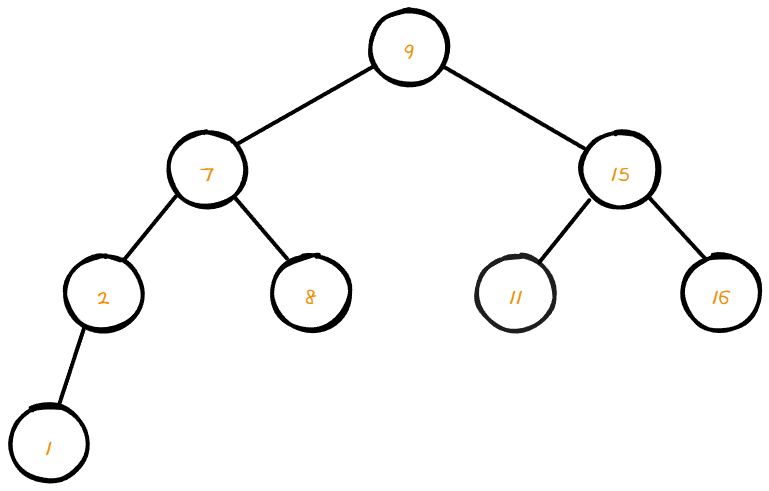
📌 자식 노드가 1개인 노드 삭제

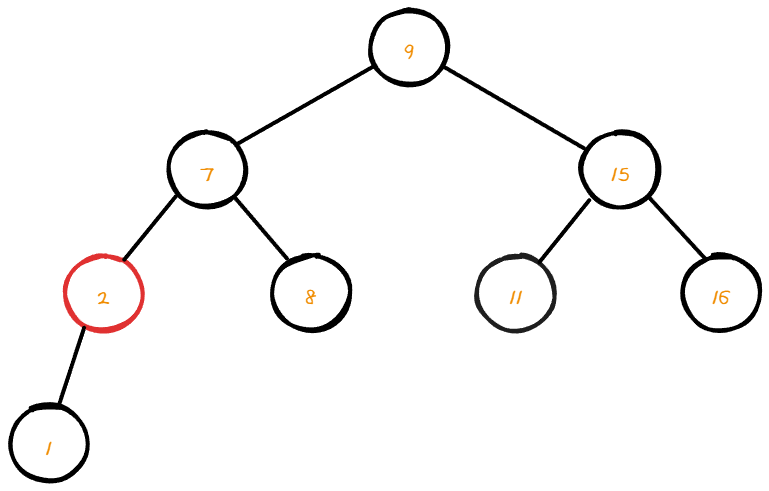
data가 2인 node를 삭제 하려 한다.
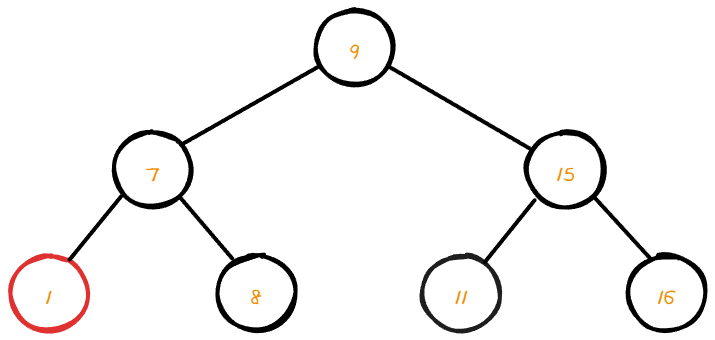
해당 node를 삭제 해준 후 자식 node와 위치를 변경 한다.

📌 자식 노드가 2개인 노드 삭제

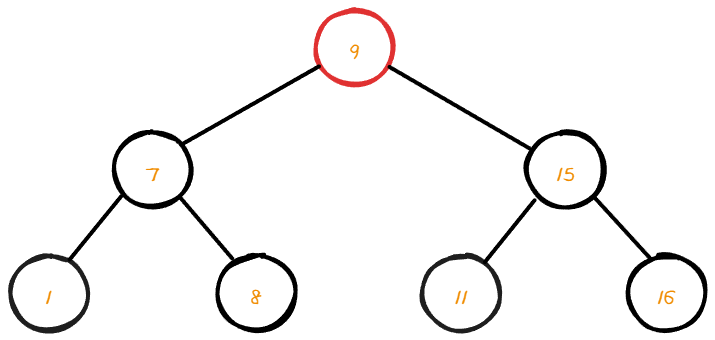
자식 node가 2개인 root node를 target 하여 삭제 하려 한다.
root node를 삭제 해주기 위해서는 우측 서브트리에서 가장 작은 최소 값을 찾아야 한다.

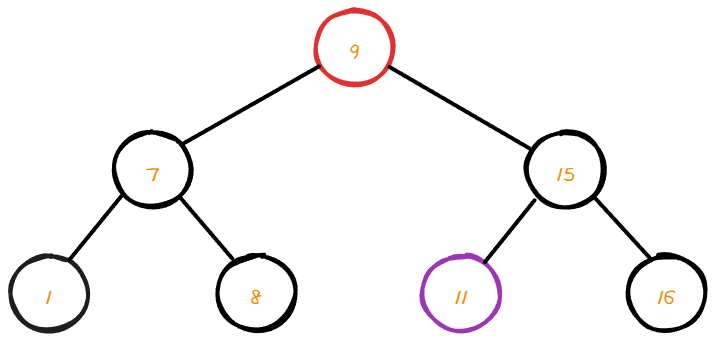
우측 서브트리에서 최소 값을 찾았다면 삭제할 노드를 삭제 후 위치를 바꿔주면 된다.

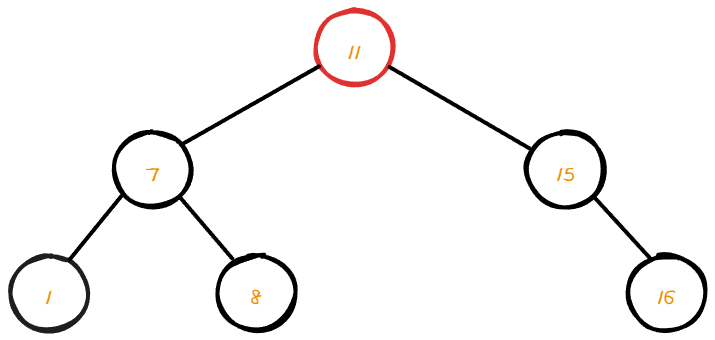
당시 가지고 있던 기술 개념으로 작성된 글 이므로 정확하지 않을 수 있으며 문제가 발견 된다면 수정 하겠습니다.