기존에 사용했던 queue는 단순히 FIFO의 형태를 따른다.
데이터의 우선순위가 들어온 순서에 따라 결정 되는 것이다.

이번에 구현할 queue는 data의 값에 따라 우선순위가 결정되는 priority queue이다.
높은 data값을 가지고 있는 node가 먼저 dequeue된다.

본인은 알고리즘 또는 자료구조 등을 구현할때 Linked List를 사용해서 보통 구현하는 편 이지만 이번에는 Array로 적어볼 것 이다.
이는 priority queue를 heap으로 구현하게 되면 index 계산이 가능하게 되고 접근성도 좋아지게 된다.

구현의 편의를 위해 array의 0번 index는 사용하지 않는다.
array index만으로 부모 자식간의 관계를 정의 한다.

• n번 째 node의 left child node = 2n
• n번 째 node의 right child node = 2n + 1
• n번 째 node의 parent node = n/2

📚 Max Heap

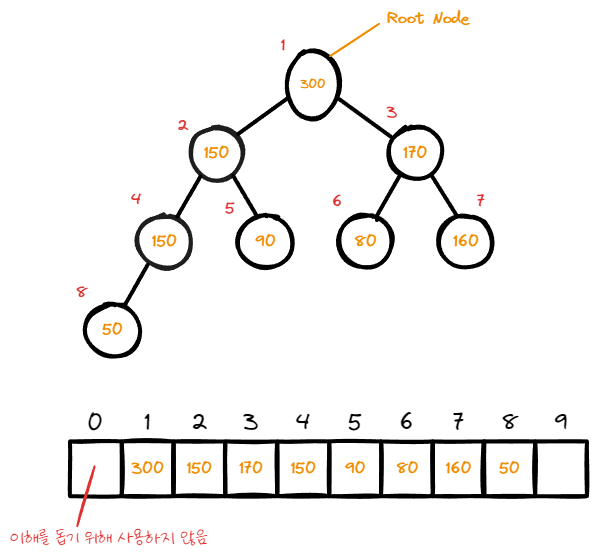
먼저 heap은 크게 두가지의 종류로 분류 된다.
첫번째는 max heap으로 각 node에 저장된 값은 child들에 저장된 값보다 크거나 같다.
결국 root node에 저장된 값이 가장 큰 값으로 설정 되는 것 이다.

max heap으로 구현하는 priority queue는 가장 큰 숫자를 가지고 있는 node가 최우선 순위를 가지고 있을 것 이다.

📌 Priority queue data enqueue

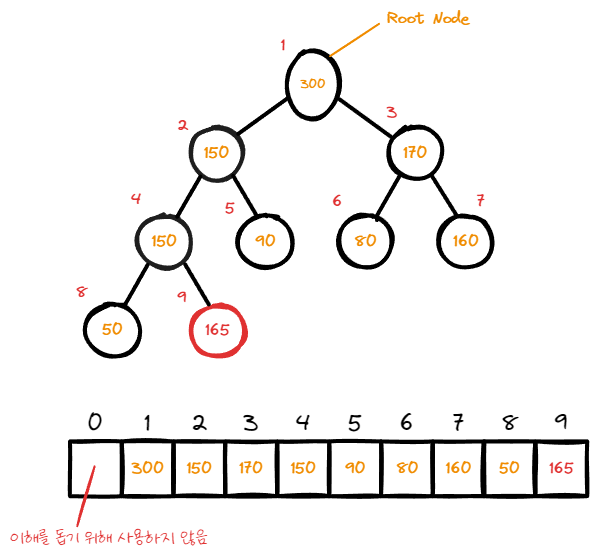
165의 data값을 가지고 있는 node가 추가되었다고 가정해보자.
새로 추가된 node는 무조건 마지막에 추가 된다.
새로 추가된 node는 부모 node의 data값 100보다 크다.
따라서 부모 node와의 swap이 발생한다.

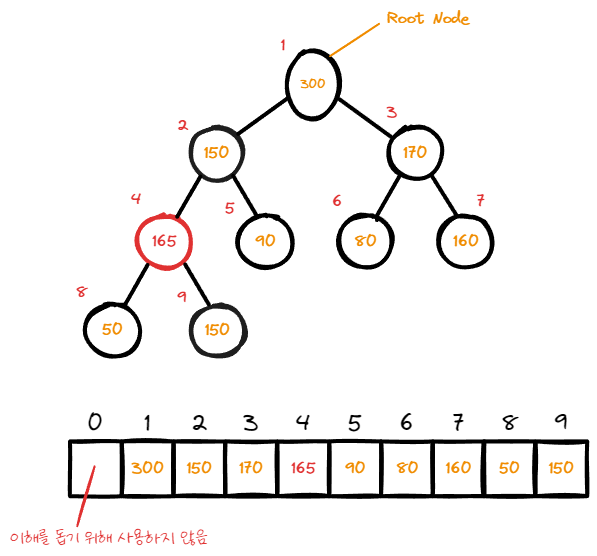
node의 swap이 발생했다. 하지만 여전히 부모의 node보다 data값이 크다.
따라서 부모의 node보다 값이 작지 않을 때 까지 반복해서 swap한다.

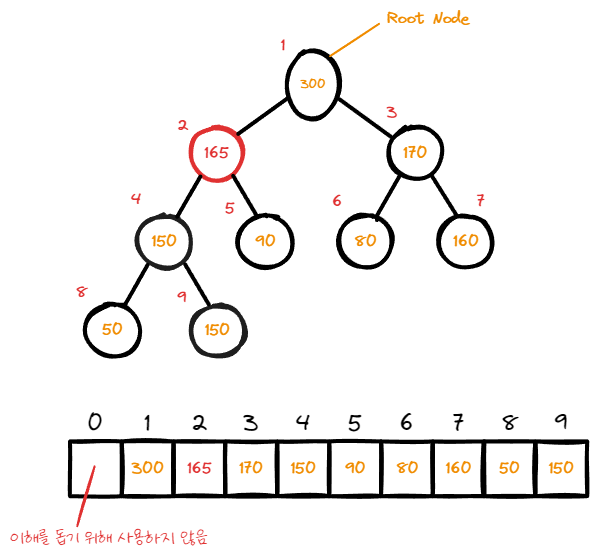
정상적으로 배치가 완료 된 상태이다.

📌 Priority queue data dequeue

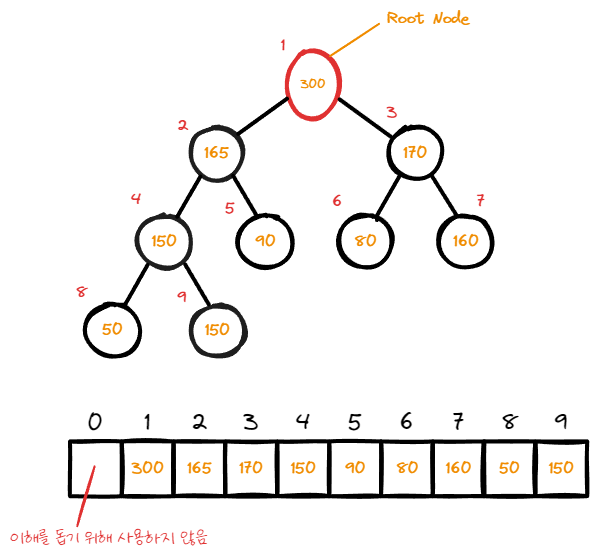
dequeue는 무조건 가장 높은 data 값을 가지는 root node부터 이뤄진다.
node를 삭제 시 무조건 마지막 index의 node가 빈 자리를 대체 한다.

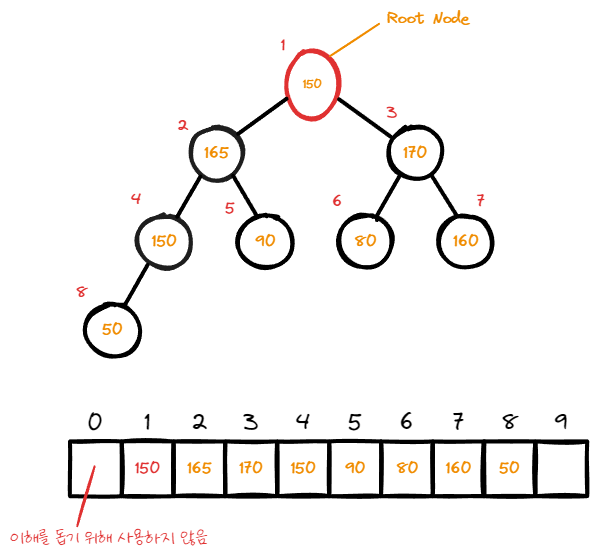
마지막 index의 node가 root node자리를 대체했다. 하지만 자식 node보다 data값이 작은 것을 확인했다.
이때 data값이 가장 큰 자식 node와 swap이 발생 한다.

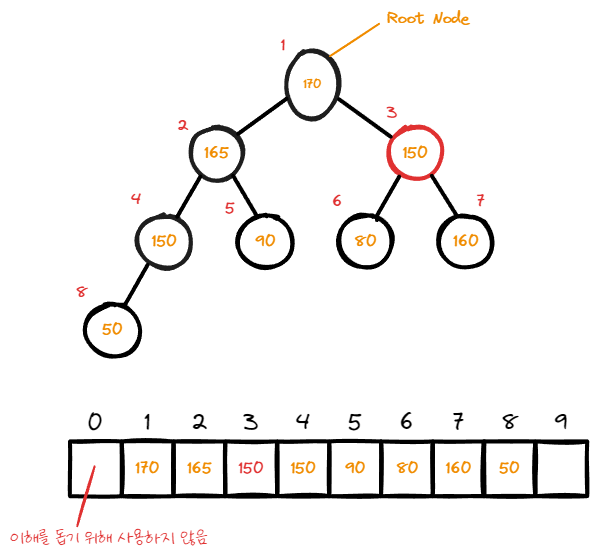
여전히 자식 node보다 data값이 작기 때문에 swap이 발생한다.

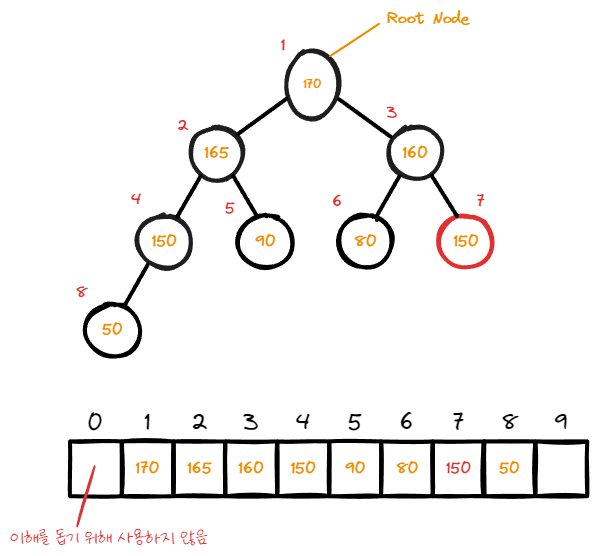
모든 swap이 발생 한후 이어서 root node의 dequeue가 계속 발생 할 것이다.

📚 Min Heap

두번째는 min heap으로 각 node에 저장된 값은 child들에 저장된 값보다 작거나 같다.
결국 root node에 저장된 값이 가장 작은 값으로 설정 되는 것 이다.

동작원리는 max heap과 같으나 부모 node는 자식 node보다 값이 작아야 한다.

📌 Priority queue data enqueue

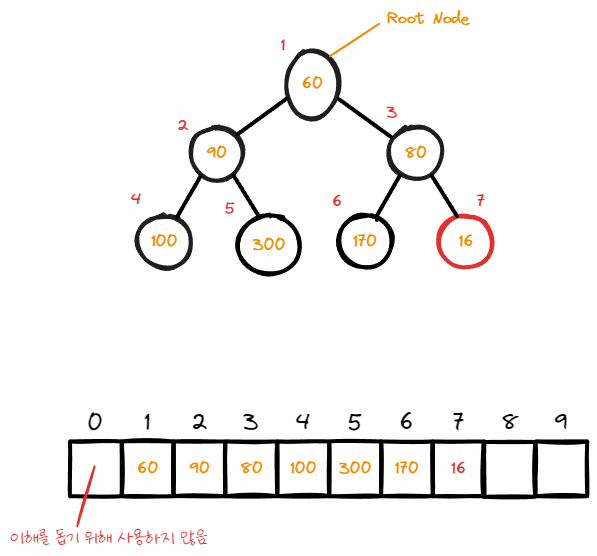
16의 data값을 가지고 있는 node가 추가 되었다.
해당 node는 부모 node의 data값 보다 작기 때문에 min heap에서는 swap의 대상이 될 것이다.

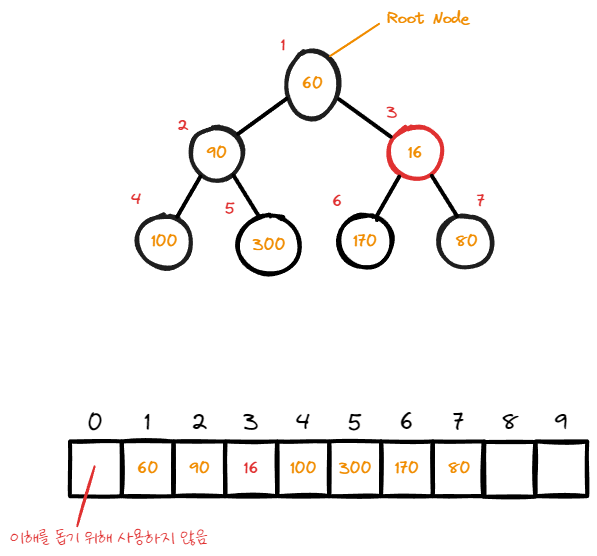
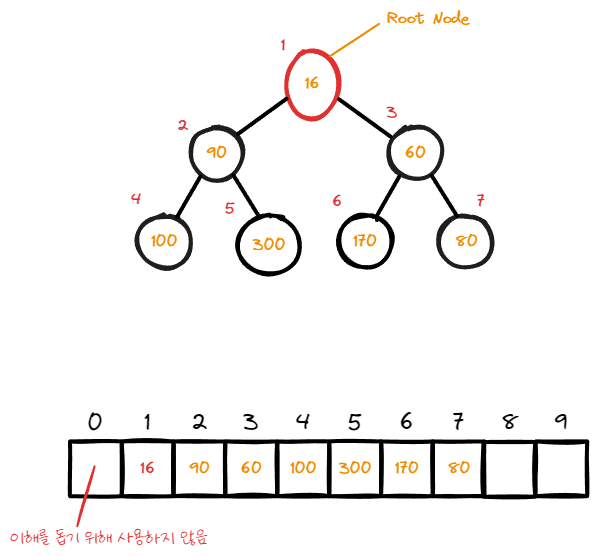
swap 과정을 반복하며 자식 node보다 값이 작을 때 까지 위치를 찾아간다.
위 그림에서는 root node에 위치 함으로써 가장 작은 값 임을 알 수 있음.

📌 Priority queue data dequeue

위 그림에서 dequeue가 발생한다면 가장 작은 data값을 가지고 있는 root node가 target일 것 이다.

해당 root node의 빈자리를 마지막 index node가 대체 할 것이다.

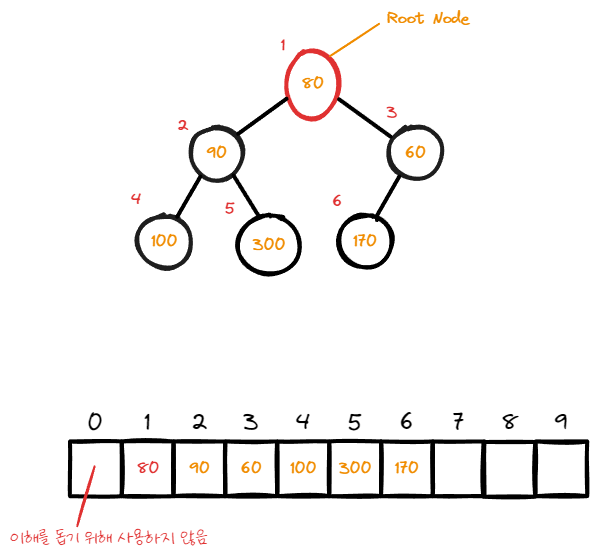
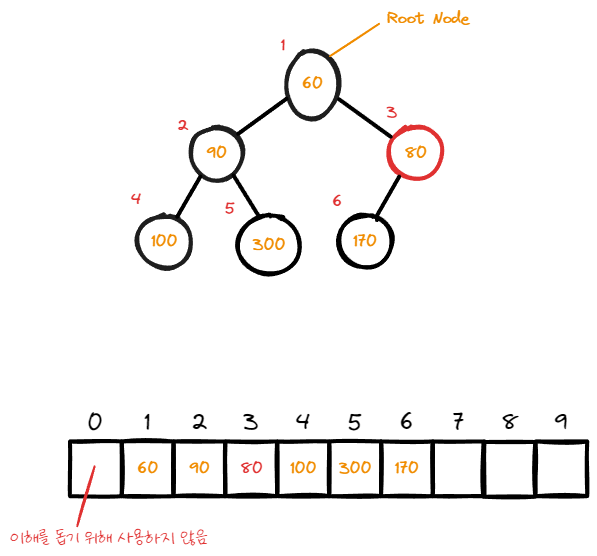
7번 index의 node가 root로 이동한 모습이다.
자식 node의 값을 비교 하여 자식보다 값이 크다면 swap한다.
위 그림에서는 2번, 3번 index의 data값을 비교하며 값이 작은 3번 index와 swap이 발생 한다.

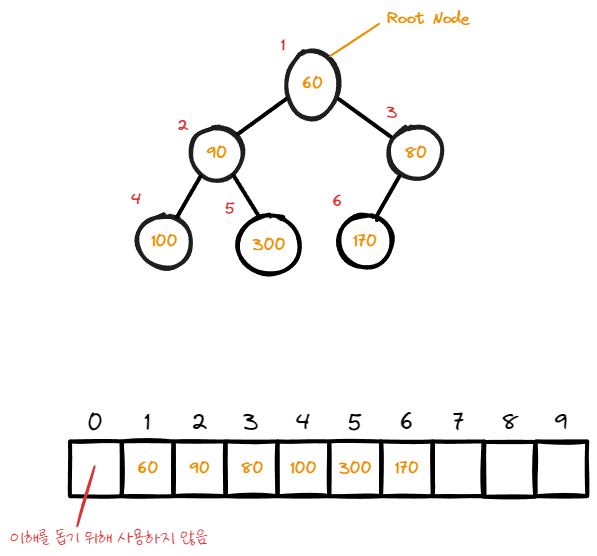
정상적으로 모든 swap이 끝 마쳐친 min heap의 모습을 확인 할 수 있다.
해당 dequeue를 모든 node를 반복하며 data를 출력하면 작은 값부터 차례로 data가 출력되는 priority queue를 구현 할 수 있다.

📗 정리

Heap을 사용해서 priority queue를 만드는 방식을 간단하게 정리 해봤다.
글에서는 min, max 값으로 우선순위를 갖는 heap을 구현 했지만 상황에 따라 다르게 우선순위를 적용한다면 적절하게 사용 할 수 있을 것 같다.

Array 자료구조를 활용해서 priority queue를 구현 하면 부모 node와 자식 node를 index값 계산이 쉬워지기 때문에 구현 역시 편리하다.

heap tree의 높이는 logN이며 push, pop 했을 때 swap하는 과정이 최대 logN번 반복된다.
따라서 시간복잡도는 O(logN)이다.

당시 가지고 있던 기술 개념으로 작성된 글 이므로 정확하지 않을 수 있으며 문제가 발견 된다면 수정 하겠습니다.