Def

A graph G = (V, E) : finite set of vertices V and finite set of edges E.

Properties

• V, E는 집합이므로 V에 속한 각 v와 E에 속한 각 e는 unique하다.
• Edge : (u, v), u와 v는 V에 속한 vertices.
• Vertices와 Edges는 elements를 가지고 있을 수 있다.

Basic Defs in Graph

Undirected graph

• Graph with undirected edges.
• (u, v) = (v, u).

Directed graph

• Graph with directed edges.
• (u, v) != (v, u)
• The first vertex is the origin and the second vertex is the destination.

Sparse graph

• Graph with few edges.
• E = O(|V|), where | | denotes the # of elements in a set.

Dense graph

• Graph with many edges : |E| = O(|V|^2)

Terminology

• End vertices (or endpoints) of an edge
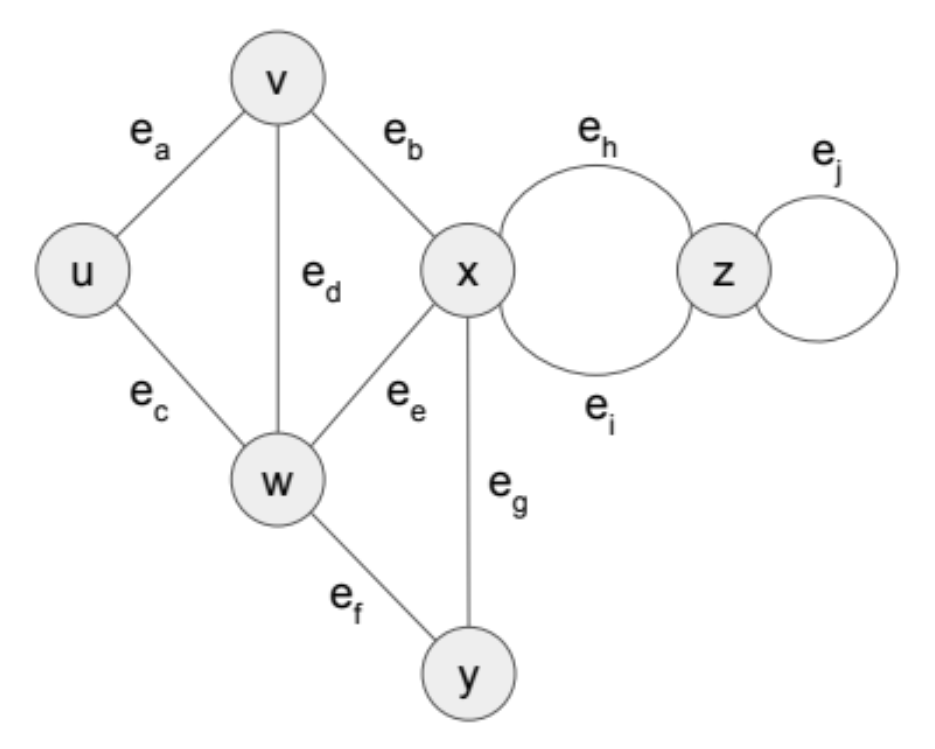
  ex) u and v are the endpoints of e_a
• Edges incident on a vertex
  ex) e_a, e_b, and e_d are incident on v.
• Adjacent vertices
  ex) (u, v) edge 존재 = Vertices u and v are adjacent.
• Degree of a vertex
  ex) Number of incident edges, deg(x) = 5
• Self-loop
  ex) Edge between the same vertex, e_j is a self-loop
• Path : edge들로 연결된 vertices들의 연속.
  length of a path : # of edges on the path.
  The length of the path from a vertex to itself is 0.
• Simple path : Path such that all its vertices and edges are distinct.
  ex) p1 = (v, x, z)
  ex) Non-simple path : p2 = (u, w, x, y, w, v)
• Cycle
  No backtracking
• Simple cycle : 모든 vertices와 edges가 distinct.
  ex) c1 = (v, x, y, w, u, v)
• Non-simple cycle : 같은 노드를 여러번 방문하는 사이클.
  ex) c2 = (u, w, x, y, w, v, u)

Terminology in Directed Graph

• Adjacency
  출발점 노드를 기준으로 생각한다.
  ex) v -> w

표현	Correct?	설명
w is adjacent to v	✔️ 맞음	adjacency list 기준 정의
v is adjacent to w	❌ 틀림	그건 w → v 일 때만 맞음
w is adjacent from v	⚠️ 개념적으로는 가능하지만 거의 사용하지 않음	학술 문헌에서 거의 안 씀

• Degree
  • Indegree : # of incoming edges
    ex) deg_in(x) = 2
  • Outdegree : # of outgoing edges
    ex) deg_out(w) = 2
  • Path and Cycle should be considered with the direction of edges.
• Directed Acyclic Graph (DAG) : Directed graph with no cycles

---

Connectivity

• Subgraph
  A graph S = (V_s, E_s) is a subgraph of G = (V, E) if and only if V_s -> V and E_s -> E.
• spanning subgraph
  contains all the vertices of the original graph (V_s = V)
• Connected graph
  There's a path from every vertex to every other vertex.
• Connected component
  Maximal connected subgraph, 연결되어 있는 정점들 중에서,
  다른 정점을 더해도 연결된 상태를 유지할 수 없는 ‘가장 큰 연결 덩어리’
• complete graph
  There's an edge between every pair of vertices.

Connectivity in Directed Graph

• Strongly connected graph
  There's a path from every vertex to every other vertex.
• Weakly connected graph
  There's a path from every vertex to every other vertex, disregarding the direction of the edges.

Trees and Forests

Trees

A (free) tree is an undirected graph T such that

• T is connected.
• T has no cycles.
• This definition of tree is different from the one of a rooted tree.
• 정점이 N개면 간선은 항상 N−1개를 가진다

Forest

A forest is an undirected graph without cycles.

• The connected components of a forest are trees.
• Cycle(사이클)이 전혀 없는 그래프. 즉, 여러 개의 트리(tree)가 모여 있는 그래프.

Spanning Tree

A spanning subgraph that is a tree.
그래프의 모든 정점을 포함하면서, 사이클 없이 연결된 “트리 형태”의 부분 그래프.

Spanning Forest

• A spanning subgraph that is a forest.
  Disconnected graph에서 찾는 “각 연결 요소별 spanning tree들의 묶음”이 spanning forest이다.

그래프가 connected(연결)이면 → spanning tree가 존재한다.
그래프가 disconnected(비연결)이면 → spanning tree가 없다.
대신 각 연결 요소마다 spanning tree를 만들면 → spanning forest가 된다.

즉, 모든 정점 포함 + 사이클 없음 + 각 컴포넌트 연결성 유지 → spanning forest.