Computer Science Basics
1.Alg & DS study plan

SWEA 기준Algorithm 총 17개Data Structure 총 10개목표 : 1월 12일까지 위 파트 숙지 및 각 항목별 중복 포함 문제 10개 이상씩 풀기 -> 최대 270문제DS : Stack, Queue, Linked List, Priority QueueA
2.Stack

왜 굳이 리턴값을 value라는 매개변수에 간접적으로 리턴하는가? 리턴값과 실제 데이터값을 분리하기 위함. 보통 pop이 불가능한 경우(stack이 비어있을 경우)에 -1같은 sentinel 값을 쓰긴 하지만, 실제로 -1이라는 값이 엄연히 사용되는 수일 수도 있다.
3.Queue

C++ 스타일로 Queue를 구현해보고, Java 스타일로도 구현해보면서Abstract Data Type이라는 게 무엇인지 더 감이 확실히 왔다.강의 자료에서 보면 Queue ADT는Data : 'stores sequence of ordered elements(?)'라
4.Dynamic Programming

큰 문제를 같은 구조의 작은 문제로 쪼개서, 그 답을 저장해 두고 재활용한다!1\. 점화식(재귀 관계) 세우기. \- ex) dp\[i] = dp\[i-1] + dp\[i-2]2\. Memoization(저장) \- 이미 계산한 값은 배열이나 표에 저장. \- 다
5.C++ gdb 터미널 출력 버그

이런 식으로 std::ios::sync_with_studio(false)와 std::cin.tie(nullptr)를 사용하면 잘 나온다.std::ios::sync_with_studio(false): C와 C++ 입출력 버퍼 동기화 해제 -> cin/cout 속도 향상.
6.DS Recap (Array ~ Stack)

Abstract Data TypeA mathematical model of the data objects that make up a data type as well as the functions that operate on these objects.Defined ind
7.DS Recap (Queue, Recursion )

rear(back)에서 Enqueue, front에서 Dequeue가 일어나는 ordered list.FIFO schemeTypically implemented with array or LLenqueue(Object) from rearObject dequeue() fr
8.DS Recap (Sorting by 비교)

(n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2 ~ O(n^2)Best case : O(n) by flagWorst case : O(n^2)Average case : O(n^2)Best case : O(n^2)Worst case : O(n^2)Av
9.DS Recap (sorting by D & C)

Strategy > - Break down into smaller problems > - Solve the smaller problems > - Combine results > - Recursive Sorting via divide-and-conquer Merge S
10.DS Recap (Hash ~ Heapsort )

get(key)put(key, value)remove(key)size()isEmpty()entrySet()keySet()values()put : O(1), but if uniqueness needed, O(n).get, remove : O(n) in the worst
11.DS Recap (DP - MCM, 0-1 Knapsack)
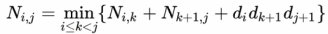
Divide the problem into a nnumber of subproblemsConquer the subproblems by solving them recursively. If the subproblem sizes are small enough, just so
12.DS Recap (DP - LCS)
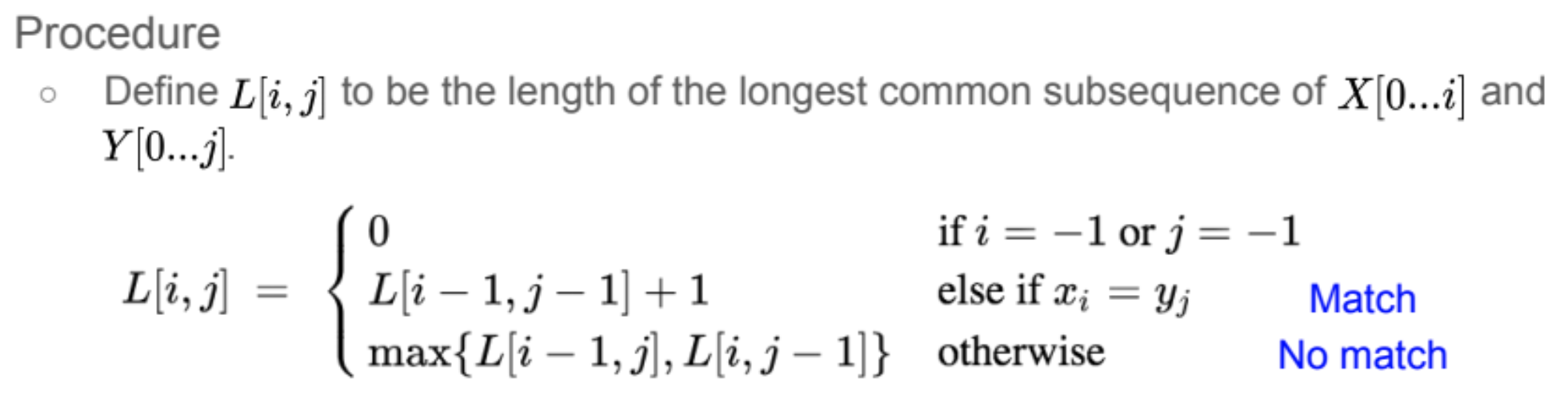
.
13.DS Recap (Graph1)
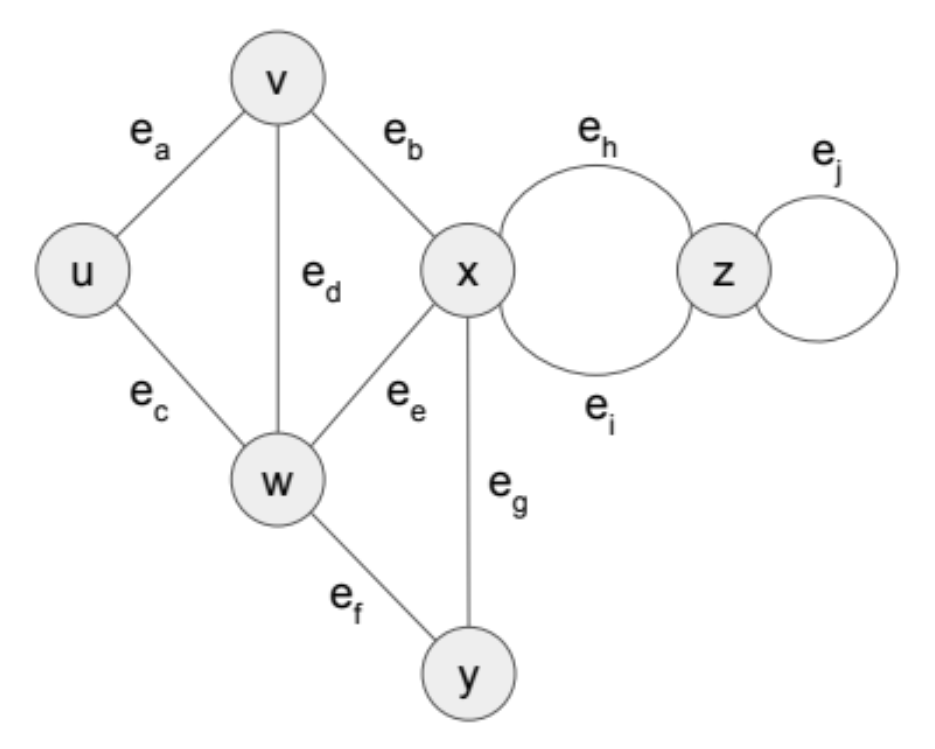
A graph G = (V, E) : finite set of vertices V and finite set of edges E.V, E는 집합이므로 V에 속한 각 v와 E에 속한 각 e는 unique하다.Edge : (u, v), u와 v는 V에 속한 vertices
14.DS Recap (Graph2)
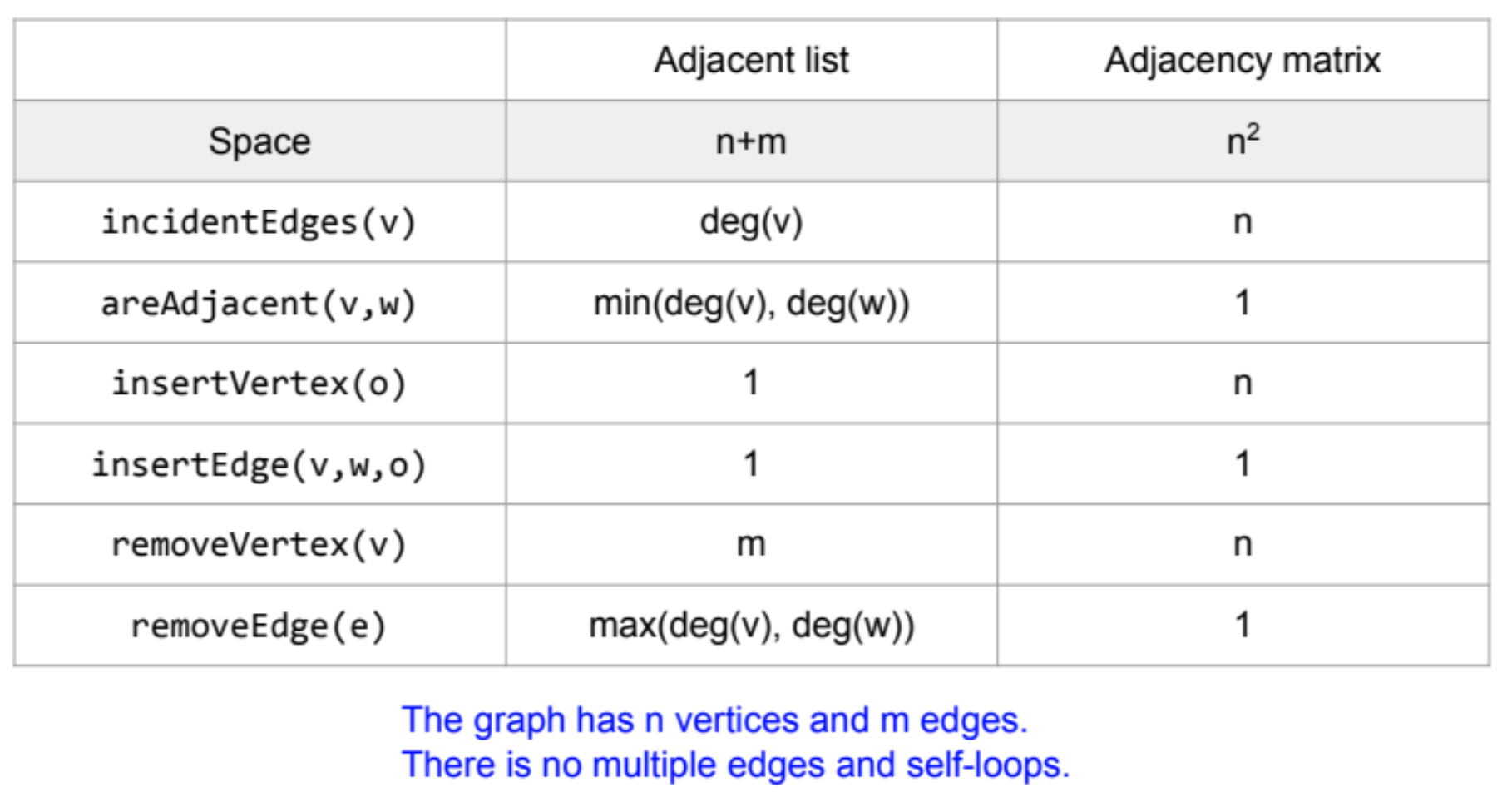
Vertices and edgesendVertices(e) : an array of two endvertices of e.opposite(v, e) : the vertex opposite of v on e.areAdjacent(v, w) : true if and onl
15.DS Recap (Graph3)

Subgraph that contains all vertices of the original graph and is a tree.즉, 기존 그래프의 모든 노드들을 최소한의 엣지로 연결한 그래프. 사이클 X.ST는 여러 그래프를 가질 수 있다.ST중에서 각 edge we
16.DS Recap (Graph4)

Find the shortest path from a starting vertex to all other vertices.The graph is connected.The edge weights are nonnegative.처음 노드에서부터 'cloud'(이미 start
17.C++ 심폐소생기

Call-by-Value vs Call-by-Reference Call by Value : 단지 인자의 값이 사용됨. Call by Reference : 인자는 변수이고, 온전한 변수가 사용됨. 메모리 주소 직접 접근. Overloading 같은 함수 이름으로 두
18.[C++] sort, &, *, ->, ., pq 분해

events.begin(), events.end() : 정렬할 구간(벡터 전체)\[](const auto& a, const auto& b) { ... } : 비교 함수(Comparator)std::sort는 내부에서 원소 두 개 a, b를 꺼내 a가 b보다 앞에 와야
19.Parametric Search (매개변수 탐색)

코드 출처 : 삼성 SW Expert Acadamy리본 테이프 K개를 잘라서 길이 L짜리 조각을 N개 이상 만들 수 있는가?모든 리본을 길이 L로 잘랐을 때, 조각을 N개 이상 만들 수 있는 가장 큰 L. 즉, L이 정답이다. 단조성(monotonicity) 을 띄기
20.C++ 심폐소생기

백준 3079번 문제 long long minT = *min_element(times.begin(), times.end()); 이 때 min_element는 ``에 존재하는 함수이며, 가장 작은 원소를 가리키는 iterator이다. 따라서 이 위치가 표시하는 값을 보려