[Silver I] 구간 합 구하기 5 - 11660

문제 링크

문제 설명

N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.

예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

1	2	3	4
2	3	4	5
3	4	5	6
4	5	6	7

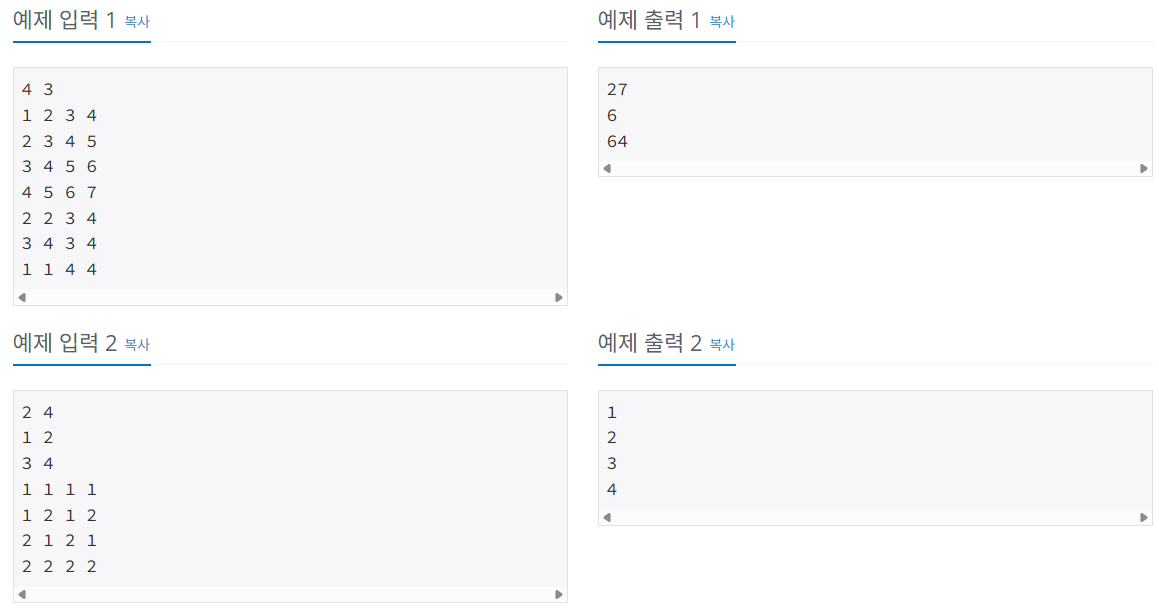
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.

표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.

입력

첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)

출력

총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.

예제

---

✅나의 문제 풀이

public class Main {
    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st = new StringTokenizer(br.readLine());

        //N : 배열 크기, M : 질의 갯수
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

		//인덱스 편의성을 위해 +1
        int[][] A = new int[N+1][N+1];

        //1. 원본 배열 저장
        for(int i=1; i<=N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j=1; j<=N; j++){
                A[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        int[][] D = new int[N+1][N+1];
        //2. 합배열 저장
        for(int i=1; i<=N; i++){
            for(int j=1; j<=N; j++){
                D[i][j] = D[i-1][j] + D[i][j-1] + A[i][j] - D[i-1][j-1];
            }
        }

        //3. 질의 계산 및 출력
        for(int i = 0; i<M; i++){
            //질의 입력받기
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            //구간 합 배열로 질의 계산 하기
            int result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1];
            sb.append(result).append('\n');
        }
        System.out.println(sb.toString());
    }
}

이 문제도 1차원 구간 합배열과 마찬가지로 질의마다 합을 구하면 시간초과로 통과를 못한다.
구간 합배열을 2차원으로도 어떻게 작성하는지 알아보자.

---

✅2차원 구간 합 배열

A[X][Y]는 원본 배열을 의미하며,
D[X][Y]는 원본 배열 A의 (0,0)부터 (X,Y)까지의 사각형 영역 안에 있는 수의 합이다.

먼저 비교적 간단한 1행, 1열을 구해보도록하자.

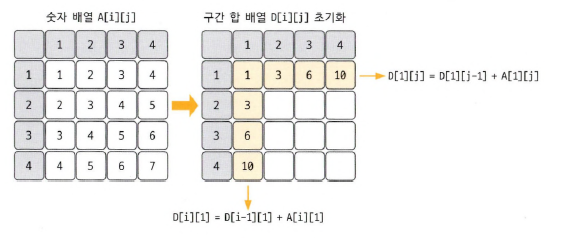
1행 구간 합 구하기

• 위 예시로 1행의 구간 합을 구한다고 생각해보자.
• D[1][3]의 구간합을 구하고 싶다면 바로 직전의 구간 합 + 현재의 값(원본 배열의 A[1][3])을 더해야한다.
• 즉, D[1][3] = D[1][2] + A[1][3] → D[1][3] = 3 + 3 = 6 이 된다.
• 이것을 수식으로 표현하면, D[1][j] = D[1][j-1] + A[i][j] 로 표현 가능하다.

1열 구간 합 구하기

• 마찬가지로 위 예시로 1열의 구간 합을 구한다고 생각하자.
• D[4][1]의 구간 합을 구하고 싶다면 바로 직전의 구간 합 + 현재의 값(원본 배열의 A[4][1]을 더해야한다.
• D[4][1] = D[3][1] + A[4][1] → D[4][1] = 6 + 4 = 10
• 이것을 수식으로 표현하면 D[i][1] = D[i-1][1] + A[i][1]이 된다.

그렇다면 나머지 값은 어떻게 구하지?

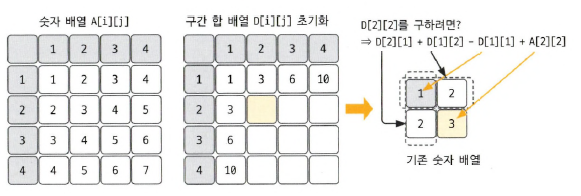
원리만 이해하면 매우 쉽다! 위 1행, 1열을 구한것과 마찬가지로 각각 [i][j-1]과 [i-1][j]를 더하고, 현재의 값(원본 배열의 값)을 더하면 된다.
하지만 이렇게만 하게되면 오차가 생기게된다. 그 이유는 위 이미지와 마찬가지로 겹치는 부분이 생기기 때문이다.(예시에서는 D[1][1]이 겹치는 부분이다) 그래서 이 겹치는 부분을 제거해줘야하는데, 그 수식까지 포함한 공식은 아래와 같다.

D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]