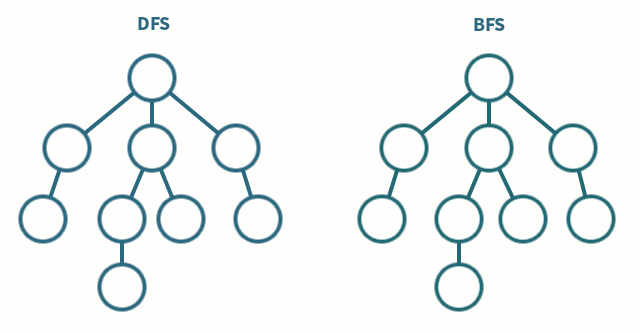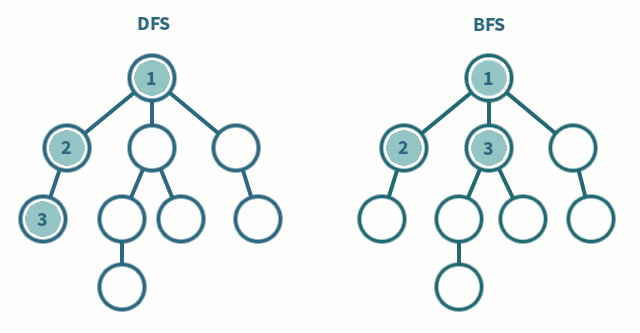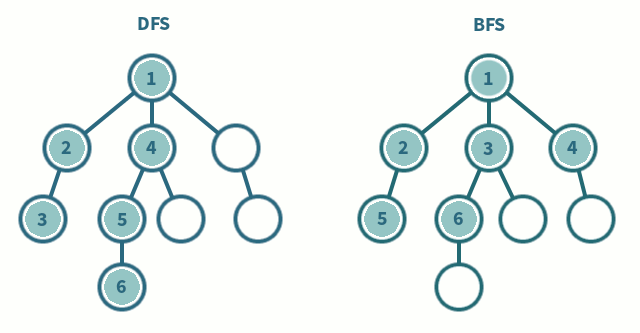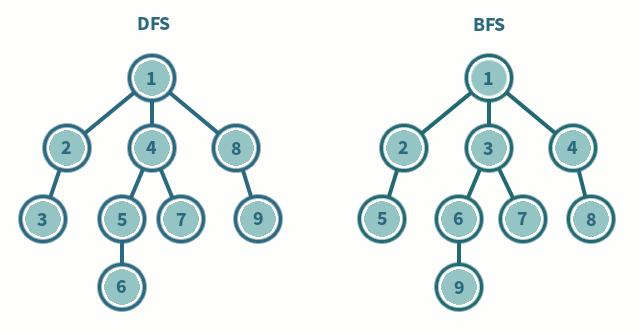
💡DFS(깊이 우선 탐색, Depth First Search)

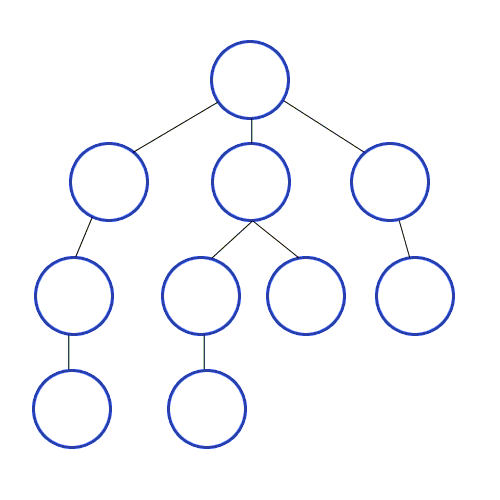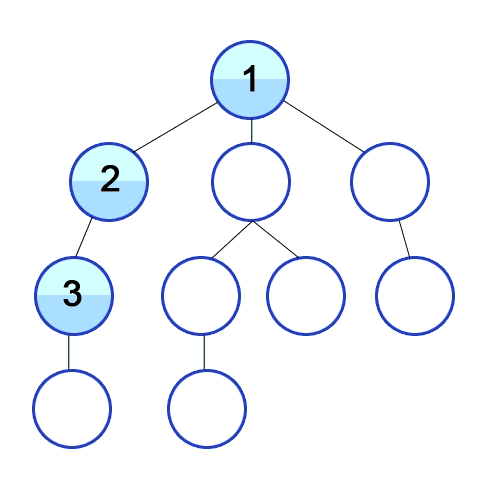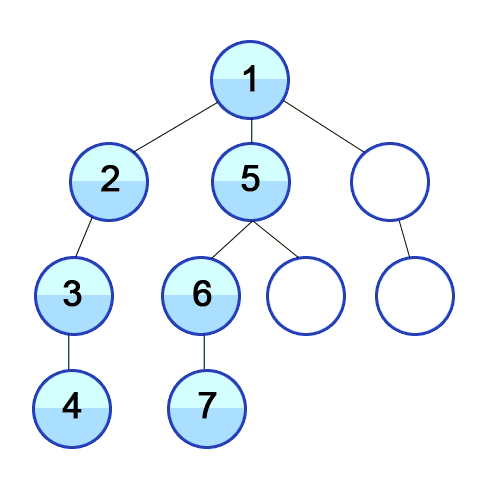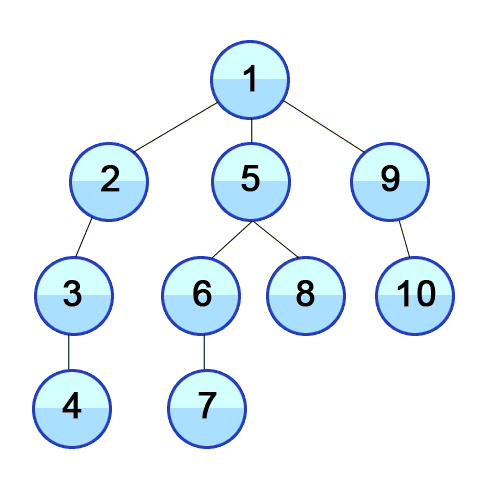
한 경로를 끝까지 따라가다가 더 이상 진행할 수 없으면 되돌아와 다른 경로를 탐색하는 방식

• 구현 : 스택(재귀 호출 or 명시적 스택)
• 시간 복잡도
  - 인접 리스트 : O(V+E) (V:접점, E: 간선)
  • 인접 행렬 : O(V^2)
• 활용
  - 경로 존재 여부 확인
  • 미로 탐색
  • 백트래킹
  • 위상 정렬, 사이클 탐지
• 모든 노드를 방문하는 경우 사용
• BFS(너비 우선 탐색)보다 간단
• 검색 속도 자체는 BFS(너비 우선 탐색)에 비해 느림

---

💡BFS(너비 우선 탐색, Breadth First Search)

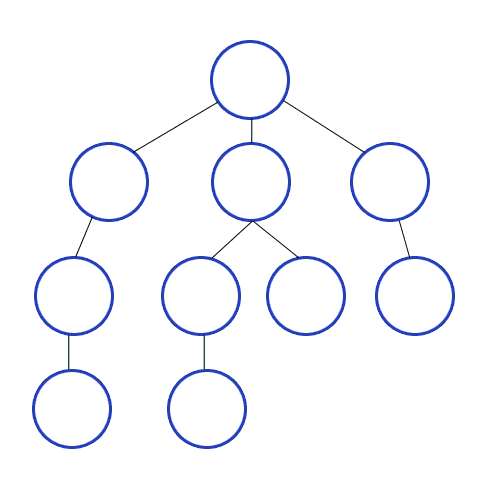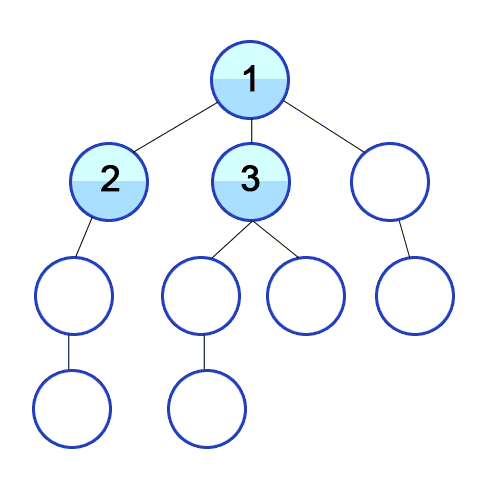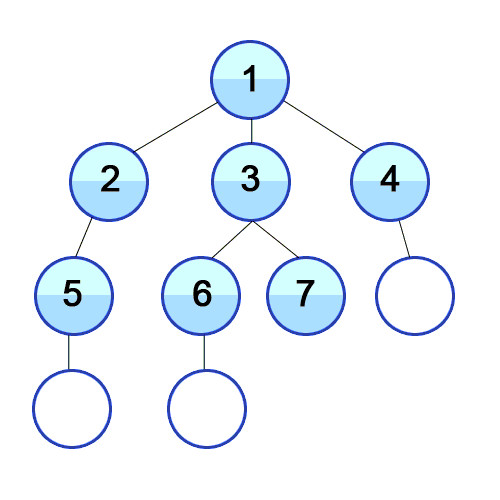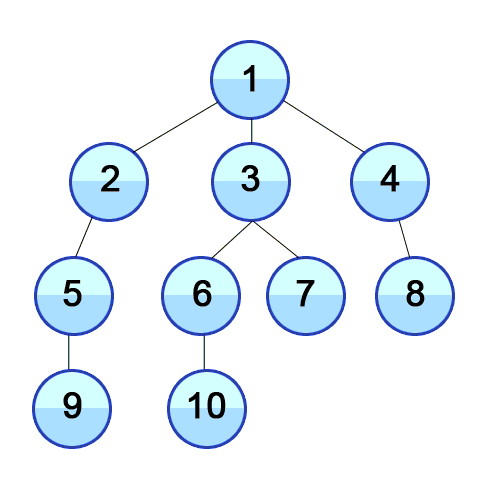
시작점에서 가까운(인접한)노드부터 차례로 탐색

• 구현 : 큐
• 시간 복잡도
  - 인접 리스트 : O(V+E) (V:접점, E: 간선)
  • 인접 행렬 : O(V^2)
• 활용
  - 최단 거리 탐색(가중치 없는 그래프)
  • 네트워크 탐색(친구 추천, 최단 경로...)
  • 레벨 단위 탐색(트리의 레벨 순회, 최단 단계 찾기)
• 모든 노드를 방문하는 경우 사용

---

☑️정리

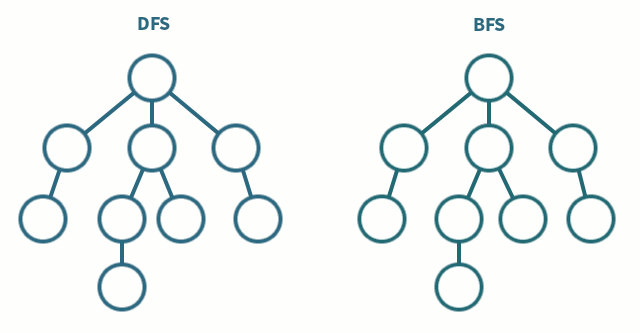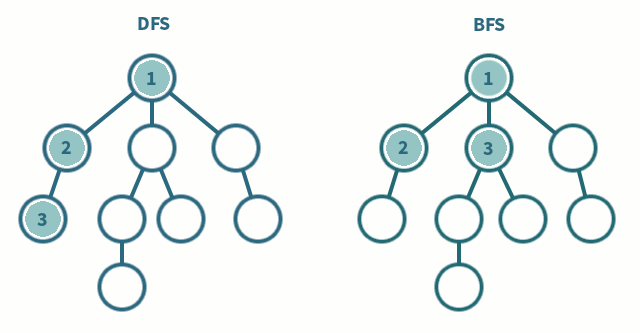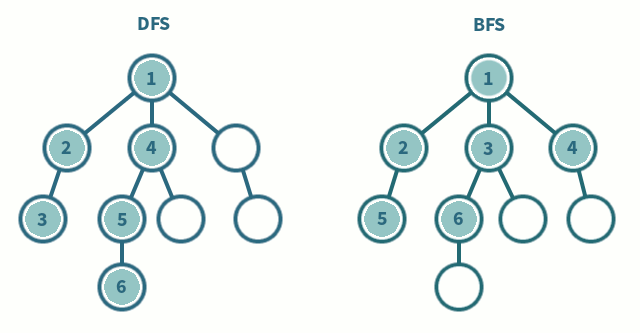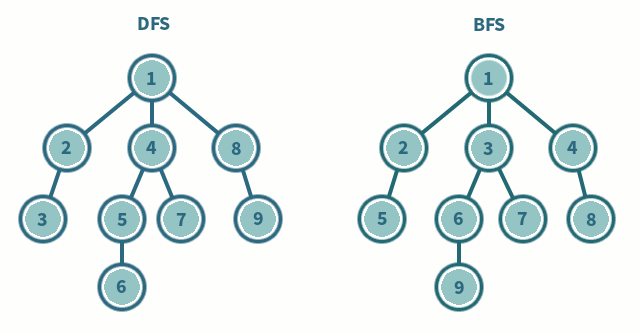
DFS(깊이 우선 탐색)	BFS(너비 우선 탐색)
한 경로를 끝까지 따라가다가 다른 경로를 탐색	시작점에서 가까운 노드부터 탐색
스택 또는 재귀함수로 구현	큐를 이용해서 구현

---

🎯백트래킹(Backtracking)

• 정의 : 모든 경우의 수를 탐색하면서, 조건에 맞지 않으면 중간에서 탐색을 포기하고 되돌아가는 방식
• 탐색 최적화 기법 : 불필요한 경로를 가지치기 해서 탐색 범위 축소
• 구현 : 보통 DFS(재귀)와 함께 사용

⚖️가중치(Weight)

• 정의 : 그래프에서 간선에 붙는 비용/거리/시간 같은 값을 의미
• 가중치 있는 그래프 : 모든 간선의 비용이 동일(예 : BFS로 최단거리 가능)
• 가중치 있는 그래프 : 간선마다 비용이 다름 → BFS만으로는 최단거리 못 구함.

🚀다익스트라 알고리즘(Dijkstra)

• 정의 : 가중치가 있는 그래프에서 한 정점 → 모든 정점까지의 최단 경로를 구하는 알고리즘
• 원리
  1. 출발 노드부터 시작
  2. 방문하지 않는 노드 중 가장 짧은 거리를 선택
  3. 그 노드를 거쳐 다른 노드로 가는 경로를 갱신
  4. 모든 노드를 방문할 때까지 반복
• 시간 복잡도
  - 기본 구현 : O(V^2)
  • 우선순위 큐(힙) 사용 : O(E log V)

---

💡 면접 예상 질문

1. DFS와 BFS의 차이를 설명해보세요.

• DFS는 깊이 우선 탐색으로, 한 경로를 끝까지탐색 후 되돌아오는 방식이며, BFS는 가까운 노드부터 탐색하는 방식입니다. DFS는 경로 탐색, 백 트래킹에 유리하며 BFS는 최단거리 탐색에 유리합니다.

2. BFS가 최단 경로 탐색에서 유리한 이유는 무엇인가요?

• BFS는 시작점에서 가까운 노드부터 차례로 탐색하기 때문에 가중치가 없는 그래프에서는 처음 도착한 경로가 곧 최단 경로가 됩니다.

3. DFS가 BFS보다 더 적은 메모리를 사용할 수 있는 상황은 언제인가요?

• 그래프의 가지 수가 많고 깊이는 얕은 경우 DFS는 깊이만큼만 저장하면 되므로 BFS보다 메모리를 적게 씁니다. BFS는 같은 레벨의 모든 노드를 큐에 저장해야 하므로 메모리 사용이 커질 수 있습니다.

4. 그래프가 깊고 가지 수가 많을 때 DFS의 단점은 무엇일까요?

• 한쪽 경로로 깊게 들어가버리면 시간과 메모리를 낭비할 수 있고, 재귀로 구현할 경우 스택 오버플로우 위험이 있습니다.

5. BFS를 재귀로 구현할 수 있을까요?

• 가능은 하지만 BFS는 큐 자료구조 기반이라 재귀보다는 반복문과 큐로 구현하는것이 직관적이고 일반적이라고 생각합니다.

6. 백트래킹 문제는 보통 DFS로 푸는 이유는 무엇인가요?

• 백트래킹은 경로를 따라가다가 조건에 맞지 않으면 돌아와야 하므로, 한 경로를 끝까지 탐색하는 DFS와 잘 맞습니다.

7. 가중치가 있는 최단 경로 문제에서는 왜 BFS가 아닌 다익스트라 알고리즘을 써야 할까요?

• BFS는 모든 간선 비용이 동일할 때만 최단 경로를 보장합니다. 가중치가 다르면 더 긴 경로라도 비용이 더 작은 경우가 있을 수 있기때문에, 각 간선의 가중치를 고려하는 다익스트라 알고리즘을 사용해야 합니다.