💡힙(Heap)이란?
완전 이진 트리(Complete Binary Tree)를 기초로 하는 자료구조로써, 여러 개의 값중에서 가장 크거나 작은 값을 빠르게 찾기 위해 만든 이진트리이다.
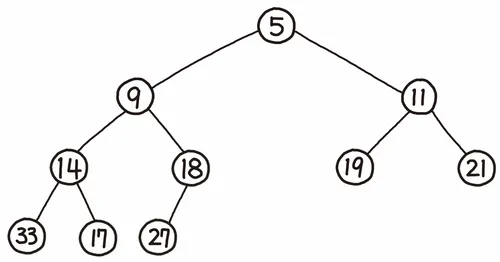
✅힙의 특징
- 힙은 최대힙(Max heap)과 최소힙(Min Heap)으로 나누어진다.
최대힙은 부모노드의 값이 자식노드들의 값보다 항상 크고, 최소 힙은 부모노드의 값이 자식노드의 값보다 항상 작다. - 위 성질때문에 항상 느슨한 정렬상태(반정렬 상태)를 유지한다.
- 힙은 중복값을 허용한다.
- 보통 배열로 구현하며 인덱스로 부모/자식 위치를 계산한다.
✅힙을 배열로 구현하기
힙은 대체적으로 배열로 구현하며, 완전이진트리를 기본으로 하기 때문에 배열로 구현하기에 용이하다.
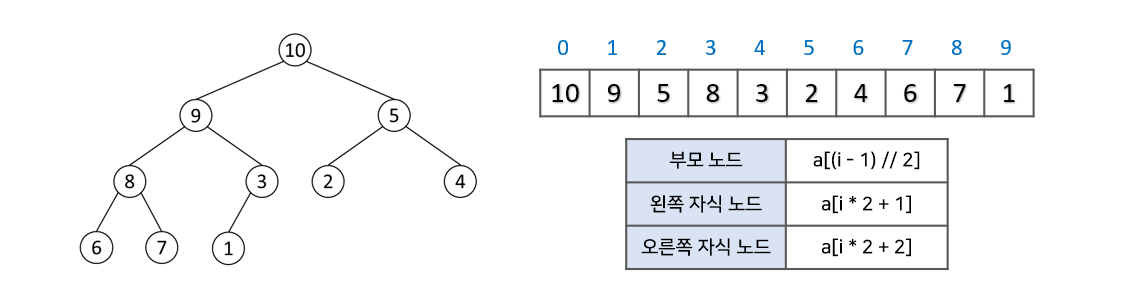
- 루트 노드는 배열의 0번 인덱스에 저장
- 각 노드를 기점으로 왼쪽 자식 노드는 a[i*2+1], 오른쪽 자식 노드는 a[i*2+2]의 인덱스에 저장된다.
- 특정 인덱스의 노드에서 부모 노드는 a[(i−1)//2]로 찾을 수 있다.
✅힙의 데이터 처리(삽입/삭제)
최대힙의 부모노드는 항상 자식노드의 값보다 크고, 최소힙의 부모노드는 항상 자식노드의 값보다 작다는 조건을 가지고 있다.
하지만 힙에서 삽입 또는 삭제가 일어나게 된다면 힙의 조건이 깨질 수 있다. 이러한 경우에 힙의 조건을 만족할 수 있게 노드들의 위치를 바꿔가며 힙의 재구조화(heapify)를 해주어야 한다.
삽입/삭제의 경우 모두 연산 자체는 O(1)이지만, heapify의 과정을 거치기 때문에 O(log n)의 시간 복잡도를 가지게 된다.
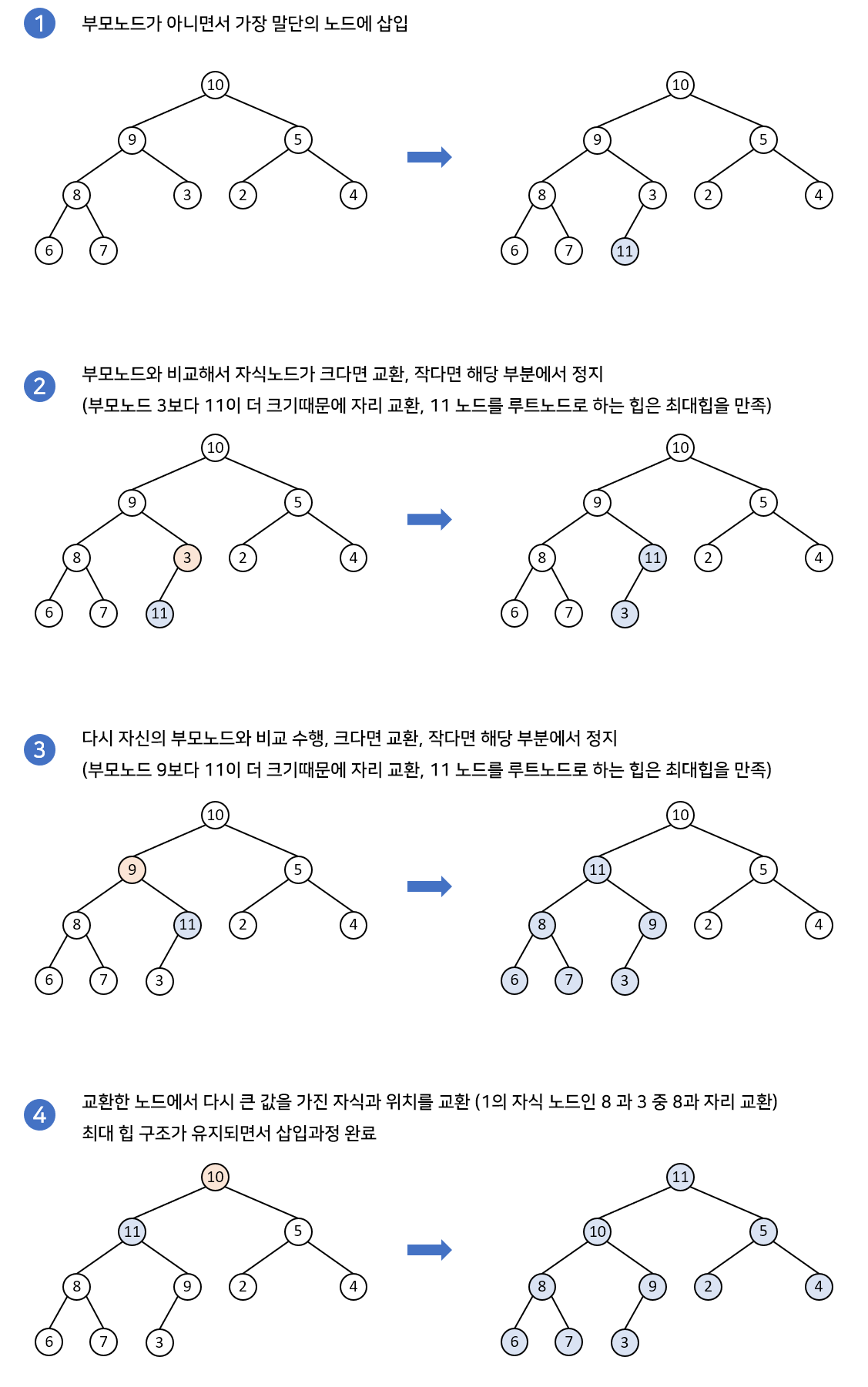
✅데이터 삽입
- 새로운 노드는 리프노드가 아니면서 가장 말단에 있는 노드의 자식 노드로 추가
- 그 노드와 부모 노드를 비교
- 규칙에 맞으면 그대로 두고, 아니라면 부모 자리와 교환
- 규칙에 맞을때까지 반복
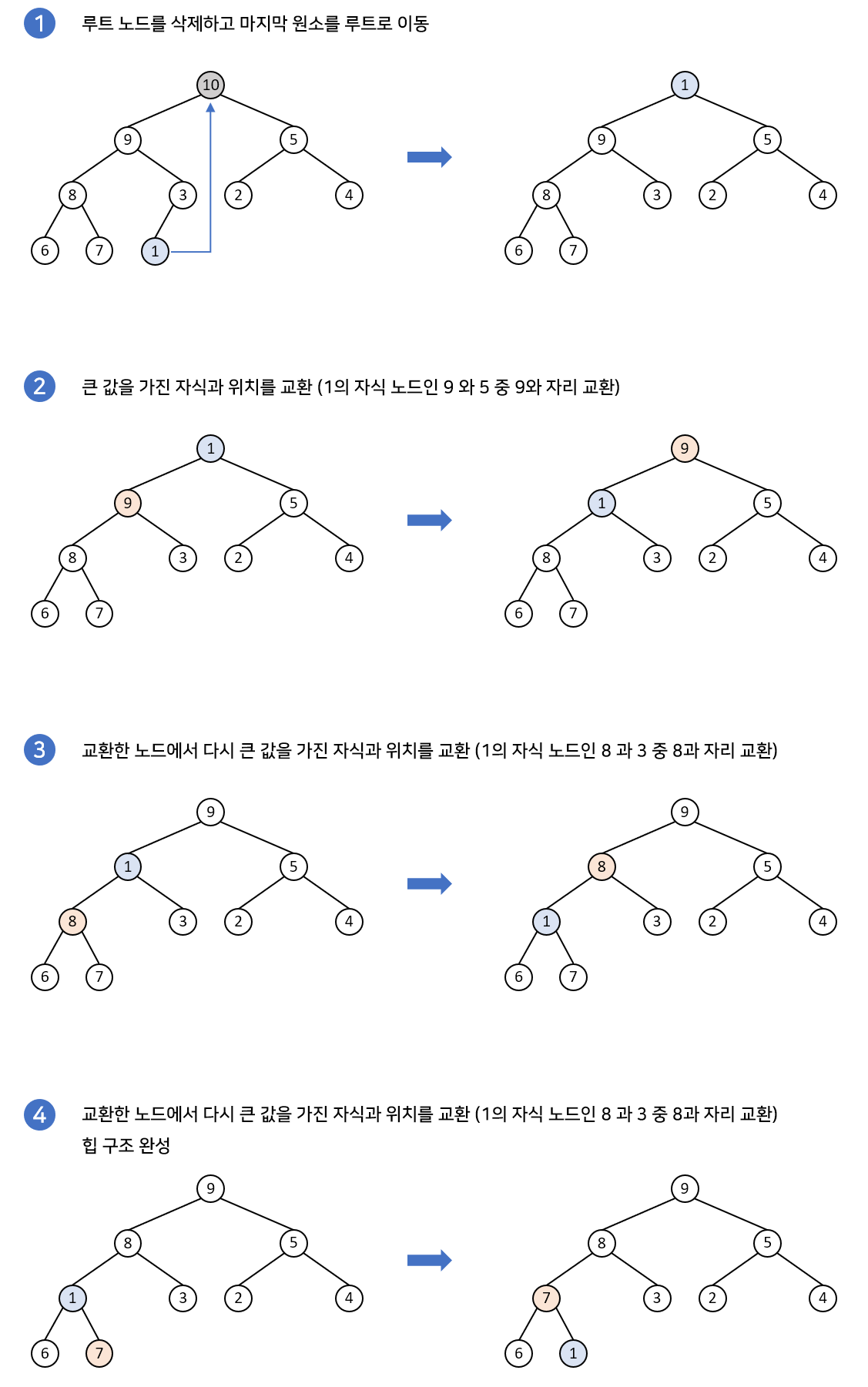
✅데이터 삭제
📌힙의 삭제는 최댓값 혹은 최솟값이 저장된 루트 노드만 제거할 수 있다.
1. 루트 노드를 제거하고, 마지막 원소를 루트로 이동시킨다.
2. 루트로 올라간 노드와 그 자식 노드들을 비교한다.
3. 조건에 만족하면 그대로 두고, 그렇지 않다면 자식과 교환
- 최대힙
1. 부모보다 더 큰 자식이 없으면 교환하지 않고 끝낸다.
2. 부모보다 더 큰 자식이 하나만 있으면 그 자식하고 교환하면 된다.
3. 부모보다 더 큰 자식이 둘 있으면 자식들 중 큰 값과 교환한다.
- 최소힙
1. 부모보다 더 작은 자식이 없으면 교환하지 않고 끝낸다.
2. 부모보다 더 작은 자식이 하나만 있으면 그 자식하고 교환하면 된다.
3. 부모보다 더 작은 자식이 둘 있으면 자식들 중 작은 값과 교환한다.
- 조건을 만족할 때까지 3을 반복
✅힙의 장/단점
👍장점
1. 최댓값/최솟값 탐색이 매우 빠르다(O(1))
힙은 항상 힙 속성을 만족한다.
최대 힙 : 부모 노드의 값은 항상 자식 노드의 값보다 크거나 같음
최소 힙 : 부모 노드의 값은 항상 자식 노드의 값보다 작거나 같음
이 속성 덕분에 힙의 루트 노드는 항상 전체 데이터의 최대값 또는 최솟값을 가리키므로 최댓값/최솟값 탐색 시 O(1)의 시간 복잡도가 걸린다.(즉시 접근 가능)
2. 데이터 추가 및 삭제가 효율적이다(O(log n))
새로운 데이터를 추가하거나 루트 노드를 삭제할 때, 힙은 그 구조를 유지하기 위해 약간의 조정을 거친다. 이 과정은 트르의 높이에 비례하는 시간이 걸리는데, 완전 이진 트리는 항상 균형 잡힌 상태를 유지하므로 데이터가 n개일 때 높이는 log n에 비례한다. 따라서 추가 및 삭제 연산은 O(log n)의 시간 복잡도를 보장한다.
3. 메모리 사용이 효율적이다
힙은 완전 이진 트리 구조 덕분에 배열로 쉽게 구현이 가능하다. 그래서 힙은 포인터를 위한 추가적인 메모리 공간이 없어 매우 효율적이며, 배열의 인덱스만으로 부모와 자식의 노드 관계를 간단히 계산할 수 있다.
👎단점
1. 최댓/최솟값 이외의 값 검색이 비효율적이다(O(n))
힙은 최댓값/최솟값을 찾는데에만 특화되어 있다.
루트노드를 제외한 다른 값들은 정렬되어 있다는 보장이 없으며, 특정 값을 검색하는 데에는 최악의 경우 모든 데이터를 확인해야 하므로 O(n)의 시간복잡도가 소요된다.
2. 임의의 원소 삭제가 어렵다(O(n))
루트 노드가 아닌 중간의 특정 원소를 삭제하려면, 먼저 그 원소를 찾는데 O(n)의 시간이 필요하고 삭제 후 힙 속성을 복구하는 데 추가 시간이 걸린다. 이러한 이유는 힙이 완전 이진 트리 구조를 유지해야 하기 때문이다.
3. 데이터 정렬에 추가적인 작업이 필요하다
힙은 힙 속성을 만족하는 완전 이진 트리 구조의 자료구조일뿐, 힙 자체는 정렬된 구조가 아니다. 힙의 모든 데이터를 정렬 상태로 얻기 위해서는 힙의 루트 노드를 반복적으로 제거하고 힙 구조를 재조정하는 힙 정렬 과정을 거쳐야한다. 이 과정에는 O(n log n)의 시간이 추가로 소요된다.
4. 구조 변경이 복잡하다
힙은 완전 이진트리 구조를 유지해야 하므로 데이터의 추가 및 삭제 시마다 구조를 재조정하는 과정(heapify)이 필요하다. 이 과정이 O(lng n)으로 비교적 빠르긴 하지만, 단순히 데이터를 넣고 빼는 다른 자료구조에 비하면 구조 유지를 위한 추가적인 연산이 항상 동반된다.
💡힙 정렬(Heap Sort)
배열 전체를 힙으로 만든 뒤 루트부터 하나씩 꺼내 정렬하는 방식
- 힙 정렬의 시간 복잡도는 O(n log n)으로 빠른 정렬에 속한다.
- 최악의 경우에 O(N2)의 성능을 내는 퀵 정렬과 달리 항상 O(n log n)정렬의 성능을 발휘한다.
- 추가적인 배열을 사용하지 않아 메모리 측면에서도 이점을 보인다.
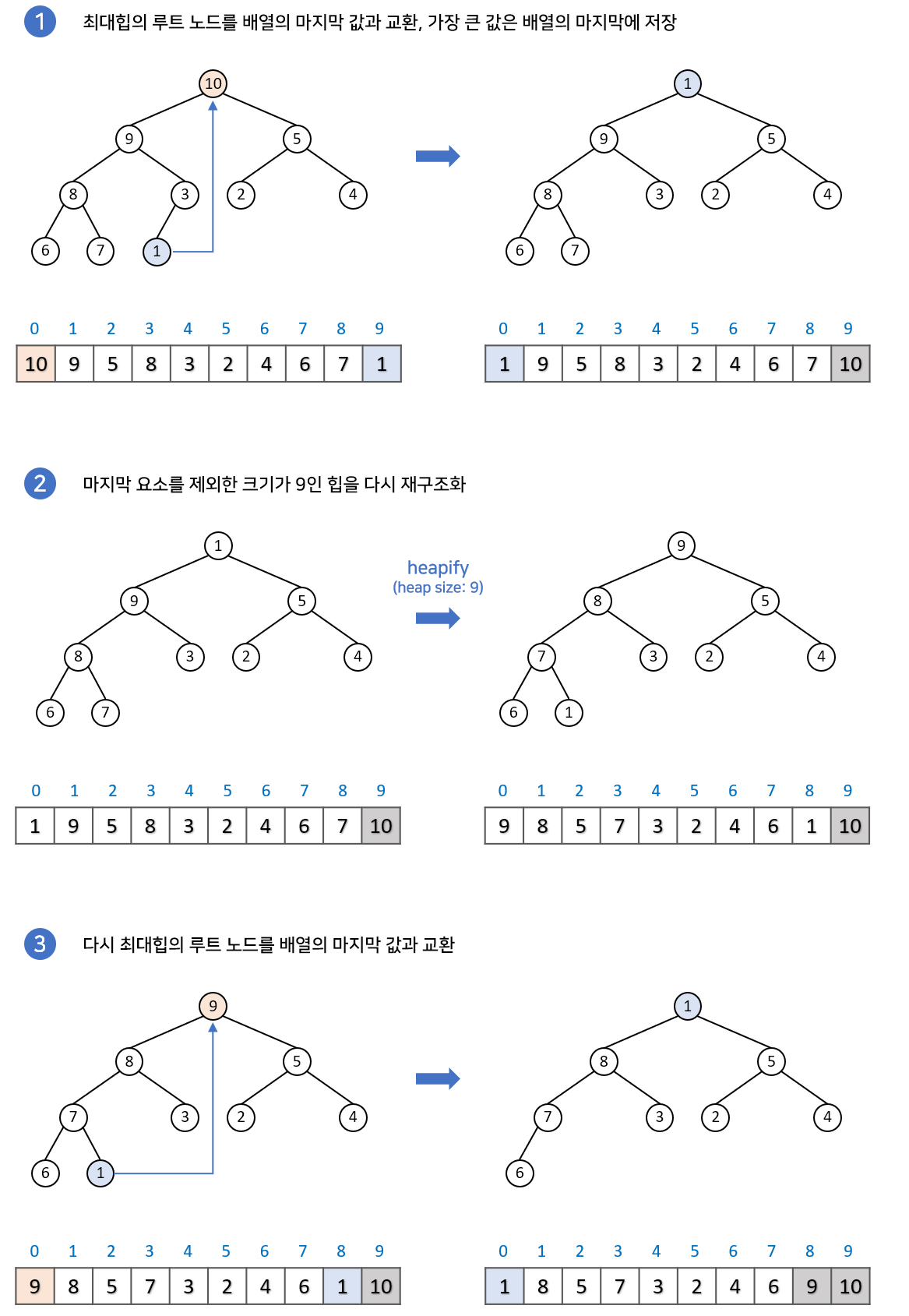
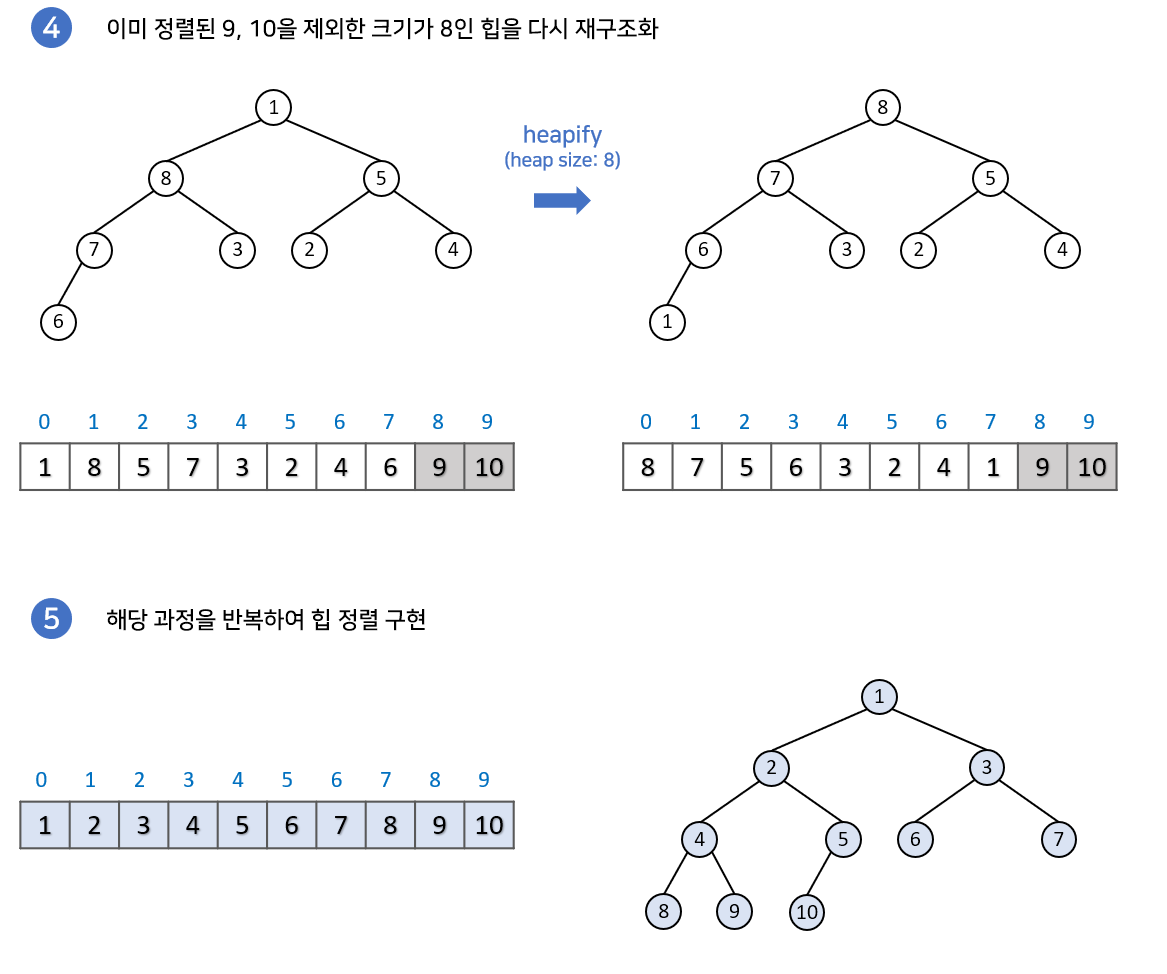
✅힙 정렬의 과정
- 최대 힙을 구현한 뒤, 루트 노드를 삭제하여 배열의 맨 마지막에 넣어주고, 깨진 힙을 재구조화하는 과정을 반복한다.