2160. Minimum Sum of Four Digit Number After Splitting Digits

Problem type - Greedy

🧩 Problem

🎯 Strategy

Greedy Algorithm

To solve this problem, all we should think is that a given number has four digits and should use a greedy method.

Sort and Stringify

When the four digits are in ascending order, the minimum sum of the pair should be the number's
(first and third digit) + (second and last digit)

In order to sort the number, we should change the number into a string first.

def mini..(self, num: int) -> int:
	a = sorted(str(num))

Result

To conclude the previous logic, we should use those numbers by the following:
(Don't forget to change the string into a number to get the sum.)

...
	a = sorted(str(num))
    return int(a[0] + a[1]) + int(a[2] + a[-1])

📌 Thoughts

I thought the problem was asking about combinations, but it turned out it was a simple greedy problem. I should challenge more greedy problems and think in a "greedy" way.

💻 Solution

def minimumSum(self, num: int) -> int:
        a = sorted(str(num))
        return int(a[0] + a[2]) + int(a[1] + a[-1])

876. Middle of the Linked List

Problem type - Linked List

🧩 Problem

🎯 Strategy

Set up the logic

There are two ways to solve this problem. The first approach is the brute force approach, and the second approach is a pointer approach. I will cover both approaches in this post.

Brute Force

To solve this problem in brute force method, we need to understand how this code works. This linked list question's answer should return a middle of the list.

Because it differs from the list, we should iterate over the whole list to get the length of the list (Because all we have is the first node of the list)

Now, we will create the empty list and counter for each head's number.
temp = [], count = 0

Append the current head and increase the count by one. Set the head to the next element. Then, the first loop is done. Iterate over until head.next == None

i is the index number of the temp. There are two cases to get the middle index of the temp list.

As the count is the length of the list, we should use this to get the middle node. There's no clear middle node if the count is an even number. In this case, we take node to the right (2, 3 --> 3), hence index number should length // 2, which is i == count // 2

# count is even number
[1, 2, 3, 4]
temp[2] == 3

If the count is odd number, we can take the middle node. In following case, the length of the list is 5, and five / 2 is 2.5, so we can truncate 0.5, and return index number.

Or simply we can just use i == count // 2

# count is odd number
[1, 2, 3, 4, 5]
temp[2] == 3

def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        temp = []
        count = 0

        while head:
            temp.append(head)
            count += 1
            head = head.next

        i = count // 2 if count % 2 else trunc(count / 2)
        return temp[i]

The time complexity is O(n), and the space complexity is O(n)

Two Pointer

Another way to solve this problem is by using the pointer method.

To provide a better explanation, I have included the following picture:

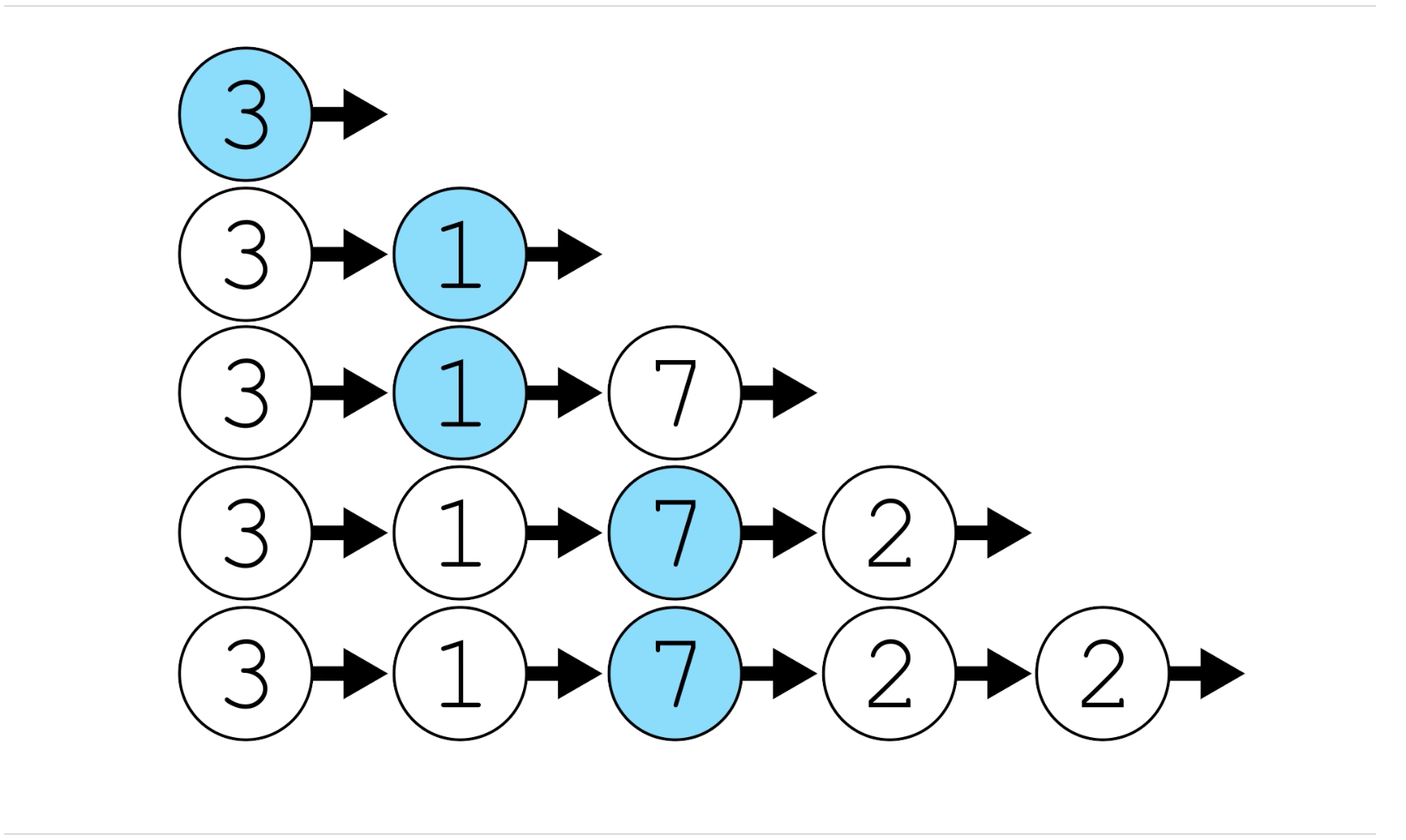
Let's assume that we have two pointers. The pointer one points to the middle node, and the pointer two points to the end node.

One pointing to the middle node and the other to the end node. Initially, both pointers start from the head (indicated by the blue color in the picture).

In the second line of the picture, both pointers move. In the third line, the middle pointer stays at the same node (blue point), and the end pointer moves to node 7.

From this case, we can derive that the middle pointer only moves whenever the size of the list grows by two.

To determine the size of the linked list, we need to iterate until we reach the end. We will iterate this linked list as long as the end pointer has two spaces to jump.

Hence, the endpoint must not be None, and the next node must also not be None(while end and end.next: ) . This means our middle node moves up one node every step, and the end node moves up two nodes every step.

def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        middle = head
        end = head
        
        while end and end.next:
        	middle = middle.next
            end = end.next.next
            
        return middle

The time complexity is O(n) because we need to reverse over at least n over two nodes. The space complexity is constant(O(1)), because for any input size n, we use only two pointers to traverse the list.

📌 Thoughts

This is my first time attempting to solve the linked list problem. Initially, it was hard to understand the concept. However, after some research and studying, I discovered that the pointer method is much more efficient in terms of code writing and space complexity.

💻 Solution

def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        middle = head
        end = head
        
        while end and end.next:
        	middle = middle.next
            end = end.next.next
            
        return middle