2656. Maximum Sum With Exactly K Elements

Problem type - Greedy

🧩 Problem

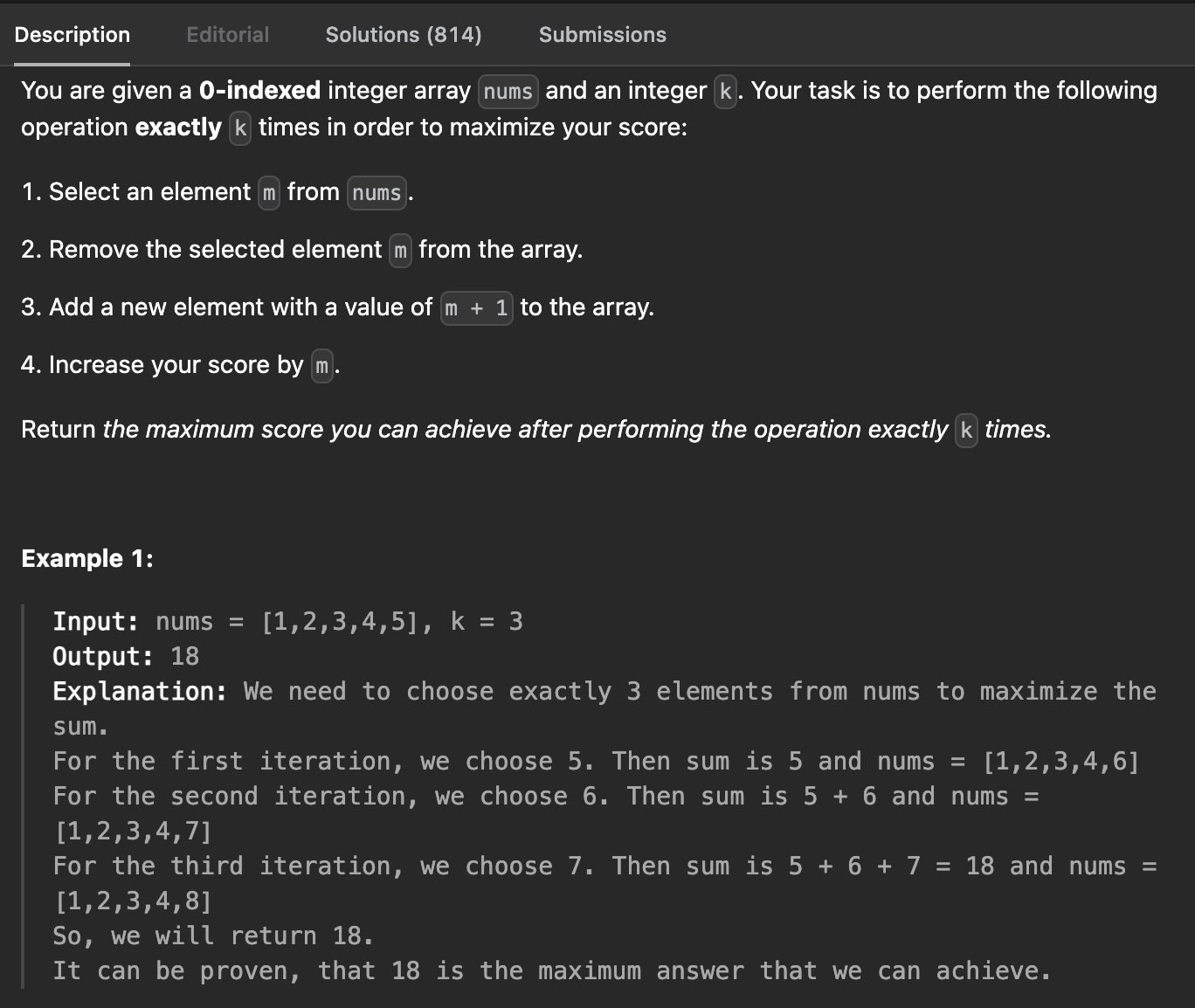
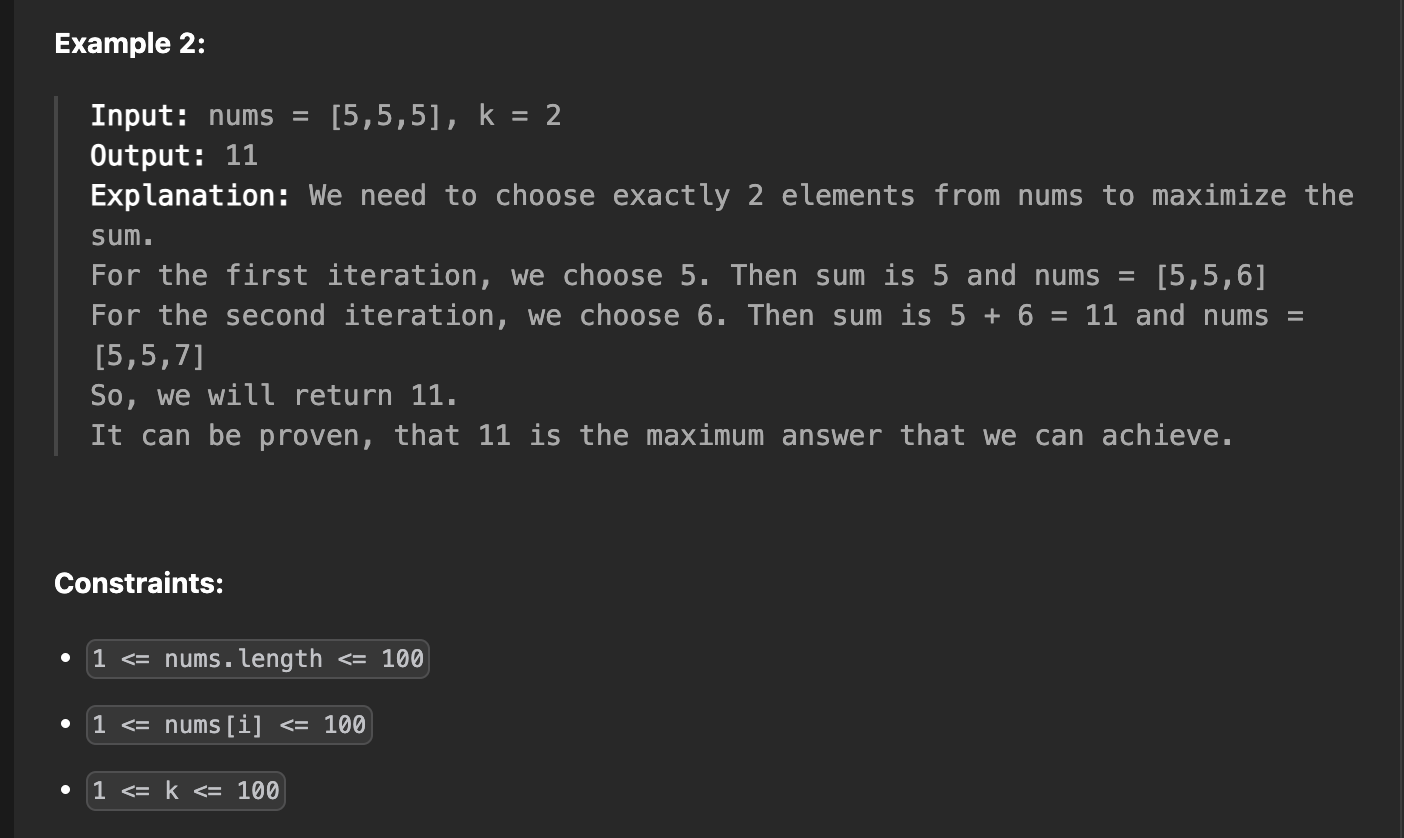
🎯 Strategy

Two approaches

As always, I tried two different ways to solve this problem. The first approach is the arithmetic approach, and the second approach is the stack approach.

Arithmatic apporach

Once we see the example carefully, we can derive a mathematical expression.

# Pseudocode
'''
summing the arithmatic series, S(n)
S(n) = n / 2 * { 2a + (n - 1)d }
where n is number of terms to add,
a is the first term
d is the common difference between terms
Hence,
'''
result = (k / 2) * (2 * maxNum + (k-1)*1)

If we choose to use the sum of the arithmetic series formula, we must consider the decimal point.

 def maximizeSum(self, nums: List[int], k: int) -> int:
 	return trunc((k/2) * (2 * max(nums) + (k-1)))

The time complexity is O(1), and the space complexity is O(1).

Stack approach

I solved this problem using the stack approach, which I practiced a lot when attending the Goormthon challenge.

First, we define a maxNum from the list and will iterate k times since k is the operation number.

Now, we will define stack as the empty list and append the current maxNum. After appending the current maxNum, we will add one to maxNum

Make a variable result, and while stack exists, add current to the result(which is the current maxNum).

This for-loop will iterate three times and break. After the iteration, we will return the result.

 def maximizeSum(self, nums: List[int], k: int) -> int:
 	maxNum = max(nums)
    result = 0
    
    for _ in range(k):
    	stack = []
    	stack.append(maxNum)
        maxNum += 1
        
        while stack:
        	current = stack.pop()
            result += current
            
    return result

The time complexity is O(n), and the space complexity is O(1).

📌 Thoughts

I tried to use the stack method since I practiced a lot, but there was a more clever way to do this. I didn't know the sum of the arithmetic series formula, but I tried to learn the formula by Google search.

I'm not sure if I need to keep solving easy problems or move to medium problems. I will try to solve the first five problems, and if it is too easy, I will go to the next difficulty level.

💻 Solution

Arithmetic approach

def maximizeSum(self, nums: List[int], k: int) -> int:
	return trunc((k/2) + (2 * max(nums) + (k-1)))

Stack Method

def maximizeSum(self, nums: List[int], k: int) -> int:
	maxNum = max(nums)
    result = 0
    
    for _ in range(k):
    	stack = []
        stack.append(maxNum)
        maxNum += 1
        
        while stack:
        	current = stack.pop()
            result += current
	return result