1051. Height Checker

Problem type - Array

🧩 Problem

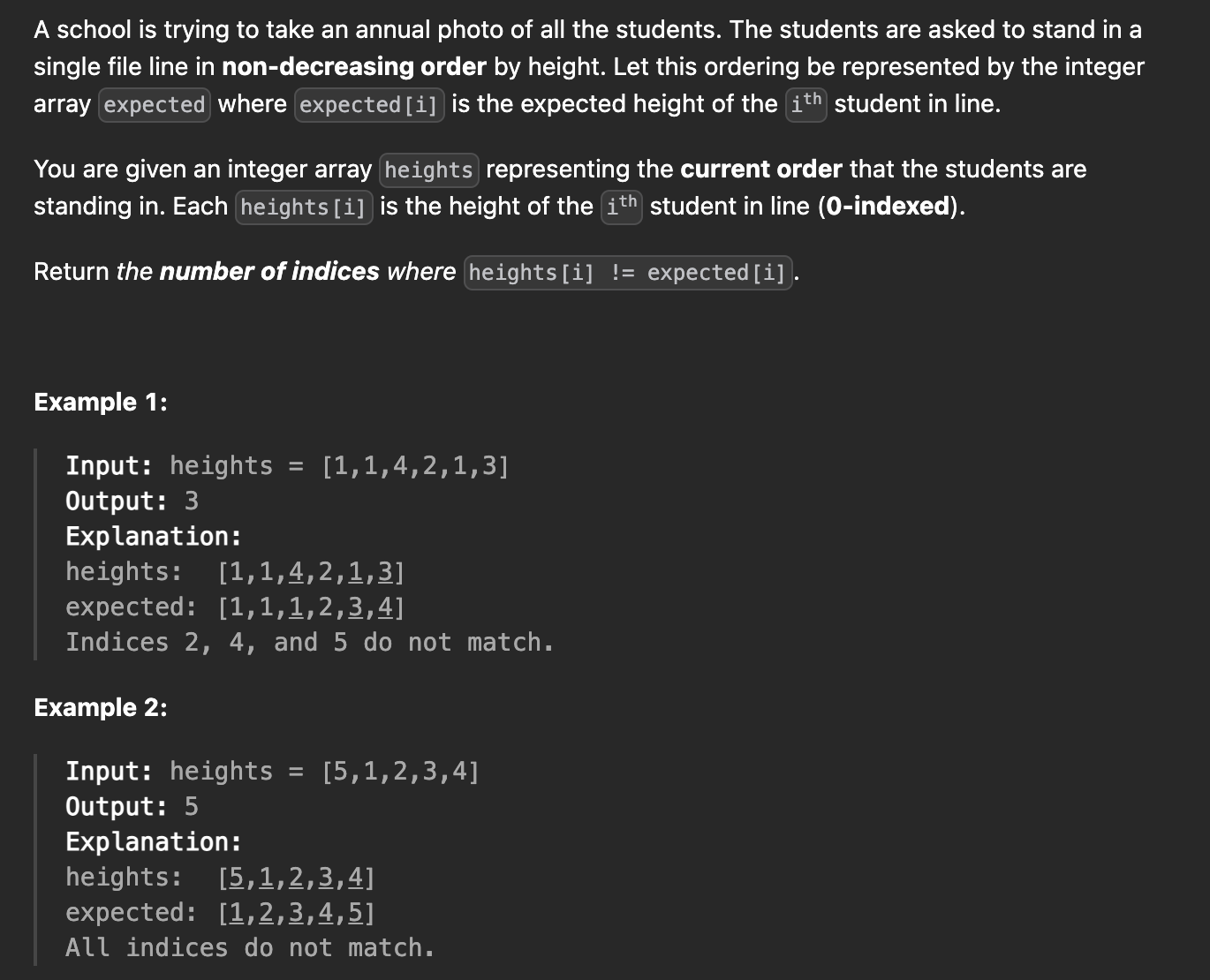
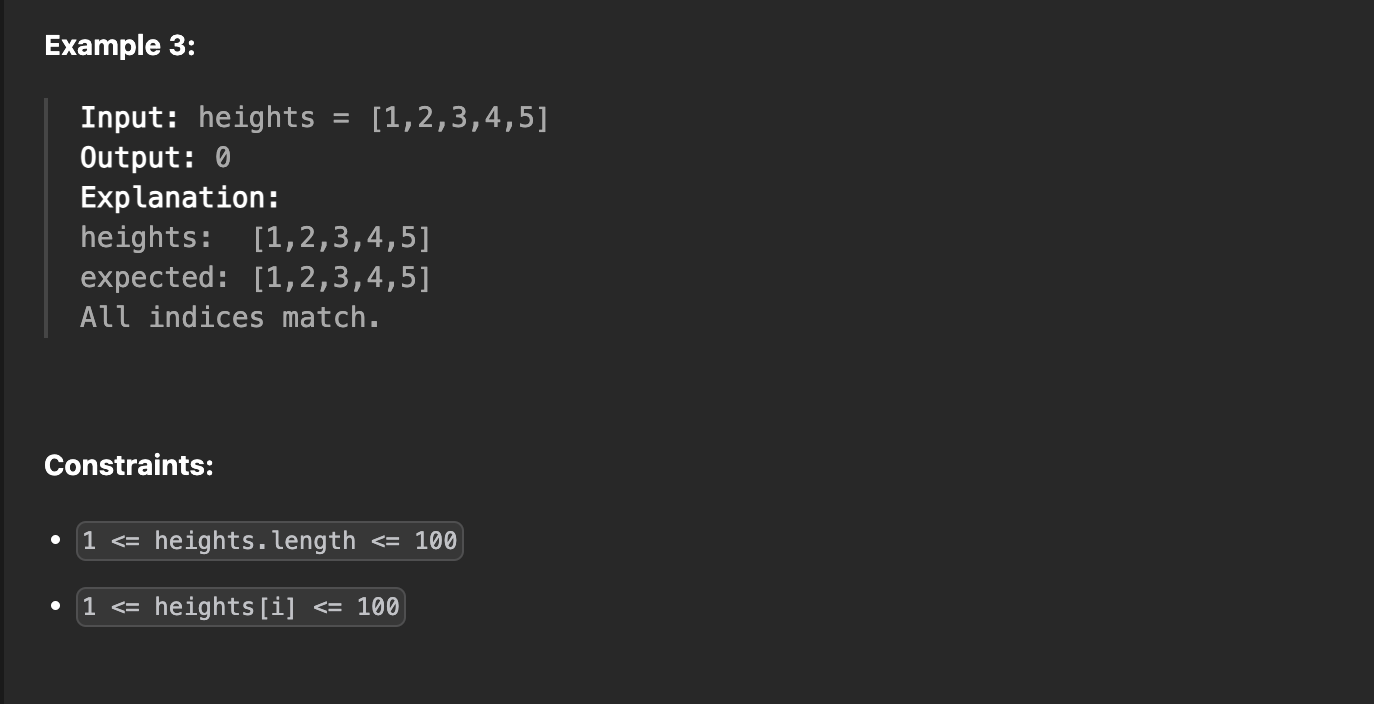
🎯 Strategy

The problem concept

A simple way to solve this problem is by comparing two arrays. We will compare the original and expected array, in which the expected array is sorted.

Then, we will return a count of the numbers that don't have the same value.

Regular approach

sorted() approach

We can sort the original array and assign it to a new variable, sort_h.

Set a counter to count if the original and sorted array sort_h items don't have the same value.

def heightChecker(self, heights: List[int]) -> int:
        counter = 0
        sort_h = sorted(heights)
        
        ...

Then, loop through the array until i reaches the end. We will do the logic that is explained above.

def heightChecker(self, heights: List[int]) -> int:
        counter = 0
        sort_h = sorted(heights)
        
        for i in range(len(heights)):
        	if heights[i] != sort_h[i]:
            	counter += 1
                
        ...

Finally, we will return a counter, which is the number of numbers that do not match.

def heightChecker(self, heights: List[int]) -> int:
        counter = 0
        sort_h = sorted(heights)
        
        for i in range(len(heights)):
        	if heights[i] != sort_h[i]:
            	counter += 1
                
        return counter

The time complexity is O(nlogn) because the dominant factor in the time complexity is the sorting operation, and sorted() typically has a time complexity of O(nlogn). The loop has a linear time complexity, but it doesn't dominate overall time complexity.

The space complexity is O(n), which means the sorted array sort_h requires extra space to store a new array.

advanced approach

Two-liner approach

This time, we will condense the above code into two lines of code.

The process assigning to a variable sort_h is the same.

def heightChecker(self, heights: List[int]) -> int:
        sort_h = sorted(heights)
        return sum([0 if heights[i] == sort_h[i] else 1 for i in range(len(heights))])

Notice we return a sum value of the array, while if two numbers are the same, the array is 0; otherwise, the array should be 1.

Then, we return the sum of 1s in the array.

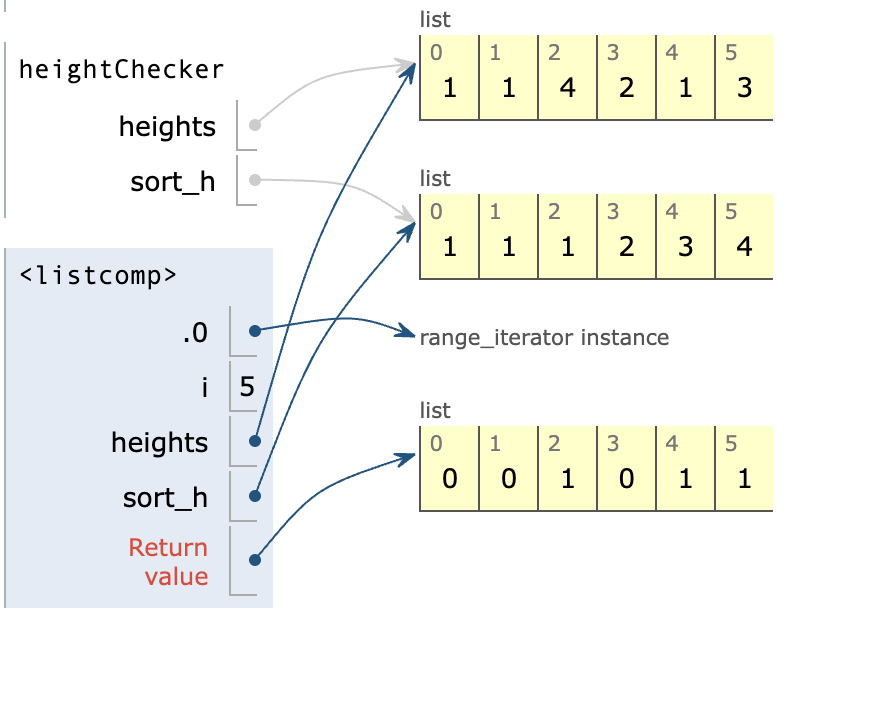
The time complexity is O(nlogn) because we just condensed. Hence, the logic is the same.

The space complexity is O(n), which has the same space complexity as above.

📌 Thoughts

The first counter logic was quite simple, and I just had to bring some sorted() logic from the memory.

I checked more solutions but brought this two-liner approach because it's intuitive and easy to understand.

💻 Solution

Regular approach

def heightChecker(self, heights: List[int]) -> int:
        counter = 0
        sort_h = sorted(heights)
        
        for i in range(len(heights)):
        	if heights[i] != sort_h[i]:
            	counter += 1
                
        return counter

Two-liner approach

def heightChecker(self, heights: List[int]) -> int:
        sort_h = sorted(heights)
        return sum([0 if heights[i] == sort_h[i] else 1 for i in range(len(heights))])

🔖 Review

Problem type - Array(in-place)

This is a review problem, so there is no strategy part. But there will be two approaches: the in-place approach and the one-liner approach.

🧩 Problem

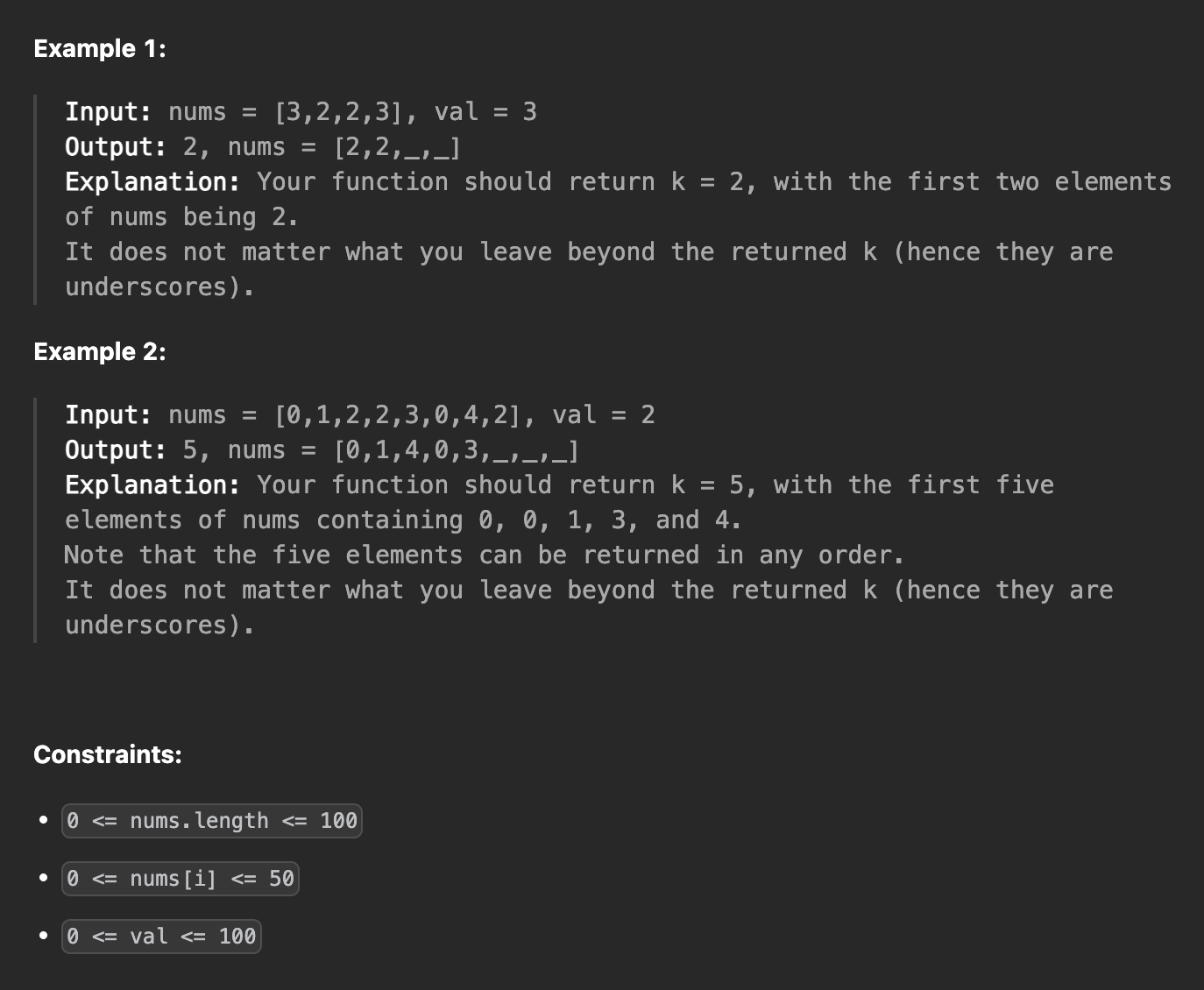
💻 Solution

Two-pointer approach

def removeElement(self, nums: List[int], val: int) -> int:
        k = 0
        
        for num in nums:
        	if num != val:
            	nums[k] = num
            	k += 1
                
        return k

One-liner approach

def removeElement(self, nums: List[int], val: int) -> int:
        nums[:] = [i for i in nums if i != val]

The time complexity is O(n) because the function iterates through the array only once.

The space complexity is O(1) because the list comprehension creates a new list, but it does not depend on the size of the input array.

📌 Thoughts

When I solved this question for the first time, I couldn't solve the problem easily. After solving a few similar types of questions, it took less time, which made me feel accomplished.