941. Valid Mountain Array

Problem type - Array

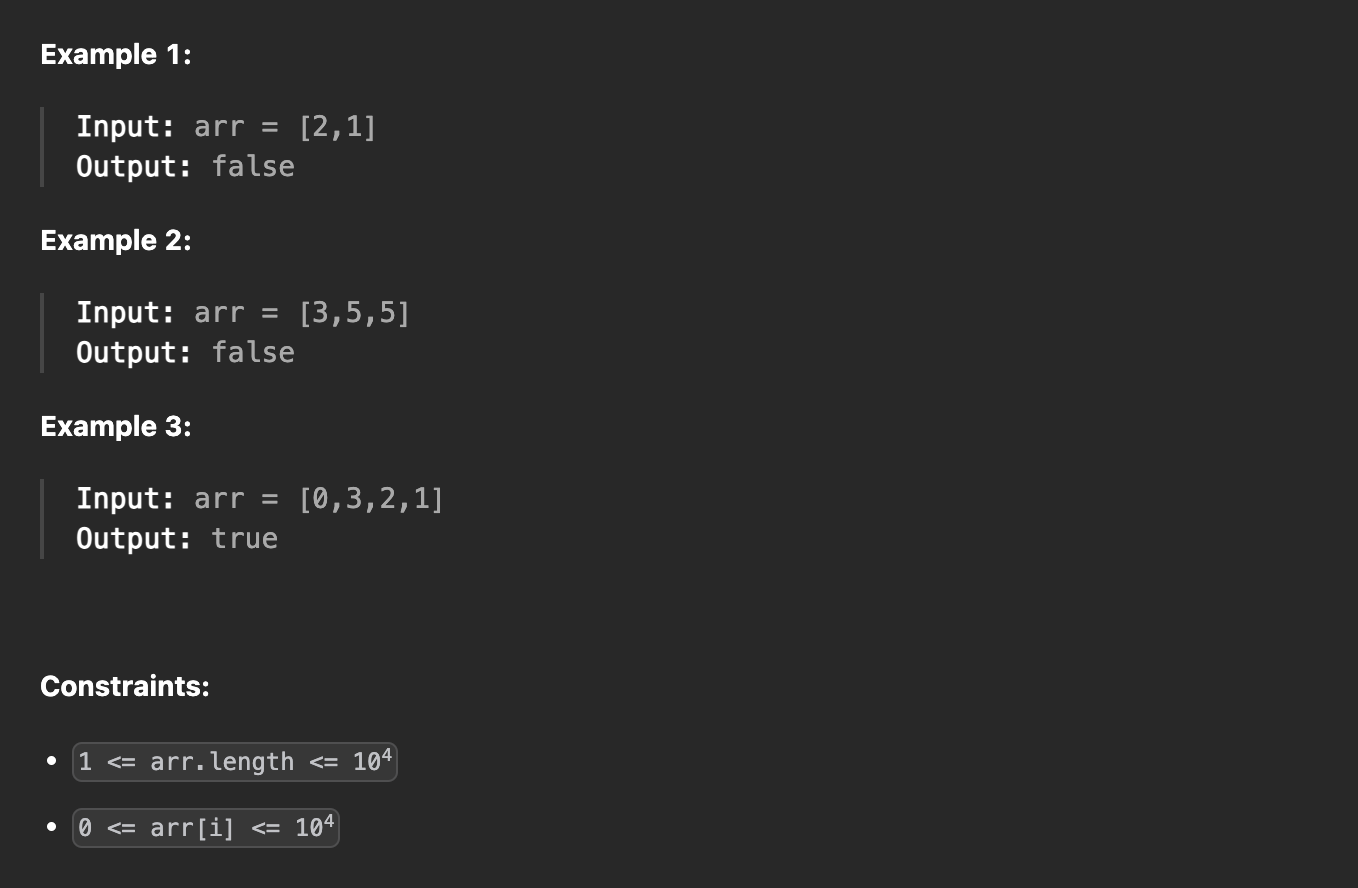
🧩 Problem

🎯 Strategy

Understand the concept

This problem is a well-known problem for people who are studying algorithms.

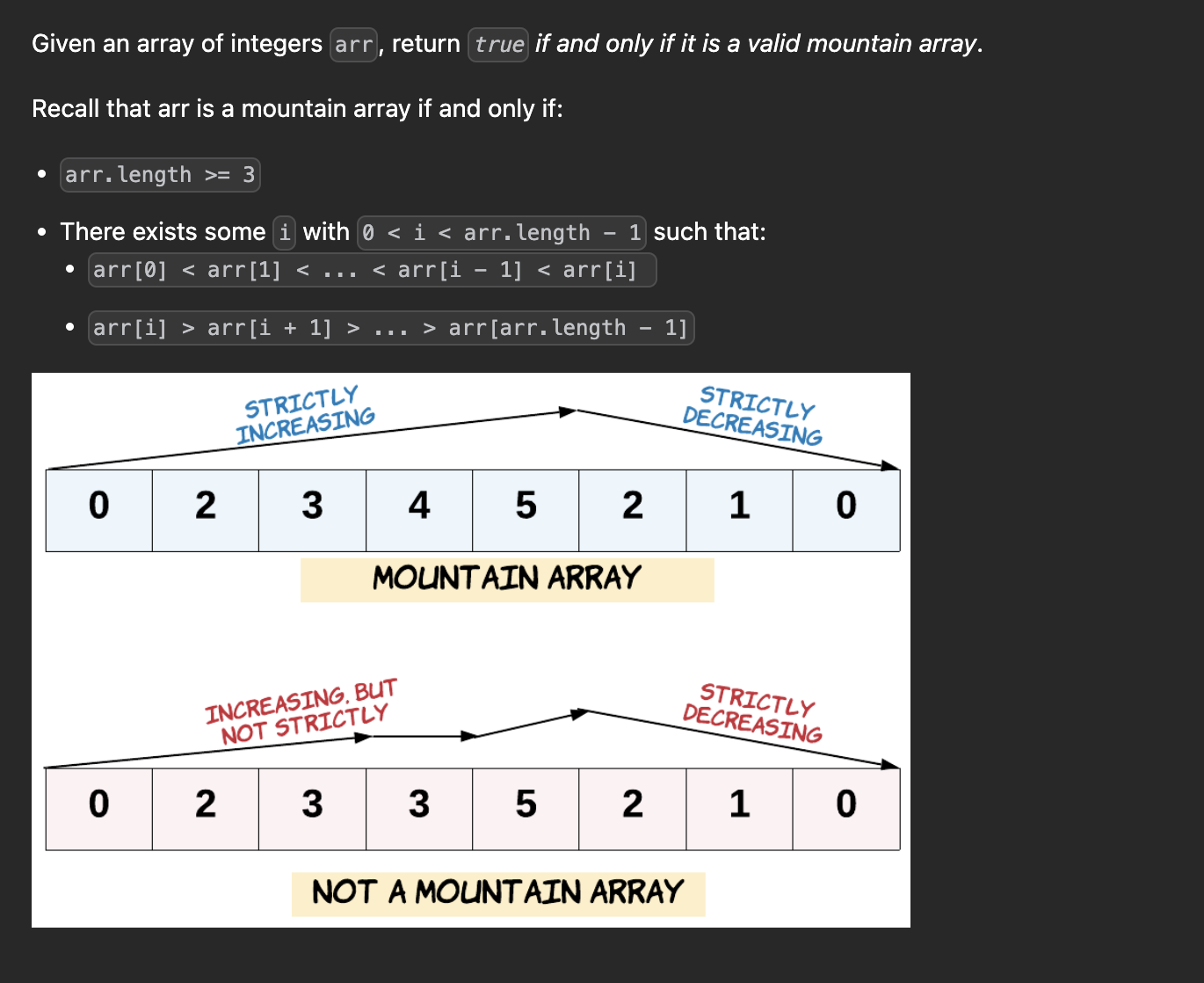
Like the mountain, the numbers in the array should be uphill and downhill. But the hills have to be strictly increasing and strictly decreasing.

Loop approach

for loop approach

We set the initial state as True and use the for loop to iterate the arr.

def validMountainArray(self, arr: List[int]) -> bool:
	state = True
    for i in range(len(arr)-1):
    	# logic

Then check if the state is True and the current number arr[i] is bigger than the next number arr[i+1]. We should change the logic if the next number, arr[i+1], becomes bigger. Hence, we will set the state to False at that point.

def validMountainArray(self, arr: List[int]) -> bool:
	state = True
    for i in range(len(arr)-1):
    	if state and arr[i] >= arr[i+1]:
        	state = False
        # change

If the state changed to False, we check whether the current number arr[i] is less than the next number arr[i+1]. If arr[i] <= arr[i+1], it means the array is not strictly decreasing. Hence, we should return False.

If the loop ends, it means none of the conditions matched. We can return True. Also, we have to add an edge case checker to return False before entering the loop.

The edge cases are simple if the max number in the array shouldn't be in first or last place and the array's length should be longer than two.

Essentially, the loop works as a filter in this approach. If any condition matches, that array is not the mountain array.

def validMountainArray(self, arr: List[int]) -> bool:
	if len(arr) == 2 or max(arr) == arr[0] or max(arr) == arr[len(arr)-1]:
    	return False
    
	state = True
    for i in range(len(arr)-1):
    	if state and arr[i] >= arr[i+1]:
        	state = False
        if not state and arr[i] <= arr[i+1]:
        	return False
            
     return True

The time complexity is O(n) because the function iterates through the array only once.

The space complexity is O(1), as the code uses a constant amount of extra space regardless of the input size. The variables state and i are integers, and the function does not use any additional data structure.

Two-pointer approach

While loop approach

Another approach that we can use is the two-pointer approach. We set the two pointers s and e as the start and end points from the array. Additionally, we will set the l to track the length of the array.

def validMountainArray(self, arr: List[int]) -> bool:
	l = len(arr)
    s = 0
    e = l - 1
    ...

Then, use the while loop to check from the first element of the array. If the array increases, we will add one to s each time we check.

def validMountainArray(self, arr: List[int]) -> bool:
	l = len(arr)
    s = 0
    e = l - 1
    
    while s < e and arr[s] < arr[s+1]:
    	s += 1
        
    ...

Similarly, we use the while loop, but this time, we will check if the array is increasing from the last element of the array.

def validMountainArray(self, arr: List[int]) -> bool:
	l = len(arr)
    s = 0
    e = l - 1
    
    while s < e and arr[s] < arr[s+1]:
    	s += 1
        
    while e > 0 and arr[e] < arr[e-1]:
    	e -= 1
        
    ...

Lastly, we have to check the conditions using s and e to return True or False.

We will return True because if s==e, the array is a complete mountain. But we need to add the edge cases: the e and the last element shouldn't be the same. The s shouldn't be at the initial point.

def validMountainArray(self, arr: List[int]) -> bool:
	l = len(arr)
    s = 0
    e = l - 1
    
    while s < e and arr[s] < arr[s+1]:
    	s += 1
        
    while e > 0 and arr[e] < arr[e-1]:
    	e -= 1
        
    return True if s == e and e != l-1 and s!=0 else False

The time complexity is O(n) because two while loops have O(n) time separately, making the overall complexity linear with the input size.

The space complexity is O(n) since the variables l, s, and e are all integers and don't depend on the size of the input array.

📌 Thoughts

I thought the while loop had less time complexity because of the max(), but it turns out they have almost the same time complexity.

The while loop approach was quite new to me, so I need to practice and face more problems to apply this new approach.

💻 Solution

For loop approach

def validMountainArray(self, arr: List[int]) -> bool:
	if len(arr) <= 2 or max(arr) == arr[0] or max(arr) == arr[len(arr)-1]:
    	return False
    
    state = True
    
    for i in range(len(arr)-1):
    	if state and arr[i] >= arr[i+1]:
        	state = False
        if not state and arr[i] <= arr[i+1]:
        	return False
            
    return True

Two-pointer/while loop approach

def validMountainArray(self, arr: List[int]) -> bool:
	l = len(arr)
    s = 0
    e = l - 1
    
    while s < e and arr[s] < arr[s+1]:
    	s += 1
    while e > 0 and arr[e] < arr[e-1]:
    	e -= 1
        
    return True if s==e and e!=l-1 and s!=0 else False