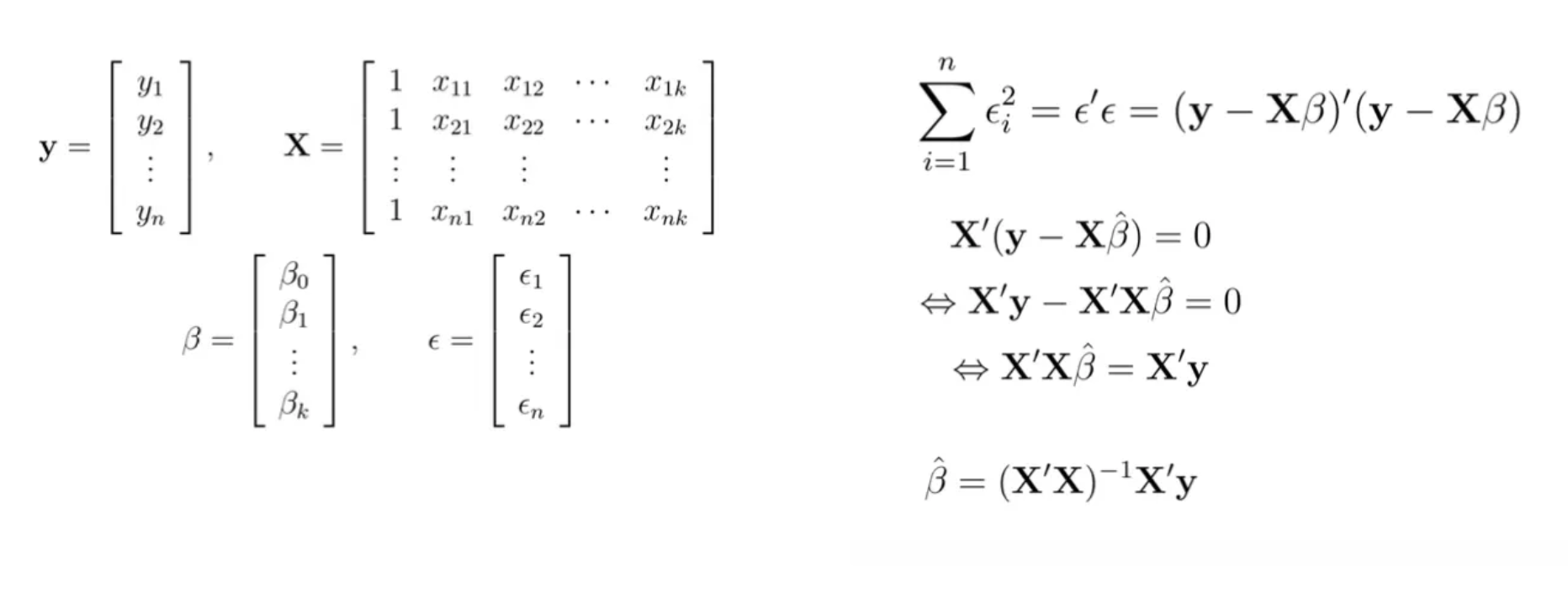Linear Regression

Linear Regression이란?

• 종속 변수(Dependent Variable)와 하나 이상의 독립 변수(Independent Variable) 간의 관계를 선형적인 함수(직선)로 모델링하는 기법이다.

Deterministic Models

• 무작위성이 없다고 가정한다.
• 변수간의 정확한 관계가 있다.
• ex) BMI(체질량지수)

Probabilistic Models

• 현실 세계의 불확실성을 모델에 포함시킨 것이다.
• 두 가지 요소로 구성된다.
  • 결정론적 요소: 변수에 의해 정확하게 결정되는 규칙적인 부분
  • 무작위 오차: 변수만으로는 설명되지 않는 불확실한 부분
• ex) 신생아의 수축기 혈압(SBP)
  SBP = 6 age(days) + $\epsilon$
  → 6age(days)는 결정론적 요소
  → 입실론은 무작위 오차

Regression Models

• 데이터사이언스에서 말하는 Regression Models은 Probabilistic Models을 의미하는 것이다.
• Regression Model은 dependent variable(종속변수)와 explanatory variable(설명변수) 간의 관계를 설명하는 것이다.
• Prediction(예측)과 Estimation(추정)이 주된 목적이다.

Specifying the Deterministic Component

• 모델에서 수식으로 설명할 수 있는 규칙 부분을 어떻게 설정할지 정하는 과정은 크게 두 가지 단계로 나눌 수 있다.
  • 변수 정의: 무엇을 예측할지, 무엇을 가지고 예측할지 정하는 것
  • 가설 수립: 수학적으로 어떤 모양일지 가설을 수립하는 것
    → 함수 형태 Linear or Non-Linear

Types of Regression Models

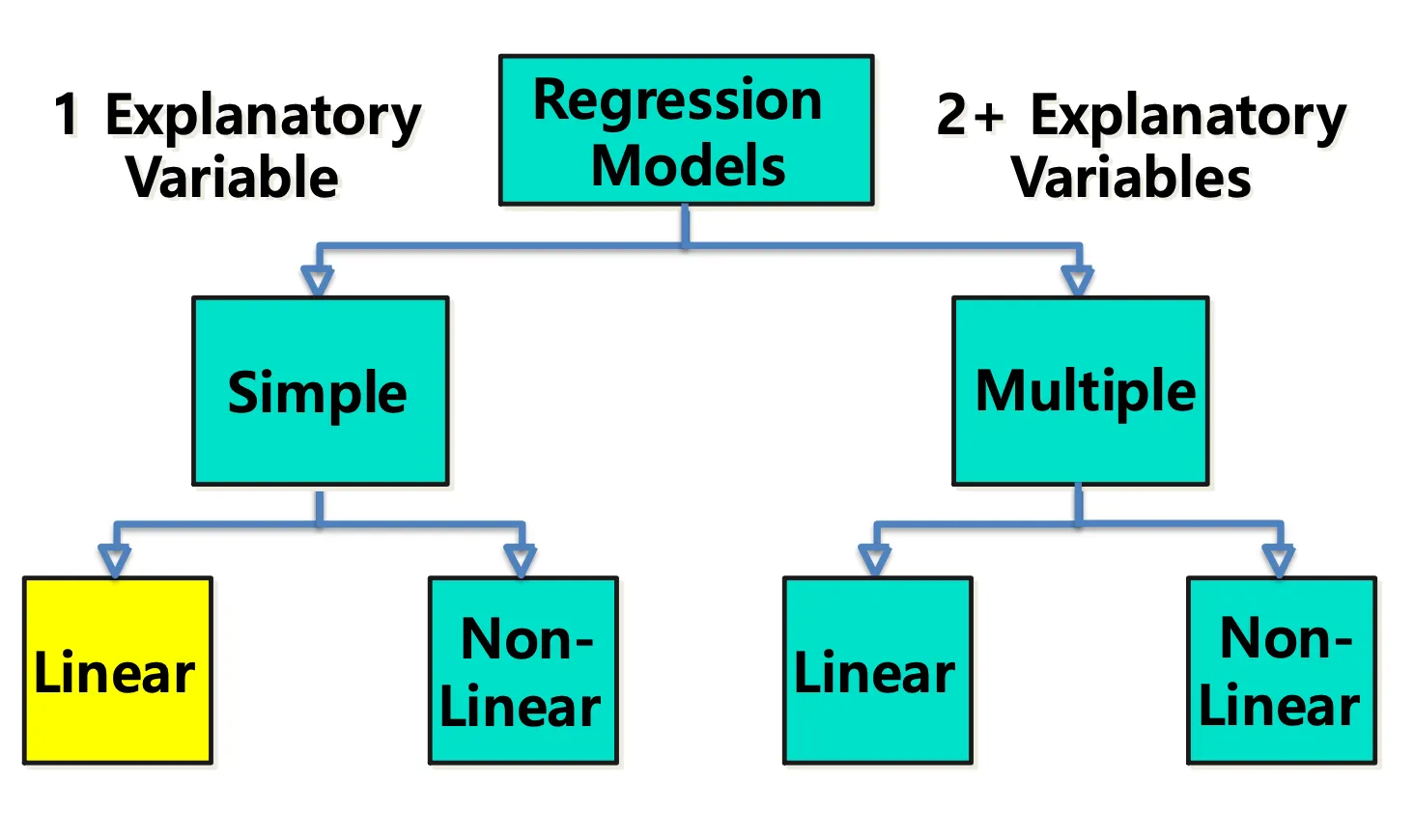
Linear Equations

Population vs Sample Regression

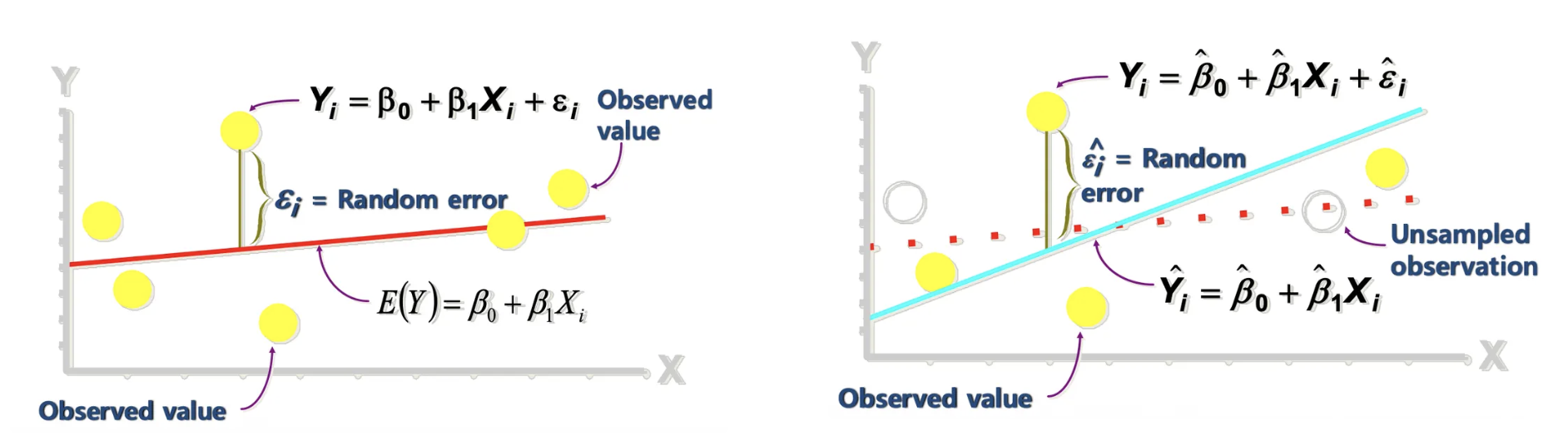
• Population Regression (모집단 회귀): 모집단은 전체 데이터 집합을 의미한다. 현실적으로 전체를 다 조사하는 것은 불가능하므로 관측이 불가능하다. (Not Observable)
• Sample Regression (표본 회귀): 실제로 수집한 일부 데이터(표본)을 가지고 계산한 회귀선이다. 회귀선을 통해 관측 가능하다.(Observable)
• 표본(Sample)이 충분히 크고, 무작위로 선택(Randomly Selected)되었다면 Sample Regression Line은 Population Regression Line의 좋은 근사치가 될 수 있다.
• Hyperthesis test(통계적 가설 검정): 표본의 정보를 사용해서 가설의 합당성 여부를 판정하는 과정
• Sample 데이터에 대한 regression을 수행하고, 이에 대한 Hyperthesis test를 통해서, 결과에 대한 합당성을 판정한다.

Estimating Parameters: Least Squares Method

Least Squares

• 실제값과 예측값의 차이를 통해 가장 좋은 직선을 찾아 나간다.
• SSE (Sum of Squared Errors): $S = \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2 = \sum_{i=1}^{n} (Y_i - (\beta_0 + \beta_1 X_i))^2$
  
• 왜 제곱을 하는가? → 오차를 단순히 더하면 양수와 음수가 서로 상쇄되어 0이 될 수 있다. → 따라서 부호를 없애고 오차의 크기 자체를 줄이기 위해 오차를 제곱해서 더한다.

Estimating $\beta_0, \beta_1$

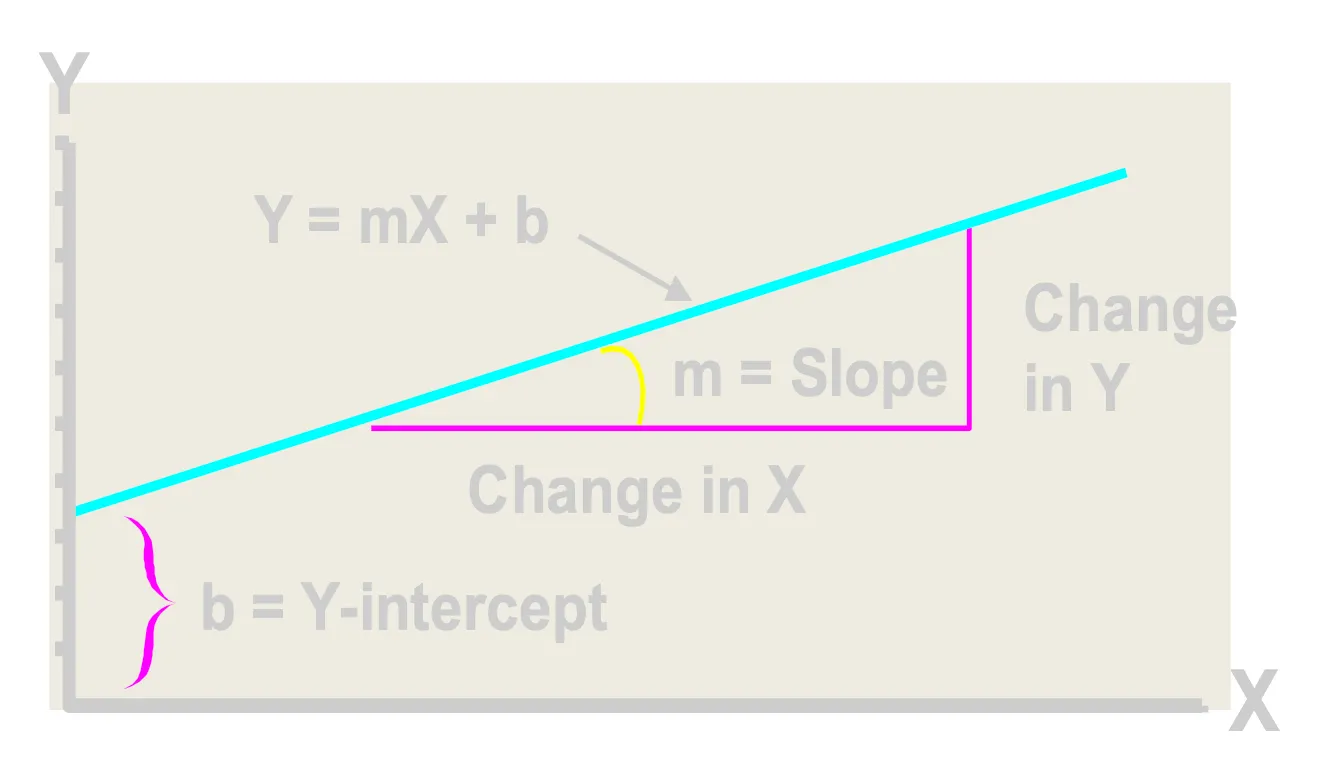
Interpretation of Coefficients (계수 해석)

• Slope(기울기, $\beta_1$)
  • X가 변할 때 Y가 얼마나 민감하게 반응하는가를 나타낸다.
  • 독립변수(X)가 1단위 증가할 때, 종속변수(Y)는 $\beta_1$만큼 변한다고(증가 또는 감소) 추정한다.
• Y-Intercept(Y-절편, $\beta_0$)
  • 그래프가 Y축과 만나는 점으로, 시작점이나 기본값을 의미한다.
  • 독립변수(X)가 0일 때, 종속변수(Y)의 평균적인 값이다.

Goodness of Fit for Simple Linear Regression

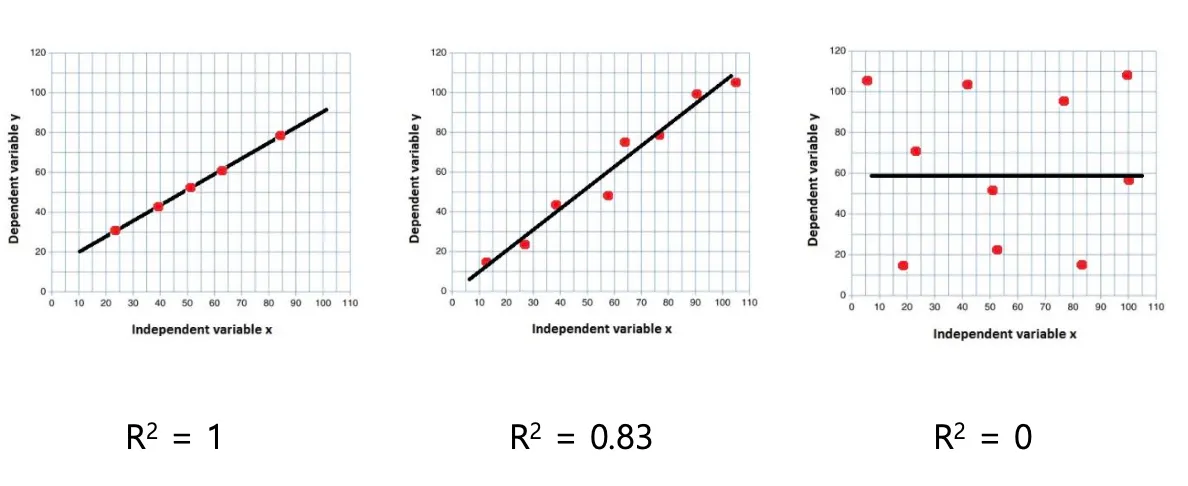
$R^2$ (R-squared, 결정계수)

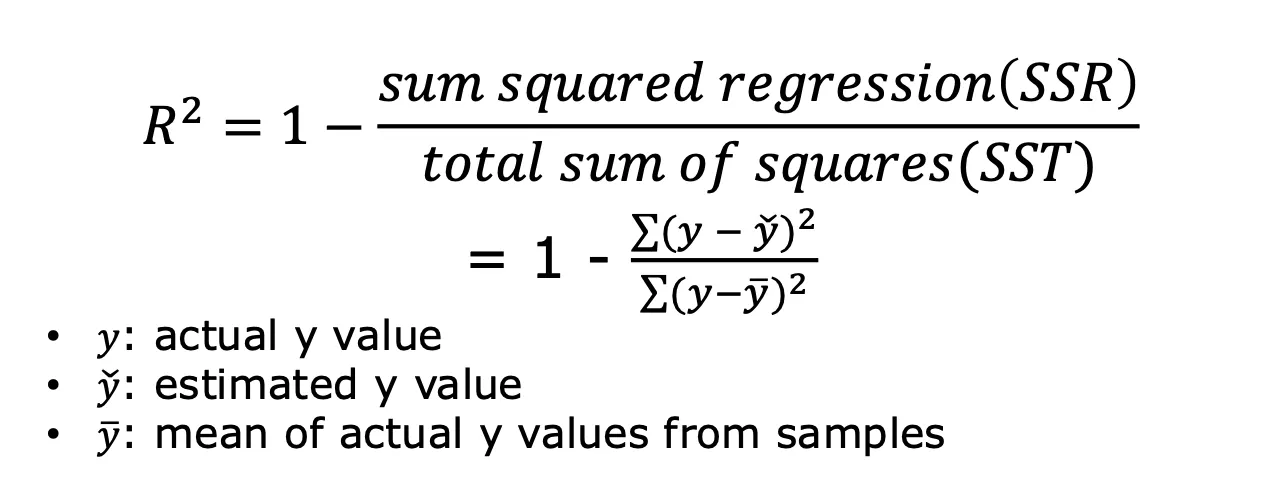
• 회귀모델이 실제 데이터를 얼마나 잘 설명하고 있는가를 0과 1사이의 숫자로 나타낸 지표이다.
• 의미: regression line이 얼마나 실제 데이터를 가깝게 설명하는지를 나타내는 수치이다.
• 해당값 만큼 y 값의 variation이 regression line으로 잘 설명된다는 의미이다.

SE (Standard Error of Estimate)

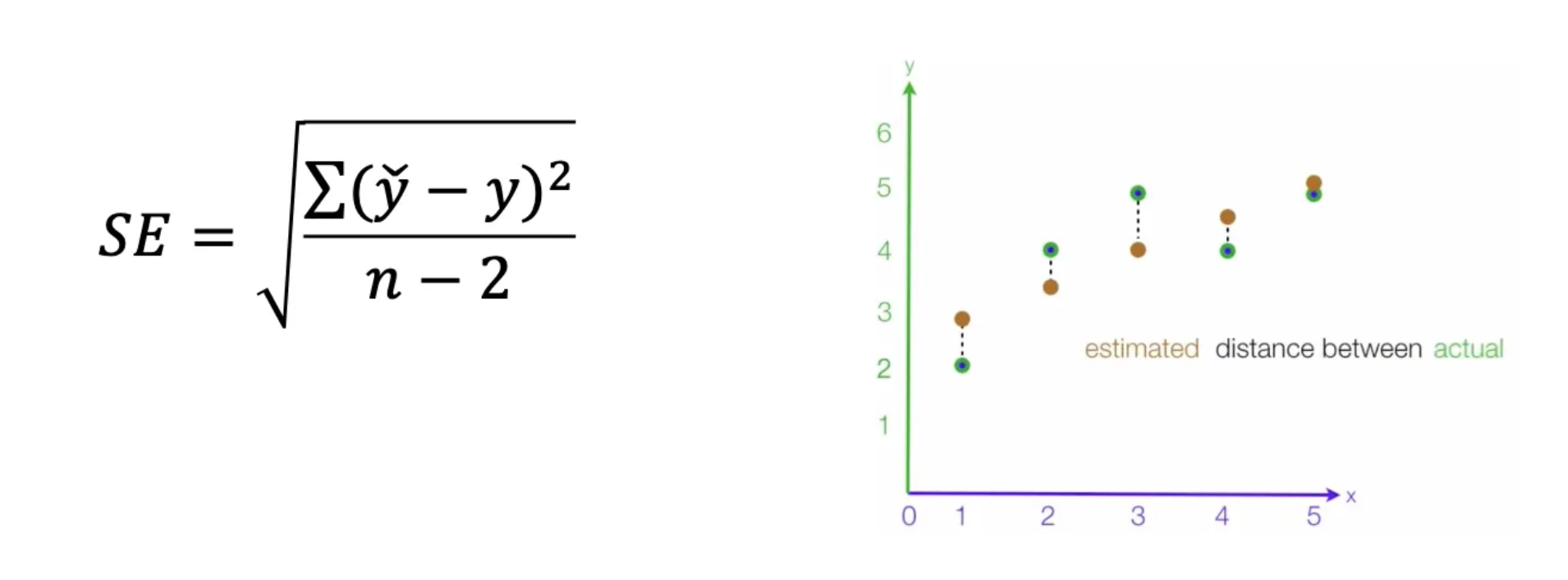
• 회귀모델이 실제 데이터와 평균적으로 얼마나 떨어져 있는지를 나타내는 지표이다. 즉, 모델의 예측이 얼마나 정밀한지를 보여주는 값이다.
• DF(degree of freedom, 자유도) = n-2
  • 오차를 계산하기 위해 2개의 파라미터(기울기, 절편)를 미리 추정해서 사용했기 때문에 n-2를 사용한다.
• SE 값은 작을수록 좋다.

통계학에서 말하는 degree of freedom

• 어떤 통계치를 계산하기 위해 미리 구해놓은(고정된) 다른 추정치가 있다면, 그 개수만큼 전체 데이터 개수(n)에서 뺀다.
• ex)
  • df(표본평균) = n
  • df(표준편차) = n-1 ← 표준편차를 계산하려면 먼저 표본평균을 알아야하기 때문
  • df(SE) = n-(k+1) ← k개의 slope와 1개의 intercept 추정치가 입력으로 사용되기 때문

SE of coefficients

• 각 coefficient에 대한 표준에러
• 예측한 coefficient의 정확도가 얼마나 되는지를 나타냄
• 이것도 구할 수 있다 정도로 알고 넘어가면 된다라고 하심

linear regression 결과 검증

이 모델이 정말 믿을만한지, 그리고 변수들 간의 관계가 우연이 아니라 진짜 통계적으로 의미가 있는지를 깐깐하게 따져보는 단계이다.

• 관계가 어느 정도인가?
  • R-squared
  • SE(Standard Error)
• 통계적으로 유의미한가?
  • t-test
  • Confidence Interval(신뢰도 구간)

T-test

구한 기울기가 통계적으로 정말 의미가 있는 값인가?를 검증하는 절차이다.

• 가설 설정 (Hypothesis Setup)
  • 두 가지 상반된 가설을 세우고 시작한다.
  • 귀무가설 ($H_0$, Null Hypothesis): 아무런 관계가 없다.
    • 수식: $\beta_1 = 0$
    • 의미: 기울기가 0이므로, X가 변해도 Y는 변하지 않는다.
  • 대립가설 ($H_a$, Alternative Hypothesis): 관계가 있다.
    • 수식: $\beta_1 \neq 0$
    • 의미: 기울기가 0이 아니므로, X가 변하면 Y도 변한다.
• t-value 계산
  • 우리가 구한 기울기($\hat{\beta}_1$)가 0에서 얼마나 멀리 떨어져 있는지를 표준 오차(SE) 단위로 잰 값이다.
  • 이 t값(절대값)이 클수록 0에서 멀리 떨어져 있다는 뜻이므로, 관계가 있다($H_a$)는 주장에 힘이 실린다.
  • 반대로 t값이 0에 가깝다면, 기울기가 사실상 0이나 다름없다는 뜻이 된다.
• P-value와 유의수준($\alpha$)
  • 계산한 t-value를 가지고 최종 판결을 내린다.
  • P-value (유의확률): 만약 진짜로 관계가 없는데($\beta_1=0$), 우연히 내 데이터처럼 기울기가 나올 확률이다.
    • 이 확률이 아주 낮아야 우연이 아님을 확신할 수 있다.
  • 유의수준 ($\alpha$, Significance Level): 허용할 수 있는 오차의 한계이다. 보통 0.05 (5%)를 많이 사용한다.
  • [판정규칙]
    • P-value < $\alpha$ (예: 0.05): 우연일 확률이 5%도 안 된다.
      • 결론: 귀무가설 기각 → 통계적으로 유의미한 관계가 있다.
    • P-value $\ge \alpha$: 우연히 이렇게 나올 수도 있다.
      • 결론: 귀무가설 기각 실패 → 관계가 있다고 단정 짓기 어렵다.

t-value and p-value

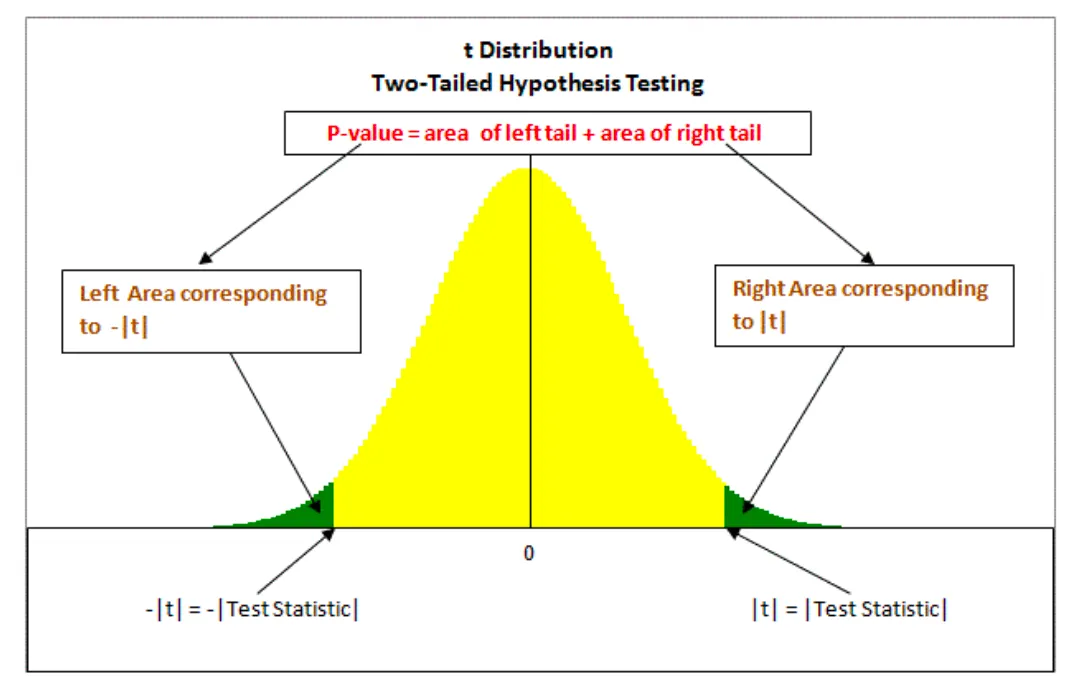
Multiple linear regression

단순 선형 회귀(Simple Linear Regression)가 하나의 설명 변수(X)로 종속 변수(Y)를 설명했다면, 다중 선형 회귀는 두 개 이상의 설명 변수가 함께 작용하여 Y를 설명하는 모델이다.

• 수식
  • $Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k + \epsilon$
• 파라미터 추정
  • 여기서도 최소 제곱법(Least Squares Method)을 사용하여 오차의 제곱합을 최소화하는 $\beta$들을 찾는다.
• ex

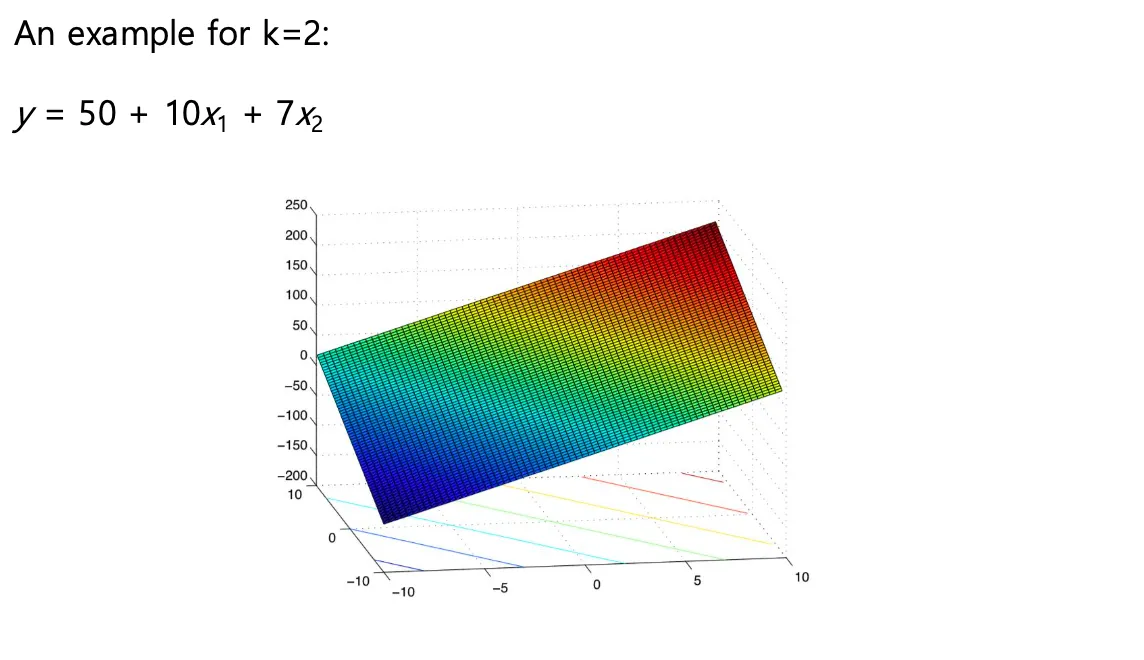
Linear algebra method