Measuring Complexity of Fibonacci Algorithms (Memoization & Big O)

Dynamic Programming

This exercise is an example of dynamic programming, which is defined as..

mainly an optimization over plain recursion. [...] The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.

For example, if we write simple recursive solution for Fibonacci Numbers, we get exponential time complexity and if we optimize it by storing solutions of subproblems, time complexity reduces to linear.

Big O Notation

Big O Notation is a way to measure an algorithm’s efficiency. It measures the time it takes to run your function as the input grows. Or in other words, how well does the function scale. ~Towards Data Science

The notation describes a complexity of a algorithm in algebraic terms, and also represents an algorithm's worst case complexity.

Time & Space Complexity

There are two essential parts to measuring the efficiency and performance of an algorithm: time complexity and space complexity. Time complexity represents how long the function takes to run in terms of its computation steps, and space complexity is related to the amount of memory used by the function.

Big O defines the runtime required to execute an algorithm by identifying how the performance of your algorithm will change as the input size grows. But it does not tell you how fast your algorithm's runtime is.

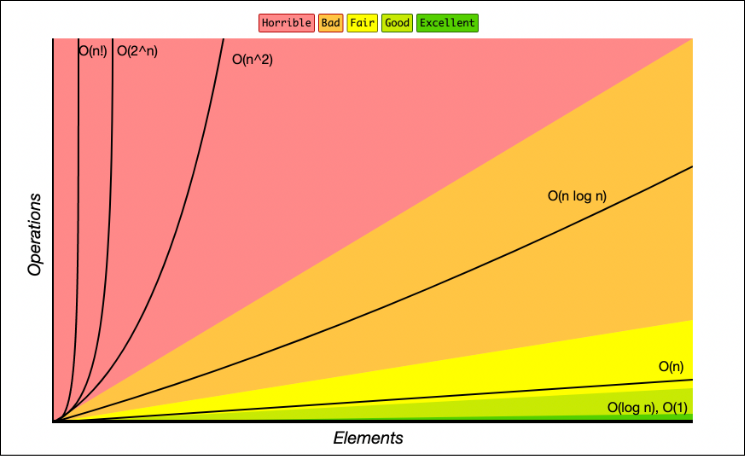
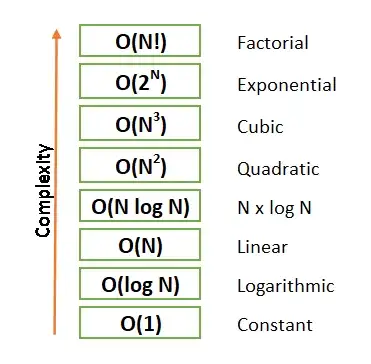
Types of Complexity

• Constant: O(1)
  (not dependent on input size. e.g. if an algorithm is to return the first element of an array)

• Linear time: O(n)
  (e.g. simple factorial function, linear search)

• Logarithmic time: O(n log n)
  (e.g. binary search)

• Quadratic time: O(n^2)
  (e.g. loop within a loop)

• Exponential time: O(2^n)
  (e.g. recursive fibonacci sequence)

• Factorial time: O(n!)

Binary Search:

function binarySearch(v,To_Find){
    let lo = 0;
    let hi = v.length - 1;
    let mid;
     
    // for mid=lo-(hi-lo)/2
    while (hi - lo > 1) {
        let mid = Math.floor((hi + lo) / 2);
        if (v[mid] < To_Find) lo = mid + 1;
        else hi = mid;
    }
    
    return v[lo] !== To_Find && v[hi] !== To_Find ? false : true; 
}

const isSubsetOf = function (base, sample) {
    base.sort((a,b) => a - b);
    return sample.every(el => binarySearch(base, el));
  };

Recursion is Computationally Expensive

Classic Fibonacci Algorithm

function fibonacci(num) {
  if (num <= 1) return num;
  return fibonacci(num - 1) + fibonacci(num - 2);
}

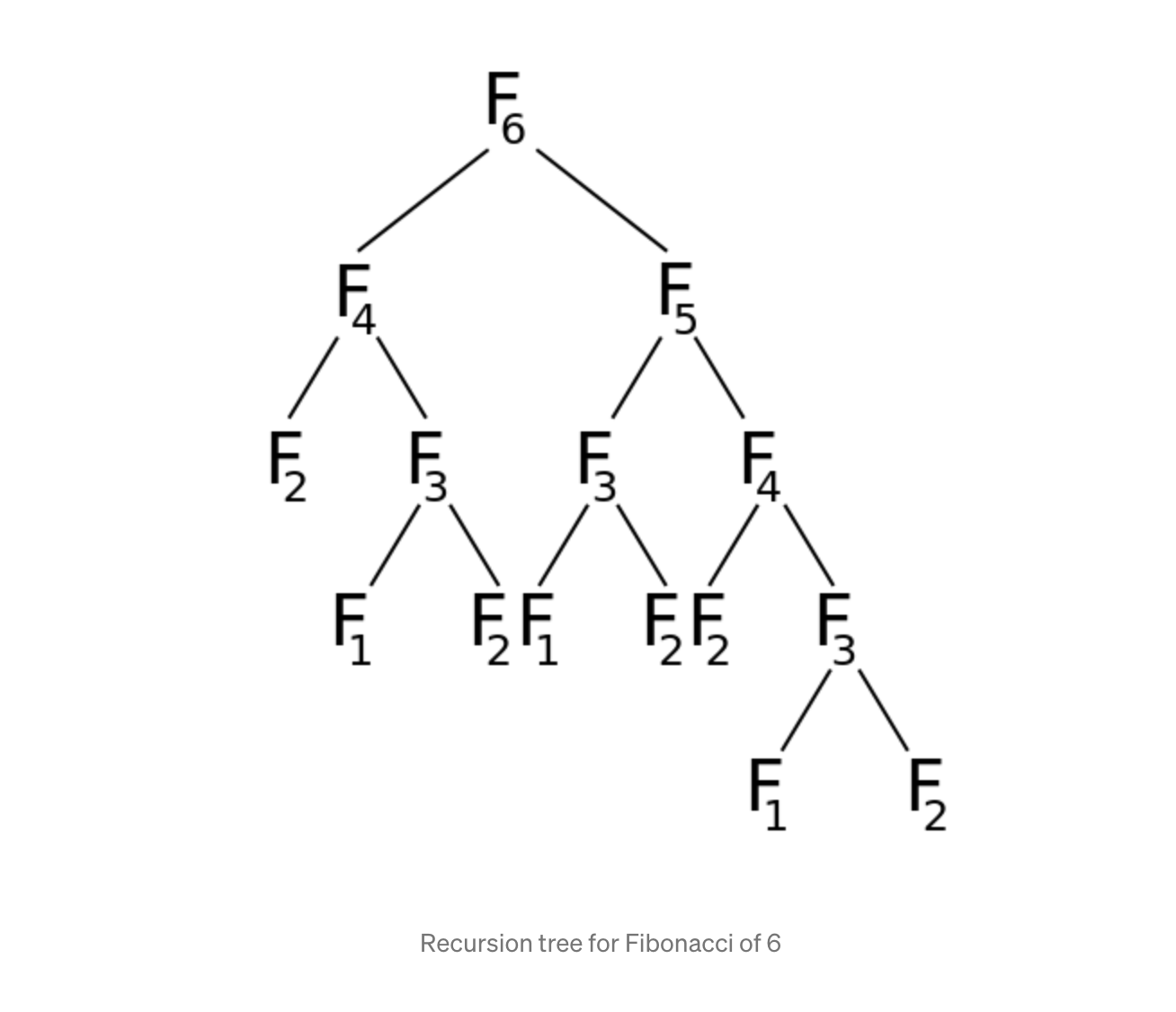
The classic algorithm specifies a growth rate that doubles every time the input data set is added, which means the time complexity is exponential with an order O(2^n).

T(n) = T(n-1) + T(n-2) + C
T(n) = O(2^(n-1)) + O(2^(n-2)) + O(1) since each recursive call creates a binary tree of calls

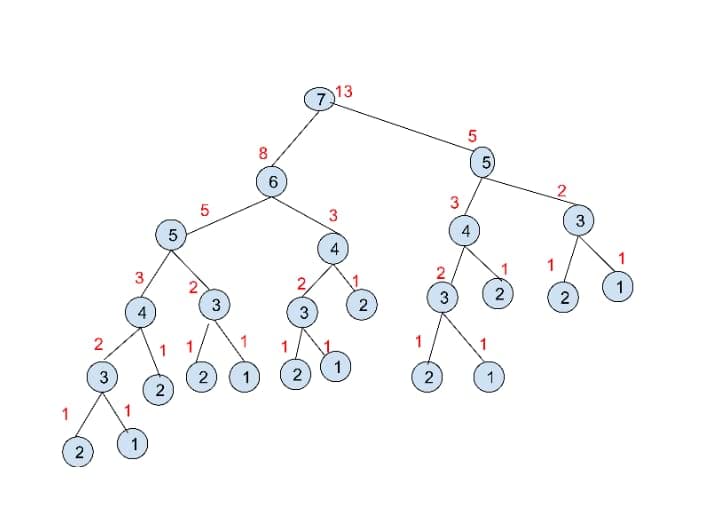
How fibonacci(7) would work:

Fibonacci with Memoization

 const memo = {};
 function fibonacci(n){
     if (n in memo) return memo[n];
     if (n <= 1) return n;
     else return memo[n] = fibonacci(n-1) + fibonacci(n-2);
}

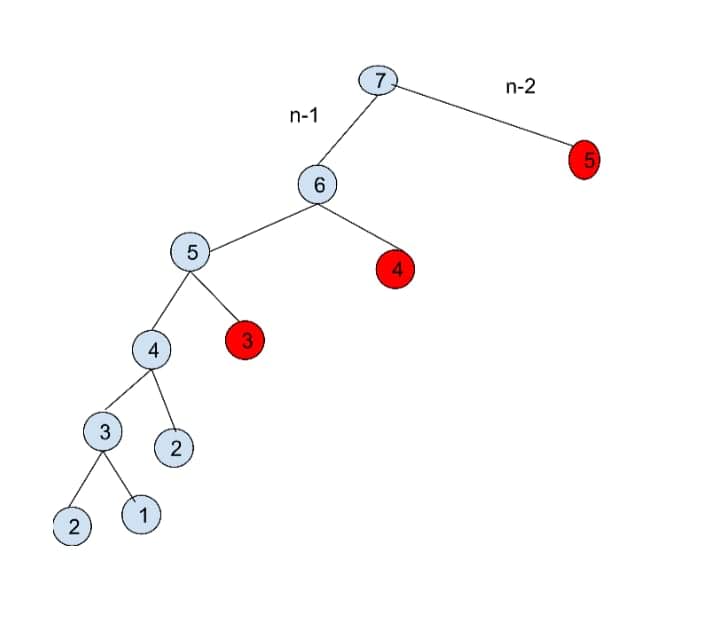
In the above image, the red nodes return the memoized result. The algorithm is called once for each value from 0 to n if ignored. Therefore this algorithm runs in O(n).

The space complexity is also equivalent to O(n)

Fibonacci with TCO

function fibonacci(n, current = 1, prev = 0) {
  if (n === 0) return prev; 
  return fibonacci(n - 1, current+prev, current); 
}

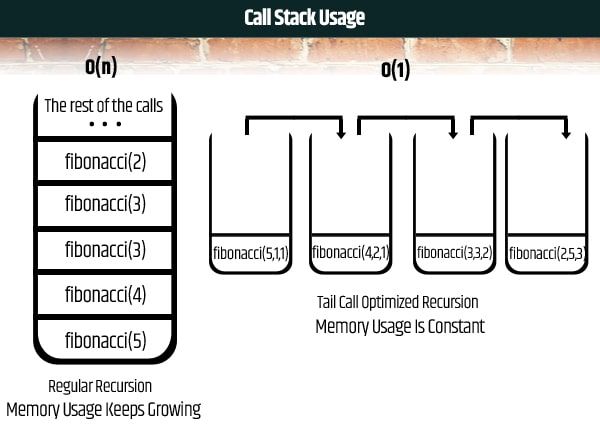
This inefficiency:

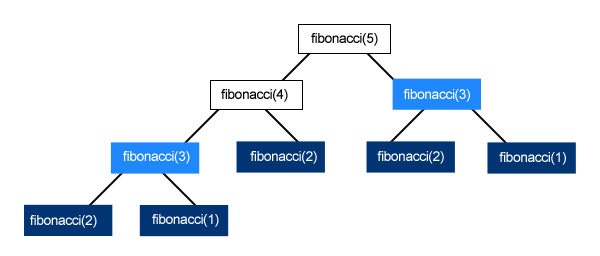
is transformed into this with TCO:

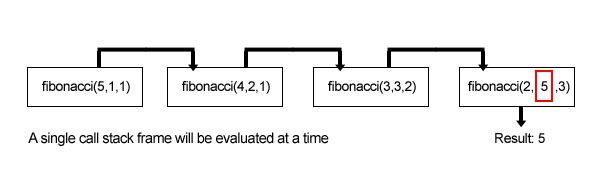
Measuring the performance with Big O:

References

• Dynamic Programming
• Using Fibonacci to Exemplify Recursion, Big O, and Memoization: Good overall explanation
• Understanding Fibonacci Memoization Time Complexity in JavaScript: Great visualization
• Fibonacci Iterative vs. Recursive
• Tail Recursion for Fibonacci: Iterative Approach Breakdown
• Improve Your Recursions Performance With Tail Call Optimization (img source)
• 꼬리 재귀 함수란?

Big O

• Introduction to Big O Notation (img source)
• Big O CheatSheet (img source)