JavaScript로 피보나치 수열 효율적으로 구현하기(Dynamic programming)

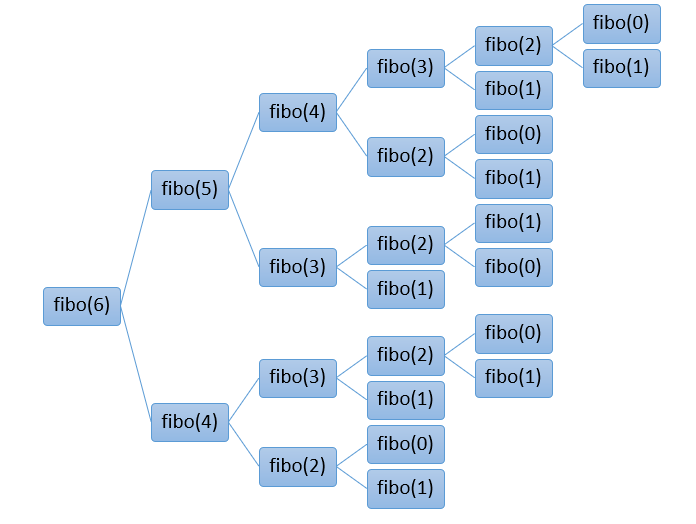
n번째 수는 n-1번째와 n-2번째 수를 합하여 나타내는
피보나치 수열(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...)을 구하는 함수를 구해보았다.

function fibonacci(n) {
  // TODO: 여기에 코드를 작성합니다.

  if(n<=1){
	return n;
  }
 return fibonacci(n-1)+fibonacci(n-2)
}

위와같이 재귀형태로 두 번 함수를 호출하는 형식이다.
이렇게 불필요한 중복호출이 많을 경우 런타임이 길어진다.

어떠한 문제를 풀 때, 작성한 소스가 입력된 값에 대해 문제를 해결하는 데 필요한 시간을 시간복잡도라고 하며, 위의 문제와 같이 풀 경우 이 시간복잡도가 가파르게 증가하게 된다.

n번째 피보나치 항을 여러 번 계산한다고 해서 그 값이 달라지지 않는다. 즉, 한번 구한 항을 기록(memoization) 해 둔 다음, 그 값이 필요할 때 꺼내쓸 수 있다면 굉장히 효율적일 것이다.

동적계획법의 알고리즘은 아래와 같다.
1. 문제를 부분 문제로 나눈다.
2. 가장 작은 문제를 해를 구한 뒤, 테이블에 저장한다.
3. 테이블에 저장되어있는 데이터로 전체의 문제의 해를 구한다.

따라서 재귀함수를 한 번만 호출하는 방식으로 함수를 다르게 작성해볼 수 있다.

function fibonacci(n) {
  // TODO: 여기에 코드를 작성합니다.
 //일단 초기 배열이 [0, 1]에서 시작하여 배열의 요소를 누적해 나가는 방법
 //그리고 이미 구해놓은 것은 배열의 요소로 저장해놓기..!!! 그래야 런타임이 초과되지 않는다

 let newArr = [0, 1]; //0번째 1번째 요소는 고정시켜두고 
 
  let fib = (n) => { //함수 한개를 선언해주고
    if (newArr[n] !== undefined){ 
      return newArr[n]; //이미 있는 건 그대로 리턴
    }
    newArr[n] = fib(n - 1) + fib(n - 2); //없는 건 새로 만들어서 저장!!!*****
    return newArr[n];
  };
  
  return fib(n); 
}

문제를 풀 때 반복문 사용이 금지된다고 하여,,,

• 전달인자 n번째로 배열의 요소가 이미 있는 경우
• 없는 경우: 새로 만들어서 그 값을 배열에 넣어주기(-->피보나치 수열을 '메모'하는 캐시 배열을 만들어서 값을 채워주는 것)

이렇게 간단한 로직으로 나타내어 보았다.

참고자료:
https://velog.io/@polynomeer/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming