
동적 계획법(Dynamic Programming)
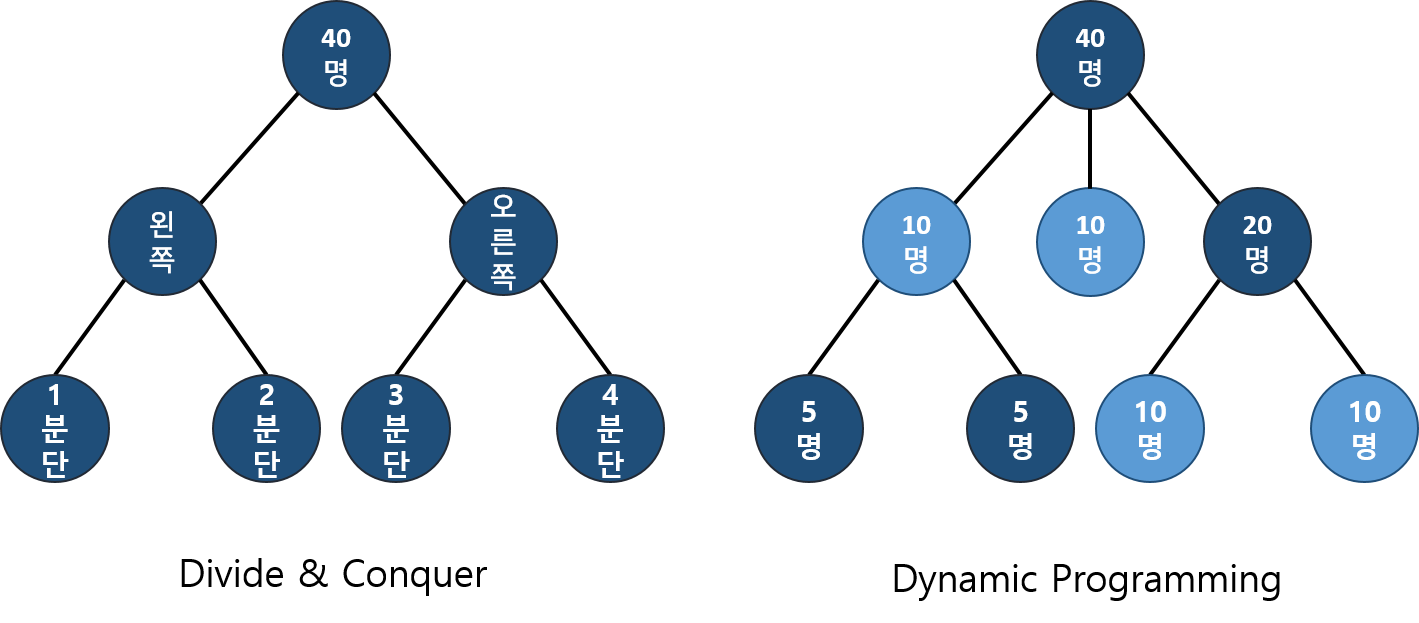
동적 계획법(Dynamic Programming, DP)은 큰 문제를 작은 문제로 나누어서 푸는 방식의 알고리즘이다. 동적 계획법은 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 낸다는 점에서 분할 정복(Divide & Conquer, D&C)과 비슷하다. 하지만 가장 큰 차이점은 동적 계획법에서는 쪼개진 작은 문제가 중복되지만, 분할 정복은 절대로 중복될수가 없다는 점이다.
다시 말하면, 동적 계획법과 분할 정복의 차이는 문제를 나누는 방식이다. 동적 계획법에서는 어떤 부분 문제는 두 개 이상의 문제를 푸는데 사용될 수 있기 때문에, 이 문제의 답을 여러 번 계산하는 대신 한 번만 계산하고 그 결과를 재활용함으로써 속도의 향상을 시킬 수 있다. 이때 이미 계산한 값을 저장해 두는 메모리를 캐시(cache)라고 부르며, 두 번 이상 계산되는 부분 문제를 중복되는 부분 문제(overlapping subproblems)라고 부른다.
1. 동적 계획법의 조건
• 두 가지 속성을 만족해야 동적 계획법으로 문제를 풀 수 있다.
- Overlapping Subproblem : 겹치는 부분(작은) 문제
- Optimal Substructure : 최적 부분구조
1.1. Overlapping Subproblem
겹치는 부분 문제(overlapping subproblem) 는 어떤 문제가 여러개의 부분문제(subproblem)으로 쪼개질 수 있을때 사용하는 용어이다. 이때 '부분 문제'란, 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀 알고리즘을 통해 해결되는 문제를 가리킨다.
대표적인 예로 피보나치 수열이 있다.
0 1 1 2 3 5 8 13 21 34 55 89 ...
- 피보나치 수열은 앞의 두 수를 더한 수가 다음 수가 되는 수열이다.
- F0 = 0
- F1 = 1
- Fn = Fn-1 + Fn-2 (n ≥ 2)
겹치는 부분 문제가 있다면, 큰 문제는 작은 문제들을 통해 정답을 구할 수 있다. 큰 문제는 작은 문제와 같은 방법으로 풀 수 있으며, 모든 문제를 작은 문제로 쪼갤 수 있기 때문이다. (기저 사례를 제외한 모든 문제)
• 문제: N번째 피보나치 수를 구하는 문제
• 작은 문제: N-1번째 피보나치 수를 구하는 문제, N-2번째 피보나치 수를 구하는 문제
• 문제: N-1번째 피보나치 수를 구하는 문제
• 작은 문제: N-2번째 피보나치 수를 구하는 문제, N-3번째 피보나치 수를 구하는 문제
• 문제: N-2번째 피보나치 수를 구하는 문제
• 작은 문제: N-3번째 피보나치 수를 구하는 문제, N-4번째 피보나치 수를 구하는 문제
1.2. Optimal Substructure
최적 부분구조(optimal substructure)는 어떤 문제의 최적의 해결책이 그 부분 문제의 최적의 해결책으로 부터 설계될 수 있는 경우를 말한다. 즉, 최적 부분구조 일때 문제의 정답을 작은 문제의 정답에서 부터 구할 수 있다. 이 속성은 동적 계획법이나 그리디 알고리즘의 유용성을 판별하는데 사용되기도 한다.
(예시)
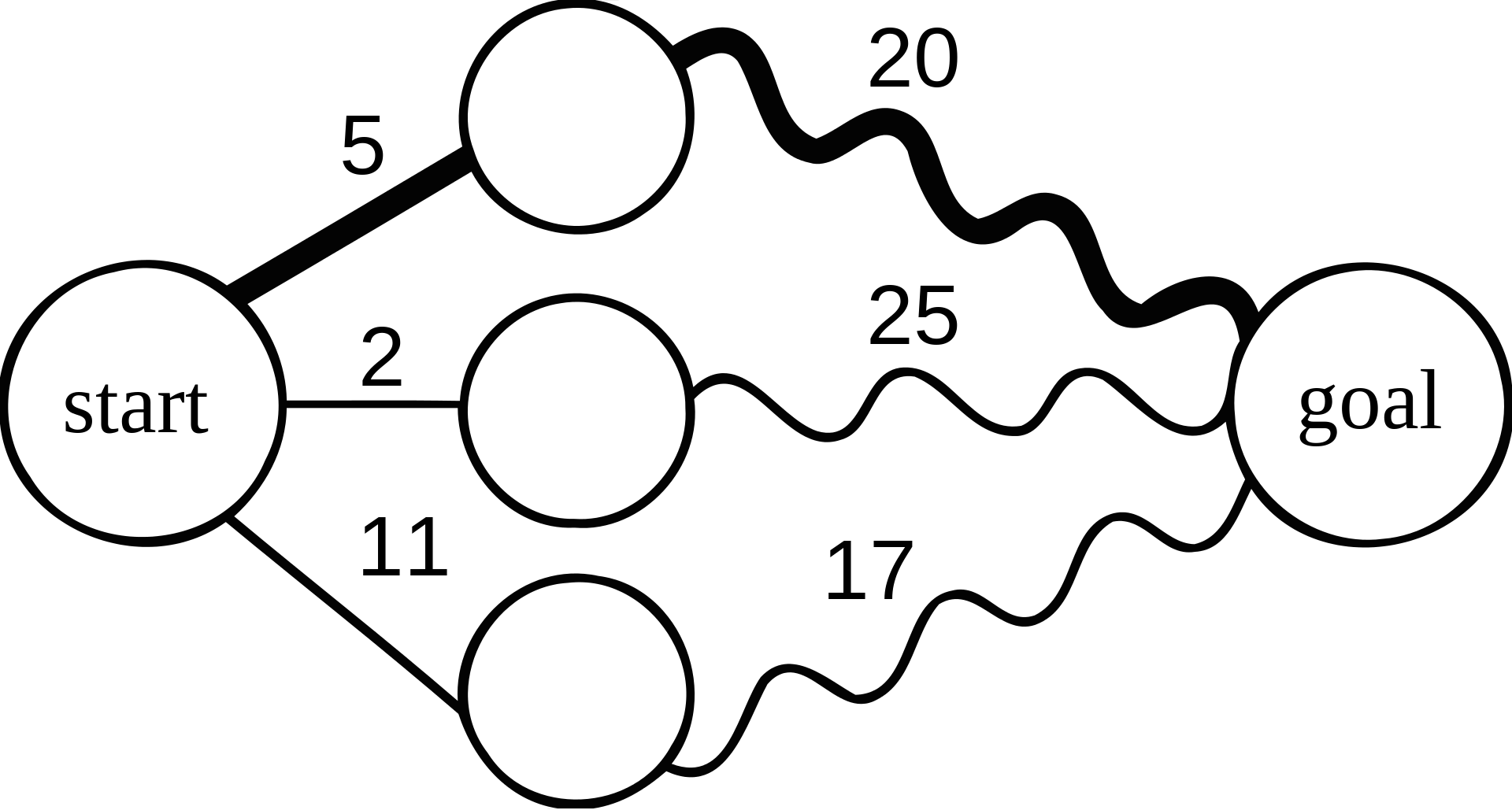
• 서울에서 부산을 가는 가장 빠른 길이 대전과 대구를 순서대로 거쳐야 한다면
• 대전에서 부산을 가는 가장 빠른 길은 대구를 거쳐야 한다.서울->대전->대구->부산 : 가장 빠른 경로
Q) 대전->부산
A) 대전->대구->부산 : 가장 빠른 경로만약 가장 빠른 경로가 서울->대전->울산->부산 이라면
Q) 대전->부산
A) 대전->울산->부산 : 가장 빠른 경로
다시 피보나치 문제로 돌아와보면
• 문제: N번째 피보나치 수를 구하는 문제
• 작은 문제: N-1번째 피보나치 수를 구하는 문제, N-2번째 피보나치 수를 구하는 문제
-> 문제의 정답을 작은 문제의 정답을 합하는 것으로 구할 수 있다.
• 문제: N-1번째 피보나치 수를 구하는 문제
• 작은 문제: N-2번째 피보나치 수를 구하는 문제, N-3번째 피보나치 수를 구하는 문제
-> 문제의 정답을 작은 문제의 정답을 합하는 것으로 구할 수 있다.
• 문제: N-2번째 피보나치 수를 구하는 문제
• 작은 문제: N-3번째 피보나치 수를 구하는 문제, N-4번째 피보나치 수를 구하는 문제
-> 문제의 정답을 작은 문제의 정답을 합하는 것으로 구할 수 있다.
• Optimal Substructure를 만족한다면, 문제의 크기에 상관없이 어떤 한 문제의 정답은
일정하다.
• 10번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
• 9번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
• …
• 5번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
• 4번째 피보나치 수를 구하면서 구한 4번째 피보나치 수
• 4번째 피보나치 수는 항상 같다. -> 겹치는 부분문제의 정답이 항상 같다!
이처럼 같은 값을 매번 구하는 것은 매우 비효율적이다. 이때 이를 해결할 수 있는 방법이 바로 메모이제이션(Memoization)이다.
2. 메모이제이션(Memoization)
동적 계획법에서 각 문제는 한 번만 풀어야 한다. 중복되는 부분 문제를 여러번 풀지 않는다는 뜻이다. Optimal Substructure를 만족하기 때문에 같은 문제는 구할 때마다 정답이 같다. 따라서 정답을 한 번 구했으면 그 정답을 캐시에 메모해놓는다. 이렇게 메모하는 것을 코드의 구현에서는 배열에 저장하는 것으로 할 수 있다. 이를 메모이제이션(Memoization)이라고 한다.
int fibonacci(int n) {
if (n <= 1) { // F(0) = 0, F(1) = 1
return n;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}위의 코드는 피보나치 수를 구하는 함수이다. 점화식을 그대로 표현하여 재귀호출을 하고 있다. F(0)과 F(1)은 더 이상 쪼갤 수 없으므로, 그냥 n을 리턴한다. 이것을 재귀호출 그대로 실행한다면 시간복잡도는 함수의 깊이가 N일때 O(2^N)이다. 이 경우에는 이진트리의 탐색속도와 같다. 다음은 fibonacci(5)를 호출했을때의 그림이다.
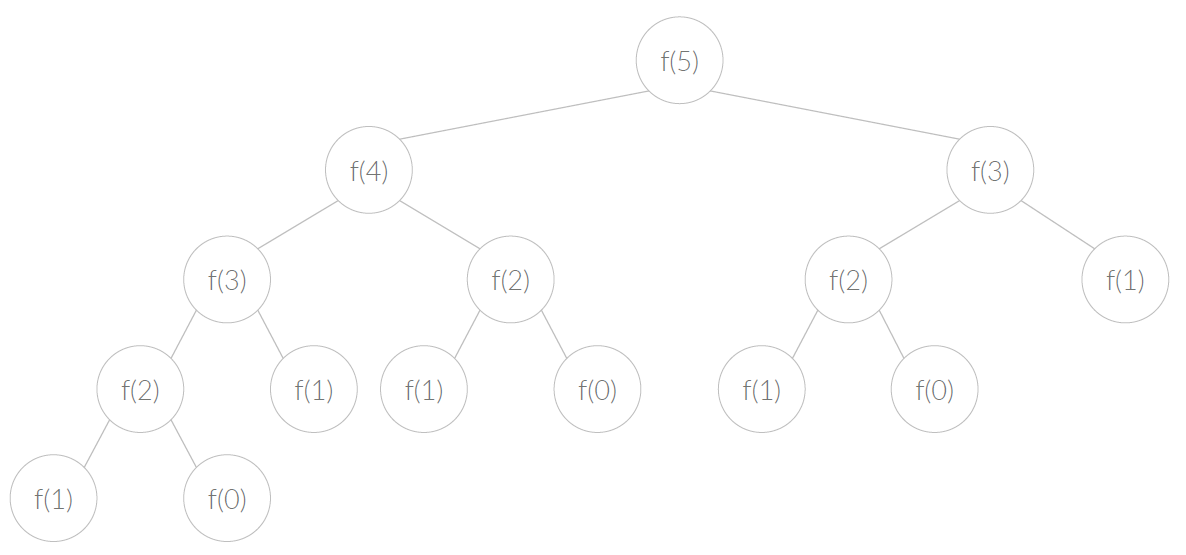
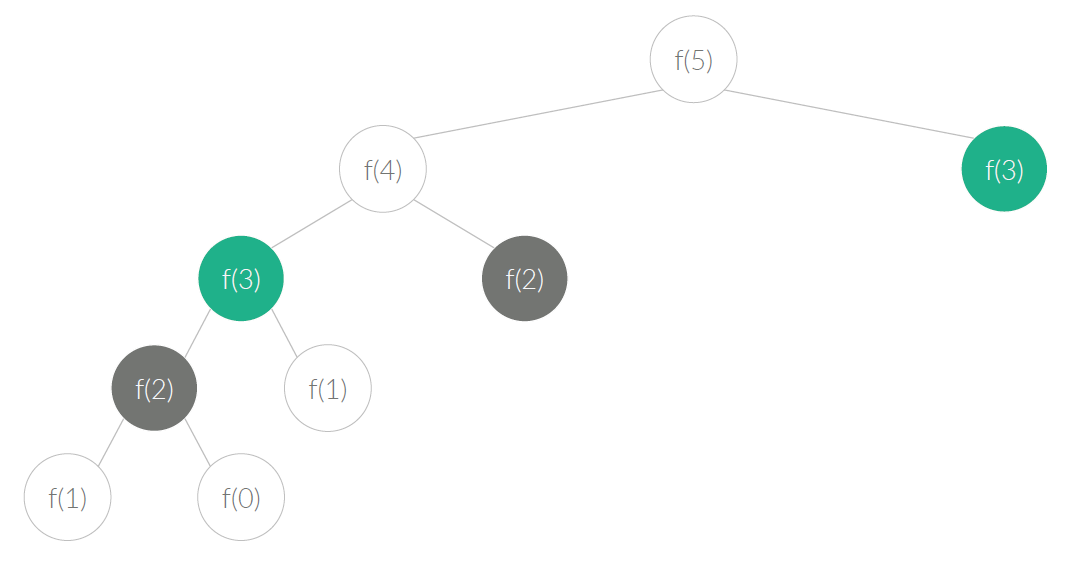
이때 f(3)과 f(2)는 겹치는 부분문제이고 정답이 같으므로, 미리 캐시에 저장해두고 활용할 수 있다. 그래서 메모이제이션하면 부분문제에서 또 파생되는 부분문제의 가지를 모두 생략할 수 있다. (중복되므로) 즉, 모든 문제를 한 번씩만 푼다. 때문에 시간복잡도는 (문제의 개수 x 문제 1개를 푸는시간) 이 되는데, 문제의 개수가 N -> O(N), 문제 1개를 푸는 시간은 +연산 하나(함수의 시간복잡도) -> O(1)이므로, 전체 시간복잡도는 O(N) 이다. 이를 구현한 코드는 다음과 같다.
int memo[100];
int fibonacci(int n) {
if (n <= 1) {
return n;
} else {
memo[n] = fibonacci(n-1) + fibonacci(n-2);
return memo[n];
}
}이런식을 구현하면 될텐데, 여기에서 이미 계산한 부분문제의 경우 그 값을 그대로 사용하는 코드를 추가해야 한다. memo배열에 값이 0이면 답을 구하지 않았다는 뜻이고, 0이 아니면 답을 구한적이 있다(이전의 호출에서 해당 값을 구함)는 뜻이므로, 이를 활용하면 된다.
int memo[100];
int fibonacci(int n) {
if (n <= 1) {
return n;
} else {
if (memo[n] > 0) { // memo의 값이 0이 아니면
return memo[n]; // 그 값을 그대로 사용
}
memo[n] = fibonacci(n-1) + fibonacci(n-2);
return memo[n];
}
}
3. 동적 계획법 구현 방식
동적 계획법의 구현 방식에는 두 가지 방법이 있다.
- Top-down : 큰 문제를 작은 문제로 쪼개면서 푼다. 재귀로 구현
- Bottom-up : 작은 문제부터 차례대로 푼다. 반복문으로 구현
Top-down과 Botton-up의 시간복잡도 차이는 문제에 따라 다를 수 있으므로 정확히 알 수는 없다. Top-down은 재귀호출을 하기때문에 스택의 사용으로 시간이 더 걸릴 것이라고 생각할 수 있겠지만, 실제로 그 차이는 크지 않다. 다만, 파이썬의 경우 재귀 호출 시 스택 오버 플로우(stack overflow)가 발생할 수 있기때문에, Bottom-up으로 구현하는 것이 좋다. C++과 JAVA에서는 재귀로 구현하는 것이 크게 문제가 되지 않는다.
어떠한 상황에서는 오히려 재귀로 구현하는 것이 간단하게 보이는 경우도 있다. 예를 들면, Fn = Fn-10 + Fn-20 이라는 문제가 있다고 하자. 재귀에서 이를 구하려면 F(20)을 호출하면 F(10)+F(0)으로 두번의 호출만에 정답이 구해진다. 하지만 반복문으로 구현하면 F(1),F(2),... 과 같이 반복횟수가 많아진다.
하지만 Top-down으로만 해결가능하거나 Bottom-up으로만 해결가능한 문제는 극히 드문 경우이므로, 아무거나 선택해서 사용하면 된다.
3.1. Top-down
- 큰 문제를 작은 문제로 나눈다.
- 작은 문제를 푼다.
- 작은 문제를 풀었으니, 이제 큰 문제를 푼다.
피보나치 문제로 예를 들면,
- fibonacci(n)라는 문제를 풀기위해서
- 문제를 작은 문제로 나눈다.
• fibonacci(n-1)과 fibonacci(n-2)로 문제를 나눈다. - 작은 문제를 푼다.
• fibonacci(n-1)과 fibonacci(n-2)를 호출해 문제를 푼다. - 작은 문제를 풀었으니, 이제 문제를 푼다.
• fibonacci(n-1)의 값과 fibonacci(n-2)의 값을 더해 문제를 푼다.
코드는 앞에서 설명한것과 같이 재귀호출로 구현할 수 있다.
int d[100];
int fibonacci(int n) {
if (n <= 1) {
return n;
} else {
if (d[n] > 0) { // d의 값이 0이 아니면
return d[n]; // 그 값을 그대로 사용
}
d[n] = fibonacci(n-1) + fibonacci(n-2);
return d[n];
}
}3.2. Bottom-up
- 문제를 크기가 작은 문제부터 차례대로 푼다.
- 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
- 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
- 반복하다 보면 가장 큰 문제를 풀 수 있다.
똑같이 피보나치 문제로 예를 들면,
- 문제를 크기가 작은 문제부터 차례대로 푼다.
• for (int i=2; i<=n; i++) - 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
• for (int i=2; i<=n; i++) - 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
• d[i] = d[i-1] + d[i-2]; - 반복하다 보면 가장 큰 문제를 풀 수 있다.
• d[n]을 구하게 된다.
따라서 다음과 같이 반복문으로 코드를 작성할 수 있다.
int d[100];
int fibonacci(int n) {
d[0] = 0;
d[1] = 1;
for (int i=2; i<=n; i++) { // 2에서 부터 시작해서 n까지 반복
d[i] = d[i-1] + d[i-2];
}
return d[n];
}4. 동적 계획법을 통한 문제풀이
- 먼저, 문제에서 구하려고 하는 답을 문장으로 나타낸다.
- (예: 피보나치 수를 구하는 문제 -> N번째 피보나치 수)
- 이제 그 문장에 나와있는 변수의 개수만큼 메모하는 캐시 배열을 만든다.
- Top-down인 경우에는 재귀 호출의 인자의 개수가 된다.
- 마지막으로, 문제를 작은 문제로 나누고, 수식(점화식)을 이용해서 문제를 표현해야 한다.


동적계획법은 bottom up 이어야 한다고 생각했는데 그런 게 아니었군요